目录

一、基本概念

二、EM算法详解

三、高斯混合模型（GMM）的算法步骤及Python代码的完整实现

四、总结

---

一、基本概念

EM算法（无监督学习算法）是一种迭代优化算法，用于含有隐变量的概率模型的参数估计。

基本思路

1.当模型包含观测变量和隐变量时

2.直接最大化观测数据的似然函数很困难

3.EM算法通过迭代的方式间接求解

二、EM算法详解

EM算法似然函数：

给定的m个训练样本{x(1),x(2),...,x(m)}，样本间独立，找出样本的模型参数θ，极大 化模型分布的对数似然函数如下：

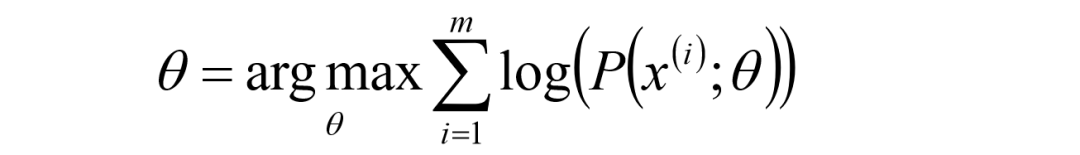
假定样本数据中存在隐含数据z={z(1),z(2),...,z(k)}，此时极大化模型分布的对数似然函数如下：

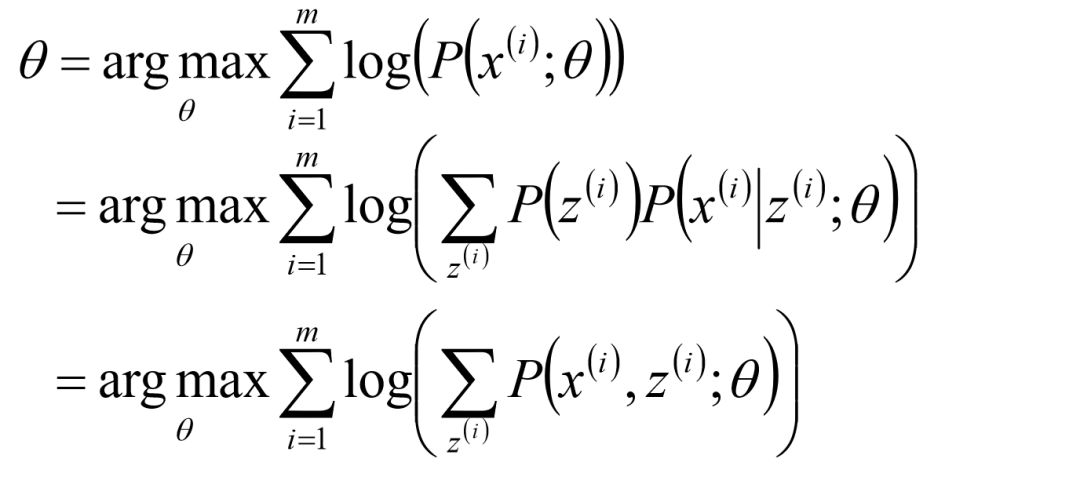
进一步地：利用Jensen不等式的性质

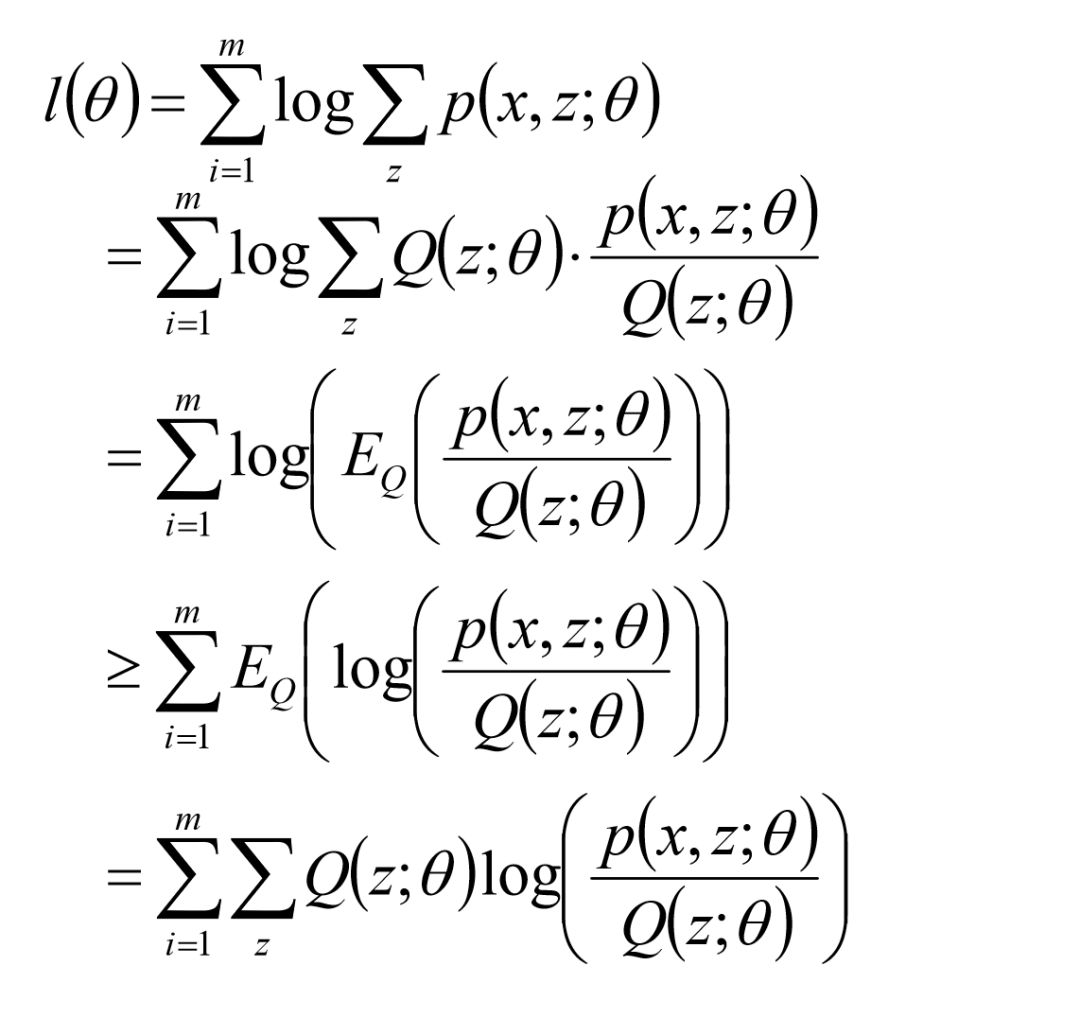
其中，Jensen不等式为，当函数f是凸函数时，

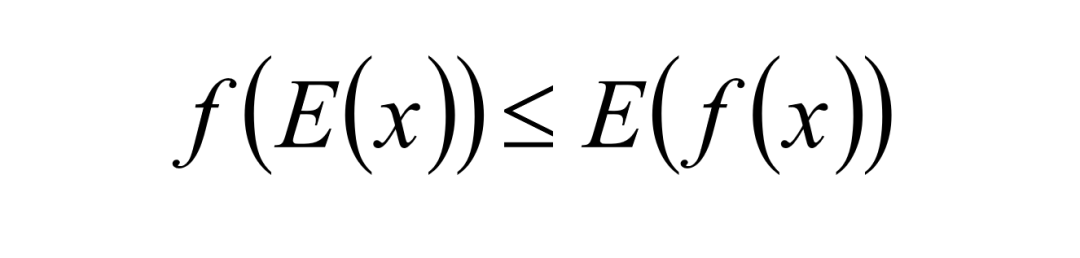
最终的优化目标为：

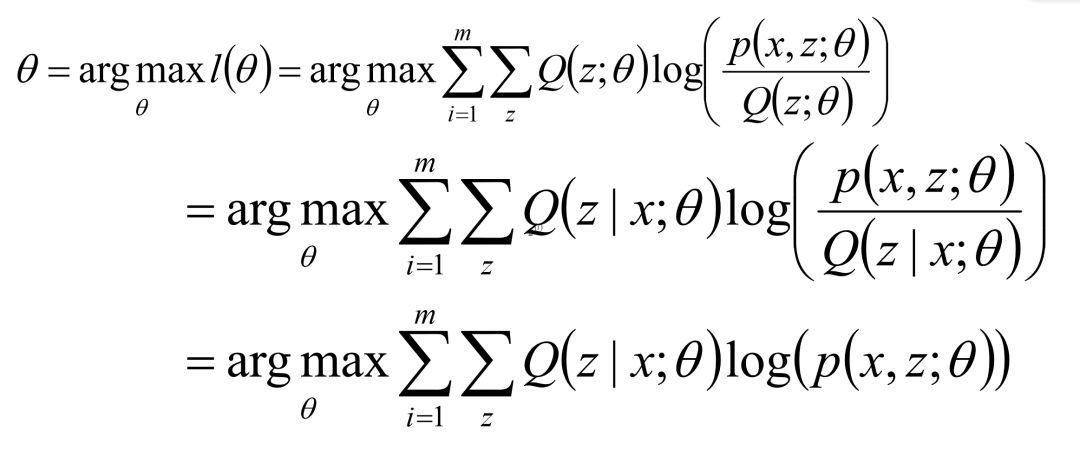
高斯混合模型（GMM）中的EM算法实现

GMM模型由多个高斯模型线性叠加混合而成：

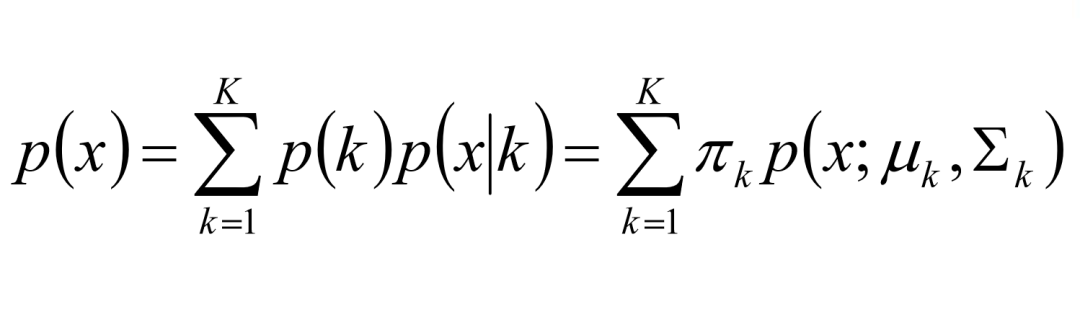
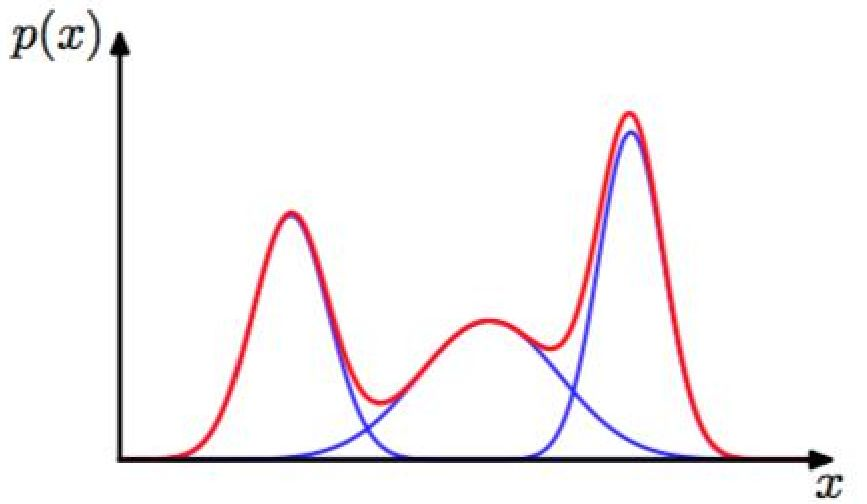
特别地，GMM模型用于聚类任务中，就有了高斯混合聚类模型。

E步骤（期望）

def E_step(self, X):
    # 计算每个样本属于每个高斯分布的后验概率
    responsibilities = np.zeros((X.shape[0], self.k))
    for i in range(self.k):
        log_prob = self.log_gaussian_prob(X, self.means[i], self.covs[i])
        responsibilities[:, i] = np.log(self.phi[i]) + log_prob
    
    # 归一化
    log_sum = logsumexp(responsibilities, axis=1)
    responsibilities = np.exp(responsibilities - log_sum[:, np.newaxis])
    
    return responsibilities

M步骤（最大化）

def M_step(self, X, responsibilities):
    # 更新权重
    self.phi = responsibilities.sum(axis=0) / X.shape[0]
    
    # 更新均值
    for i in range(self.k):
        self.means[i] = np.sum(responsibilities[:, i, np.newaxis] * X, axis=0) / (X.shape[0] * self.phi[i])
        
        # 更新协方差
        diff = X - self.means[i]
        weighted_diff = responsibilities[:, i, np.newaxis] * diff
        self.covs[i] = weighted_diff.T @ diff / (X.shape[0] * self.phi[i])
        
        # 保证协方差矩阵正定
        self.covs[i] += np.eye(X.shape[1]) * 1e-6

算法收敛判断

对数似然收敛

def check_convergence(self, old_ll, new_ll):
    return np.abs(new_ll - old_ll) < self.eps

EM算法的优缺点

优点

1.可处理含隐变量的复杂模型

2.迭代求解，适用于多种概率模型

3.保证似然函数单调递增

缺点

1.收敛到局部最优

2.对初始值敏感

3.计算复杂度较高

EM算法的应用

EM算法广泛应用于聚类分析，缺失数据处理，图像去噪，推荐系统，生物信息学，金融和社交网络分析等领域。

三、高斯混合模型（GMM）的算法步骤及Python代码的完整实现

（一）算法步骤

模型初始化 (`_random_init_params` 和 `_kmeans_init_params`)

随机初始化：

  1. 随机生成权重 (Dirichlet分布)

  2. 从数据中随机选择均值点

  3. 使用数据协方差矩阵初始化

K-means初始化：

  1. 使用K-means聚类结果确定初始均值

  2. 计算每个簇的权重和协方差

对数高斯概率计算 (`log_gaussian_prob`)

使用对数空间计算，提高数值稳定性

计算马氏距离

使用 `slogdet` 计算行列式的对数

EM迭代 (`EM_fit`)

1. 初始化参数

2. E步骤：计算后验概率

   使用 `logsumexp` 避免数值下溢

3. M步骤：更新模型参数

4. 计算对数似然

5. 计算模型选择指标 (BIC, AIC)

6. 检查收敛

模型评估 (`model_evaluation`)

使用多个指标评估聚类性能：

1.轮廓系数

2.卡林斯基-哈拉巴兹指数

3.戴维斯-布尔丁指数

GUI界面设计

1. 数据加载与预处理

支持CSV和NumPy文件

可选数据标准化

处理一维和多维数据

2. 模型参数选择

高斯分布数量

初始化方法

执行分析

3.可视化

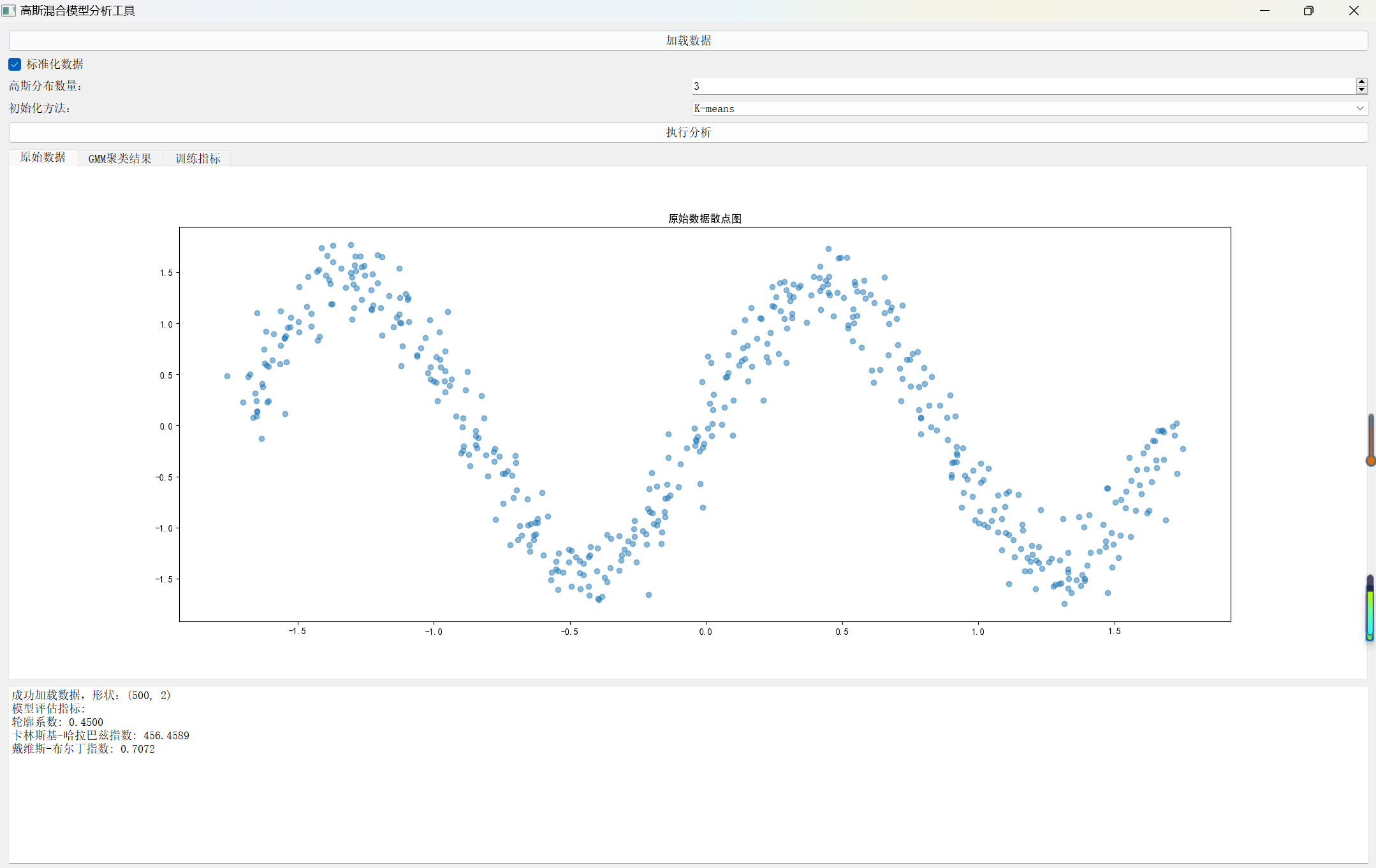
原始数据展示

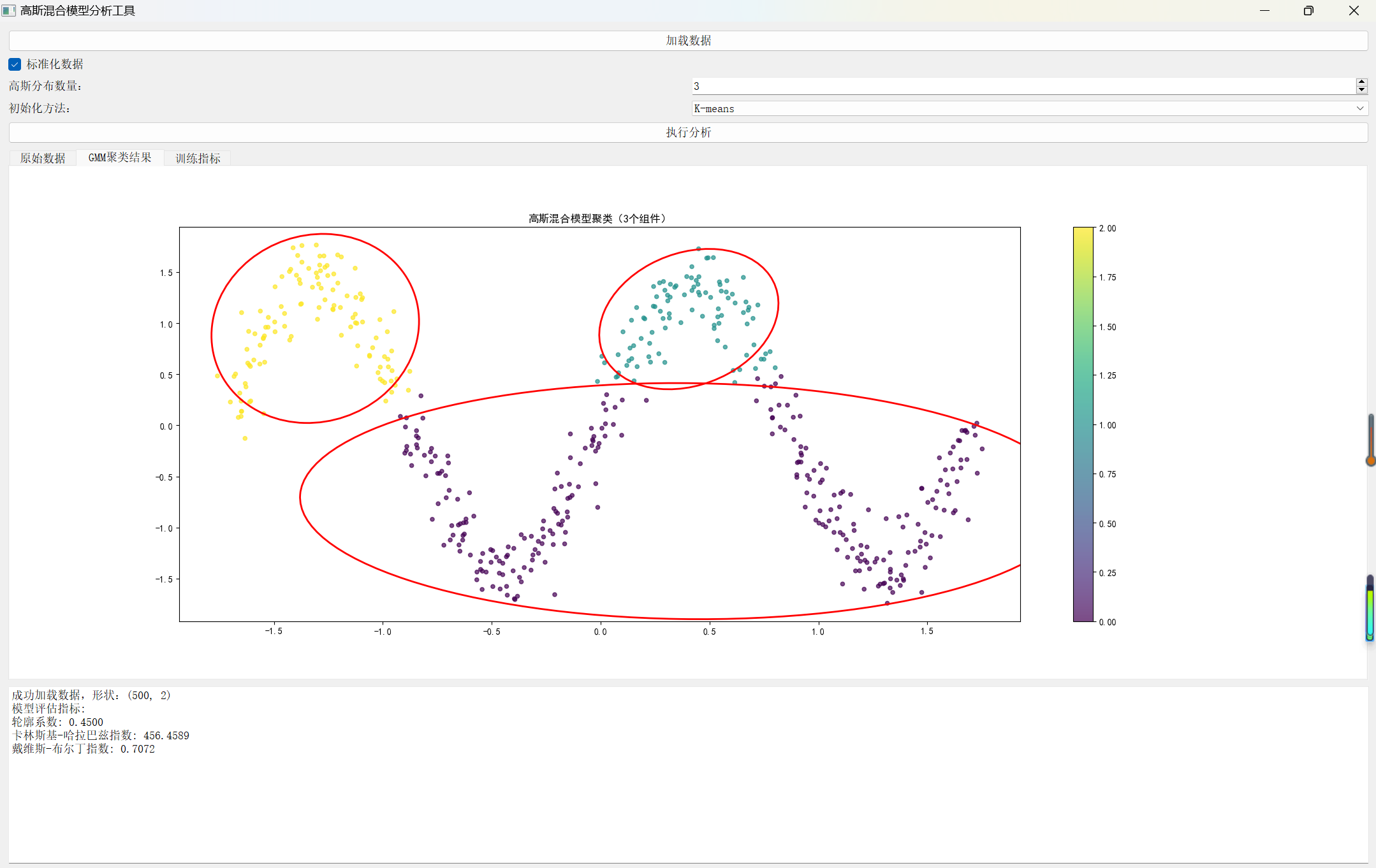
聚类结果

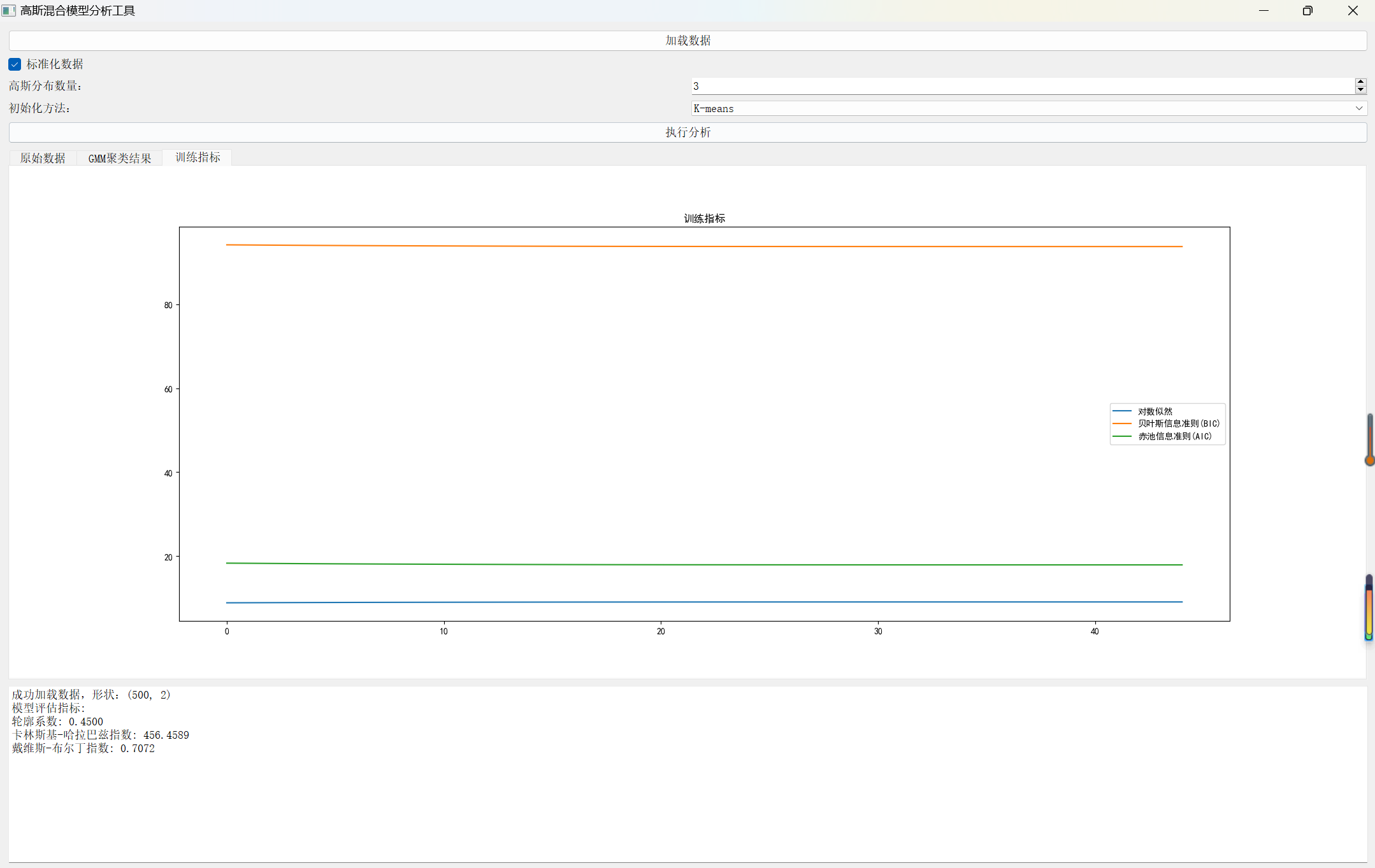
训练过程指标

（二）Python代码的完整实现

1.先运行生成随机数据集的代码

import numpy as np
import pandas as pd


def generate_sin_data(n_samples=500, noise=0.15):
    """
    生成一个带有噪声的正弦曲线形状的二维数据集。

    参数:
    n_samples (int): 生成的样本点数量。
    noise (float): 添加到数据中的高斯噪声的标准差。

    返回:
    numpy.ndarray: 形状为 (n_samples, 2) 的数据集。
    """
    # 沿x轴在[-2*pi, 2*pi]范围内均匀生成点
    x = np.linspace(-2 * np.pi, 2 * np.pi, n_samples)

    # 计算对应的正弦值
    y = np.sin(x)

    # 将x和y合并成一个 (n_samples, 2) 的数组
    # 并为每个点的x和y坐标添加高斯噪声
    X = np.vstack((x, y)).T
    X += np.random.normal(scale=noise, size=X.shape)

    return X


# --- 主程序 ---
if __name__ == "__main__":
    # 设置随机种子以保证结果可复现
    np.random.seed(0)

    # 生成数据集
    num_points = 500
    data_noise = 0.15
    sindata = generate_sin_data(n_samples=num_points, noise=data_noise)

    # 将数据保存到 CSV 文件，不包含表头和索引
    # 这与 np.loadtxt('sindata.csv', delimiter=',') 的读取方式完全匹配
    pd.DataFrame(sindata).to_csv('sindata.csv', header=False, index=False)

    print(f"成功生成 {num_points} 个样本点，并保存到 'sindata.csv' 文件中。")
    print("数据集预览 (前5行):")
    print(sindata[:5])

2.再运行高斯混合模型（GMM）的代码

import os
import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.cluster import KMeans
from scipy.special import logsumexp
from sklearn.metrics import (
    silhouette_score,
    calinski_harabasz_score,
    davies_bouldin_score,
    adjusted_rand_score
)
from sklearn.preprocessing import StandardScaler
import warnings
import seaborn as sns
import pandas as pd

# 设置中文字体支持
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

# GUI相关库
from PyQt5.QtWidgets import (
    QApplication, QMainWindow, QVBoxLayout, QHBoxLayout,
    QLabel, QPushButton, QFileDialog, QTextEdit, QTabWidget,
    QWidget, QComboBox, QSpinBox, QMessageBox, QCheckBox
)
from PyQt5.QtCore import Qt
from matplotlib.backends.backend_qt5agg import FigureCanvasQTAgg as FigureCanvas
from matplotlib.figure import Figure

# 抑制警告
warnings.filterwarnings("ignore")


class GMM:
    def __init__(self, n_components=2, eps=1e-4, max_iter=100, init='kmeans', random_state=42):
        """
        高斯混合模型（Gaussian Mixture Model）增强实现

        参数:
        - n_components: 高斯分布的数量
        - eps: 迭代收敛阈值
        - max_iter: 最大迭代次数
        - init: 初始化方法 ('random' 或 'kmeans')
        - random_state: 随机数种子
        """
        self.k = n_components
        self.eps = eps
        self.max_iter = max_iter
        self.init = init
        self.random_state = random_state
        np.random.seed(random_state)

        self.phi = None  # 每个高斯分布的权重
        self.means = None  # 每个高斯分布的均值
        self.covs = None  # 每个高斯分布的协方差矩阵

        # 存储训练过程的指标
        self.log_likelihoods = []
        self.bic_scores = []
        self.aic_scores = []
        self.labels_ = None  # 存储聚类标签

    def log_gaussian_prob(self, x, mu, sigma):
        """计算多元高斯分布的对数概率密度"""
        d = x.shape[-1]
        try:
            sign, logdet = np.linalg.slogdet(sigma)
            inv_sigma = np.linalg.inv(sigma)

            diff = x - mu
            mahalanobis = np.sum(diff @ inv_sigma * diff, axis=-1)

            log_prob = -0.5 * (d * np.log(2 * np.pi) + logdet + mahalanobis)
            return log_prob
        except np.linalg.LinAlgError:
            return np.full(x.shape[0], -np.inf)

    def EM_fit(self, X):
        """使用EM算法拟合GMM模型"""
        # 参数初始化
        if self.init == 'random':
            self._random_init_params(X)
        elif self.init == 'kmeans':
            self._kmeans_init_params(X)
        else:
            raise ValueError("初始化方法必须是 'random' 或 'kmeans'")

        n, d = X.shape
        qz = np.zeros((n, self.k))

        # 迭代优化
        for t in range(self.max_iter):
            # E步骤：计算后验概率
            for i in range(self.k):
                log_prob = self.log_gaussian_prob(X, self.means[i], self.covs[i])
                qz[:, i] = np.log(self.phi[i]) + log_prob

            log_sum = logsumexp(qz, axis=1)
            qz = np.exp(qz - log_sum[:, np.newaxis])

            # M步骤：更新模型参数
            self.phi = qz.sum(axis=0) / n

            for i in range(self.k):
                self.means[i] = np.sum(qz[:, i, np.newaxis] * X, axis=0) / (n * self.phi[i])

                diff = X - self.means[i]
                weighted_diff = qz[:, i, np.newaxis] * diff
                self.covs[i] = weighted_diff.T @ diff / (n * self.phi[i])

                self.covs[i] += np.eye(d) * 1e-6

            # 计算对数似然
            ll = self._calc_log_likelihood(X)
            self.log_likelihoods.append(ll)

            # 计算BIC和AIC
            num_params = self.k * (d + d * (d + 1) / 2 + 1)
            self.bic_scores.append(-2 * ll + num_params * np.log(n))
            self.aic_scores.append(-2 * ll + 2 * num_params)

            # 检查收敛
            if t > 0 and np.abs(self.log_likelihoods[-1] - self.log_likelihoods[-2]) < self.eps:
                break

        # 存储最终的聚类标签
        self.labels_ = self.predict(X)
        return self

    def _calc_log_likelihood(self, X):
        """计算总对数似然"""
        ll = 0
        for i in range(self.k):
            log_prob = self.log_gaussian_prob(X, self.means[i], self.covs[i])
            ll += np.sum(logsumexp(log_prob + np.log(self.phi[i])))
        return ll

    def _random_init_params(self, X):
        """随机初始化模型参数"""
        n, d = X.shape
        self.phi = np.random.dirichlet(np.ones(self.k))

        indices = np.random.choice(n, self.k, replace=False)
        self.means = X[indices]

        base_cov = np.cov(X.T)
        self.covs = np.array([base_cov + np.eye(d) * 0.1 for _ in range(self.k)])

    def _kmeans_init_params(self, X):
        """使用K-means初始化模型参数"""
        kmeans = KMeans(n_clusters=self.k, random_state=self.random_state).fit(X)

        self.phi = np.bincount(kmeans.labels_, minlength=self.k) / len(X)

        self.means = np.zeros((self.k, X.shape[1]))
        self.covs = np.zeros((self.k, X.shape[1], X.shape[1]))

        for i in range(self.k):
            X_i = X[kmeans.labels_ == i]
            if len(X_i) > 0:
                self.means[i] = X_i.mean(axis=0)

                cov = np.cov(X_i.T)
                self.covs[i] = cov + np.eye(X.shape[1]) * 1e-6
            else:
                self.means[i] = X.mean(axis=0)
                self.covs[i] = np.cov(X.T) + np.eye(X.shape[1]) * 1e-6

    def predict(self, X):
        """预测样本属于哪个高斯分布"""
        responsibilities = np.zeros((X.shape[0], self.k))
        for i in range(self.k):
            responsibilities[:, i] = self.phi[i] * np.exp(
                self.log_gaussian_prob(X, self.means[i], self.covs[i])
            )
        return np.argmax(responsibilities, axis=1)


def model_evaluation(X, labels_true, labels_pred):
    """
    模型评估函数，计算多个指标

    参数:
    - X: 数据集
    - labels_true: 真实标签（如果有）
    - labels_pred: 预测标签

    返回:
    - 评估指标字典
    """
    metrics = {
        '轮廓系数': silhouette_score(X, labels_pred),
        '卡林斯基-哈拉巴兹指数': calinski_harabasz_score(X, labels_pred),
        '戴维斯-布尔丁指数': davies_bouldin_score(X, labels_pred)
    }

    # 如果有真实标签，计算调整兰德指数
    if labels_true is not None:
        metrics['调整兰德指数'] = adjusted_rand_score(labels_true, labels_pred)

    return metrics


def plot_gmm_results(X, gmm, ax=None):
    """绘制GMM聚类结果"""
    if ax is None:
        fig, ax = plt.subplots(figsize=(10, 6))

    labels = gmm.predict(X)
    scatter = ax.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', alpha=0.7, s=20)

    for i in range(gmm.k):
        cov = gmm.covs[i][:2, :2]
        eigenvalues, eigenvectors = np.linalg.eigh(cov)

        angle = np.degrees(np.arctan2(eigenvectors[1, 0], eigenvectors[0, 0]))
        width, height = 4 * np.sqrt(eigenvalues)

        ellipse = mpl.patches.Ellipse(
            gmm.means[i, :2],
            width, height,
            angle=angle,
            fill=False,
            edgecolor='red',
            linewidth=2
        )
        ax.add_artist(ellipse)

    ax.set_title(f'高斯混合模型聚类（{gmm.k}个组件）')
    plt.colorbar(scatter, ax=ax)
    return ax


class GMMAnalysisApp(QMainWindow):
    def __init__(self):
        super().__init__()
        self.setWindowTitle('高斯混合模型分析工具')
        self.setGeometry(100, 100, 1400, 900)

        # 主布局
        main_widget = QWidget()
        main_layout = QVBoxLayout()
        main_widget.setLayout(main_layout)
        self.setCentralWidget(main_widget)

        # 数据加载区域
        data_layout = QHBoxLayout()
        load_btn = QPushButton('加载数据')
        load_btn.clicked.connect(self.load_data)
        data_layout.addWidget(load_btn)

        # 数据预处理选项
        preprocess_layout = QHBoxLayout()
        self.standardize_checkbox = QCheckBox('标准化数据')
        self.standardize_checkbox.setChecked(True)
        preprocess_layout.addWidget(self.standardize_checkbox)

        # 组件数选择
        components_layout = QHBoxLayout()
        components_label = QLabel('高斯分布数量：')
        self.components_spinbox = QSpinBox()
        self.components_spinbox.setRange(2, 10)
        self.components_spinbox.setValue(3)
        components_layout.addWidget(components_label)
        components_layout.addWidget(self.components_spinbox)

        # 初始化方法选择
        init_layout = QHBoxLayout()
        init_label = QLabel('初始化方法：')
        self.init_combo = QComboBox()
        self.init_combo.addItems(['K-means', '随机'])
        init_layout.addWidget(init_label)
        init_layout.addWidget(self.init_combo)

        # 分析按钮
        analyze_btn = QPushButton('执行分析')
        analyze_btn.clicked.connect(self.perform_analysis)

        # 结果显示区域
        self.result_text = QTextEdit()
        self.result_text.setReadOnly(True)

        # 选项卡
        self.tab_widget = QTabWidget()

        # 添加到主布局
        main_layout.addLayout(data_layout)
        main_layout.addLayout(preprocess_layout)
        main_layout.addLayout(components_layout)
        main_layout.addLayout(init_layout)
        main_layout.addWidget(analyze_btn)
        main_layout.addWidget(self.tab_widget)
        main_layout.addWidget(self.result_text)

        # 数据和模型
        self.X = None
        self.gmm = None
        self.scaler = StandardScaler()

    def load_data(self):
        """加载数据文件"""
        filename, _ = QFileDialog.getOpenFileName(self, '选择数据文件', '', 'CSV文件 (*.csv);;NumPy文件 (*.npy)')
        if filename:
            try:
                if filename.endswith('.csv'):
                    self.X = np.loadtxt(filename, delimiter=',')
                else:
                    self.X = np.load(filename)

                # 检查数据维度
                if self.X.ndim == 1:
                    self.X = self.X.reshape(-1, 1)

                self.result_text.append(f'成功加载数据，形状：{self.X.shape}')
            except Exception as e:
                QMessageBox.warning(self, '错误', f'加载数据失败：{str(e)}')

    def perform_analysis(self):
        """执行GMM分析"""
        if self.X is None:
            QMessageBox.warning(self, '警告', '请先加载数据')
            return

        # 清空之前的选项卡
        while self.tab_widget.count():
            self.tab_widget.removeTab(0)

        # 数据预处理
        X_processed = self.X.copy()
        if self.standardize_checkbox.isChecked():
            X_processed = self.scaler.fit_transform(X_processed)

        # 获取参数
        n_components = self.components_spinbox.value()
        init_method = '随机' if self.init_combo.currentText() == '随机' else 'kmeans'

        # 训练GMM
        self.gmm = GMM(n_components=n_components, init=init_method)
        self.gmm.EM_fit(X_processed)

        # 模型评估
        metrics = model_evaluation(X_processed, None, self.gmm.labels_)

        # 显示评估结果
        metrics_text = "模型评估指标:\n" + "\n".join([f"{k}: {v:.4f}" for k, v in metrics.items()])
        self.result_text.append(metrics_text)

        # 创建可视化选项卡
        self.create_visualization_tabs(X_processed)

    def create_visualization_tabs(self, X_processed):
        """创建可视化选项卡"""
        # 原始数据散点图
        fig1 = Figure(figsize=(10, 6))
        canvas1 = FigureCanvas(fig1)
        ax1 = fig1.add_subplot(111)

        # 如果数据是一维的，使用直方图
        if X_processed.shape[1] == 1:
            ax1.hist(X_processed, bins='auto', alpha=0.7)
            ax1.set_title('原始数据直方图')
        else:
            ax1.scatter(X_processed[:, 0], X_processed[:, 1], alpha=0.5)
            ax1.set_title('原始数据散点图')

        self.tab_widget.addTab(canvas1, '原始数据')

        # GMM聚类结果
        fig2 = Figure(figsize=(10, 6))
        canvas2 = FigureCanvas(fig2)

        # 如果数据是一维的，使用不同的可视化方法
        if X_processed.shape[1] == 1:
            ax2 = fig2.add_subplot(111)
            for i in range(self.gmm.k):
                # 绘制每个高斯分布的概率密度
                x = np.linspace(X_processed.min(), X_processed.max(), 100)
                pdf = self.gmm.phi[i] * np.exp(
                    -0.5 * ((x - self.gmm.means[i, 0]) / np.sqrt(self.gmm.covs[i, 0, 0])) ** 2) / np.sqrt(
                    2 * np.pi * self.gmm.covs[i, 0, 0])
                ax2.plot(x, pdf, label=f'组件 {i + 1}')
            ax2.set_title('高斯混合模型概率密度')
            ax2.legend()
        else:
            ax2 = fig2.add_subplot(111)
            plot_gmm_results(X_processed, self.gmm, ax2)

        self.tab_widget.addTab(canvas2, 'GMM聚类结果')

        # 训练过程指标
        fig3 = Figure(figsize=(10, 6))
        canvas3 = FigureCanvas(fig3)
        ax3 = fig3.add_subplot(111)
        ax3.plot(self.gmm.log_likelihoods, label='对数似然')
        ax3.plot(self.gmm.bic_scores, label='贝叶斯信息准则(BIC)')
        ax3.plot(self.gmm.aic_scores, label='赤池信息准则(AIC)')
        ax3.set_title('训练指标')
        ax3.legend()
        self.tab_widget.addTab(canvas3, '训练指标')


def main():
    app = QApplication(sys.argv)
    gmm_app = GMMAnalysisApp()
    gmm_app.show()
    sys.exit(app.exec_())


if __name__ == '__main__':
    main()

程序运行结果如下：

随机生成数据集的运行结果部分截图：

高斯混合模型（GMM）的程序运行结果如下：

四、总结

本文详细介绍了EM算法及其在高斯混合模型(GMM)中的应用。EM算法是一种迭代优化方法，适用于含有隐变量的概率模型参数估计。文章解析了EM算法的理论基础，包括E步骤(期望)和M步骤(最大化)的实现细节，并重点阐述了GMM模型的参数初始化、对数似然计算和收敛判断方法。通过Python代码实现了包含K-means和随机两种初始化方式的GMM模型，提供了完整的GUI界面支持数据加载、参数设置和可视化分析。实验结果表明，该方法能有效处理聚类任务，并可通过轮廓系数等指标评估模型性能。EM算法虽存在局部最优等局限，但在处理复杂概率模型方面具有显著优势。