NSGA-II（带精英策略的非支配排序的多目标遗传算法）：原理讲解与代码实现 Matlab代码免费获取

今天给大家带来一期带精英策略的非支配排序的遗传算法(NSGA-II)的原理介绍，并附带Matlab代码实现！本期代码免费赠送，需要代码的小伙伴可直接拉到最后！

强盛机器学习

4894人浏览 · 2024-08-20 23:08:56

强盛机器学习 · 2024-08-20 23:08:56 发布

声明：文章是从本人公众号中复制而来，因此，想最新最快了解各类智能优化算法及其改进的朋友，可关注我的公众号：强盛机器学习，不定期会有很多免费代码分享~

今天给大家带来一期带精英策略的非支配排序的遗传算法(NSGA-II)的原理介绍，并附带Matlab代码实现！

NSGA-II（Non-dominated Sorting Genetic Algorithm II）是一种多目标优化算法，用于解决具有多个冲突目标的优化问题。该算法由Deb等人在2002年提出。相遇比早期版本的NSGA算法，NSGA-II主要克服了计算复杂度高、缺乏精英主义以及需要用户定义共享参数等缺点，主要包括以下三个方面的改进：

1)提出了快速非支配的排序算法，降低了计算非支配序的复杂度。

2)引入了精英策略，扩大了采样空间。

3)引入拥挤度和拥挤度比较算子，从而保证了种群的多样性。

以下会一一介绍这三点，本期代码免费赠送，需要代码的小伙伴可直接拉到最后！

什么是非支配集合

以最小化为例，解A对解B在某个目标函数上存在f(A)<f(B)，则称解A支配解B。在解集内，找不到其他解在所有目标函数上都优于解A的解，则解A为Pareto最优解，这一类解组成的集合为非支配集合或Pareto最优解集。

当出现大量满足支配与非支配的个体时，会出现一种如下的分层现象。因为优化问题，通常存在一个解集，这些解之间就全体目标函数而言是无法比较优劣的，以下图片清晰的描述了这一现象：

如何进行快速非支配排序

在种群中，每个个体i都有两个参数：ni和Si。其中，ni代表支配个体i的解的个体数量，而Si则是被个体i支配的解的个体集合。

1）首先，找出种群中所有n=0的个体，并将它们存入当前非支配集合Z1中；

2）接着，对于当前非支配集合Z1中的每个个体j，遍历它所支配的个体集合 Sj，将集合Sj中每个个体t的nt 减去1，即支配个体t的个体数量减少1（因为支配个体tt的个i已经被存入当前非支配集Z1中）。如果此时nt−1=0，则将个体t存入另一个集合HH；

3）将Z1作为第一级非支配个体的集合。这个集合中的解是最优的，它们只支配其他个体，而不受任何其他个体的支配。为该集合内的所有个体赋予相同的非支配序列（rank）。然后，继续对集合进行上述分级操作，并赋予相应的非支配序列，直到所有个体都被分级，且都获得了相应的非支配序列。

每次迭代操作，即上述快速非支配排序算法的步骤1)和2)需要进行N 次计算。因此，整个迭代过程的计算复杂度最大为N2。因此，整个快速非支配排序算法的计算复杂度为：max(mN2,N2)=mN2。

如何引入拥挤度与拥挤度比较算子

一、拥挤度的确定

在NSGA-II算法中，引入了拥挤度的概念。拥挤度用来表示种群中某个特定点周围个体的密集程度，通常用idid表示。拥挤度可以通过衡量围绕个体i的最大长方形的长度来表示，这个长方形包含个体ii，但不包含其他个体。具体如下图所示：

因此，拥挤度的计算步骤如下：

首先，每个点的拥挤度i置为0；其次，针对每个优化目标，对种群进行非支配排序，令边界上的两个个体的拥挤度为无穷大，即od=ld=∞；最后，对种群中其他个体的拥挤度进行计算：

在上式中，id表示i点的拥挤度，f(i+1)j表示i+1点第j个目标函数的函数值，f(i-1)j表示i-1点的第j个目标函数的函数值。

二、拥挤度比较算子

经过前面的快速非支配排序以及拥挤度计算之后，种群中的每个个体i都拥有如下两个属性：①非支配排序决定的非支配序(ranki)。②拥挤度(id)。因此，可以定义拥挤度比较算子：个体i与另一个个体j进行比较，只要下面任意一个条件成立，则个体i获胜：

①若个体i所处的非支配层优于个体j所处的非支配层，即ranki<rankj。

②若种群中两个个体有相同的等级(处在相同的非支配层)，且个体i的拥挤距离大于个体j的拥挤距离，即ranki=rankj，且id>jd。

条件1用来确保被选择的个体属于在种群中比较优秀的非劣等级。条件2是根据它们的拥挤距离来选择处在相同的非支配层的两个个体，位于较不拥挤区域的个体(有较大的拥挤度)会被选择。根据这两个条件，选出种群中胜出的个体进入下一个操作。

如何引入精英策略

NSGA-II算法采用了精英策略，以防止在种群进化过程中优质个体的丢失。该策略通过将父代种群与其生成的子代种群混合，并对其进行非支配排序，从而有效地保留父代种群中的优秀个体。精英策略的具体执行步骤如下图所示：

首先，将第t代产生的子代种群Qt与父代种群Pt合并在一起，组成种群规模大小为2N的新种群Rt。

接着，对Rt进行非支配排序，得到多个非支配集Z_iZi并计算每个个体的拥挤度。由于Rt包含了父代和子代的所有个体，因此排序后的第一非支配集Z_1Z1代表了整个种群中最优的个体。这些个体将优先被选入新的父代种群P_{t+1}Pt+1。如果P_{t+1}Pt+1的规模仍不足NN，则继续加入下一个非支配集Z2，直到加入Z_nZn时，种群大小超过NN。在这种情况下，需要通过拥挤度比较算子，从Zn中挑选出数量合适的个体，确保Pt+1的总规模达到N。

最后，通过遗传算子，如选择、交叉、变异，来产生新的子代种群Qt+1。

算法流程

NSGA-II 算法的基本流程是：

1）随机产生种群规模大小为N的父代种群Pt，然后由父代种群P产生子代种群Qt，其种群规模大小同样为Nt。将两个种群混合在一起，形成了种群规模大小为2N的种群Rt；

2）将合并产生的新种群Rt,进行快速非支配排序。与此同时，还要对处在每个非支配层中的所有个体都进行拥挤度计算，依据个体之间的非支配关系和个体拥挤度的大小，选择合适的个体来组成新的父代种群Pt+1；

3）通过传统的遗传算法的基本操作，如交叉、变异等，产生新的子代种群Qt+1，再将Pt+1与Qt+1，混合一起形成新的种群Rt，重复上述操作，直到满足优化问题结束的条件。

相应的流程图如下图所示。

性能测评

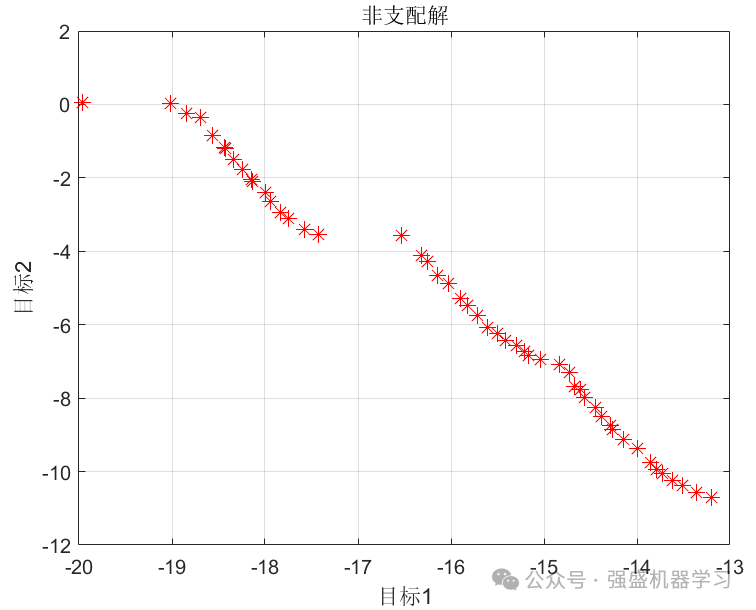
这边以两个多目标函数为例，检测一下NSGA-II的性能。

function z=MOP2(x)

    n=numel(x);
    
    z1=1-exp(-sum((x-1/sqrt(n)).^2));
    
    z2=1-exp(-sum((x+1/sqrt(n)).^2));
    
    z=[z1 z2]';

end

function z=MOP4(x)

    a=0.8;
    
    b=3;
    
    z1=sum(-10*exp(-0.2*sqrt(x(1:end-1).^2+x(2:end).^2)));
    
    z2=sum(abs(x).^a+5*(sin(x)).^b);
    
    z=[z1 z2]';

end

得到的结果如下所示：

参考文献

[1]Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. A. M. T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE transactions on evolutionary computation, 6(2), 182-197.

完整代码

NSGA-II的完整代码如下：

clc;
clear;
close all;

%% Problem Definition

CostFunction=@(x) MOP4(x);      % Cost Function

nVar=3;             % Number of Decision Variables

VarSize=[1 nVar];   % Size of Decision Variables Matrix

VarMin=-5;          % Lower Bound of Variables
VarMax= 5;          % Upper Bound of Variables

% Number of Objective Functions
nObj=numel(CostFunction(unifrnd(VarMin,VarMax,VarSize)));


%% NSGA-II Parameters

MaxIt=100;      % Maximum Number of Iterations

nPop=50;        % Population Size

pCrossover=0.7;                         % Crossover Percentage
nCrossover=2*round(pCrossover*nPop/2);  % Number of Parnets (Offsprings)

pMutation=0.4;                          % Mutation Percentage
nMutation=round(pMutation*nPop);        % Number of Mutants

mu=0.02;                    % Mutation Rate

sigma=0.1*(VarMax-VarMin);  % Mutation Step Size


%% Initialization

empty_individual.Position=[];
empty_individual.Cost=[];
empty_individual.Rank=[];
empty_individual.DominationSet=[];
empty_individual.DominatedCount=[];
empty_individual.CrowdingDistance=[];

pop=repmat(empty_individual,nPop,1);

for i=1:nPop
    
    pop(i).Position=unifrnd(VarMin,VarMax,VarSize);
    
    pop(i).Cost=CostFunction(pop(i).Position);
    
end

% Non-Dominated Sorting
[pop, F]=NonDominatedSorting(pop);

% Calculate Crowding Distance
pop=CalcCrowdingDistance(pop,F);

% Sort Population
[pop, F]=SortPopulation(pop);


%% NSGA-II Main Loop

for it=1:MaxIt
    
    % Crossover
    popc=repmat(empty_individual,nCrossover/2,2);
    for k=1:nCrossover/2
        
        i1=randi([1 nPop]);
        p1=pop(i1);
        
        i2=randi([1 nPop]);
        p2=pop(i2);
        
        [popc(k,1).Position, popc(k,2).Position]=Crossover(p1.Position,p2.Position);
        
        popc(k,1).Cost=CostFunction(popc(k,1).Position);
        popc(k,2).Cost=CostFunction(popc(k,2).Position);
        
    end
    popc=popc(:);
    
    % Mutation
    popm=repmat(empty_individual,nMutation,1);
    for k=1:nMutation
        
        i=randi([1 nPop]);
        p=pop(i);
        
        popm(k).Position=Mutate(p.Position,mu,sigma);
        
        popm(k).Cost=CostFunction(popm(k).Position);
        
    end
    
    % Merge
    pop=[pop
         popc
         popm]; %#ok
     
    % Non-Dominated Sorting
    [pop, F]=NonDominatedSorting(pop);

    % Calculate Crowding Distance
    pop=CalcCrowdingDistance(pop,F);

    % Sort Population
    pop=SortPopulation(pop);
    
    % Truncate
    pop=pop(1:nPop);
    
    % Non-Dominated Sorting
    [pop, F]=NonDominatedSorting(pop);

    % Calculate Crowding Distance
    pop=CalcCrowdingDistance(pop,F);

    % Sort Population
    [pop, F]=SortPopulation(pop);
    
    % Store F1
    F1=pop(F{1});
    
    % Show Iteration Information
    disp(['Iteration ' num2str(it) ': Number of F1 Members = ' num2str(numel(F1))]);
    
    % Plot F1 Costs
    figure(1);
    PlotCosts(F1);
    pause(0.01);
    
end

其中有部分函数封装为了子函数，因篇幅原因文章中无法全部放下。因此，需要完整代码（能够运行出结果展示中的图片）的小伙伴只需点击下方小卡片，再后台回复关键词，不区分大小写：

NSGA2