深度学习笔记其一:基础知识和PYTORCH
为了能够完成各种数据操作,我们需要某种方法来存储和操作数据。 通常,我们需要做两件重要的事:首先,我们介绍 nnn 维数组,也称为。 使用过 Python 中 NumPy 计算包的读者会对本部分很熟悉。 无论使用哪个深度学习框架,它的张量类(在 MXNet 中为 ndarray, 在 PyTorch 和 TensorFlow 中为 Tensor)都与 Numpy 的 ndarray 类似。但深度学
Reference:
- 《动手学深度学习》 强烈建议看原书
文章跳转:
- 深度学习笔记其一:基础知识和PYTORCH
- 深度学习笔记其二:线性神经网络和PYTORCH
- 深度学习笔记其三:多层感知机和PYTORCH
- 深度学习笔记其四:深度学习计算和PYTORCH
- 深度学习笔记其五:卷积神经网络和PYTORCH
- 深度学习笔记其六:现代卷积神经网络和PYTORCH
- 深度学习笔记其七:计算机视觉和PYTORCH
1. 数据操作
为了能够完成各种数据操作,我们需要某种方法来存储和操作数据。 通常,我们需要做两件重要的事:
- 获取数据;
- 将数据读入计算机后对其进行处理。 如果没有某种方法来存储数据,那么获取数据是没有意义的。
首先,我们介绍 n n n 维数组,也称为张量(tensor)。 使用过 Python 中 NumPy(Numerical Python) 计算包的读者会对本部分很熟悉。 无论使用哪个深度学习框架,它的张量类(在 MXNet 中为 ndarray, 在 PyTorch 和 TensorFlow 中为 Tensor) 都与 Numpy 的 ndarray(n-dimension) 类似。但深度学习框架又比 Numpy 的 ndarray 多一些重要功能:首先,张量类支持自动微分。其次,它利用 GPU 来加速数值计算,而 NumPy 仅在 CPU 上运行。这些属性使神经网络既易于编码又运行快速。
1.2 入门
1.2.1 导入 torch
注意,虽然被称为 PyTorch,但是代码中使用 torch 而不是 pytorch。
import torch
1.2.2 张量(tensor)
张量表示由一个数值组成的数组,这个数组可能有多个维度。在一维情况下,即当数据只需要一个轴时,张量称为 向量;具有两个轴的张量对应数学上的矩阵(matrix);如果 k > 2 k>2 k>2 轴,将对象称为 k t h k^{th} kth 阶张量即可。
PyTorch 提供了各种函数来创建预填充值的新张量。例如,通过调用 arange(n) — array range,我们可以创建一个均匀分布的值向量,从 0(含) 开始,到 n(不含) 结束。默认情况下,间隔大小为 1 1 1。除非另有说明,新的张量都存储在主存储器中并指定用于基于 CPU 的计算。
dtype: the desired data type.
# 如不指定dtype,默认数据类型torch.int64
x = torch.arange(12, dtype=torch.float32)
x
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
在张量中,每一个数值都被称为张量的 元素(slement)。张量 x 包含了 12 个元素。
可以通过张量的 shape 属性来访问张量(沿每个轴的长度)的形状:
x.shape
torch.Size([12])
如果只想知道张量中元素的总数,即形状的所有元素乘积,可以检查它的 numel(Number of elements)。
x.numel()
12
要想改变一个张量的形状而不改变元素数量和元素值,可以调用 reshape() 函数。 例如,可以把张量 x x x 从形状为(12,)的行向量转换为形状为 ( 3 , 4 ) (3,4) (3,4) 的矩阵。这个新的张量包含与转换前相同的值,但是它被看成一个 3 3 3 行 4 4 4 列的矩阵。要重点说明一下,虽然张量的形状发生了改变,但其元素值并没有变。注意,通过改变张量的形状,张量的大小不会改变。
X = x.reshape(3, 4)
X
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
我们不需要通过手动指定每个维度来改变形状。也就是说,如果我们的目标形状是(高度,宽度),那么在知道宽度后,高度会被自动计算得出,不必我们自己做除法。在上面的例子中,为了获得一个 3 3 3 行的矩阵,我们手动指定了它有 3 3 3 行和 4 4 4 列。幸运的是,我们可以通过 − 1 -1 −1 来调用此自动计算出维度的功能。即我们可以用 x.reshape(-1,4) 或 x.reshape(3,-1) 来取代 x.reshape(3,4)。
有时,我们希望使用全 0 0 0、全 1 1 1、其他常量,或者从特定分布中随机采样的数字来初始化矩阵。我们可以创建一个形状为(2,3,4)的张量,其中所有元素都设置为 0 0 0。代码如下:(torch.zeros(2, 3, 4) 和 torch.zeros((2, 3, 4)) 都用于创建一个形状为 (2, 3, 4) 的全零张量,但 torch.zeros(2, 3, 4) 是将每个维度的大小作为单独的参数传递;torch.zeros((2, 3, 4)) 是将形状作为一个 元组 传递)
torch.zeros((2, 3, 4))
tensor([[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]],
[[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]])
同样,我们可以创建一个形状为 (2,3,4) 的张量,其中所有元素都设置为 1 1 1。代码如下:
torch.ones((2, 3, 4))
tensor([[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]],
[[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]])
有时我们想通过从某个特定的概率分布中随机采样来得到张量中每个元素的值。例如,当我们构造数组来作为神经网络中的参数时,我们通常会随机初始化参数的值。以下代码创建一个形状为(3,4)的张量。 其中的每个元素都从均值为 0 0 0、标准差为 1 1 1的标准高斯分布(正态分布)中随机采样。
torch.randn(3, 4)
tensor([[-0.5582, -0.0443, 1.6146, 0.6003],
[-1.7652, 1.3074, 0.5233, 1.4372],
[ 0.2452, 2.2281, 1.3483, 0.1783]])
我们还可以通过提供包含数值的 Python list(列表)(或嵌套列表),来为所需张量中的每个元素赋予确定值(直接为 tensor 赋值)。 在这里,最外层的列表对应于轴 0 0 0,内层的列表对应于轴 1 1 1。
torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
#少写一个中括号会报错:
#torch.tensor([2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1])
tensor([[2, 1, 4, 3],
[1, 2, 3, 4],
[4, 3, 2, 1]])
1.3 索引与切片
就像 Python 列表一样,我们可以通过 索引(从 0 0 0 开始)来访问张量元素。要基于相对于列表末尾的位置来访问一个元素,我们可以使用负索引。最后,我们可以通过 切片(比如 X[start:stop])来访问一系列索引,其中返回的值包括第一个索引(start)但不包括最后一个(stop)。最后,当对 k t h k^{th} kth 阶张量仅指定一个索引(或切片)时,它沿着轴 0 0 0 应用。因此在以下代码中,[-1] 选择最后一行,[1:3] 选择第二行和第三行。
X[-1], X[1:3]
(tensor([ 8., 9., 10., 11.]),
tensor([[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]]))
除读取外,我们还可以通过指定索引来将元素写入矩阵:
X[1, 2] = 9
X
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 9., 7.],
[ 8., 9., 10., 11.]])
如果我们想为多个元素赋值相同的值,我们只需要索引所有元素,然后为它们赋值。例如,[0:2, :]访问第1行和第2行(注意第三行都不包括在内),其中 ':' 代表沿轴1(列)的所有元素。虽然我们讨论的是矩阵的索引,但这也适用于向量和超过2个维度的张量。
X[0:2, :] = 12
X
tensor([[12., 12., 12., 12.],
[12., 12., 12., 12.],
[ 8., 9., 10., 11.]])
1.4 运算符
我们的兴趣不仅限于读取数据和写入数据。 我们想在这些数据上执行数学运算,其中最简单且最有用的操作是 逐元素(element-wise)运算。 它们将标准标量运算符应用于数组的每个元素。 对于将两个数组作为输入的函数,按元素运算将二元运算符应用于两个数组中的每对位置对应的元素。 我们可以基于任何从标量到标量的函数来创建按元素函数。
在数学表示法中,我们将通过符号 f : R → R f: \mathbb{R} \rightarrow \mathbb{R} f:R→R 来表示一元标量运算符(只接收一个输入)。 这意味着该函数从任何实数( R \mathbb{R} R)映射到另一个实数。同样,我们通过符号 f : R , R → R f: \mathbb{R}, \mathbb{R} \rightarrow \mathbb{R} f:R,R→R 表示二元标量运算符,这意味着该函数接收两个输入(输入有两个 R \mathbb{R} R),并产生一个输出。 给定同一形状的任意两个向量 u \mathbb{u} u 和 v \mathbb{v} v 和二元运算符 f f f,我们可以得到向量 c = F ( u , v ) \mathbb{c}=F(\mathbb{u},\mathbb{v}) c=F(u,v)。具体计算方法是 c i ← f ( u i , v i ) \mathbb{c_i}\leftarrow f(u_i,v_i) ci←f(ui,vi),其中 c i c_i ci、 u i u_i ui和 v i v_i vi分别是向量 c \mathbb{c} c、 u \mathbb{u} u和 v \mathbb{v} v中的元素。 在这里,我们通过将标量函数升级为按元素向量运算来生成向量值 F : R d , R d → R d F: \mathbb{R}^{d}, \mathbb{R}^{d} \rightarrow \mathbb{R}^{d} F:Rd,Rd→Rd。
对于任意具有相同形状的张量, 常见的标准算术运算符(加+、减-、乘*、除/ 和 指数运算**)都可以被升级为逐元素运算。我们可以在同一形状的任意两个张量上调用按元素操作。在下面的例子中,我们使用 , 来表示一个具有 5 5 5 个元素的元组(说的是 x + y, x - y, x * y, x / y, x ** y 整体组成的元组—在某些场景下,多个值用逗号分隔,会被隐式视为元组),其中每个元素都是按元素操作的结果。
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y # **运算符是求幂运算
(tensor([ 3., 4., 6., 10.]),
tensor([-1., 0., 2., 6.]),
tensor([ 2., 4., 8., 16.]),
tensor([0.5000, 1.0000, 2.0000, 4.0000]),
tensor([ 1., 4., 16., 64.]))
逐元素方式 可以应用更多的计算,包括像求幂这样的一元运算符:
torch.exp(x)
tensor([2.7183e+00, 7.3891e+00, 5.4598e+01, 2.9810e+03])
除了逐元素计算外,我们还可以执行线性代数运算,包括向量点积和矩阵乘法。这将在 线性代数 小结内重点介绍。
我们也可以把多个张量 连结(concatenate) 在一起-----torch.cat,将它们首尾相连堆叠以形成更大的张量。我们只需要提供一个张量列表,并告诉系统沿哪个轴连接即可。下面的例子分别演示了当我们沿行(轴-0,形状的第一个元素)和按列(轴-1,形状的第二个元素)连结两个矩阵时,会发生什么情况。我们可以看到,第一个输出张量的轴-0长度 ( 6 ) (6) (6) 是两个输入张量轴-0长度的总和 ( 3 + 3 ) (3+3) (3+3); 第二个输出张量的轴-1长度 ( 8 ) (8) (8) 是两个输入张量轴-1长度的总和 ( 4 + 4 ) (4+4) (4+4)。
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 2., 1., 4., 3.],
[ 1., 2., 3., 4.],
[ 4., 3., 2., 1.]]),
tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
[ 4., 5., 6., 7., 1., 2., 3., 4.],
[ 8., 9., 10., 11., 4., 3., 2., 1.]]))
有时,我们想通过逻辑运算符构建二元张量。以 X = = Y X == Y X==Y 为例:对于每个位置,如果 X X X 和 Y Y Y 在该位置相等,则新张量中相应项的值为 1 1 1。这意味着逻辑语句 X = = Y X == Y X==Y 在该位置处为真,否则该位置为 0 0 0。
X == Y
tensor([[False, True, False, True],
[False, False, False, False],
[False, False, False, False]])
对张量中的所有元素进行求和-----.sum(),会得到只有一个元素的张量:
X.sum()
tensor(66.)
1.5 广播机制
在上面的部分中,我们看到了如何在相同形状的两个张量上执行按元素操作。在某些情况下,即使形状不同,我们仍然可以通过调用 广播机制(broadcasting mechanism) 来执行按元素操作。这种机制的工作方式如下:
- 通过适当复制元素来扩展其中一个或两个数组均扩展, 以便在转换之后,两个张量具有相同的形状;
- 对生成的数组执行逐元素的操作。
在大多数情况下,我们将沿着数组中长度为1的轴进行广播,如下例子:
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b
(tensor([[0],
[1],
[2]]),
tensor([[0, 1]]))
由于 a 和 b 分别是 3 × 1 3\times 1 3×1 和 1 × 2 1 \times 2 1×2 矩阵,如果让它们相加,它们的形状不匹配。我们将两个矩阵广播为一个更大的矩阵,如下所示:矩阵a将复制列, 矩阵b将复制行,然后再按元素相加。
a + b
tensor([[0, 1],
[1, 2],
[2, 3]])
1.6 Important:节省内存
运行一些操作可能会导致为新结果分配内存。例如,如果我们写 Y = X + Y,就解除了 Y 指向的张量的引用,并让 Y 指向新分配的内存。可以用 Python 的 id() 函数来演示这个问题,该函数可以提供内存中被引用对象的确切地址。运行 Y = Y + X 后,我们会发现 id(Y) 指向另一个位置。 这是因为 Python 首先计算 Y + X,为结果分配新的内存,然后使 Y 指向内存中的这个新位置。
before = id(Y)
Y = Y + X
id(Y) == before
False
这可能是不可取的,原因有两个:
- 我们不想总是不必要地分配内存。 在机器学习中,我们可能有数百兆的参数,并且在一秒内多次更新所有参数。 通常情况下,我们希望原地执行这些更新;
- 其次,如果我们不原地更新,其他引用仍然会指向旧的内存位置, 这样我们的某些代码可能会无意中引用旧的参数。
幸运的是,执行原地操作非常简单。我们可以使用 切片表示法 将操作的结果分配给先前分配的数组,例如 Y[:] = <expression>。为了说明这一点,我们首先创建一个新的矩阵 Z,其形状与另一个 Y 相同,使用 zeros_like 来分配一个全的块。
Z = torch.zeros_like(Y)
print('id(Z):', id(Z))
Z = X + Y ##这里地址发生了改变
print('id(Z):', id(Z))
Z[:] = X + Y ##使用切片法后,地址就没有变化了
print('id(Z):', id(Z))
id(Z): 140436617266896
id(Z): 140436623436272
id(Z): 140436623436272
如果在后续计算中没有重复使用X,我们也可以使用 X[:] = X + Y 或 X += Y 来减少操作的内存开销。
before = id(X)
X += Y
id(X) == before
True
1.7 转换为其他Python对象
将深度学习框架定义的张量转换为 NumPy tensor/张量(ndarray)很容易(就像上面说的,广义的 tensor 表示由一个数值组成的数组,这个数组可能有多个维度),反之也同样容易。torch tensor 和 numpy array 将共享它们的底层内存,就地操作更改一个张量也会同时更改另一个张量-----torch.tensor():
A = X.numpy()
B = torch.tensor(A)
type(A), type(B)
(numpy.ndarray, torch.Tensor)
要将大小为 1 的 张量 转换为 Python 标量,我们可以调用 item() 函数或 Python 的内置函数:
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
(tensor([3.5000]), 3.5, 3.5, 3)
1.8 小结
张量类是深度学习库中存储和操作数据的主要接口。它提供了各种功能,包括基本数学运算、广播、索引、切片、内存节省和转换其他 Python 对象。
2. 数据预处理
到目前为止,我们一直在使用现成张量形式的合成数据。然而,要在实际应用中使用深度学习,我们必须提取以任意格式存储的杂乱数据,并对其进行预处理以满足我们的需求。幸运的是,pandas(Panel Data + Python Data Analysis) 库可以完成大部分繁重的工作。本节虽然不能替代适当的 pandas 教程,但将为你快速介绍一些最常见的例程。
2.1 读取数据集
逗号分隔值(Comma-separated values, CSV) 文件普遍用于存储表格(类似电子表格)数据。在这些文件中,每一行对应一条记录,由几个(逗号分隔的)字段组成。
为了示范如何使用 pandas 加载 CSV 文件,我们创建了一个 CSV 文件 ../data/house_tiny.csv。这个文件代表了一个房屋数据集,其中每一行对应一个不同的房屋,列对应房间数量(NumRooms)、胡同(Alley)、价格(Price):
# 创建的 CSV 文件:../data/house_tiny.csv
import os
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每行表示一个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
现在让我们导入 pandas 库,并使用 read_csv 函数来加载数据集。
# 如果没有安装pandas,只需取消对以下行的注释来安装pandas
# !pip install pandas
import pandas as pd
data = pd.read_csv(data_file)
print(data)
NumRooms Alley Price
0 NaN Pave 127500
1 2.0 NaN 106000
2 4.0 NaN 178100
3 NaN NaN 140000
2.2 处理缺失值
注意,NaN项代表缺失值。为了处理缺失的数据,典型的方法包括 插值法 和 删除法,其中插值法 用一个替代值弥补缺失值,而 删除法 则直接忽略缺失值。在这里,我们将考虑 插值法:
通过位置索引 iloc,我们将 data 分成 inputs 和 targets, 其中前者为 data 的前两列,而后者为 data 的最后一列。对于 inputs 中缺少的数值,我们用同一列的均值替换 NaN 项(插值法 1)。
inputs, targets = data.iloc[:, 0:2], data.iloc[:, 2]
print(inputs)
NumRooms Alley
0 NaN Pave
1 2.0 NaN
2 4.0 NaN
3 NaN NaN
对于 inputs 中的类别值或离散值,我们将“NaN”视为一个类别。由于“巷子类型”(“Alley”)列只接受两种类型的类别值 “Pave” 和 “NaN”,pandas 可以自动将此列转换为两列“Alley_Pave”和“Alley_nan”。巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1,“Alley_nan” 的值设置为0。 缺少巷子类型的行会将“Alley_Pave”和“Alley_nan”分别设置为0和1(pandas.get_dummies(one-hot encoding): 将离散型特征的每一种取值都看成一种状态,若你的这一特征中有N个不相同的取值,那么我们就可以将该特征抽象成N种不同的状态,one-hot 编码保证了每一个取值只会使得一种状态处于“激活态”,也就是说这N种状态中只有一个状态位值为1,其他状态位都是0)。
inputs = pd.get_dummies(inputs, dummy_na=True)
inputs = inputs.fillna(inputs.mean()) # 这个放前一行因为有多的NaN会报错
print(inputs)
NumRooms Alley_Pave Alley_nan
0 3.0 1 0
1 2.0 0 1
2 4.0 0 1
3 3.0 0 1
2.3 转换为张量格式
现在 inputs 和 targets 中的所有条目都是数值类型,它们可以转换为张量格式。当数据采用张量格式后,可以通过在上一节中引入的那些张量函数来进一步操作。
import torch
X = torch.tensor(inputs.to_numpy(dtype=float))
y = torch.tensor(targets.to_numpy(dtype=float))
X, y
(tensor([[3., 1., 0.],
[2., 0., 1.],
[4., 0., 1.],
[3., 0., 1.]], dtype=torch.float64),
tensor([127500, 106000, 178100, 140000], dtype=torch.float64))
2.4 小结
- pandas 软件包是 Python 中常用的数据分析工具中,pandas 可以与张量兼容。
- 用 pandas 处理缺失的数据时,我们可根据情况选择用
插值法和删除法。
3. 线性代数
现在已经可以存储和操作数据后,简要地回顾一下部分基本线性代数内容。这些内容能够帮助了解和实现将会介绍的大多数模型。本节将介绍线性代数中的基本数学对象、算术和运算,并用数学符号和相应的代码实现来表示它们。
3.1 标量
如果你曾经在餐厅支付餐费,那么你已经知道一些基本的线性代数,比如在数字间相加或相乘。例如,北京的温度为 52 ° F 52°F 52°F(除了摄氏度外,另一种温度计量单位)。 严格来说,我们称仅包含一个数值的叫 标量(scalar)。如果要将此华氏度值转换为更常用的摄氏度, 则可以计算表达式 c = 5 9 ( f − 32 ) c=\frac{5}{9}(f-32) c=95(f−32),并将 f f f 赋为 52 52 52。在此等式中,每一项( 5 5 5、 9 9 9 和 32 32 32)都是标量值。符号 c c c 和 f f f 称为变量(variable),它们表示 未知的标量(unknown scalar)。
数学表示法中,标量变量由普通小写字母表示(例如, x x x、 y y y 和 z z z)。用 R \mathbb{R} R 表示所有(连续)实数标量的空间。之后将严格定义空间(space)是什么, 但现在要记住表达式 x ∈ R x\in \mathbb{R} x∈R 是表示 x x x 是一个实值标量的正式形式。符号 ∈ \in ∈ 称为“属于”,它表示“是集合中的成员”。我们可以用 x , y ∈ { 0 , 1 } x,y\in \{0,1\} x,y∈{0,1} 来表明 x x x 和 y y y 是值只能为 0 0 0 或 1 1 1 的数字。
标量由只有一个元素的 张量(tensor) 表示。 在下面的代码中,我们实例化两个标量,并执行一些熟悉的算术运算,即加法、乘法、除法和指数。
import torch
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x**y
(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.))
3.2 向量
在当前的用途中,可以将 向量 视为一个固定长度的标量数组。与代码中的数组类似,我们称这些标量为向量的 元素(element)/条目(entry)/分量(component)。
当向量代表现实世界数据集中的示例时,其值具有现实世界的意义。例如,如果我们正在训练一个模型来预测贷款违约的风险,我们可能会将每个申请人与一个向量关联起来,其分量对应于他们的收入、工作年限或以前违约的次数等数量。如果我们正在研究心脏病发作的风险,每个向量可能代表一个患者,其分量可能对应于他们最近的生命体征、胆固醇水平、每天锻炼的分钟数等。
我们用粗体小写字母来表示 向量(例如, x \mathbf{x} x、 y \mathbf{y} y、 z \mathbf{z} z)。
向量被实现为 1 s t 1^{st} 1st 阶张量。一般来说,这样的张量可以有任意长度,受内存限制的约束。
注意:
- 在 Python 中,像大多数编程语言一样,向量索引从 0 开始,也称为
零基索引(zero-based indexing); - 而在线性代数中,下标从 1 开始,也称为
一基索引(one-based indexing)
x = torch.arange(4)
x
tensor([0, 1, 2, 3])
我们可以使用下标来引用向量的任一元素。例如,我们可以通过 x i x_i xi 来引用第 i i i 个元素。注意,元素 x i x_i xi 是一个 标量,所以我们在引用它时不会加粗。大量文献认为列向量是向量的默认方向,在本书中也是如此。在数学中,向量 x \mathbf{x} x 可以写为:
x = [ x 1 x 2 ⋮ x n ] \mathbf{x}=\left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{array}\right] x=
x1x2⋮xn
其中 x 1 , . . . , x n x_1,...,x_n x1,...,xn 是向量的元素。稍后,将区分 列向量 和 行向量,后者的元素是水平堆叠的。在代码中,我们通过张量的索引来访问任一元素。
x[3]
tensor(3)
3.2.1 长度、维度和形状
要表示一个向量包含 n n n 个元素,我们写作 x ∈ R n \mathbf{x}\in \mathbb{R}^n x∈Rn。形式上,我们称 n n n 为向量的维数。在代码中,这对应于张量的长度,可以通过 Python 的内置 len() 函数访问.
len(x)
4
- len 二维数组:
rows = len(array) cols = len(array[0])
我们也可以通过 shape 属性来访问长度。shape 是一个元组,表示张量在每个轴上的长度。只有一轴的张量的 shape 只有一个元素。(注意与上面的 len 是有些区别的,比如一个 X ∈ R 4 × 3 \mathbf{X}\in \mathbb{R}^{4\times 3} X∈R4×3,len 返回值为 4 4 4,shape 返回值为 torch.Size([4, 3]))
x.shape
torch.Size([4])
通常情况下,维度(dimension) 这个词被过度使用,既可以指轴的数量,也可以指某个特定轴上的长度。为了避免这种混淆,我们用 阶数(order) 来指代轴的数量,而用 维度性 专门指代分量的数量.
3.3 矩阵
正如 向量 将 标量 从零阶推广到一阶,矩阵 将 向量 从一阶推广到二阶。矩阵,我们通常用粗体、大写字母来表示(例如, X \mathbf{X} X、 Y \mathbf{Y} Y、 Z \mathbf{Z} Z),在代码中表示为具有两个轴的张量。
在数学表示法中,我们使用 A ∈ R m × n \mathbf{A}\in \mathbb{R}^{m\times n} A∈Rm×n 来表示矩阵 A \mathbf{A} A,其由 m m m 行和 n n n 列的实值标量组成。我们可以将任意矩阵 A ∈ R m × n \mathbf{A}\in \mathbb{R}^{m\times n} A∈Rm×n 视为一个表格, 其中每个元素 a i j a_{ij} aij 属于第 i i i 行第 j j j 列:
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] \mathbf{A}=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m n} \end{array}\right] A=
a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn
对于任意 A ∈ R m × n \mathbf{A}\in \mathbb{R}^{m\times n} A∈Rm×n, A \mathbf{A} A 的形状是 ( m , n ) (m,n) (m,n) 或 m × n m\times n m×n。当矩阵具有相同数量的行和列时,其形状将变为正方形;因此,它被称为 方阵(square matrix)。
当调用函数来实例化张量时, 我们可以通过指定两个分量 m m m 和 n n n 来创建一个形状为 m × n m\times n m×n 的矩阵。
A = torch.arange(20).reshape(5, 4)
A
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
我们可以通过行索引 ( i ) (i) (i)和列索引 ( j ) (j) (j)来访问矩阵中的标量元素 a i j a_{ij} aij,例如 [ A ] i j [\mathbf{A}]_{ij} [A]ij。如果没有给出矩阵 A \mathbf{A} A 的标量元素,可以简单地使用矩阵 A \mathbf{A} A 的小写字母索引下标 a i j a_{ij} aij 来引用 [ A ] i j [\mathbf{A}]_{ij} [A]ij。为了表示起来简单,只有在必要时才会将逗号插入到单独的索引中, 例如 a 2 , 3 j a_{2,3j} a2,3j 和 [ A ] 2 i − 1 , 3 [\mathbf{A}]_{2i-1,3} [A]2i−1,3。
当我们交换矩阵的行和列时,结果称为矩阵的 转置(transpose)。我们用 A T \mathbf{A}^T AT 来表示矩阵的转置,如果 B = A T \mathbf{B} = \mathbf{A}^T B=AT,则对于任意 i i i 和 j j j,都有。 因此,在 (2.3.2)中的转置是一个形状为的矩阵:
A T = [ a 11 a 21 ⋯ a m 1 a 12 a 22 ⋯ a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ a m n ] \mathbf{A^T}=\left[\begin{array}{cccc} a_{11} & a_{21} & \cdots & a_{m 1} \\ a_{12} & a_{22} & \cdots & a_{m 2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1 n} & a_{2 n} & \cdots & a_{m n} \end{array}\right] AT=
a11a12⋮a1na21a22⋮a2n⋯⋯⋱⋯am1am2⋮amn
现在我们在代码中访问矩阵的转置。
A.T
tensor([[ 0, 4, 8, 12, 16],
[ 1, 5, 9, 13, 17],
[ 2, 6, 10, 14, 18],
[ 3, 7, 11, 15, 19]])
作为方阵的一种特殊类型,对称矩阵(symmetric matrix) A \mathbf{A} A 等于其转置: A = A T \mathbf{A}=\mathbf{A}^T A=AT。 这里我们定义一个对称矩阵 B \mathbf{B} B:
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
tensor([[1, 2, 3],
[2, 0, 4],
[3, 4, 5]])
现在我们将 B \mathbf{B} B 与它的转置进行比较。
B == B.T
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
矩阵是有用的数据结构:它们允许我们组织具有不同模式的数据。例如,我们矩阵中的行可能对应于不同的房屋(数据样本),而列可能对应于不同的属性。因此,尽管单个向量的默认方向是列向量,但在表示表格数据集的矩阵中,将每个数据样本作为矩阵中的行向量更为常见。
3.4 张量
就像 向量 是 标量 的推广,矩阵 是 向量 的推广一样,我们可以构建具有更多轴的数据结构。张量(本小节中的“张量”指代数对象)为我们提供了描述具有任意数量轴的维数组的通用方法。例如,向量是一阶张量,矩阵是二阶张量。张量用特殊字体的大写字母表示(例如, X \mathsf{X} X、 Y \mathsf{Y} Y 和 Z \mathsf{Z} Z)(理论上应该与矩阵有区分,有的地方写的 X \mathcal{X} X、 Y \mathcal{Y} Y 和 Z \mathcal{Z} Z), 它们的索引机制(例如 x i j k x_{ijk} xijk 和 [ X ] 1 , 2 i − 1 , 3 [\mathbf{X}]_{1,2i-1,3} [X]1,2i−1,3)与矩阵类似。
当我们开始处理图像时,张量将变得更加重要。每张图像以一个 3 r d 3^{rd} 3rd 阶张量的形式到达,其轴对应于高度、宽度和通道。在每个空间位置,每种颜色(红色、绿色和蓝色)的强度沿通道堆叠。此外,一组图像在代码中由一个 4 t h 4^{th} 4th 张量表示,其中不同的图像沿第一个轴进行索引。高阶张量的构造方式与向量和矩阵相同,通过增加形状组件的数量来实现。
X = torch.arange(24).reshape(2, 3, 4)
X
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
3.5 张量算法的基本性质
标量、向量、矩阵和任意数量轴的张量(本小节中的“张量”指代数对象)有一些实用的属性。例如,你可能已经从按元素操作的定义中注意到,任何按元素的一元运算都不会改变其操作数的形状。同样,给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。例如,将两个相同形状的矩阵相加,会在这两个矩阵上执行元素加法。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
A, A + B
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]]),
tensor([[ 0., 2., 4., 6.],
[ 8., 10., 12., 14.],
[16., 18., 20., 22.],
[24., 26., 28., 30.],
[32., 34., 36., 38.]]))
具体而言,两个矩阵的按元素乘法称为 Hadamard积(Hadamard product)(数学符号 ⊙ \odot ⊙)。对于矩阵 B ∈ R m × n \mathbf{B}\in \mathbb{R}^{m\times n} B∈Rm×n, 其中第 i i i 行和第 j j j 列的元素是 b i j b_{ij} bij。矩阵 A \mathbf{A} A 和 B \mathbf{B} B 的Hadamard积为(* 就是按元素相乘):
A ⊙ B = [ a 11 b 11 a 12 b 12 … a 1 n b 1 n a 21 b 21 a 22 b 22 … a 2 n b 2 n ⋮ ⋮ ⋱ ⋮ a m 1 b m 1 a m 2 b m 2 … a m n b m n ] \mathbf{A} \odot \mathbf{B}=\left[\begin{array}{cccc} a_{11} b_{11} & a_{12} b_{12} & \ldots & a_{1 n} b_{1 n} \\ a_{21} b_{21} & a_{22} b_{22} & \ldots & a_{2 n} b_{2 n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m 1} b_{m 1} & a_{m 2} b_{m 2} & \ldots & a_{m n} b_{m n} \end{array}\right] A⊙B=
a11b11a21b21⋮am1bm1a12b12a22b22⋮am2bm2……⋱…a1nb1na2nb2n⋮amnbmn
A * B
tensor([[ 0., 1., 4., 9.],
[ 16., 25., 36., 49.],
[ 64., 81., 100., 121.],
[144., 169., 196., 225.],
[256., 289., 324., 361.]])
将 张量 乘以或加上一个 标量 不会改变 张量 的形状,其中 张量 的每个元素都将与 标量 相加或相乘。
a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape
(tensor([[[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[22, 23, 24, 25]]]),
torch.Size([2, 3, 4]))
3.6 降维
我们可以对任意张量进行的一个有用的操作是计算其元素的和。在数学表示法中,我们使用 ∑ \sum ∑ 符号表示求和。为了表示长度为 d d d 的向量中元素的总和,可以记为 ∑ i = 0 d x i \sum^d_{i=0}x_i ∑i=0dxi。在代码中,我们可以调用计算求和的函数:
x = torch.arange(4, dtype=torch.float32)
x, x.sum()
(tensor([0., 1., 2., 3.]), tensor(6.))
我们可以表示任意形状张量的元素和。例如,矩阵 A \mathbf{A} A 中元素的和可以记为 ∑ i = 1 m ∑ j = 1 n a i j \sum^m_{i=1}\sum^n_{j=1}a_{ij} ∑i=1m∑j=1naij。
A.shape, A.sum()
(torch.Size([5, 4]), tensor(190.))
默认情况下,调用求和函数会沿所有的轴降低张量的维度,使它变为一个标量。 我们还可以指定张量沿哪一个轴来通过求和降低维度。以矩阵为例,为了通过求和所有行的元素来降维(轴0),我们可以在调用函数时指定 a x i s = 0 axis=0 axis=0。 由于输入矩阵沿 0 0 0 轴降维以生成输出向量,因此输入轴 0 0 0 的维数在输出形状中消失。
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
0 + 4 + 8 + 12 + 16 = 40 0+4+8+12+16=40 0+4+8+12+16=40
(tensor([40., 45., 50., 55.]), torch.Size([4]))
指定 a x i s = 1 axis=1 axis=1 将通过汇总所有列的元素降维(轴1)。因此,输入轴1的维数在输出形状中消失。
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
0 + 1 + 2 + 3 = 6 0+1+2+3=6 0+1+2+3=6
(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))
沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和:
A.sum(axis=[0, 1]) # SameasA.sum()
tensor(190.)
一个与求和相关的量是平均值(mean或average)。 我们通过将总和除以元素总数来计算平均值。 在代码中,我们可以调用函数来计算任意形状张量的平均值。
A.mean(), A.sum() / A.numel()
(tensor(9.5000), tensor(9.5000))
同样,计算平均值的函数也可以沿指定轴降低张量的维度。
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
(tensor([ 8., 9., 10., 11.]), tensor([ 8., 9., 10., 11.]))
3.6.1 非降维求和
但是,有时在调用函数来计算总和或均值时保持轴数不变会很有用。
A.mean(), A.sum() / A.numel()
tensor([[ 6.],
[22.],
[38.],
[54.],
[70.]])
例如,由于sum_A在对每行进行求和后仍保持两个轴,我们可以通过广播将A除以sum_A。
A / sum_A
tensor([[0.0000, 0.1667, 0.3333, 0.5000],
[0.1818, 0.2273, 0.2727, 0.3182],
[0.2105, 0.2368, 0.2632, 0.2895],
[0.2222, 0.2407, 0.2593, 0.2778],
[0.2286, 0.2429, 0.2571, 0.2714]])
如果我们想沿某个轴计算A元素的累积总和,比如 a x i s = 0 axis=0 axis=0 (按行计算),我们可以调用 cumsum 函数。 此函数不会沿任何轴降低输入张量的维度。
A.cumsum(axis=0)
tensor([[ 0., 1., 2., 3.],
[ 4., 6., 8., 10.],
[12., 15., 18., 21.],
[24., 28., 32., 36.],
[40., 45., 50., 55.]])
3.7 点积
我们已经学习了按元素操作、求和及平均值。另一个最基本的操作之一是点积。给定两个向量 x , y ∈ R d \mathbf{x},\mathbf{y} \in \mathbb{R}^d x,y∈Rd,它们的点积(dot product) x T y \mathbf{x}^T\mathbf{y} xTy (或 ⟨ x , y ⟩ \langle\mathbf{x}, \mathbf{y}\rangle ⟨x,y⟩) 是相同位置的按元素乘积的和 x T y = ∑ i = 1 d x i y i \mathbf{x}^T\mathbf{y}=\sum^d_{i=1}x_iy_i xTy=∑i=1dxiyi:
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)
(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
注意,我们可以通过执行按元素乘法,然后进行求和来表示两个向量的点积:
torch.sum(x * y)
tensor(6.)
点积在很多场合都很有用。例如,给定一组由向量 x ∈ R d \mathbf{x}\in \mathbb{R}^d x∈Rd 表示的值,和一组由 w ∈ R d \mathbf{w}\in \mathbb{R}^d w∈Rd 表示的权重。 x \mathbf{x} x 中的值根据权重 w \mathbf{w} w 的加权和,可以表示为点积 x T w \mathbf{x}^T\mathbf{w} xTw。 当权重为非负数且和为 1 1 1(即 ( ∑ i = 1 d w i = 1 ) (\sum^d_{i=1}w_i=1) (∑i=1dwi=1))时,点积表示 加权平均(weighted average)。 将两个向量规范化得到单位长度后,点积表示它们夹角的余弦。
3.8 矩阵-向量积
现在我们知道如何计算点积,我们可以开始理解矩阵-向量积(matrix-vector product)。回顾分别在 (3.2) 和 (3.1) 中定义的矩阵 A ∈ R m × n \mathbf{A}\in \mathbb{R}^{m\times n} A∈Rm×n 和向量 x ∈ R n \mathbf{x}\in \mathbb{R}^{n} x∈Rn。让我们将矩阵 A \mathbf{A} A 用它的行向量表示:
A = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] , \mathbf{A}=\left[\begin{array}{c} \mathbf{a}_{1}^{\top} \\ \mathbf{a}_{2}^{\top} \\ \vdots \\ \mathbf{a}_{m}^{\top} \end{array}\right] , A=
a1⊤a2⊤⋮am⊤
,其中每个 a i T ∈ R n \mathbf{a_i}^T\in \mathbb{R}^{n} aiT∈Rn 都是行向量,表示矩阵的第 i i i 行。矩阵向量积 A x \mathbf{Ax} Ax 是一个长度为 m m m 的列向量,其第 i i i 个元素是点积 a i T x \mathbf{a_i}^T\mathbf{x} aiTx(这样解释还蛮有意思的):
A x = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] x = [ a 1 ⊤ x a 2 ⊤ x ⋮ a m ⊤ x ] \mathbf{A} \mathbf{x}=\left[\begin{array}{c} \mathbf{a}_{1}^{\top} \\ \mathbf{a}_{2}^{\top} \\ \vdots \\ \mathbf{a}_{m}^{\top} \end{array}\right] \mathbf{x}=\left[\begin{array}{c} \mathbf{a}_{1}^{\top} \mathbf{x} \\ \mathbf{a}_{2}^{\top} \mathbf{x} \\ \vdots \\ \mathbf{a}_{m}^{\top} \mathbf{x} \end{array}\right] Ax=
a1⊤a2⊤⋮am⊤
x=
a1⊤xa2⊤x⋮am⊤x
我们可以把一个矩阵 A ∈ R m × n \mathbf{A}\in \mathbb{R}^{m\times n} A∈Rm×n 乘法看作是一个从 R n \mathbb{R}^{n} Rn 到 R m \mathbb{R}^{m} Rm 向量的转换。这些转换是非常有用的。例如,我们可以用方阵的乘法来表示旋转;也可以使用矩阵-向量积来描述在给定前一层的值时,求解神经网络每一层所需的复杂计算。
在代码中使用张量表示 矩阵-向量积,会使用到函数 mv(matrix-vector)。 当我们为矩阵 A \mathbf{A} A 和向量 x \mathbf{x} x 调用 torch.mv(A, x) 时,会执行矩阵-向量积。注意, A \mathbf{A} A 的列维数(沿轴1的长度)必须与 x \mathbf{x} x 的维数(其长度)相同。
A.shape, x.shape, torch.mv(A, x)
(torch.Size([5, 4]), torch.Size([4]), tensor([ 14., 38., 62., 86., 110.]))
可见乘出来是一个一维向量。
3.9 矩阵-矩阵乘法
如果你已经掌握了 点积 和 矩阵-向量积 的知识,那么 矩阵-矩阵乘法(matrix-matrix multiplication) 应该很简单。
假设我们有两个矩阵 A ∈ R n × k \mathbf{A}\in \mathbb{R}^{n\times k} A∈Rn×k 和 B ∈ R k × m \mathbf{B}\in \mathbb{R}^{k\times m} B∈Rk×m:
A = [ a 11 a 12 ⋯ a 1 k a 21 a 22 ⋯ a 2 k ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n k ] , B = [ a 11 a 12 ⋯ a 1 m a 21 a 22 ⋯ a 2 m ⋮ ⋮ ⋱ ⋮ a k 1 a k 2 ⋯ a k m ] \mathbf{A}=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 k} \\ a_{21} & a_{22} & \cdots & a_{2 k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n k} \end{array}\right], \mathbf{B}=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 m} \\ a_{21} & a_{22} & \cdots & a_{2 m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{k 1} & a_{k 2} & \cdots & a_{k m} \end{array}\right] A=
a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1ka2k⋮ank
,B=
a11a21⋮ak1a12a22⋮ak2⋯⋯⋱⋯a1ma2m⋮akm
用行向量 a i T ∈ R k \mathbf{a_i}^T\in \mathbb{R}^{k} aiT∈Rk 表示矩阵 A \mathbf{A} A 的第 i i i 行,并让列向量 b j ∈ R k \mathbf{b_j}\in \mathbb{R}^{k} bj∈Rk 作为矩阵 B \mathbf{B} B 的第 j j j 列。要生成矩阵积 C = A B \mathbf{C}=\mathbf{A}\mathbf{B} C=AB,最简单的方法是考虑 A \mathbf{A} A 的行向量和 B \mathbf{B} B 的列向量:
A = [ a 1 ⊤ a 2 ⊤ ⋮ a n ⊤ ] , B = [ b 1 b 2 ⋯ b m ] . \mathbf{A}=\left[\begin{array}{c} \mathbf{a}_{1}^{\top} \\ \mathbf{a}_{2}^{\top} \\ \vdots \\ \mathbf{a}_{n}^{\top} \end{array}\right], \mathbf{B}=\left[\begin{array}{llll} \mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{m} \end{array}\right]. A=
a1⊤a2⊤⋮an⊤
,B=[b1b2⋯bm].当我们简单地将每个元素 c i j c_{ij} cij 计算为点积 a i T b j \mathbf{a_i}^T\mathbf{b_j} aiTbj:
C = A B = [ a 1 ⊤ a 2 ⊤ ⋮ a n ⊤ ] [ b 1 b 2 ⋯ b m ] = [ a 1 ⊤ b 1 a 1 ⊤ b 2 ⋯ a 1 ⊤ b m a 2 ⊤ b 1 a 2 ⊤ b 2 ⋯ a 2 ⊤ b m ⋮ ⋮ ⋱ ⋮ a n ⊤ b 1 a n ⊤ b 2 ⋯ a n ⊤ b m ] \mathbf{C}=\mathbf{A B}=\left[\begin{array}{c} \mathbf{a}_{1}^{\top} \\ \mathbf{a}_{2}^{\top} \\ \vdots \\ \mathbf{a}_{n}^{\top} \end{array}\right]\left[\begin{array}{llll} \mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{m} \end{array}\right]=\left[\begin{array}{cccc} \mathbf{a}_{1}^{\top} \mathbf{b}_{1} & \mathbf{a}_{1}^{\top} \mathbf{b}_{2} & \cdots & \mathbf{a}_{1}^{\top} \mathbf{b}_{m} \\ \mathbf{a}_{2}^{\top} \mathbf{b}_{1} & \mathbf{a}_{2}^{\top} \mathbf{b}_{2} & \cdots & \mathbf{a}_{2}^{\top} \mathbf{b}_{m} \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{a}_{n}^{\top} \mathbf{b}_{1} & \mathbf{a}_{n}^{\top} \mathbf{b}_{2} & \cdots & \mathbf{a}_{n}^{\top} \mathbf{b}_{m} \end{array}\right] C=AB=
a1⊤a2⊤⋮an⊤
[b1b2⋯bm]=
a1⊤b1a2⊤b1⋮an⊤b1a1⊤b2a2⊤b2⋮an⊤b2⋯⋯⋱⋯a1⊤bma2⊤bm⋮an⊤bm
我们可以将矩阵-矩阵乘法 A B \mathbf{A}\mathbf{B} AB 看作是简单地执行 m m m 次矩阵-向量积,并将结果拼接在一起,形成一个 n × m n\times m n×m 矩阵。在下面的代码中,我们在 A \mathbf{A} A 和 B \mathbf{B} B 上执行矩阵乘法。 这里的 A \mathbf{A} A 是一个 5 5 5 行 4 4 4 列的矩阵, B \mathbf{B} B 是一个 4 4 4 行 3 3 3 列的矩阵。两者相乘后,我们得到了一个 5 5 5 行 3 3 3 列的矩阵。注意是 mm(matrix-matrix) 不是 mv(matrix-vector) 了
B = torch.ones(4, 3)
torch.mm(A, B)
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]])
矩阵-矩阵乘法可以简单地称为矩阵乘法。
矩阵-向量乘法:torch.mv,矩阵-矩阵乘法:torch.mm,通用:torch.matmul,用法相同
3.10 范数
线性代数中最有用的一些运算符是范数(norm)。非正式地说,一个向量的范数告诉我们一个向量有多大。这里考虑的大小(size)概念不涉及维度,而是分量的大小。
在线性代数中,向量范数 是将向量映射到标量的函数 f f f。给定任意向量 x \mathbf{x} x,向量范数要满足一些属性:
-
第一个性质是:如果我们按常数因子 α \alpha α 缩放向量的所有元素, 其范数也会按相同常数因子的绝对值缩放:
f ( α x ) = ∣ α ∣ f ( x ) . f(\alpha \mathbf{x}) = |\alpha|f(\mathbf{x}). f(αx)=∣α∣f(x). -
第二个性质是我们熟悉的三角不等式:
f ( x + y ) ≤ f ( x ) + f ( y ) . f(\mathbf{x}+\mathbf{y}) \le f(\mathbf{x})+f(\mathbf{y}). f(x+y)≤f(x)+f(y). -
第三个性质简单地说范数必须是非负的:
f ( x ) ≥ 0 f(\mathbf{x}) \ge 0 f(x)≥0 -
最后一个性质要求范数最小为 0 0 0,当且仅当向量全由 0 0 0 组成:
∀ i , [ x ] i = 0 ⇔ f ( x ) = 0 \forall i,[\mathbf{x}]_{i}=0 \Leftrightarrow f(\mathbf{x})=0 ∀i,[x]i=0⇔f(x)=0
你可能会注意到,范数听起来很像距离的度量。如果你还记得欧几里得距离和毕达哥拉斯定理,那么非负性的概念和三角不等式可能会给你一些启发。事实上,欧几里得距离是一个范数:假设维向量中的元素是,其范数是向量元素平方和的平方根:
∥ x ∥ 2 = ∑ i = 1 n x i 2 \|\mathbf{x}\|_{2}=\sqrt{\sum_{i=1}^{n} x_{i}^{2}} ∥x∥2=i=1∑nxi2其中,在 L 2 L_2 L2 范数中常常省略下标 2 2 2,也就是说 ∥ x ∥ \|\mathbf{x}\| ∥x∥ 等同于 ∥ x ∥ 2 \|\mathbf{x}\|_2 ∥x∥2。在代码中,我们可以按如下方式计算向量的 L 2 L_2 L2 范数。
u = torch.tensor([3.0, -4.0])
torch.norm(u)
tensor(5.)
在深度学习中,我们更经常地使用 L 2 L_2 L2 范数的平方。你还会经常遇到 L 1 L_1 L1 范数,它表示为向量元素的绝对值之和:
∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ \|\mathbf{x}\|_{1}={\sum_{i=1}^{n} |x_i| } ∥x∥1=i=1∑n∣xi∣
与 L 2 L_2 L2 范数相比, L 1 L_1 L1 范数受异常值的影响较小。为了计算 L 1 L_1 L1 范数,我们将绝对值函数和按元素求和组合起来。
torch.abs(u).sum()
tensor(7.)
L 2 L_2 L2 范数和 L 1 L_1 L1 范数都是更一般的 L p L_p Lp 范数的特例:
∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 / p \|\mathbf{x}\|_{p}=({\sum_{i=1}^{n} |x_i|^p)^{1/p}} ∥x∥p=(i=1∑n∣xi∣p)1/p类似于向量的 L 2 L_2 L2 范数,矩阵 X ∈ R m × n \mathbf{X}\in\mathbb{R}^{m\times n} X∈Rm×n 的 Frobenius 范数(Frobenius norm) 是矩阵元素平方和的平方根(一个是向量,一个是矩阵的区别):
∥ X ∥ F = ∑ i = 1 m ∑ j = 1 n x i j 2 \|\mathbf{X}\|_{F}=\sqrt{\sum_{i=1}^{m}\sum_{j=1}^{n} x_{ij}^{2}} ∥X∥F=i=1∑mj=1∑nxij2Frobenius 范数满足向量范数的所有性质,它就像是矩阵形向量的 L 2 L_2 L2 范数。调用以下函数将计算矩阵的 Frobenius 范数。
torch.norm(torch.ones((4, 9)))
tensor(6.)
3.10.1 范数和目标
在深度学习中,我们经常试图解决优化问题:最大化分配给观测数据的概率;最小化预测和真实观测之间的距离。用向量表示物品(如单词、产品或新闻文章),以便最小化相似项目之间的距离,最大化不同项目之间的距离。目标,或许是深度学习算法最重要的组成部分(除了数据),通常被表达为范数。
3.11 小结
- 标量、向量、矩阵和张量是线性代数中的基本数学对象;
- 向量泛化自标量,矩阵泛化自向量;
- 标量、向量、矩阵和张量分别具有零、一、二和任意数量的轴;
- 一个张量可以通过sum和mean沿指定的轴降低维度;
- 两个矩阵的按元素乘法被称为他们的Hadamard积,它与矩阵乘法不同;
- 在深度学习中,我们经常使用范数,如 L 1 L_1 L1 范数、 L 2 L_2 L2 范数和Frobenius范数;
- 我们可以对标量、向量、矩阵和张量执行各种操作。
4. 微积分
在2500年前,古希腊人把一个多边形分成三角形,并把它们的面积相加,才找到计算多边形面积的方法。为了求出曲线形状(比如圆)的面积,古希腊人在这样的形状上刻内接多边形。 如下图所示,内接多边形的等长边越多,就越接近圆。 这个过程也被称为逼近法(method of exhaustion)。
事实上,逼近法就是 积分(integral calculus) 的起源。2000多年后,微积分的另一支,微分(differential calculus) 被发明出来。在微分学最重要的应用是优化问题,即考虑如何把事情做到最好,这种问题在深度学习中是无处不在的。
在深度学习中,我们“训练”模型,不断更新它们,使它们在看到越来越多的数据时变得越来越好。通常情况下,变得更好意味着最小化一个损失函数(loss function),即一个衡量“我们的模型有多糟糕”这个问题的分数。最终,我们真正关心的是生成一个模型,它能够在从未见过的数据上表现良好。但“训练”模型只能将模型与我们实际能看到的数据相拟合。 因此,我们可以将拟合模型的任务分解为两个关键问题:
优化(optimization):用模型拟合观测数据的过程;泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型。
为了帮助你在后面的章节中更好地理解优化问题和方法, 本节提供了一个非常简短的入门教程,帮你快速掌握深度学习中常用的微分知识。
%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l
4.1 导数和微分
我们首先讨论导数的计算,这是几乎所有深度学习优化算法的关键步骤。在深度学习中,我们通常选择对于模型参数可微的损失函数。简而言之,对于每个参数,如果我们把这个参数增加或减少一个无穷小的量,我们可以知道损失会以多快的速度增加或减少。
假设我们有一个函数 f : R → R f: \mathbb{R} \rightarrow \mathbb{R} f:R→R,其输入和输出都是标量。如果 f f f 的导数存在,这个极限被定义为:
f ′ ( x ) = lim h → 0 f ( x + h ) − f ( x ) h . f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}. f′(x)=h→0limhf(x+h)−f(x).如果 f ′ ( a ) f'(a) f′(a) 存在,则称 f f f 在 a a a 处是 可微(differentiable) 的。 如果 f f f 在一个区间内的每个数上都是可微的,则此函数在此区间中是可微的。我们可以将上式中的导数 f ′ ( x ) f'(x) f′(x) 解为 f ( x ) f(x) f(x) 相对于 x x x 的 瞬时(instantaneous) 变化率。所谓的瞬时变化率是基于 x x x 中的变化 h h h,且 h h h 接近 0 0 0。
为了更好地解释导数,让我们做一个实验。定义 u = f ( x ) = 3 x 2 − 4 x u=f(x)=3x^2-4x u=f(x)=3x2−4x 如下(d2l 为书中提供的代码使用其他框架时的公共库):
def f(x):
return 3 * x ** 2 - 4 * x
通过令 x = 1 x=1 x=1 并让 h h h 接近 0 0 0,上式中 f ( x + h ) − f ( x ) h \frac{f(x+h)-f(x)}{h} hf(x+h)−f(x) 的数值结果接近 2 2 2。虽然这个实验不是一个数学证明,但我们稍后会看到,当 x = 1 x=1 x=1 时,导数 u ′ u' u′ 是 2 2 2。
def numerical_lim(f, x, h):
return (f(x + h) - f(x)) / h
h = 0.1
for i in range(5):
print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
h *= 0.1
h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003
让我们熟悉一下导数的几个等价符号。给定 y = f ( x ) y=f(x) y=f(x),其中 x x x 和 y y y 分别是函数 f f f 的自变量和因变量。以下表达式是等价的:
f ′ ( x ) = y ′ = d y d x = d f d x = d d x f ( x ) = D f ( x ) = D x f ( x ) f'(x) = y' = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx} f(x) = Df(x) = D_x f(x) f′(x)=y′=dxdy=dxdf=dxdf(x)=Df(x)=Dxf(x)
其中符号 d d x \frac{d}{dx} dxd 和 D D D 是微分运算符,表示微分操作。我们可以使用以下规则来对常见函数求微分:
- d d x C = 0 \frac{d}{dx} C = 0 dxdC=0 (对于任意常数 C C C)
- d d x x n = n x n − 1 \frac{d}{dx} x^n = n x^{n-1} dxdxn=nxn−1 (对于 n ≠ 0 n\neq 0 n=0)
- d d x e x = e x \frac{d}{dx} e^x = e^x dxdex=ex
- d d x ln x = x − 1 \frac{d}{dx} \ln x = x^{-1} dxdlnx=x−1
为了微分一个由一些常见函数组成的函数,下面的一些法则方便使用。假设函数 f f f 和 g g g 都是可微的, C C C 是一个常数,则:
- 常数相乘法则: d d x [ C f ( x ) ] = C d d x f ( x ) \frac{d}{dx} [C f(x)] = C \frac{d}{dx} f(x) dxd[Cf(x)]=Cdxdf(x)
- 加法法则: d d x [ f ( x ) + g ( x ) ] = d d x f ( x ) + d d x g ( x ) \frac{d}{dx} [f(x) + g(x)] = \frac{d}{dx} f(x) + \frac{d}{dx} g(x) dxd[f(x)+g(x)]=dxdf(x)+dxdg(x)
- 乘法法则: d d x [ f ( x ) g ( x ) ] = f ( x ) d d x g ( x ) + g ( x ) d d x f ( x ) \frac{d}{dx} [f(x) g(x)] = f(x) \frac{d}{dx} g(x) + g(x) \frac{d}{dx} f(x) dxd[f(x)g(x)]=f(x)dxdg(x)+g(x)dxdf(x)
- 除法法则: d d x f ( x ) g ( x ) = g ( x ) d d x f ( x ) − f ( x ) d d x g ( x ) g 2 ( x ) \frac{d}{dx} \frac{f(x)}{g(x)} = \frac{g(x) \frac{d}{dx} f(x) - f(x) \frac{d}{dx} g(x)}{g^2(x)} dxdg(x)f(x)=g2(x)g(x)dxdf(x)−f(x)dxdg(x)
现在我们可以应用上述几个法则来计算 u ′ = f ′ ( x ) = 3 d d x x 2 − 4 d d x x = 6 x − 4 u'=f'(x)=3\frac{d}{dx}x^2-4\frac{d}{dx}x=6x-4 u′=f′(x)=3dxdx2−4dxdx=6x−4。令 x = 1 x=1 x=1,我们有 u ′ = 2 u'=2 u′=2:在这个实验中,数值结果接近 2 2 2,这一点得到了我们在本节前面的实验的支持。 当 x = 1 x=1 x=1 时,此导数也是曲线 u = f ( x ) u=f(x) u=f(x) 切线的斜率。
4.2 可视化工具
为了对导数的这种解释进行可视化,我们将使用 matplotlib, 这是一个 Python 中流行的绘图库。要配置 matplotlib 生成图形的属性,我们需要定义几个函数。在下面,use_svg_display 函数指定 matplotlib 软件包输出 svg 图表以获得更清晰的图像(svg:可缩放矢量图形文件)。
注意,注释 #@save 是一个特殊的标记,会将对应的函数、类或语句保存在d2l包中(这些是封装进d2l包中的函数,这里只是做个标记)。因此,以后无须重新定义就可以直接调用它们,也就是直接调用 d2l.use_svg_display()。
def use_svg_display(): #@save
"""使用svg格式在Jupyter中显示绘图"""
backend_inline.set_matplotlib_formats('svg')
方便的是,我们可以使用 set_figsize 来设置图形大小。由于在 d2l 包中通过 #@save 标记了 from matplotlib import pyplot as plt 的导入语句,我们可以调用 d2l.plt。
def set_figsize(figsize=(3.5, 2.5)): #@save
"""设置matplotlib的图表大小"""
use_svg_display()
d2l.plt.rcParams['figure.figsize'] = figsize
下面的 set_axes 函数用于设置由 matplotlib 生成图表的轴的属性。
#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
"""设置matplotlib的轴"""
axes.set_xlabel(xlabel)
axes.set_ylabel(ylabel)
axes.set_xscale(xscale)
axes.set_yscale(yscale)
axes.set_xlim(xlim)
axes.set_ylim(ylim)
if legend:
axes.legend(legend)
axes.grid()
通过这三个用于图形配置的函数,我们定义了 plot 函数来简洁地绘制多条曲线,因为我们需要在整个书中可视化许多曲线。
#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
ylim=None, xscale='linear', yscale='linear',
fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
"""绘制数据点"""
if legend is None:
legend = []
set_figsize(figsize)
axes = axes if axes else d2l.plt.gca()
# 如果X有一个轴,输出True
def has_one_axis(X):
return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
and not hasattr(X[0], "__len__"))
if has_one_axis(X):
X = [X]
if Y is None:
X, Y = [[]] * len(X), X
elif has_one_axis(Y):
Y = [Y]
if len(X) != len(Y):
X = X * len(Y)
axes.cla()
for x, y, fmt in zip(X, Y, fmts):
if len(x):
axes.plot(x, y, fmt)
else:
axes.plot(y, fmt)
set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
现在我们可以绘制函数 u = f ( x ) u=f(x) u=f(x) 及其在 x = 1 x=1 x=1 处的切线 y = 2 x − 3 y=2x-3 y=2x−3, 其中系数 2 2 2 是切线的斜率。
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

4.3 偏导数
到目前为止,我们只讨论了仅含一个变量的函数的微分。在深度学习中,函数通常依赖于许多变量。 因此,我们需要将微分的思想推广到 多元函数(multivariate function) 上。
设 y = f ( x 1 , x 2 , … , x n ) y = f(x_1, x_2, \ldots, x_n) y=f(x1,x2,…,xn) 是一个具有 n n n 个变量的函数。 y y y 关于第 i i i 个参数 x i x_i xi 的 偏导数(partial derivative)为:
∂ y ∂ x i = lim h → 0 f ( x 1 , … , x i − 1 , x i + h , x i + 1 , … , x n ) − f ( x 1 , … , x i , … , x n ) h \frac{\partial y}{\partial x_i} = \lim_{h \rightarrow 0} \frac{f(x_1, \ldots, x_{i-1}, x_i+h, x_{i+1}, \ldots, x_n) - f(x_1, \ldots, x_i, \ldots, x_n)}{h} ∂xi∂y=h→0limhf(x1,…,xi−1,xi+h,xi+1,…,xn)−f(x1,…,xi,…,xn)
为了计算 ∂ y ∂ x i \frac{\partial y}{\partial x_i} ∂xi∂y,我们可以简单地将 x 1 , … , x i − 1 , x i + 1 , … , x n x_1, \ldots, x_{i-1}, x_{i+1}, \ldots, x_n x1,…,xi−1,xi+1,…,xn 看作常数,并计算 y y y 关于 x i x_i xi 的导数。对于偏导数的表示,以下是等价的:
∂ y ∂ x i = ∂ f ∂ x i = ∂ x i f = ∂ i f = f x i = f i = D i f = D x i f . \frac{\partial y}{\partial x_i} = \frac{\partial f}{\partial x_i} = \partial_{x_i} f = \partial_i f = f_{x_i} = f_i = D_i f = D_{x_i} f. ∂xi∂y=∂xi∂f=∂xif=∂if=fxi=fi=Dif=Dxif.
4.4 梯度
我们可以连结一个多元函数对其所有变量的 偏导数,以得到该函数的梯度(gradient)向量。具体而言,设函数 f : R n → R f:\mathbb{R}^n\rightarrow\mathbb{R} f:Rn→R 的输入是一个 n n n 维向量 x = [ x 1 , x 2 , … , x n ] ⊤ \mathbf{x}=[x_1,x_2,\ldots,x_n]^\top x=[x1,x2,…,xn]⊤,并且输出是一个标量。函数 f ( x ) f(\mathbf{x}) f(x) 相对于 x \mathbf{x} x 的梯度是一个包含 n n n 个偏导数的向量(包含 n n n维向量所有 n n n个偏导数的向量为梯度):
∇ x f ( x ) = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , … , ∂ f ( x ) ∂ x n ] ⊤ \nabla_{\mathbf{x}} f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_n}\bigg]^\top ∇xf(x)=[∂x1∂f(x),∂x2∂f(x),…,∂xn∂f(x)]⊤
其中 ∇ x f ( x ) \nabla_{\mathbf{x}} f(\mathbf{x}) ∇xf(x) 通常在没有歧义时被 ∇ f ( x ) \nabla f(\mathbf{x}) ∇f(x) 取代。
假设 x \mathbf{x} x 为 n n n 维向量,在微分多元函数时经常使用以下规则:
- 对于所有 A ∈ R m × n \mathbf{A} \in \mathbb{R}^{m \times n} A∈Rm×n,都有 ∇ x A x = A ⊤ \nabla_{\mathbf{x}} \mathbf{A} \mathbf{x} = \mathbf{A}^\top ∇xAx=A⊤;
- 对于所有 A ∈ R n × m \mathbf{A} \in \mathbb{R}^{n \times m} A∈Rn×m,都有 ∇ x x ⊤ A = A \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A} = \mathbf{A} ∇xx⊤A=A;
- 对于所有 A ∈ R n × n \mathbf{A} \in \mathbb{R}^{n \times n} A∈Rn×n,都有 ∇ x x ⊤ A x = ( A + A ⊤ ) x \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{A} \mathbf{x} = (\mathbf{A} + \mathbf{A}^\top)\mathbf{x} ∇xx⊤Ax=(A+A⊤)x;
- ∇ x ∥ x ∥ 2 = ∇ x x ⊤ x = 2 x \nabla_{\mathbf{x}} \|\mathbf{x} \|^2 = \nabla_{\mathbf{x}} \mathbf{x}^\top \mathbf{x} = 2\mathbf{x} ∇x∥x∥2=∇xx⊤x=2x。
同样,对于任何矩阵 X \mathbf{X} X,都有 ∇ X ∥ X ∥ F 2 = 2 X \nabla_{\mathbf{X}} \|\mathbf{X} \|_F^2 = 2\mathbf{X} ∇X∥X∥F2=2X。正如我们之后将看到的,梯度对于设计深度学习中的优化算法有很大用处。
4.5 链式法则
然而,上面方法可能很难找到梯度----这是因为在深度学习中,多元函数通常是 复合(composite) 的, 所以我们可能没法应用上述任何规则来微分这些函数。幸运的是,链式法则 使我们能够微分复合函数。
让我们先考虑单变量函数。假设函数 y = f ( u ) y=f(u) y=f(u) 和 u = g ( x ) u=g(x) u=g(x) 都是可微的,根据链式法则:
d y d x = d y d u d u d x \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx} dxdy=dudydxdu回到多元函数,假设 y = f ( u ) y = f(\mathbf{u}) y=f(u) 有变量 u 1 , u 2 , … , u m u_1, u_2, \ldots, u_m u1,u2,…,um,其中每个 u i = g i ( x ) u_i = g_i(\mathbf{x}) ui=gi(x) 有变量 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn,即 u = g ( x ) \mathbf{u} = g(\mathbf{x}) u=g(x)。那么链式法规定:
∂ y ∂ x i = ∂ y ∂ u 1 ∂ u 1 ∂ x i + ∂ y ∂ u 2 ∂ u 2 ∂ x i + … + ∂ y ∂ u m ∂ u m ∂ x i \frac{\partial y}{\partial x_i} = \frac{\partial y}{\partial u_1} \frac{\partial u_1}{\partial x_i} + \frac{\partial y}{\partial u_2} \frac{\partial u_2}{\partial x_i} + \ldots + \frac{\partial y}{\partial u_m} \frac{\partial u_m}{\partial x_i} ∂xi∂y=∂u1∂y∂xi∂u1+∂u2∂y∂xi∂u2+…+∂um∂y∂xi∂um这样:
∇ x y = A ∇ u y \nabla_{\mathbf{x}} y = \mathbf{A} \nabla_{\mathbf{u}} y ∇xy=A∇uy其中 A ∈ R n × m \mathbf{A} \in \mathbb{R}^{n \times m} A∈Rn×m 是一个矩阵,包含向量 u \mathbf{u} u 相对于向量 x \mathbf{x} x 的导数。因此,计算梯度需要计算一个向量-矩阵乘积。这就是为什么线性代数是构建深度学习系统的一个关键基础的原因之一。
4.6 小结
- 微分和积分是微积分的两个分支,前者可以应用于深度学习中的优化问题;
- 导数可以被解释为函数相对于其变量的瞬时变化率,它也是函数曲线的切线的斜率;
- 梯度是一个向量,其分量是多变量函数相对于其所有变量的偏导数;
- 链式法则使我们能够微分复合函数。
5. 自动微分(Important)
正如我们在前面所说的那样,求导是几乎所有深度学习优化算法的关键步骤。虽然求导的计算很简单,只需要一些基本的微积分。但对于复杂的模型,手工进行更新是一件很痛苦的事情(而且经常容易出错)。
幸运的是,所有现代深度学习框架都通过提供 自动微分(automatic differentiation) 来为我们减轻这项工作负担。当我们将数据传递给每个连续的函数时,框架会构建一个 计算图(computational graph),该图跟踪每个值如何依赖于其他值。为了计算导数,自动微分会逆向遍历这个图并应用链式法则。以这种方式应用链式法则的计算算法被称为 反向传播(back-propagate)。
import torch
5.1. 一个简单的例子
作为一个演示例子,假设我们想对函数 y = 2 x ⊤ x y=2\mathbf{x}^{\top}\mathbf{x} y=2x⊤x 关于 列向量 x \mathbf{x} x 求导。首先,我们创建变量 x \mathbf{x} x 并为其分配一个初始值。
x = torch.arange(4.0)
x
tensor([0., 1., 2., 3.])
在我们计算 y y y 关于 x \mathbf{x} x 的梯度之前,我们需要一个地方来存储梯度。重要的是,我们不会在每次对一个参数求导时都分配新的内存。因为我们经常会成千上万次地更新相同的参数,每次都分配新的内存可能很快就会将内存耗尽。注意,一个标量函数关于向量 x \mathbf{x} x 的梯度是向量,并且与 x \mathbf{x} x 具有相同的形状。(也就是说,设置.requires_grad_(True)会额外开辟一块内存,每次参数求导时,结果就会更新在这里)
x.requires_grad_(True) # 等价于x=torch.arange(4.0,requires_grad=True)
##上面额输出tensor([0., 1., 2., 3.], requires_grad=True)
x.grad # 默认值是None
我们现在计算关于 x x x 的函数,并将结果赋值给 y y y。
y = 2 * torch.dot(x, x)
y
tensor(28., grad_fn=<MulBackward0>)
x \mathbf{x} x 是一个长度为 4 4 4 的向量,计算 x \mathbf{x} x 和 x \mathbf{x} x 的点积,得到了赋值给 y 的标量输出。接下来,通过调用 反向传播函数 来自动计算 y 关于 x \mathbf{x} x 每个分量的梯度,并打印这些梯度。(这时候调用了反向传播函数.backward(),才更新了梯度结果)
y.backward()
x.grad
tensor([ 0., 4., 8., 12.])
函数 y = 2 x ⊤ x y=2\mathbf{x}^{\top}\mathbf{x} y=2x⊤x 关于 x \mathbf{x} x 的梯度应为 4 x 4\mathbf{x} 4x。 让我们快速验证这个梯度是否计算正确:
x.grad == 4 * x
tensor([True, True, True, True])
现在让我们计算 x 的另一个函数并求其梯度。注意,当我们记录一个新的梯度时,PyTorch 不会自动重置梯度缓冲区。相反,新的梯度会被加到已经存储的梯度上。这种行为在我们想要优化多个目标函数之和时非常有用。要重置梯度缓冲区,我们可以调用 x.grad.zero_(),如下所示:(如果不使用 x.grad.zero_(),重复计算 y = 2 * torch.dot(x, x) 并运行 y.backward(),第二次得到的 x.grad 会变成 tensor([ 0., 8., 16., 24.]))。
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
tensor([1., 1., 1., 1.])
5.2. 非标量变量的反向传播
当 y y y 是一个向量时, y y y 对向量 x x x 的导数的最自然表示是一个称为 雅可比矩阵 的矩阵,它包含了 y y y 的每个分量对 x x x 的每个分量的偏导数。同样地,对于更高阶的 y y y 和 x x x,微分的结果可能是一个更高阶的张量。
虽然雅可比矩阵在一些高级的机器学习技术中确实会出现,但更常见的是,我们希望将 y y y 的每个分量对整个向量 x x x 的梯度求和,从而得到一个与 x x x 形状相同的向量。例如,我们通常有一个向量,表示为一批训练样本中每个样本单独计算的损失函数值。在这里,我们只需要将为每个样本单独计算的梯度求和即可。(分量的话使用上面的方式就可以得到了,批量则使用这种方式)
因为深度学习框架在解释 非标量张量 的梯度时存在差异,PyTorch 采取了一些措施来避免混淆。对一个 非标量 调用 backward 会引发错误(避免混淆!),除非我们告诉 PyTorch 如何将该对象简化为一个标量。更正式地说,我们需要提供一个向量 v \mathbf{v} v,这样 backward 将计算 v T ∂ x y \mathbf{v}^T \partial_{\mathbf{x}}\mathbf{y} vT∂xy 而不是 ∂ x y \partial_{\mathbf{x}}\mathbf{y} ∂xy。接下来的部分可能会让人感到困惑,但原因稍后会变得清晰,这个参数(代表 v \mathbf{v} v)被命名为 gradient。(这里的操作也就是定义了一个 [ 1 , 1 , 1 , 1 ] ∈ R 1 × 4 [1, 1, 1, 1]\in \mathbb{R}^{1\times4} [1,1,1,1]∈R1×4 的矩阵与原来的偏导数相乘,这样就能得到一个标量了!)
# 对非标量调用backward需要传入一个gradient参数,该参数指定微分函数关于self的梯度。
# 在我们的例子中,我们只想求偏导数的和,所以传递一个1的梯度(sum)是合适的
x.grad.zero_()
y = x * x # 按元素乘法,得到 tensor([0., 1., 4., 9.]),如果用 y = torch.dot(x, x),得 tensor(14.)
y.backward(gradient=torch.ones(len(y))) # Faster: y.sum().backward()
x.grad
tensor([0., 2., 4., 6.])
5.3. 分离计算
有时,我们希望将一些计算移出记录的 计算图 之外。例如,假设我们使用输入来创建一些我们不希望计算梯度的辅助中间项。在这种情况下,我们需要将相应的计算图从最终结果中分离出来。
下面的一个简单示例使这一点更清楚:假设我们有 z = x × y z = x \times y z=x×y 和 y = x × x y = x \times x y=x×x,但我们希望关注 x x x 对 z z z 的直接影响,而不是通过 y y y 传递的影响。在这种情况下,我们可以创建一个新的变量 u u u,它与 y y y 有相同的值,但其来源(它是如何被创建的)已被清除。这时, u u u 在图中没有祖先,梯度不会通过 u u u 传递到 x x x。例如,计算 z = x × u z = x \times u z=x×u 的梯度将得到结果 u u u,而不是你可能预期的 3 × x × x 3 \times x \times x 3×x×x,因为 z = x × x × x z = x \times x \times x z=x×x×x。(detach():将 variable 参数从网络中隔离开,不参与参数更新)
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u # 对 u*x 求导只剩 x 了
tensor([True, True, True, True])
由于记录了 y y y 的计算结果,我们可以随后在 y y y 上调用 反向传播, 得到 y = x ∗ x y=x*x y=x∗x 关于的 x x x 的导数,即 2 ∗ x 2*x 2∗x。
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x
tensor([True, True, True, True])
5.4. Python控制流的梯度计算
到目前为止,我们已经回顾了一些案例,其中输入到输出的路径是通过一个函数明确定义的,例如 z = x × x × x z = x \times x \times x z=x×x×x。编程为我们提供了更多的自由度来计算结果。例如,我们可以使结果依赖于辅助变量,或者根据中间结果进行条件选择。使用自动微分的一个好处是:即使构建函数的 计算图 需要通过 Python 控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到变量的梯度。在下面的代码中,while 循环的迭代次数和 if 语句的结果都取决于输入 a 的值。为了说明这一点,请考虑以下代码片段,其中 while 循环的迭代次数和 if 语句的评估都取决于输入 a a a 的值。
def f(a):
b = a * 2
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
下面,我们调用这个函数,传入一个随机值作为输入。由于输入是一个随机变量,我们不知道计算图会呈现什么形式。然而,每当我们对特定输入执行 f ( a ) f(a) f(a) 时,我们就会实现一个特定的计算图,并可以随后进行反向传播。
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
尽管为了演示的目的,我们的函数 f f f 有些不自然或不真实,但其对输入的依赖关系却相当简单:它是关于 a a a 的线性函数,并且具有分段定义的尺度(即在不同的区间内有不同的线性关系)。因此, f ( a ) / a f(a) / a f(a)/a 是一个常数向量,并且更重要的是, f ( a ) / a f(a) / a f(a)/a 需要与 f ( a ) f(a) f(a) 相对于 a a a 的梯度相匹配.
a.grad == d / a
tensor(True)
在深度学习中,动态控制流 非常常见。例如,在处理文本时,计算图依赖于输入的长度。在这种情况下,自动微分对于统计建模至关重要,因为不可能预先计算梯度。
5.5. 小结
- 深度学习框架可以自动计算导数:我们首先将梯度附加到想要对其计算偏导数的变量上。然后我们记录目标值的计算,执行它的反向传播函数,并访问得到的梯度。
6. 概率与统计学
无论如何,机器学习都与不确定性息息相关。在有监督学习中,我们希望根据已知的事物(特征(feature))预测未知的事物(目标(target))。根据我们的目标,我们可能会尝试预测目标最有可能的值。或者我们可能会预测与目标预期距离最小的值。有时我们不仅希望预测一个特定的值,还希望量化我们的不确定性。例如,给定描述患者的一些特征,我们可能想知道他们在明年患心脏病的可能性有多大。在无监督学习中,我们经常关心不确定性。要确定一组测量值是否异常,了解在感兴趣的总体中观察到这些值的可能性有多大会很有帮助。此外,在强化学习中,我们希望开发在各种环境中智能行动的智能体。这需要推理环境可能如何变化以及针对每个可用动作可能会遇到哪些奖励。
概率(Probability) 是涉及不确定性推理的数学领域。给定某个过程的概率模型,我们可以推断各种事件的可能性。使用概率来描述可重复事件(如抛硬币)的频率是相当没有争议的。事实上,频率主义者学者坚持一种仅适用于此类可重复事件的概率解释。
相比之下,贝叶斯学者更广泛地使用概率语言来形式化不确定性下的推理。贝叶斯概率具有两个独特的特征:
- 为不可重复事件分配置信度,例如,大坝坍塌的概率是多少?;
- 主观性。虽然贝叶斯概率为人们应如何根据新证据更新其信念提供了明确的规则,但它允许不同的个体从不同的先验信念开始。
统计学帮助我们进行逆向推理,从收集和组织数据开始,然后推断出我们可能对生成数据的过程得出的结论。每当我们分析一个数据集,寻找我们希望能够表征更广泛人群的模式时,我们都在运用统计思维。许多课程、专业、论文、职业、部门、公司和机构都致力于概率和统计学的研究。虽然本节只是触及皮毛,但我们将提供你开始构建模型所需的基础。
%matplotlib inline
import random
import torch
from torch.distributions.multinomial import Multinomial
from d2l import torch as d2l
6.1 一个简单示例:抛硬币
假设我们计划抛一枚硬币,并想量化看到正面(相对于反面)的可能性有多大。如果硬币是公平的,那么两种结果(正面和反面)的可能性是相等的。此外,如果我们计划抛硬币 n n n 次,那么我们期望看到的正面次数的比例应该与期望的反面次数的比例完全相同。一种直观的理解方式是通过对称性:对于每一个可能的结果,有 n h n_h nh 次正面和 n t = ( n − n h ) n_\textrm{t} = (n - n_\textrm{h}) nt=(n−nh) 次反面,就有一个同样可能的结果,有 n t n_t nt 次正面和 n h n_h nh 次反面。请注意,只有当我们平均期望看到一半的抛掷结果是正面,一半是反面时,这才是可能的。当然,如果你多次进行这个实验,每次抛掷 n = 1000000 n=1000000 n=1000000 次,你可能永远不会看到一次试验中正面次数 n h n_h nh 正好等于反面次数 n t n_t nt。
形式上,数量 1 / 2 1/2 1/2 被称为 概率,在这里它捕捉到任何一次抛掷出现正面的确定性。概率将 0 到 1 之间的分数分配给感兴趣的结果,称为 事件(event)。这里感兴趣的事件是正面,我们用相应的概率P(正面)表示。概率为 1 表示绝对确定性(想象一枚两面都是正面的魔术硬币),概率为 0 表示不可能(例如,如果两面都是反面)。频率 n h / n n_\textrm{h}/n nh/n 和 n t / n n_\textrm{t}/n nt/n 不是概率,而是 统计量(statistics)。概率是理论上的量,它是数据生成过程的基础。在这里,概率 1/2 是硬币本身的一个属性。相比之下,统计量是 经验性(empirical) 的量,它是作为观察数据的函数计算出来的。我们对 概率量 和 统计量 的兴趣是紧密交织在一起的。我们经常设计一种特殊的统计量,称为 估计量(estimator),给定一个数据集,它会产生模型参数(如概率)的估计值。此外,当这些估计量满足一个称为 一致性(consistency) 的良好属性时,我们的估计值将收敛到相应的概率。反过来,这些推断出的概率告诉我们未来可能遇到的来自同一总体的数据的可能统计特性。
假设我们偶然发现一枚真正的硬币,但我们不知道其真实的P(正面)。要用统计方法研究这个量,我们需要:
- 收集一些数据;
- 设计一个估计量。
这里的数据采集很容易;我们可以多次抛硬币并记录所有的结果。形式上,从某个潜在的随机过程中抽取实现结果被称为 抽样(sampling)。正如你可能猜到的,一个自然的估计量是观察到的正面次数与抛掷总次数的比例。
现在,假设硬币实际上是公平的,即 P ( heads ) = 0.5 P(\textrm{heads}) = 0.5 P(heads)=0.5。为了模拟公平硬币的抛掷,我们可以调用任何随机数生成器。有一些简单的方法可以抽取概率为 0.5 的事件的样本。例如,Python 的 random.random 在区间[0,1]中生成数字,其中落在任何子区间 [ a , b ] ⊂ [ 0 , 1 ] [a, b] \subset [0,1] [a,b]⊂[0,1] 的概率等于 b − a b-a b−a。因此,通过测试返回的浮点数是否大于 0.5 0.5 0.5,我们可以以概率 0.5 0.5 0.5 得到 0 0 0 和 1 1 1:
num_tosses = 100
heads = sum([random.random() > 0.5 for _ in range(num_tosses)])
tails = num_tosses - heads
print("heads, tails: ", [heads, tails])
heads, tails: [44, 56]
更一般地,我们可以通过调用多项分布函数来模拟从具有有限个可能结果的任何变量中进行多次抽取(就像抛硬币或掷骰子一样),将第一个参数设置为抽取次数,第二个参数设置为与每个可能结果相关联的概率列表。为了模拟公平硬币的十次抛掷,我们分配概率向量[0.5, 0.5],将索引 0 解释为正面,索引 1 解释为反面。该函数返回一个长度等于可能结果数量的向量(这里是 2),其中第一个分量告诉我们正面出现的次数,第二个分量告诉我们反面出现的次数。
fair_probs = torch.tensor([0.5, 0.5])
Multinomial(100, fair_probs).sample()
tensor([50., 50.])
每次运行此采样过程,你都会收到一个新的随机值,该值可能与之前的结果不同。除以投掷次数,我们就得到了数据中每个结果的频率。请注意,这些频率就像它们旨在估计的概率一样,总和为 1。
Multinomial(100, fair_probs).sample() / 100
tensor([0.4800, 0.5200])
在这里,尽管我们模拟的硬币是公平的(我们自己设定了概率[0.5, 0.5]),但正面和反面的计数可能并不相同。这是因为我们只抽取了相对较少的样本。如果我们自己不进行模拟,而只看到结果,我们怎么知道硬币是否稍微不公平,或者与 1 / 2 1/2 1/2 的可能偏差是否只是小样本量的假象呢?让我们看看当我们模拟 10000 次投掷时会发生什么。
counts = Multinomial(10000, fair_probs).sample()
counts / 10000
tensor([0.4966, 0.5034])
一般来说,对于重复事件的平均值(如抛硬币),随着重复次数的增加,我们的估计值一定会收敛到真实的潜在概率。这种现象的数学公式被称为 大数定律(law of large numbers),并且中心极限定理告诉我们,在许多情况下,随着样本大小 n n n 的增加,这些误差应该以( ( 1 / n ) (1/\sqrt{n}) (1/n))的速率下降。让我们通过研究当我们将抛硬币的次数从 1 增加到 10000 时我们的估计值是如何演变的,来获得更多的直觉。
counts = Multinomial(1, fair_probs).sample((10000,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)
estimates = estimates.numpy()
d2l.set_figsize((4.5, 3.5))
d2l.plt.plot(estimates[:, 0], label=("P(coin=heads)"))
d2l.plt.plot(estimates[:, 1], label=("P(coin=tails)"))
d2l.plt.axhline(y=0.5, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Samples')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();
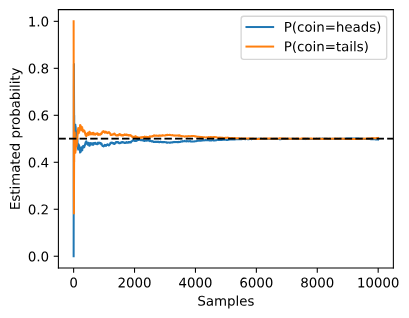
每条实线曲线对应硬币的两个值之一,并给出了在每组实验后硬币出现该值的估计概率。虚线黑线给出了真实的潜在概率。随着我们通过进行更多实验获得更多数据,曲线会趋向于真实概率。你可能已经开始看到一些让统计学家全神贯注的更高级问题的轮廓:这种收敛发生得有多快?如果我们已经测试了同一工厂生产的许多硬币,我们如何整合这些信息?
6.2 一种更正式的处理方法
我们已经取得了很大的进展:提出概率模型、生成合成数据、运行统计估计器、实证评估收敛性并报告误差指标(检查偏差)。然而,要更进一步,我们需要更加精确。
在处理随机性时,我们用符号 S \mathcal{S} S 表示可能结果的集合,并称之为样本空间或结果空间。在这里,每个元素都是一个不同的可能结果。例如,掷一枚硬币时, S = { heads , tails } \mathcal{S} = \{\textrm{heads}, \textrm{tails}\} S={heads,tails}。掷一个骰子时, S = { 1 , 2 , 3 , 4 , 5 , 6 } \mathcal{S} = \{1, 2, 3, 4, 5, 6\} S={1,2,3,4,5,6}。掷两枚硬币时,可能的结果是 { ( heads , heads ) , ( heads , tails ) , ( tails , heads ) , ( tails , tails ) } \{(\textrm{heads}, \textrm{heads}), (\textrm{heads}, \textrm{tails}), (\textrm{tails}, \textrm{heads}), (\textrm{tails}, \textrm{tails})\} {(heads,heads),(heads,tails),(tails,heads),(tails,tails)}。事件是样本空间的子集。例如,“第一次掷硬币出现正面”这个事件对应于集合 { ( heads , heads ) , ( heads , tails ) } \{(\textrm{heads}, \textrm{heads}), (\textrm{heads}, \textrm{tails})\} {(heads,heads),(heads,tails)}。当随机实验的结果 z z z 满足 z ∈ A z \in \mathcal{A} z∈A 时,那么事件 A \mathcal{A} A 就发生了。对于掷一次骰子,我们可以定义事件“看到 5”( A = { 5 } \mathcal{A} = \{5\} A={5})和“看到奇数”( B = { 1 , 3 , 5 } \mathcal{B} = \{1, 3, 5\} B={1,3,5})。在这种情况下,如果骰子出现 5,我们会说事件 A \mathcal{A} A 和 B \mathcal{B} B 都发生了。另一方面,如果 z = 3 z = 3 z=3,那么事件 A \mathcal{A} A 没有发生但事件 B \mathcal{B} B 发生了。
一个概率函数将事件映射到实数值 P : A ⊆ S → [ 0 , 1 ] {P: \mathcal{A} \subseteq \mathcal{S} \rightarrow [0,1]} P:A⊆S→[0,1]。在给定样本空间 S \mathcal{S} S 中事件 A \mathcal{A} A 的概率,记为 P ( A ) P(\mathcal{A}) P(A),具有以下性质:
- 任何事件 P ( A ) P(\mathcal{A}) P(A) 的概率都是非负实数,即 P ( A ) ≥ 0 P(\mathcal{A}) \geq 0 P(A)≥0;
- 整个样本空间的概率是 1,即: P ( S ) = 1 P(\mathcal{S}) = 1 P(S)=1;
- 对于任何可数序列的事件 A 1 , A 2 , … \mathcal{A}_1, \mathcal{A}_2, \ldots A1,A2,…,如果它们是
互斥(mutually exclusive)的(即对于所有 i ≠ j i\neq j i=j, A i ∩ A j = ∅ \mathcal{A}_i \cap \mathcal{A}_j = \emptyset Ai∩Aj=∅),那么其中任何一个事件发生的概率等于它们各自概率的和,即 P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup_{i=1}^{\infty} \mathcal{A}_i) = \sum_{i=1}^{\infty} P(\mathcal{A}_i) P(⋃i=1∞Ai)=∑i=1∞P(Ai)。
这些由柯尔莫哥洛夫(1933)提出的概率论公理可以迅速推导出许多重要的结论。例如,立即可以得出任何事件 A \mathcal{A} A 或其补事件 A ′ \mathcal{A}' A′ 发生的概率是 1(因为 A ∪ A ′ = S \mathcal{A} \cup \mathcal{A}' = \mathcal{S} A∪A′=S)。我们也可以证明 P ( ∅ ) = 0 P(\emptyset) = 0 P(∅)=0,因为 1 = P ( S ∪ S ′ ) = P ( S ∪ ∅ ) = P ( S ) + P ( ∅ ) = 1 + P ( ∅ ) 1 = P(\mathcal{S} \cup \mathcal{S}') = P(\mathcal{S} \cup \emptyset) = P(\mathcal{S}) + P(\emptyset) = 1 + P(\emptyset) 1=P(S∪S′)=P(S∪∅)=P(S)+P(∅)=1+P(∅)。因此,任何事件 A \mathcal{A} A 和其补事件 A ′ \mathcal{A}' A′ 同时发生的概率是 P ( A ∩ A ′ ) = 0 P(\mathcal{A} \cap \mathcal{A}') = 0 P(A∩A′)=0。通俗地说,这告诉我们不可能事件发生的概率为零。
6.1.1. 概率论公理
在处理骰子掷出时,我们将集合 S = { 1 , 2 , 3 , 4 , 5 , 6 } \mathcal{S}= \{1, 2, 3, 4, 5, 6\} S={1,2,3,4,5,6} 称为 样本空间(sample space) 或 结果空间(outcome space),其中每个元素都是结果(outcome)。事件(event) 是一组给定样本空间的随机结果。例如,“看到 5 5 5” ( { 5 } ) (\{5\}) ({5})和“看到奇数” ( { 1 , 3 , 5 } ) (\{1, 3, 5\}) ({1,3,5})都是掷出骰子的有效事件。注意,如果一个随机实验的结果在 A \mathcal{A} A 中,则事件 A \mathcal{A} A 已经发生。也就是说,如果投掷出 3 3 3点,因为 3 ∈ { 1 , 3 , 5 } 3 \in \{1, 3, 5\} 3∈{1,3,5},我们可以说,“看到奇数”的事件发生了。
概率(probability)可以被认为是将集合映射到真实值的函数。在给定的样本空间 S \mathcal{S} S 中,事件 A \mathcal{A} A 的概率,表示为 P ( A ) P(\mathcal{A}) P(A),满足以下属性:
- 对于任意事件 A \mathcal{A} A,其概率从不会是负数,即 P ( A ) ≥ 0 P(\mathcal{A}) \geq 0 P(A)≥0;
- 整个样本空间的概率为 1 1 1,即 P ( S ) = 1 P(\mathcal{S}) = 1 P(S)=1;
- 对于
互斥(mutually exclusive)事件(对于所有 i ≠ j i \neq j i=j 都有 A i ∩ A j = ∅ \mathcal{A}_i \cap \mathcal{A}_j = \emptyset Ai∩Aj=∅)的任意一个可数序列 A 1 , A 2 , … \mathcal{A}_1, \mathcal{A}_2, \ldots A1,A2,…,序列中任意一个事件发生的概率等于它们各自发生的概率之和,即: P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup_{i=1}^{\infty} \mathcal{A}_i) = \sum_{i=1}^{\infty} P(\mathcal{A}_i) P(⋃i=1∞Ai)=∑i=1∞P(Ai)。
以上也是概率论的公理,由科尔莫戈罗夫于1933年提出。有了这个公理系统,我们可以避免任何关于随机性的哲学争论;相反,我们可以用数学语言严格地推理。例如,假设事件 A 1 \mathcal{A}_1 A1 为整个样本空间,且当所有 i > 1 i > 1 i>1 时的 A i = ∅ \mathcal{A}_i = \emptyset Ai=∅, 那么我们可以证明 P ( ∅ ) = 0 P(\emptyset) = 0 P(∅)=0,即不可能发生事件的概率是 0 0 0。
6.3 随机变量
当我们谈到诸如掷骰子出现奇数或第一次抛硬币出现正面这样的事件时,我们引入了 随机变量(random variable) 的概念。形式上,随机变量是从一个潜在样本空间到一组(可能有很多)值的映射。你可能会想随机变量与样本空间有何不同,因为两者都是结果的集合。重要的是,随机变量可能比原始样本空间粗糙得多。即使潜在样本空间是无限的,例如在 0 和 1 之间的线段上的点,我们也可以定义一个二元随机变量,如“大于 0.5”。此外,多个随机变量可以共享相同的潜在样本空间。例如,“我的家庭警报是否响起”和“我的房子是否被盗”都是二元随机变量,它们共享一个潜在样本空间。因此,知道一个随机变量所取的值可以告诉我们另一个随机变量可能的值。知道警报响起,我们可能会怀疑房子很可能被盗了。
随机变量取的每个值都对应于潜在样本空间的一个子集。因此,随机变量 X X X 取值为 v v v 的情况,用 X = v X=v X=v 表示,是一个事件, P ( X = v ) P(X=v) P(X=v) 表示其概率。有时这种表示法可能会很笨拙,在上下文清楚的情况下我们可以滥用表示法。例如,我们可以用 P ( X ) P(X) P(X) 来广泛地指代 X X X 的 分布(distribution),即告诉我们 X X X 取任何给定值的概率的函数。其他时候,我们写出像 P ( X , Y ) = P ( X ) P ( Y ) P(X,Y) = P(X) P(Y) P(X,Y)=P(X)P(Y) 这样的表达式,作为一种简写,来表达对于随机变量 X X X 和 Y Y Y 可以取的所有值都成立的陈述,即对于所有的 i i i, j j j,都有 P ( X = i and Y = j ) = P ( X = i ) P ( Y = j ) P(X=i \textrm{ and } Y=j) = P(X=i)P(Y=j) P(X=i and Y=j)=P(X=i)P(Y=j)。其他时候,当随机变量从上下文很清楚时,我们滥用表示法,写成 P ( v ) P(v) P(v)。由于概率论中的事件是样本空间中的一组结果,我们可以指定随机变量取的值的范围。例如, P ( 1 ≤ X ≤ 3 ) P(1 \leq X \leq 3) P(1≤X≤3) 表示事件 { 1 ≤ X ≤ 3 } \{1 \leq X \leq 3\} {1≤X≤3} 的概率。
请注意,离散随机变量(如抛硬币或掷骰子)与连续随机变量(如从人群中随机抽取的人的体重和身高)之间有细微的差别。在这种情况下,我们很少真正关心某人的确切身高。此外,如果我们进行足够精确的测量,我们会发现地球上没有两个人的身高完全相同。实际上,用足够精细的测量,你在醒来时和睡觉时的身高永远不会相同。询问某人确切身高为 1.801392782910287192 米的概率没有什么意义。相反,我们通常更关心能够说出某人的身高是否落在给定区间内,例如在 1.79 米和 1.81 米之间。在这些情况下,我们使用概率密度(probability density)。正好 1.80 米的身高没有概率,但有非零密度。要计算分配给一个区间的概率,我们必须对该区间上的密度进行积分。
6.2. 处理多个随机变量
很多时候,我们会考虑多个随机变量。比如,我们可能需要对疾病和症状之间的关系进行建模。给定一个疾病和一个症状,比如“流感”和“咳嗽”,以某个概率存在或不存在于某个患者身上。我们需要估计这些概率以及概率之间的关系,以便我们可以运用我们的推断来实现更好的医疗服务。
再举一个更复杂的例子:图像包含数百万像素,因此有数百万个随机变量。在许多情况下,图像会附带一个标签(label),标识图像中的对象。我们也可以将标签视为一个随机变量。我们甚至可以将所有元数据视为随机变量,例如位置、时间、光圈、焦距、ISO、对焦距离和相机类型。所有这些都是联合发生的随机变量。当我们处理多个随机变量时,会有若干个变量是我们感兴趣的:
6.2.1. 联合概率
第一个被称为 联合概率(joint probability) P ( A = a , B = b ) P(A=a,B=b) P(A=a,B=b)。给定任意值 a a a 和 b b b,联合概率可以回答: A = a A=a A=a和 B = b B=b B=b同时满足的概率是多少?请注意,对于任何 a a a 和 b b b 的取值, P ( A = a , B = b ) ≤ P ( A = a ) P(A = a, B=b) \leq P(A=a) P(A=a,B=b)≤P(A=a)。这点是确定的,因为要同时发生 A = a A=a A=a 和 B = b B=b B=b, A = a A=a A=a 就必须发生, B = b B=b B=b 也必须发生(反之亦然)。因此, A = a A=a A=a 和 B = b B=b B=b 同时发生的可能性不大于 A = a A=a A=a 或是 B = b B=b B=b 单独发生的可能性。
6.2.2. 条件概率
联合概率的不等式带给我们一个有趣的比率: 0 ≤ P ( A = a , B = b ) P ( A = a ) ≤ 1 0 \leq \frac{P(A=a, B=b)}{P(A=a)} \leq 1 0≤P(A=a)P(A=a,B=b)≤1。我们称这个比率为条件概率(conditional probability), 并用 P ( B = b ∣ A = a ) P(B=b \mid A=a) P(B=b∣A=a) 表示它:它是 B = b B=b B=b 的概率,前提是 A = a A=a A=a 已发生。
6.2.3. 贝叶斯定理
使用条件概率的定义,我们可以得出统计学中最有用的方程之一:Bayes定理(Bayes’ theorem)。根据乘法法则(multiplication rule)可得到 P ( A , B ) = P ( B ∣ A ) P ( A ) P(A, B) = P(B \mid A) P(A) P(A,B)=P(B∣A)P(A)。 根据对称性,可得到 P ( A , B ) = P ( A ∣ B ) P ( B ) P(A, B) = P(A \mid B) P(B) P(A,B)=P(A∣B)P(B)。 假设 P ( B ) > 0 P(B)>0 P(B)>0,求解其中一个条件变量,我们得到
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) . P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}. P(A∣B)=P(B)P(B∣A)P(A).请注意,这里我们使用紧凑的表示法:其中 P ( A , B ) P(A, B) P(A,B) 是一个联合分布(joint distribution), P ( A ∣ B ) P(A \mid B) P(A∣B) 是一个条件分布(conditional distribution)。这种分布可以在给定值 A = a , B = b A = a, B=b A=a,B=b 上进行求值。
6.2.4. 边际化
为了能进行事件概率求和,我们需要求和法则(sum rule),即 B B B 的概率相当于计算 A A A的所有可能选择,并将所有选择的联合概率聚合在一起:
P ( B ) = ∑ A P ( A , B ) , P(B) = \sum_{A} P(A, B), P(B)=A∑P(A,B),这也称为 边际化(marginalization)。 边际化结果的概率或分布称为 边际概率(marginal probability) 或 边际分布(marginal distribution)。
6.2.5. 独立性
另一个有用属性是 依赖(dependence) 与 独立(independence)。 如果两个随机变量 A A A 和 B B B 是独立的,意味着事件 A A A 的发生跟 B B B 事件的发生无关。在这种情况下,统计学家通常将这一点表述为 A ⊥ B A \perp B A⊥B。根据贝叶斯定理,马上就能同样得到 P ( A ∣ B ) = P ( A ) P(A \mid B) = P(A) P(A∣B)=P(A)。在所有其他情况下,我们称 A A A 和 B B B 依赖。比如,两次连续抛出一个骰子的事件是相互独立的。相比之下,灯开关的位置和房间的亮度并不是(因为可能存在灯泡坏掉、电源故障,或者开关故障)。
由于 P ( A ∣ B ) = P ( A , B ) P ( B ) = P ( A ) P(A \mid B) = \frac{P(A, B)}{P(B)} = P(A) P(A∣B)=P(B)P(A,B)=P(A) 等价于 P ( A , B ) = P ( A ) P ( B ) P(A, B) = P(A)P(B) P(A,B)=P(A)P(B),因此两个随机变量是独立的,当且仅当两个随机变量的联合分布是其各自分布的乘积。同样地,给定另一个随机变量 C C C 时,两个随机变量 A A A 和 B B B 是 条件独立的(conditionally independent),当且仅当 P ( A , B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) P(A, B \mid C) = P(A \mid C)P(B \mid C) P(A,B∣C)=P(A∣C)P(B∣C)。这个情况表示为 A ⊥ B ∣ C A \perp B \mid C A⊥B∣C。
6.2.6. 应用
我们实战演练一下!假设一个医生对患者进行艾滋病病毒(HIV)测试。这个测试是相当准确的,如果患者健康但测试显示他患病,这个概率只有1%;如果患者真正感染 HIV,它永远不会检测不出。我们使用 D 1 D_1 D1 来表示诊断结果(如果阳性,则为 1 1 1,如果阴性,则为 0 0 0), H H H 来表示感染艾滋病病毒的状态(如果阳性,则为 1 1 1,如果阴性,则为 0 0 0)。现有条件概率:
| 条件概率 | H = 1 H=1 H=1 | H = 0 H=0 H=0 |
|---|---|---|
| P ( D 1 = 1 ∣ H ) P(D_1=1|H) P(D1=1∣H) | 1 | 0.01 |
| P ( D 1 = 0 ∣ H ) P(D_1=0|H) P(D1=0∣H) | 0 | 0.99 |
Table: 条件概率为 P ( D 1 ∣ H ) P(D_1 \mid H) P(D1∣H)
请注意,每列的加和都是1(但每行的加和不是),因为条件概率需要总和为1,就像概率一样。让我们计算如果测试出来呈阳性,患者感染HIV的概率,即 P ( H = 1 ∣ D 1 = 1 ) P(H = 1 \mid D_1 = 1) P(H=1∣D1=1)。显然,这将取决于疾病有多常见,因为它会影响错误警报的数量。假设人口总体是相当健康的,例如, P ( H = 1 ) = 0.0015 P(H=1) = 0.0015 P(H=1)=0.0015。为了应用贝叶斯定理,我们需要运用边际化和乘法法则来确定:
P ( D 1 = 1 ) = P ( D 1 = 1 , H = 0 ) + P ( D 1 = 1 , H = 1 ) = P ( D 1 = 1 ∣ H = 0 ) P ( H = 0 ) + P ( D 1 = 1 ∣ H = 1 ) P ( H = 1 ) = 0.011485. \begin{split}\begin{aligned} &P(D_1 = 1) \\ =& P(D_1=1, H=0) + P(D_1=1, H=1) \\ =& P(D_1=1 \mid H=0) P(H=0) + P(D_1=1 \mid H=1) P(H=1) \\ =& 0.011485. \end{aligned}\end{split} ===P(D1=1)P(D1=1,H=0)+P(D1=1,H=1)P(D1=1∣H=0)P(H=0)+P(D1=1∣H=1)P(H=1)0.011485.
因此,我们得到
P ( H = 1 ∣ D 1 = 1 ) = P ( D 1 = 1 ∣ H = 1 ) P ( H = 1 ) P ( D 1 = 1 ) = 0.1306 . \begin{split}\begin{aligned} &P(H = 1 \mid D_1 = 1)\\ =& \frac{P(D_1=1 \mid H=1) P(H=1)}{P(D_1=1)} \\ =& 0.1306 \end{aligned}.\end{split} ==P(H=1∣D1=1)P(D1=1)P(D1=1∣H=1)P(H=1)0.1306.
换句话说,尽管使用了非常准确的测试,患者实际上患有艾滋病的几率只有 13.06%。 正如我们所看到的,概率可能是违反直觉的。
患者在收到这样可怕的消息后应该怎么办? 很可能,患者会要求医生进行另一次测试来确定病情。 第二个测试具有不同的特性,它不如第一个测试那么精确,如下所示:
| 条件概率 | H = 1 H=1 H=1 | H = 0 H=0 H=0 |
|---|---|---|
| P ( D 2 = 1 ∣ H ) P(D_2=1|H) P(D2=1∣H) | 0.98 | 0.03 |
| P ( D 2 = 0 ∣ H ) P(D_2=0|H) P(D2=0∣H) | 0.02 | 0.97 |
Table: 条件概率为 P ( D 2 ∣ H ) P(D_2 \mid H) P(D2∣H)
不幸的是,第二次测试也显示阳性。让我们通过假设条件独立性来计算出应用Bayes定理的必要概率:
P ( D 1 = 1 , D 2 = 1 ∣ H = 0 ) = P ( D 1 = 1 ∣ H = 0 ) P ( D 2 = 1 ∣ H = 0 ) = 0.0003 , \begin{split}\begin{aligned} &P(D_1 = 1, D_2 = 1 \mid H = 0) \\ =& P(D_1 = 1 \mid H = 0) P(D_2 = 1 \mid H = 0) \\ =& 0.0003, \end{aligned}\end{split} ==P(D1=1,D2=1∣H=0)P(D1=1∣H=0)P(D2=1∣H=0)0.0003,
P ( D 1 = 1 , D 2 = 1 ∣ H = 1 ) = P ( D 1 = 1 ∣ H = 1 ) P ( D 2 = 1 ∣ H = 1 ) = 0.98. \begin{split}\begin{aligned} &P(D_1 = 1, D_2 = 1 \mid H = 1) \\ =& P(D_1 = 1 \mid H = 1) P(D_2 = 1 \mid H = 1) \\ =& 0.98. \end{aligned}\end{split} ==P(D1=1,D2=1∣H=1)P(D1=1∣H=1)P(D2=1∣H=1)0.98.现在我们可以应用边际化和乘法规则:
P ( D 1 = 1 , D 2 = 1 ) = P ( D 1 = 1 , D 2 = 1 , H = 0 ) + P ( D 1 = 1 , D 2 = 1 , H = 1 ) = P ( D 1 = 1 , D 2 = 1 ∣ H = 0 ) P ( H = 0 ) + P ( D 1 = 1 , D 2 = 1 ∣ H = 1 ) P ( H = 1 ) = 0.00176955. \begin{split}\begin{aligned} &P(D_1 = 1, D_2 = 1) \\ =& P(D_1 = 1, D_2 = 1, H = 0) + P(D_1 = 1, D_2 = 1, H = 1) \\ =& P(D_1 = 1, D_2 = 1 \mid H = 0)P(H=0) + P(D_1 = 1, D_2 = 1 \mid H = 1)P(H=1)\\ =& 0.00176955. \end{aligned}\end{split} ===P(D1=1,D2=1)P(D1=1,D2=1,H=0)+P(D1=1,D2=1,H=1)P(D1=1,D2=1∣H=0)P(H=0)+P(D1=1,D2=1∣H=1)P(H=1)0.00176955.最后,鉴于存在两次阳性检测,患者患有艾滋病的概率为:
P ( H = 1 ∣ D 1 = 1 , D 2 = 1 ) = P ( D 1 = 1 , D 2 = 1 ∣ H = 1 ) P ( H = 1 ) P ( D 1 = 1 , D 2 = 1 ) = 0.8307. \begin{split}\begin{aligned} &P(H = 1 \mid D_1 = 1, D_2 = 1)\\ =& \frac{P(D_1 = 1, D_2 = 1 \mid H=1) P(H=1)}{P(D_1 = 1, D_2 = 1)} \\ =& 0.8307. \end{aligned}\end{split} ==P(H=1∣D1=1,D2=1)P(D1=1,D2=1)P(D1=1,D2=1∣H=1)P(H=1)0.8307.也就是说,第二次测试使我们能够对患病的情况获得更高的信心。尽管第二次检验比第一次检验的准确性要低得多,但它仍然显著提高我们的预测概率。
6.3. 期望和方差
为了概括概率分布的关键特征,我们需要一些测量方法。一个随机变量 X X X的期望(expectation,或平均值(average))表示为
E [ X ] = ∑ x x P ( X = x ) . E[X] = \sum_{x} x P(X = x). E[X]=x∑xP(X=x).当函数 f ( x ) f(x) f(x)的输入是从分布 P P P中抽取的随机变量时, f ( x ) f(x) f(x)的期望值为
E x ∼ P [ f ( x ) ] = ∑ x f ( x ) P ( x ) . E_{x \sim P}[f(x)] = \sum_x f(x) P(x). Ex∼P[f(x)]=x∑f(x)P(x).在许多情况下,我们希望衡量随机变量(X)与其期望值的偏置。这可以通过方差来量化:
V a r [ X ] = E [ ( X − E [ X ] ) 2 ] = E [ X 2 ] − E [ X ] 2 . \mathrm{Var}[X] = E\left[(X - E[X])^2\right] = E[X^2] - E[X]^2. Var[X]=E[(X−E[X])2]=E[X2]−E[X]2.方差的平方根被称为 标准差(standard deviation)。随机变量函数的方差衡量的是:当从该随机变量分布中采样不同值 x x x 时,函数值偏离该函数的期望的程度:
V a r [ f ( x ) ] = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ] . \mathrm{Var}[f(x)] = E\left[\left(f(x) - E[f(x)]\right)^2\right]. Var[f(x)]=E[(f(x)−E[f(x)])2].
6.4. 小结
- 我们可以从概率分布中采样;
- 我们可以使用联合分布、条件分布、Bayes定理、边缘化和独立性假设来分析多个随机变量;
- 期望和方差为概率分布的关键特征的概括提供了实用的度量形式。
7. 查阅文档
虽然文中不可能介绍每一个PyTorch函数和类(而且这些信息可能会很快过时),但 API 文档 以及额外的 教程 和示例提供了这样的文档。本节提供了一些关于如何探索PyTorch API的指导。
import torch
7.1 查找模块中的所有函数和类
为了知道模块中可以调用哪些函数和类,我们调用 dir 函数。例如,我们可以查询随机数生成模块中的所有属性:
print(dir(torch.distributions))
[‘AbsTransform’, ‘AffineTransform’, ‘Bernoulli’, ‘Beta’, ‘Binomial’, ‘CatTransform’, ‘Categorical’, ‘Cauchy’, ‘Chi2’, ‘ComposeTransform’, ‘ContinuousBernoulli’, ‘CorrCholeskyTransform’, ‘Dirichlet’, ‘Distribution’, ‘ExpTransform’, ‘Exponential’, ‘ExponentialFamily’, ‘FisherSnedecor’, ‘Gamma’, ‘Geometric’, ‘Gumbel’, ‘HalfCauchy’, ‘HalfNormal’, ‘Independent’, ‘IndependentTransform’, ‘Kumaraswamy’, ‘LKJCholesky’, ‘Laplace’, ‘LogNormal’, ‘LogisticNormal’, ‘LowRankMultivariateNormal’, ‘LowerCholeskyTransform’, ‘MixtureSameFamily’, ‘Multinomial’, ‘MultivariateNormal’, ‘NegativeBinomial’, ‘Normal’, ‘OneHotCategorical’, ‘OneHotCategoricalStraightThrough’, ‘Pareto’, ‘Poisson’, ‘PowerTransform’, ‘RelaxedBernoulli’, ‘RelaxedOneHotCategorical’, ‘ReshapeTransform’, ‘SigmoidTransform’, ‘SoftmaxTransform’, ‘StackTransform’, ‘StickBreakingTransform’, ‘StudentT’, ‘TanhTransform’, ‘Transform’, ‘TransformedDistribution’, ‘Uniform’, ‘VonMises’, ‘Weibull’, ‘Wishart’, ‘all’, ‘builtins’, ‘cached’, ‘doc’, ‘file’, ‘loader’, ‘name’, ‘package’, ‘path’, ‘spec’, ‘bernoulli’, ‘beta’, ‘biject_to’, ‘binomial’, ‘categorical’, ‘cauchy’, ‘chi2’, ‘constraint_registry’, ‘constraints’, ‘continuous_bernoulli’, ‘dirichlet’, ‘distribution’, ‘exp_family’, ‘exponential’, ‘fishersnedecor’, ‘gamma’, ‘geometric’, ‘gumbel’, ‘half_cauchy’, ‘half_normal’, ‘identity_transform’, ‘independent’, ‘kl’, ‘kl_divergence’, ‘kumaraswamy’, ‘laplace’, ‘lkj_cholesky’, ‘log_normal’, ‘logistic_normal’, ‘lowrank_multivariate_normal’, ‘mixture_same_family’, ‘multinomial’, ‘multivariate_normal’, ‘negative_binomial’, ‘normal’, ‘one_hot_categorical’, ‘pareto’, ‘poisson’, ‘register_kl’, ‘relaxed_bernoulli’, ‘relaxed_categorical’, ‘studentT’, ‘transform_to’, ‘transformed_distribution’, ‘transforms’, ‘uniform’, ‘utils’, ‘von_mises’, ‘weibull’, ‘wishart’]
通常,我们可以忽略以 __(双下划线) 开始和结束的函数(它们是Python中的特殊对象), 或以单个 _(单下划线) 开始的函数(它们通常是内部函数),可见下图所示。根据剩余的函数名或属性名,我们可能会猜测这个模块提供了各种生成随机数的方法,包括从 均匀分布(uniform)、正态分布(normal)、多项分布(multinomial)中采样。
7.2 查找特定函数和类的用法
有关如何使用给定函数或类的更具体说明,我们可以调用help函数。例如,我们来查看张量 ones 函数的用法。
help(torch.ones)
Help on built-in function ones:
ones(...)
ones(*size, *, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) -> Tensor
Returns a tensor filled with the scalar value 1, with the shape defined
by the variable argument size.
Args:
size (int...): a sequence of integers defining the shape of the output tensor.
Can be a variable number of arguments or a collection like a list or tuple.
Keyword arguments:
out (Tensor, optional): the output tensor.
dtype (torch.dtype, optional): the desired data type of returned tensor.
Default: if None, uses a global default (see torch.set_default_tensor_type()).
layout (torch.layout, optional): the desired layout of returned Tensor.
Default: torch.strided.
device (torch.device, optional): the desired device of returned tensor.
Default: if None, uses the current device for the default tensor type
(see torch.set_default_tensor_type()). device will be the CPU
for CPU tensor types and the current CUDA device for CUDA tensor types.
requires_grad (bool, optional): If autograd should record operations on the
returned tensor. Default: False.
Example::
>>> torch.ones(2, 3)
tensor([[ 1., 1., 1.],
[ 1., 1., 1.]])
>>> torch.ones(5)
tensor([ 1., 1., 1., 1., 1.])
从文档中,我们可以看到 ones 函数创建一个具有指定形状的新张量,并将所有元素值设置为 1 1 1。让我们来运行一个快速测试来确认这一解释:
torch.ones(4)
tensor([1., 1., 1., 1.])
在 Jupyter 记事本中,我们可以使用 ? 指令在另一个浏览器窗口中显示文档:
- list?指令将创建与help(list)指令几乎相同的内容,并在新的浏览器窗口中显示它
- 如果我们使用两个问号,如 list??,将显示实现该函数的 Python 代码
7.3 小结
- 官方文档提供了本书之外的大量描述和示例。
- 我们可以通过调用
dir和help函数 或 在Jupyter记事本中使用?和??查看API的用法文档。
更多推荐
 已为社区贡献21条内容
已为社区贡献21条内容








所有评论(0)