论文信息

地址：https://rpg.ifi.uzh.ch/docs/omnidirectional_camera.pdf
作者Davide Scaramuzza
单位：GRASP Lab, University of Pennsylvania

定义

(全方位摄像机)An omnidirectional camera (from omni, meaning all) is a camera with a 360-degree field of view in the horizontal plane, or with a visual field that covers a hemisphere or (approximately) the entire sphere.

Background

大多数相机是可以用小孔成像pinhole cameras，但是Omni 全向相机不行。一般采用一下几种方法

当然，我会用简单的话来解释这三种全向相机（omnidirectional camera）的构建方式。

1. 折射相机（Dioptric cameras）：

   • 这种相机使用了不同形状的镜头，例如鱼眼镜头。
   • 它的视野可以超过180度，也就是稍微超过半个球。
   • 你可以想象它的镜头像一个鱼眼，能够捕捉到更广泛的视野。

2. 折反射相机（Catadioptric cameras）：

   • 这种相机结合了普通的相机和一个特殊形状的镜子，比如抛物面镜、双曲面镜或椭圆面镜。
   • 它可以在水平方向上提供360度的视野，在垂直方向上也有超过100度的视野。
   • 你可以想象它像一个带有曲面镜的全方位摄像头，可以捕捉到周围的所有东西。
   • 图1b中展示了一个使用双曲面镜的折反射相机的例子。

3. 多折射相机（Polydioptric cameras）：

   • 这种相机使用了多个摄像头，并且每个摄像头的视野都是重叠的。
   • 目前，这种相机是唯一能够提供真正的全向（球形）视野的相机，也就是说，它可以捕捉到所有方向（360度×360度）的图像。
   • 你可以想象它像是一个由多个摄像头组成的球体，每个摄像头都能捕捉到一部分图像，而所有这些图像组合起来就能形成一个完整的球形视野。

希望这些解释能够帮助你更好地理解这三种全向相机的构建方式！

直到2000年，由于新的制造技术和精密工具，鱼眼相机才开始普及，使其视野增加到180度甚至更多。然而，直到2005年，这些相机才被小型化到1-2厘米的大小，并且它们的视野增加到190度甚至更大）。

鱼眼是全向相机的折射相机的一种重要类型。

0.1 中央全向相机

0.1.1 中央相机 projection center or single effective viewpoint

中心投影系统：当被观察物体的光线在3D空间中的一个点（即投影中心或单有效视点）相交时，视觉系统被称为中心投影系统。在这个系统中，所有的光线都通过一个单一的点（如相机的镜头中心）投射到图像平面上。这个属性被称为单一有效视点属性。
（图2）

形成单一有效视点包括：透视相机、鱼眼相机和特色设计的折反射相机。

透视相机（perspective camera）是中央投影系统的一个示例，因为所有光线（optical rays）在一个点（即相机光学中心）相交。

鱼眼相机是一种能够捕获广角甚至全向视图的特殊镜头。虽然其镜头设计特殊，但它们的成像原理仍基于中心投影系统，因此满足单一有效视点的特性。

相反，中央折反射相机为了实现单一有效视点的特性，需要仔细选择镜子的形状和相机与镜子之间的距离。Baker和Nayar的研究表明，满足这一特性的镜子形状是双曲线、抛物线和椭圆形的旋转体。

对于双曲线镜和椭圆镜，通过确保相机中心（即针孔或透镜中心）与双曲线（椭圆）的一个焦点重合来实现单视点特性（图3）。对于抛物面反射镜，必须在相机和反射镜之间插入正交透镜，这使得抛物面反射镜反射的平行光线可能会聚到相机中心（图3）。

单一有效视点的优势：

• 几何正确的透视图像：由于每个像素都对应于通过视点的特定方向的光线，因此可以从全向相机拍摄的图片中生成几何正确的透视图像。单一有效视点之所以如此理想，是因为它允许用户从全向相机拍摄的图片中生成几何正确的透视图像（图4）。

• 应用视极几何理论：单视点属性允许用户应用视极几何理论，这对于从运动恢复结构（structure from motion）等计算机视觉任务非常重要。

单视点属性如此重要的另一个原因是它允许用户应用著名的视极几何理论，这对从运动到结构非常重要。极向几何适用于任何中央相机，无论是透视还是全向。

中央相机（Central cameras）如何将全向图像（omnidirectional image）的特定区域重新映射（remap）到透视图像（perspective image）上，或者投影到一个球体上。以下是对这段话的理解：

1. 重新映射到透视图像：

   • 中央相机允许用户通过指定一个由用户任意定义的平面（a），来将全向图像中的某个区域重新映射到一个透视图像上。
   • 在这个过程中，光线（optical rays）与这个平面相交，形成透视图像。

2. 不能将整个全向图像投影到平面上：

   • 由于全向图像捕捉了几乎360度的视野，因此不可能将整个全向图像直接投影到一个平面上而不发生变形或损失。
   • 只能将全向图像的某些子区域（subregions）投影到平面上，以生成透视图像。

3. 投影到球体上：

   • 另一种选择是将全向图像投影到一个球体上（c）。
   • 在这种情况下，整个全向图像可以被完整地重新映射到球体上，而不会发生变形或损失。

这样的重新映射或投影技术对于许多应用来说非常重要，如虚拟现实、增强现实、视频监控和机器人导航等。它们允许用户或系统从全向相机捕捉的全景数据中提取特定区域的详细信息，或将其转化为更适合进一步处理或显示的形式。

0.1.2 鱼眼相机不是透视相机，但属于折射相机

鱼眼相机不是传统意义上的透视相机。虽然鱼眼相机和透视相机都用于捕捉图像，但它们在成像原理和图像特性上有显著的差异。

1. 成像原理：透视相机遵循中心投影系统的原理，即所有光线通过一个单一的点（镜头中心）投射到图像平面上，形成透视图像。而鱼眼相机则使用一种特殊设计的镜头，该镜头具有极大的视角（通常超过180度），可以捕捉几乎全方位的图像。鱼眼相机的镜头使入射光线的入射角远远大于普通镜头，并且使得光线在图像平面上呈现出一种特殊的弯曲或变形，这被称为“鱼眼效应”。

2. 图像特性：透视相机捕捉的图像具有线性的透视关系，即远处的物体在图像中看起来较小，近处的物体看起来较大。而鱼眼相机捕捉的图像则具有非线性的透视关系，图像中的物体可能会出现明显的畸变和变形，尤其是边缘部分的物体。

3. 应用场景：透视相机广泛应用于各种摄影和视觉系统中，因为它们能够生成符合人眼感知的透视图像。而鱼眼相机则更适用于需要捕捉全方位图像的场景，如监控、虚拟现实、自动驾驶等领域。

因此，虽然鱼眼相机和透视相机都是用于捕捉图像的相机，但它们在成像原理和图像特性上存在显著的差异，不能简单地将鱼眼相机归类为透视相机。

0.2 全向相机模型和标定

在之前的博客【鱼眼镜头1】鱼眼镜头的四种投影模型（指导镜头的设计），中央镜头综述，说明了投影模型的重要性：为了从全向相机捕获的图像中提取有用的信息，我们需要知道光线如何从三维空间映射到二维图像平面。这就是投影模型的作用。一个准确的投影模型可以帮助我们更准确地估计场景中物体的位置、姿态和其他属性。

常见的鱼眼相机基本成像模型主要有四种，它们分别是等距投影（最广泛）、等立体角投影、体视投影、正交投影。镜头的设计基本是按照上述四种投影模型而制作的，可看出鱼眼相机成像模型通用性较差。

为了解决模型通用性较差的问题，可以引入畸变模型，将鱼眼成像模型等价成理想针孔成像模型与畸变模型的叠加作用。

以上是之前对鱼眼相机的标定和投影模型的理解。鱼眼相机由于其超大的视场角（Field of View, FOV），其成像过程并不完全符合传统的针孔相机模型。因此，需要使用特定的投影模型来描述鱼眼相机的成像过程。

1. Equidistant模型：

   • Equidistant模型（等距投影模型）是一种常用的鱼眼相机投影模型。在这个模型中，图像半径rd与入射角Θ（光线与相机光轴的夹角）之间的关系是线性的，即rd = f * Θ，其中f是相机的焦距。这个模型假设在图像平面上，沿各个方向上的距离都是等比例缩放的。

2. 鱼眼相机的实际设计：

   • 对于实际的鱼眼镜头来说，由于制造和设计的限制，它们不可能完全精确地按照某个特定的投影模型来设计。因此，为了更准确地描述鱼眼相机的成像过程，需要使用更复杂的模型或近似方法。

3. Kannala的鱼眼相机多项式近似模型：

   • Kannala提出了一种鱼眼相机的一般多项式近似模型。这个模型使用多项式来近似描述图像半径rd与入射角Θ之间的关系。这种方法的优点是可以更灵活地适应不同鱼眼相机的成像特性，提高标定的准确性。

4. 奇函数和泰勒级数展开：
   

   • 在讨论鱼眼相机的投影模型时，提到了${\Theta }_d$是$\Theta$的奇函数。这意味着当$\Theta$取正值和负值时，${\Theta }_d$的绝对值相同但符号相反。这是因为鱼眼相机的成像过程在光轴的两侧是对称的。
   • 将投影模型按泰勒级数展开，可以发现${\Theta }_d$可以用$\Theta$的奇次多项式来表示。这是因为奇次多项式在原点附近是对称的，这与鱼眼相机的成像特性相符。

综上所述，使用Equidistant模型可以简化鱼眼相机的成像过程，但实际的鱼眼镜头可能无法完全遵循这个模型。为了更准确地描述鱼眼相机的成像过程，可以使用更复杂的模型或近似方法，如Kannala的多项式近似模型。同时，通过泰勒级数展开和奇函数性质的分析，可以更好地理解这些投影模型的特点和适用性。

opencv中的fisheye::calibrate就是用的该畸变模型. 也叫作kannala-brandt模型.

全向相机的模型比标准的透视相机模型要复杂

直观上，全向相机的模型比标准的透视相机模型要复杂一些。全向相机模型需要考虑一些额外的因素，例如在使用折反射相机（catadioptric camera）时，需要考虑镜面的反射作用；而在使用鱼眼相机（fisheye camera）时，则需要考虑镜头引起的折射效应。由于这个领域的文献相当丰富，本章将回顾两种已成为全向视觉和机器人学中标准的投影模型。此外，针对这两种模型，已经开发了Matlab工具箱，这些工具箱在全球范围内被专家和非专家广泛使用。

第一种 统一投影模型（在鱼眼应用受限）

Geyer 和 Daniilidis 在 2000 年发表的具有里程碑意义的论文。

关于统一投影模型（Unified Projection Model）的解释如下：

1. 模型概述：

   • 统一投影模型（Unified Projection Model）是为中央折反射相机（central catadioptric cameras）设计的。
   • 该模型由Geyer和Daniilidis在2000年提出，后来被Barreto和Araujo进一步改进。
   • 它的特点是能够涵盖使用双曲面、抛物面或椭圆面镜子的所有三种类型的中央折反射相机。

2. 模型特点：

   • 通用性：统一投影模型不仅适用于单一类型的中央折反射相机，还能适应不同镜面形状（双曲面、抛物面、椭圆面）的相机。
   • 精确性：该模型被设计用于精确地描述光线如何通过中央折反射相机的镜面反射并最终投影到图像平面上。
   • 针对性：虽然统一投影模型可以近似地用于鱼眼相机，但它在设计上是专门针对中央折反射相机的，对于鱼眼相机的描述可能只有有限的准确性。

3. 模型应用：

   • 由于其通用性和精确性，统一投影模型在全向视觉和机器人学等领域得到了广泛应用。
   • 特别是在需要准确捕捉和解析大视场角图像的场景中，如全景监控、虚拟现实、机器人导航等。

4. 与鱼眼相机的关系：

   • 尽管统一投影模型最初是为中央折反射相机设计的，但研究人员已经尝试将其用于近似描述鱼眼相机的成像过程。
   • 然而，由于鱼眼相机的成像原理与折反射相机存在本质差异（如折射效应），因此这种近似通常只具有有限的准确性。

综上所述，统一投影模型是一个为中央折反射相机设计的精确且通用的投影模型，它在大视场角图像的捕获和处理中发挥着重要作用。尽管可以尝试将其用于近似描述鱼眼相机的成像过程，但由于两种相机成像原理的差异，这种近似的准确性有限。

第二个 Taylor模型（适用于鱼眼相机）

第二个模型在一个通用模型下统一了中央折反射相机和鱼眼相机，这个模型也被称为Taylor模型。以下是关于这个模型的详细解释：

1. 模型背景：

   • Taylor模型由Scaramuzza等人于2006年开发，旨在统一描述中央折反射相机和鱼眼相机的投影过程。

2. 模型特点：

   • 通用性：Taylor模型不仅适用于中央折反射相机，也适用于鱼眼相机，通过相同的数学模型（Taylor多项式）来描述这两种不同类型的相机。
   • 精确性：Taylor多项式可以根据不同相机的特性进行调整，以更准确地描述光线如何从三维空间映射到二维图像平面。

3. 模型优势：

   • 相比之前只能描述单一类型相机的模型，Taylor模型为研究人员提供了一个统一的框架，可以方便地应用于全向视觉和机器人学中的不同场景。
   • 由于其通用性和灵活性，Taylor模型在相机标定、图像校正以及后续的视觉处理任务中都表现出色。

4. 模型应用：

   • 在全向视觉系统中，Taylor模型可以用于相机的精确标定，从而确保捕获的图像具有正确的几何关系。
   • 在机器人导航和自主驾驶等领域，Taylor模型可以帮助机器人准确感知周围环境，实现安全的导航和避障。

5. 与统一投影模型的区别：

   • 统一投影模型是专门为中央折反射相机设计的，而Taylor模型则同时适用于中央折反射相机和鱼眼相机。
   • 在描述相机投影过程时，Taylor模型采用了更灵活的Taylor多项式形式，可以更好地适应不同相机的特性。

综上所述，Taylor模型是一个能够统一描述中央折反射相机和鱼眼相机的通用投影模型。它通过Taylor多项式来模拟光线从三维空间到二维图像平面的映射过程，具有通用性、灵活性和精确性等优点。

0.3 Unified model for central catadioptric cameras

只有推导了这个才能推导Taylor模型。

在【鱼眼镜头5】[中央全向相机畸变模型]：统一相机模型，四阶多项式对统一相机模型进行建模 解释了统一模型。

Geyer & Daniilidis(2000)为所有中央折射系统提供了统一的理论，在文献中被称为统一投影模型，广泛应用于不同的校准工具箱(Mei & Rives (2007);Heng等(2013,2015))。他们证明了每一个投影，无论是标准视角还是利用双曲反射镜、抛物面镜或椭圆镜，可以用投影映射从球面到投影中心位于球面直径和垂直于球面的平面进行建模。

Unified Model: 我们使用的模型的核心思想是连接两个连续的投影，第一个投影将点从世界坐标系下投影到以相机为中心的单位球体上。接着是一个将光心沿着光轴移动-δ普通的针孔相机投影。模型使用5个参数来描述，fx, fy, cx, cy, δ。

这个模型的优势是方便于计算投影与反投影的函数，注意当δ为0的时候退化为一个简单的针孔模型。同样的，我们可以在这个模型上添加上小的径向-切向畸变，可以对图像进行去畸变后更好的适应这个模型。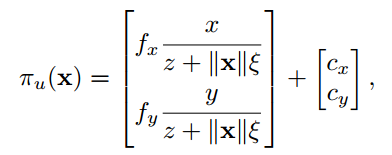

我在【鱼眼镜头5】[中央全向相机畸变模型]：统一相机模型，四阶多项式对统一相机模型进行建模 说“四阶多项式建模”Scaramuzza和Martinelli(2006)提出用泰勒级数展开对成像函数进行建模，泰勒级数展开的程和系数是待估计的参数。三阶或四阶多项式能够准确地建模所有的反射摄像机和多种鱼眼摄像机。Mei & Rives(2007)在统一项目基础上进行改进，通过对具有良好识别参数的失真模型进行建模来考虑现实世界中的错误。

推导过程

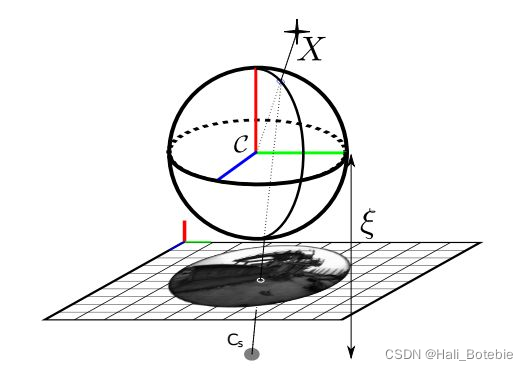
这节内容的目的是找出从场景点到其对应图像点的像素坐标的观看方向之间的关系。Geyer 和 Daniilidis 的投影模型遵循一个四步过程。以下是对这段内容的逐步解释：

1. 场景点投影到单位球上：

   • 假设 P = (x, y, z) 是以 C 为中心的镜像参考系中的一个场景点。
   • 将 P 投影到单位球上得到 Ps = P / ||P|| = (xs, ys, zs)。这一步是将场景点标准化到单位球上，使得所有的点都在单位球面上。

2. 坐标变换到新参考系：

   • 新参考系的中心是 Cǫ = (0, 0, −ǫ)，其中 ǫ 的取值范围在 0（平面镜）和 1（抛物面镜）之间。
   • 将 Ps 的坐标变换到新参考系，得到 Pǫ = (xs, ys, zs + ǫ)。这一步是考虑镜面的几何特性，特别是其焦距与焦距线（latus rectum）之间的关系，从而确定 ǫ 的值。

3. 投影到归一化图像平面：

   • 将 Pǫ 投影到距离 Cǫ 为 1 的归一化图像平面上，得到 ˜m = (xm, ym, 1)。这一步是将三维坐标转换到二维图像平面上，其中 xm 和 ym 是二维图像坐标，而 1 是表示点在平面上的齐次坐标。

4. 映射到相机图像点：

   • 通过相机的内参矩阵 K 将 ˜m 映射到相机图像点 ˜p = (u, v, 1)。这一步是考虑了相机的镜头畸变、焦距和图像中心位置等内部参数，从而得到最终的像素坐标 (u, v)。

知乎朋友的智慧

5. 关于函数 g 和 g-1 的解释：

• g-1 是从单位球面上的点 Ps 到归一化图像平面上的点 ˜m 的映射函数。
• g 是 g-1 的逆函数，即从归一化图像平面上的点 ˜m 映射回单位球面上的点 Ps。
• 方程 (6) 展示了如何通过 ˜m 和 ǫ 来计算 Ps。由于 Ps 必须位于单位球面上，因此可以通过解方程 $x_s^2+y_s^2+z_s^2=1$ 来得到 zs 的表达式。

整体而言，这个投影模型是一个从三维场景点到二维图像点（通过像素坐标表示）的映射过程，它考虑了镜面的几何特性、相机的内部参数以及从三维到二维的投影关系。这个模型为理解如何通过相机捕获三维世界中的信息提供了理论基础。

该模型的意义

该模型已被证明能够准确描述所有中央折反射相机（抛物面镜、双曲面镜和椭圆镜）和标准透视相机。 Ying 和 Hu [9] 于 2004 年提出了鱼眼镜头模型的扩展。 然而，通过折反射相机来近似鱼眼相机的精度有限。 这主要是因为，虽然三种类型的中央折反射相机可以通过精确的参数函数（抛物线、双曲线、椭圆）来表示，但鱼眼镜头的投影模型因相机而异，并且取决于镜头视场。

0.4 Unified model for catadioptric and fisheye cameras

在【鱼眼镜头6】[鱼眼畸变模型]：统一相机模型标定scaramuzza多项式模型 中我介绍了Scaramuzza 多项式模型。

这个统一模型由 Scaramuzza 等人于 2006 年提出[10,11]。 与之前模型的主要区别在于函数g的选择。 为了克服对鱼眼相机参数模型知识的缺乏，作者提出使用泰勒多项式，其系数和次数是通过校准过程找到的。 相应地，归一化图像点~m = (xm, ym, 1)与鱼眼（镜面）参考系中单位向量Ps之间的关系可写为：

1. ρ 的定义：

   • $\rho =\surd (x_m^2+y_m^2)$定义了从相机光心到图像平面上某点的径向距离（在归一化图像平面上）。这里的 xm 和 ym 是归一化图像平面上的坐标，ρ 是一个标量，代表了该点与图像中心的距离。

2. 多项式模型中的一阶项缺失：

   • 文中提到，多项式模型中没有一阶项（即 a1ρ），这是因为当 ρ = 0 时（也就是图像中心），多项式的一阶导数必须为零。这一要求对于折反射相机和鱼眼相机都是成立的。对于折反射相机，这一点可以通过对方程（6）求导并验证 ρ = 0 时的导数值为零来直观验证。

3. 多项式的普适性：

   • 由于该模型采用了多项式形式，它不仅可以模拟折反射相机，还可以模拟鱼眼相机和透视相机。这种普适性是通过选择适当的多项式阶数来实现的。

4. 多项式阶数的选择：

   • 作者指出，三阶或四阶多项式能够非常准确地模拟所有折反射相机以及市场上许多类型的鱼眼相机。这种模型之所以成功，是因为它能够广泛应用于各种商业相机。

总结：

• 文中描述了一个基于多项式形式的相机模型，该模型能够灵活地模拟不同类型的相机，包括折反射相机、鱼眼相机和透视相机。通过选择适当的多项式阶数，该模型可以精确地拟合不同类型相机的投影特性。特别是，该模型在 ρ = 0 处的导数为零，这是为了满足折反射相机和鱼眼相机的投影特性。

0.5 Omnidirectional camera calibration

全向相机（如鱼眼相机和折反射相机）的标定与标准透视相机的标定相似，都涉及到通过拍摄在不同位置和姿态下的标定物图像来确定相机的内参和畸变参数。然而，对于全向相机来说，确保标定图像从相机的各个角度拍摄非常重要，而不仅仅是单一的一侧。这是为了补偿相机和镜面之间可能存在的错位。

当前，对于Matlab环境，有三种开源的标定工具箱可供选择，它们的主要区别在于所采用的投影模型和标定图案的类型。

1. MEI的工具箱：该工具箱使用棋盘格（checkerboard-like）图像，并利用Geyer和Daniilidis之前讨论的投影模型。它特别适用于使用双曲面、抛物面、折叠镜面和球面镜的折反射相机。Mei的工具箱可以从[13]下载，理论细节可以在[14]中找到。

2. Barreto的工具箱：与MEI的工具箱不同，它使用线图像而不是棋盘格。同样，它也采用Geyer和Daniilidis的投影模型。该工具箱特别适合抛物面镜。可以从[12]下载该工具箱，而理论细节可以在[15]和[16]中找到。

3. Scaramuzza的工具箱：此工具箱也使用棋盘格图像，但与前两个工具箱不同，它利用了Scaramuzza开发的针对折反射和鱼眼相机的统一泰勒（Taylor）模型。它适用于使用双曲面、抛物面、折叠镜面、球面和椭球面镜的折反射相机，以及市场上可用的多种鱼眼镜头（如Nikon、Sigma、Omnitech-Robotics等），其视野可达195度。可以从[17]下载该工具箱，而理论细节可以在[10]和[11]中找到。与前两个工具箱不同，此工具箱具有自动标定过程，即畸变中心和标定点都是自动检测的，无需用户干预。因此，这个工具箱变得非常流行，目前被NASA、Philips、Bosch、Daimler和XSens等多家公司使用。

（正文完）