智能优化算法：混沌博弈优化算法

摘要：混沌博弈优化算法（Chaos Game Optimization (CGO)）是于2020年提出的一种基于混沌理论原理的优化算法。

1.算法原理

1.1 初始化

该算法的初始化，与其他智能优化算法的初始化一样，在搜索空间范围内进行随机初始化。
$$x_i^j(0)=x_{i,min}^j+rand.(x_{i,max}^j-x_{i,min}^j)，i=1,2,...,n,j=1,2,...,d\text{\hspace{1em}(1)}$$
其中$n$为候选点的数量，$d$​为候选点的维度。$x_i^j(0)$为合格的初始位置，$x_{i,min}^j,x_{i,max}^j$为上下限。

1.2 第一种子位置更新

第一种子位置更新数学描述如下：
$$See{d}_i^1=X_i+{\alpha }_i\ast ({\beta }_i\ast GB-{\gamma }_i\ast M{G}_i)\text{\hspace{1em}(2)}$$
其中$X_i$为第$i$个候选解。$GB$为当前最优解。$M{G}_i$为初始合格点的平均值，这些点被认为是第一个临时三角形的三个顶点。${\alpha }_i$为是随机生成的矩阵，用于模拟种子的运动位置限制，而${\beta }_i$和${\gamma }_i$每个和表示0或1的随机整数。

1.3 第二种子位置更新

第二种子位置更新数学描述如下：
$$See{d}_i^2=GB+{\alpha }_i\ast ({\beta }_i\ast X_i-\gamma \ast M{G}_i)\text{\hspace{1em}(3)}$$
其中$X_i$为第$i$个候选解。$GB$为当前最优解。$M{G}_i$为初始合格点的平均值，这些点被认为是第一个临时三角形的三个顶点。${\alpha }_i$为是随机生成的矩阵，用于模拟种子的运动位置限制，而${\beta }_i$和${\gamma }_i$每个和表示0或1的随机整数。

1.4 第三种子位置更新

第三种子位置更新数学描述如下：
$$See{d}_i^3=M{G}_i+{\alpha }_i\ast ({\beta }_i\ast X_i-{\gamma }_i\ast GB)\text{\hspace{1em}(4)}$$
其中$X_i$为第$i$个候选解。$GB$为当前最优解。$M{G}_i$为初始合格点的平均值，这些点被认为是第一个临时三角形的三个顶点。${\alpha }_i$为是随机生成的矩阵，用于模拟种子的运动位置限制，而${\beta }_i$和${\gamma }_i$每个和表示0或1的随机整数。

1.5 第四种子位置更新

第四种子位置更新数学描述如下：
$$See{d}_i^4=X_i(x_i^k=x_i^k+R),k=[1,2,..,d]\text{\hspace{1em}(5)}$$
其中$k$为$[1,d]$内的随机整数向量。$R$为$[0,1]$内均匀分布随机数。为了控制和调整所提出的新的$CGO$算法的探索和开发速度，${\alpha }_i$可根据公式（6）确定。
$${\alpha }_i=\{\begin{array}{l}Rand\\ 2\ast Rand\\ \delta \ast Rand+1\\ \xi \ast Rand+(-\xi )\end{array}\text{\hspace{1em}(6)}$$
其中$Rand$为[0,1]内的随机向量。$\delta$和$\xi$为[0,1]内的随机向量。

算法流程：

步骤1：利用随机选择方法定义了搜索空间中候选解X或初始合格点的初始位置。

步骤2：根据初始合格点的自相似性计算初始候选解的适应度值。

步骤3：确定全局最佳合格点及全局最优值$GB$。

步骤4：对于搜索空间中的每个合格点$X_i$，由随机选择过程确定的平均值$M{G}_i$。

步骤5：对于搜索空间中的每个合格点$X_i$，用三个顶点$X_i,M{G}_i,G{B}_i$确定一个临时三角形。

步骤6：对于每个临时三角形，四个种子位置更新。

步骤7：重新评估种子位置并更新适应度值。

步骤8：判断是否满足最大迭代次数，若满足，则输出最优位置和全局最优解，否则，返回步骤3重新迭代计算

2.算法结果

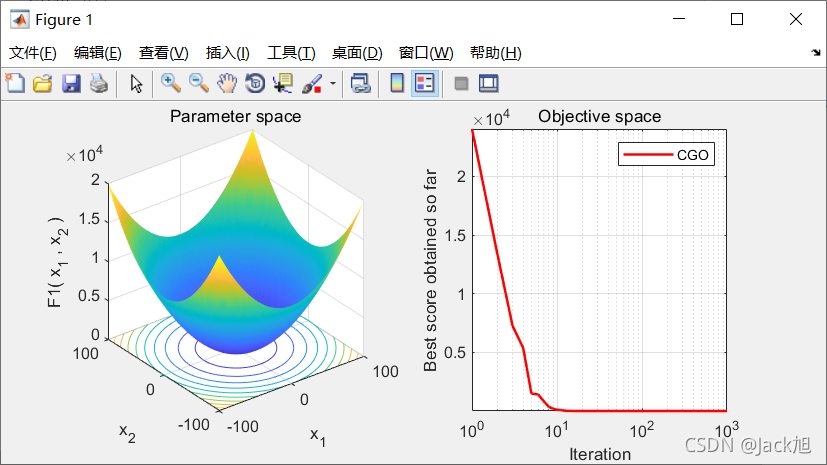
3.参考文献

[1]Talatahari, S., Azizi, M., Optimization of Constrained Mathematical and Engineering Design Problems Using Chaos Game Optimization, Computers & Industrial Engineering (2020).

4.Matlab代码