TVP-VAR-BK 溢出指数是一种用于分析金融市场或经济变量之间信息溢出效应的方法，可以帮助我们更好地理解经济系统的复杂性和动态性，以下是对其的简介：

1. TVP-VAR 模型

   • 原理：传统的向量自回归（VAR）模型假设模型的参数是固定不变的，但在实际经济环境中，经济结构、政策以及市场参与者的行为等因素都可能随时间不断变化。时变参数向量自回归（TVP-VAR）模型则放松了这一假设，允许模型的参数随时间变化，从而能够更灵活地捕捉经济系统中变量之间动态的、时变的关系。

   • 构建方式：首先确定模型的变量和滞后阶数，然后通过估计方法得到每个时点上的参数值。常用的估计方法有贝叶斯估计等，在估计过程中不断更新参数的后验分布，以反映参数的时变性。

2. TVP-VAR-BK 溢出指数的含义：

   • 信息传递方面：该指数衡量了不同金融市场或经济变量之间信息传递的程度。如果一个市场的变化会引起另一个市场的显著反应，那么就存在信息从一个市场向另一个市场的溢出。通过 TVP-VAR-BK 溢出指数可以定量地分析这种信息溢出的大小和方向，帮助研究者了解不同市场之间的关联程度和信息传递机制。

   • 时变特征方面：由于结合了 TVP-VAR 模型，所以该溢出指数能够捕捉到信息溢出效应随时间的变化。这意味着在不同的经济时期或市场环境下，金融市场或经济变量之间的信息溢出效应可能会有所不同，TVP-VAR-BK 溢出指数可以反映出这种动态变化，为政策制定者和投资者提供更准确的参考。

TVP-VAR-BK 溢出指数的优点：

1. 时变性捕捉能力：

   • 动态反映关系变化：传统的溢出指数模型通常假设参数是固定的，无法很好地捕捉经济和金融系统中变量之间关系的动态变化。而 TVP-VAR-BK 溢出指数基于时变参数向量自回归模型，能够适应经济环境、市场结构、政策变化等因素的不断演变，实时反映不同变量之间信息溢出效应的动态变化过程。例如，在不同的经济周期、金融市场波动阶段或者重大政策事件发生时，可以准确地捕捉到金融市场之间或经济变量之间信息传递和相互影响的强度、方向的变化。

   • 提供及时准确信息：这对于政策制定者和投资者来说具有重要的参考价值。政策制定者可以根据不同时期的信息溢出情况，及时调整政策以维护金融市场的稳定和经济的健康发展；投资者可以根据动态的溢出效应调整投资组合，降低风险并获取更好的投资回报。

2. 信息全面性和准确性：

   • 全面考量多变量关系：该方法可以同时考虑多个变量之间的相互关系，能够更全面地分析复杂经济系统中各个部分之间的信息传递和影响。相比于只关注两两变量之间关系的方法，TVP-VAR-BK 溢出指数可以揭示整个系统的信息溢出网络结构，帮助研究者更好地理解经济系统的整体性和复杂性。

   • 方差分解基础更可靠：BK 溢出指数是在 VAR 模型的方差分解基础上发展而来的，方差分解可以将系统中一个变量的预测误差方差分解为系统中其他变量的冲击所贡献的部分，这种方法为分析变量之间的相互影响提供了一个较为严谨的理论框架，使得 TVP-VAR-BK 溢出指数的计算结果具有较高的可靠性和解释力。

3. 灵活性和适应性：

   • 适用于多种数据类型：对于不同类型的数据，如时间序列数据、面板数据等，TVP-VAR-BK 溢出指数都可以进行有效的分析。并且对于数据的分布形态、平稳性等要求相对较低，在实际应用中具有较强的灵活性和适应性。

   • 可与其他方法结合：该方法可以与其他经济计量方法或模型相结合，进一步拓展其应用范围和分析能力。例如，可以与贝叶斯估计、机器学习等方法结合，提高模型的估计精度和预测能力。

部分代码截图如下

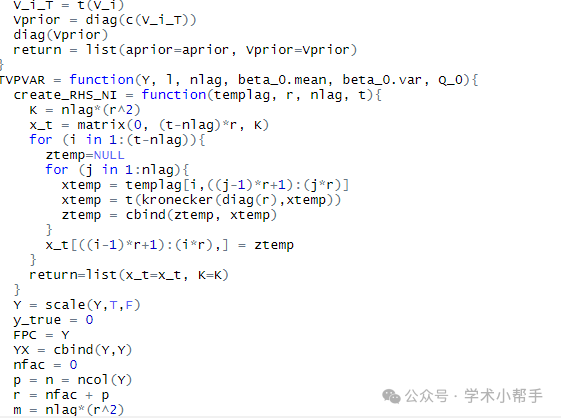
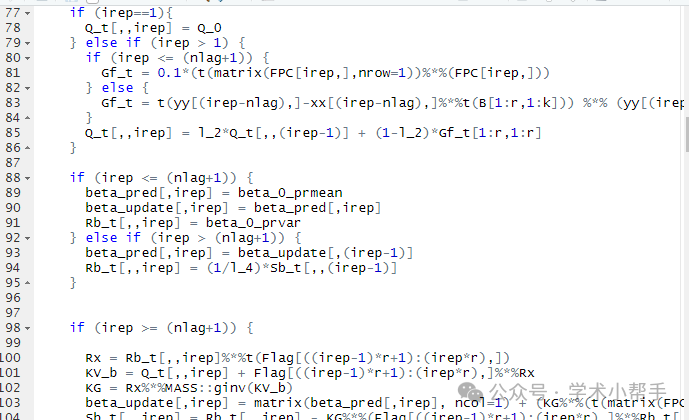
（文件包括代码、数据集及注释）

想省心省事的请直接私

其他溢出指数代码还未介绍的也可咨询：包括QVAR溢出指数、QVAR-BK溢出指数、QFVAR-DY（最新代码）、TVP-VAR-SV