蓝桥杯 试题 算法训练 礼物 (思路及代码)
蓝桥杯 算法训练 礼物O(n)解法图示讲解 思路清晰

前言
关于这道题,网上有很多解法。我搜了几篇,初看之下没看懂(我是废物),不过因为我看了题目之后也有一点思路,所以也并没有去好好理解网上其他的解法,仅是了解一下其他大佬的思路,只是没想到竟然看都看不懂。
正文
我有一点拙见。
暴力求解的话,即进行双重循环,维护一个K的最大值。当然,O(n2)级的算法显然是不能ac本题的。数据量非常大。
我一开始的思路是这样的:(后来发现这个思路细节是有误的,先按下暂且不表,待会再说)
首先明确五个变量名:在整个石头数组中,jiaoshou最终选取的——石子最多的那个数组,不妨将之分为左右两个部分,左半部分的起始位置称为left,左半部分的总重量为leftWeight,右半部分的起始位置称为right,右半部分的总重量为rightWeight,num为左(右)数组的长度,即左半(右半)部分有几颗石头。最终要输出的答案其实就是2*num。
我起变量名还是挺清晰的哈哈哈!
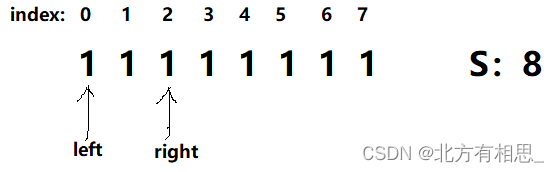
1.首先从左到右遍历整个石头数组,先找到满足num=1,且leftWeight<=S,rightWeight<=S
如下图:

2.接下来,进行一个判断,当num增加1的时候,即左右数组各自多增加一个石头的时候,能否满足左右部分各自的重量小于S。
如果能够满足,则:num=num+1;再让right往右移一格。并且更新左右部分的重量。
如果不能满足,则:num不变,让left和right同时往右移一格,并且更新左右部分的重量
如下图:
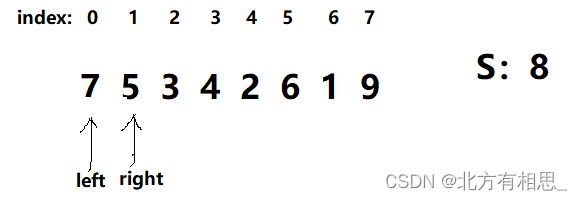
当状态为这个样子的时候,如果num=num+1,那么左半部分就有 7 5两颗石头,右半部分为 3 4两颗石头,明显不满足题意。所以状态变换至如下图:

3.然后循环继续进行第2步的操作。我就拿着上面这张图继续操作了哈。
在如上这个状态下,如果num=num+1,那么左半部分为5 3,右半部分为 4 2,符合题意。
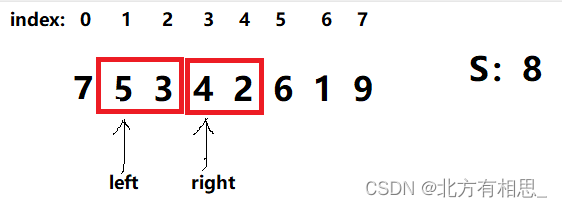
当如这样一直遍历整个石头数组,那么最终的2*num就是需要的答案!
......吗?
反思
实际上,这个思路乍一看没有毛病,实际上,却大有问题。
但是如果按照以上思路去做,竟然能过90%的样例点(哈哈哈,不得不说蓝桥杯的测评数据真的是歌姬吧)。
那么上面这个思路的错误之处在哪呢?下面我会细细讲解,并且列出正确的思路。
首先先要知道,我为什么会用这样的思路来解题:
比如,当left=1,num=2,right=3时,会处于这样一个状态。
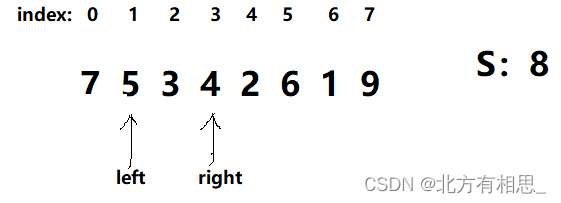
很明显,num不能继续递增了,那么我们将left和right右移。
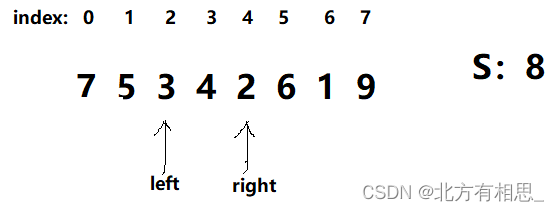
也就是说,我们没必要考虑当left=2时,num从1开始递增,而是接着之前已经得到的num进行考察。因为我们最后的答案是“最多”能一次拿走几个石头,既然我在left=1时知道了一次能拿走2个石头,那么在left=2,3,4,.......我们就没必要去看num能不能为1,而是从2接着考察(当然从3接着考察也行)。但是但是但是!我却陷入了一个误区,num=2时不满足左半和右半的重量都小于S,那num=3时也一定不满足吗?
看如下这个例子:
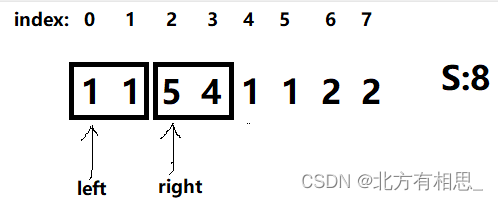
此时,num=2右半部分是不满足题意的。如果按照上面的思路,我们这时候应该将left和right 右移。
但是,在此时的left=0的条件下,如果num=3,那却是符合题意的。
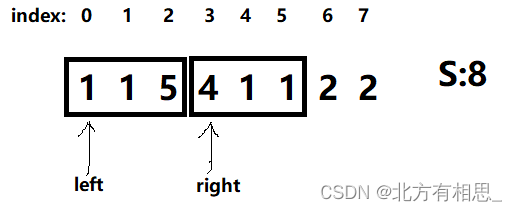
为什么各放两颗石头放不下,但是各放三颗石头放得下呢?问题就出在右半部分这里。当num递增的时候,右半部分会经历这样的变化:
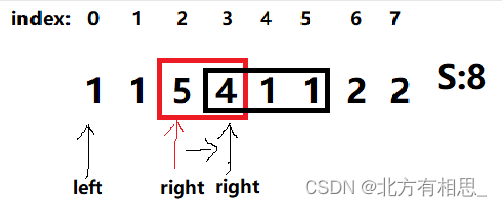
注意看,红色框表示的是num=2时,右半部分的石头,黑色框表示的是num=3时右半部分的石头。(right之所以移动了是因为right=left+num,num递增之后right自然也移动了,但left没有变化)右半部分变化前后相比,少了一个5,多了1 1。虽然石头数目增多了,但是石头重量反而减小了,这就可能会让原来大于S的总重量变得小于等于S。
那我们这样的思路就没有一点可取之处吗?我们该如何找到正确的思路呢?
反思一下上面的思路,当left不变时,随着num的增多,左半部分的总重量绝对是递增的,但是右半部分的总重量并不总是递增。那是不是说我们只需要找到一种方法,让左右部分的总重量总是递增,是不是就能得到正确的结果呢?
最终思路
下面,我将沿用上面的思路,但是修改部分细节。
请记住如下变量的含义:mid 分割左右部分的中心点。num为左半部分石头的数量(这也是右半部分石头的数量)leftWeight和rightWeight为左右部分的重量
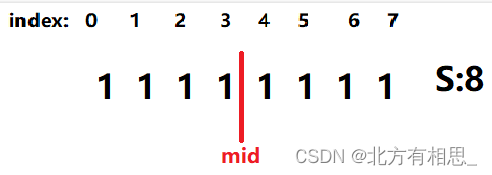
但是数组索引不可能为小数,我们不妨将mid移到它右边的那个索引。如图中,我们不妨将mid=4。
那么左半部分的石头为[mid-num , ... , mid-1],右半部分的石头为[mid , ... , mid+num-1]。
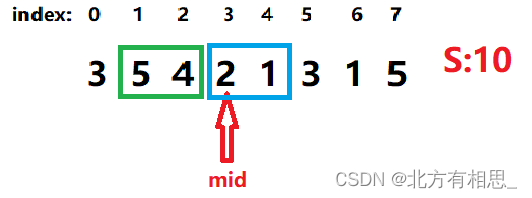
在上图,此时mid=3,num=2.那么左半部分的石头就是stone[1,2]即 5 4 ,右半部分石头为stone[3,4]即2 1。
可以看到,这个时候是满足题意的,那我们试探性的看看num能不能继续递增:
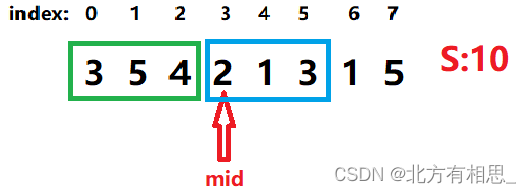
很明显,num不能为3.那我们只能保持num=2,将mid右移。
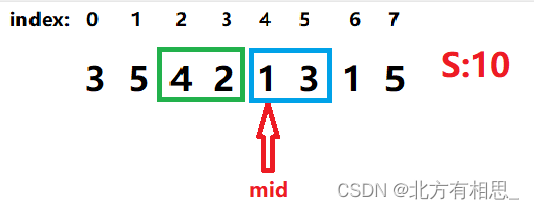
在mid=4,num=2的情况下,我们接着试探性递增一下num。
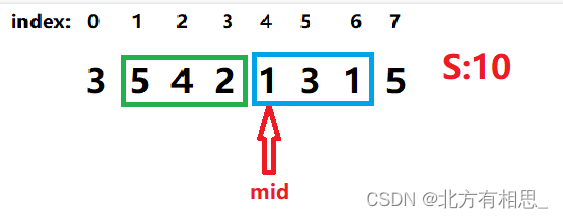
明显,依然不可以。那我们继续保持num=2,将mid继续右移。
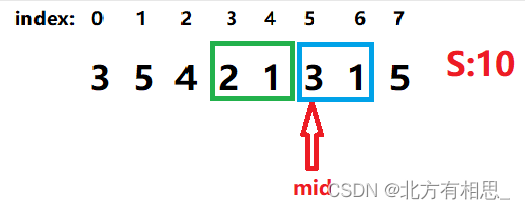
在mid=5,num=2的情况下,试探性递增num。
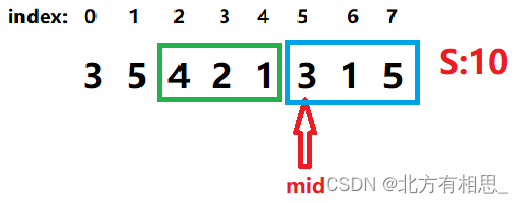
满足题意,那么我们就使num=3。
最后输出的答案依然是2*num。
至于leftWeight和rightWeight的更新,我们当然不用傻傻的每次都遍历数组求和。


当mid=4要变到mid=5的状态时(此时我们依旧先把mid视作为4)
我们仅需要进行如下操作
leftWeight=leftWeight-stone[mid-num]+stone[mid]
对于左半部分,我们仅需要减去最左边那颗石头的重量,然后再加上stone[mid](即将要加入左半部分的石头的重量)
rightWeight=rightWeight-stone[mid]+stone[mid+num]
对于右半部分,我们仅需要减去最左边那颗石头的重量,然后再加上stone[mid+num](即将要加入左半部分的石头的重量)
然后再将mid递增。(此时mid=5)
为什么这种思路是正确的呢(应该是正确的吧。。。哈哈哈。虽然能高效ac蓝桥杯上这道题,但我确实也不是很相信它的评测数据了呢)
当mid不变时,递增num。
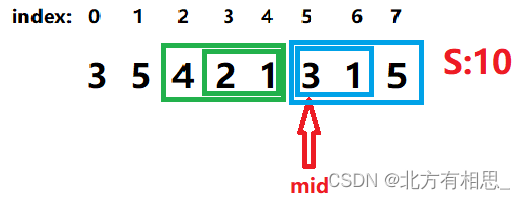
很显然,左右部分的重量绝对非递减(不说递增是因为石头重量貌似可以为0)
那么当num=n不能满足题意时,num=n+1一定也不能满足题意。
(之前的错误思路中,当left不变时,如果num=n不能满足题意,num=n+1反而有可能满足题意)。
上代码:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll N, S;
vector<ll> an;
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> N >> S;
an.resize(N+10);
for (ll i = 0; i < N; i++)cin >> an[i];
for (ll i = N; i < an.size(); i++)an[i] = 1e14;//边界,边界厚一点对性能影响也微乎其微嘛哈哈哈
ll num = 0;
ll mid = 1;
ll leftWeight = 0, rightWeight = 0;
for (; mid + num < N; mid++) {
for (; mid - num > 0;) {//mid-num>0:防止越界
if (leftWeight + an[mid - num - 1] <= S && rightWeight + an[mid + num] <= S) {//试探性递增num
//发现递增num之后依然可以满足题意
leftWeight += an[mid - num - 1];
rightWeight += an[mid + num];
num++;
}
else {
//发现当mid为此时这个状态的时候,num已经递增到极限了,不能再递增了,那么退出循环,让mid右移
break;
}
}
//num不变,mid右移,更新左右部分的重量
leftWeight = leftWeight - an[mid - num] + an[mid];
rightWeight = rightWeight - an[mid] + an[mid + num];
}
cout << 2*num;
}
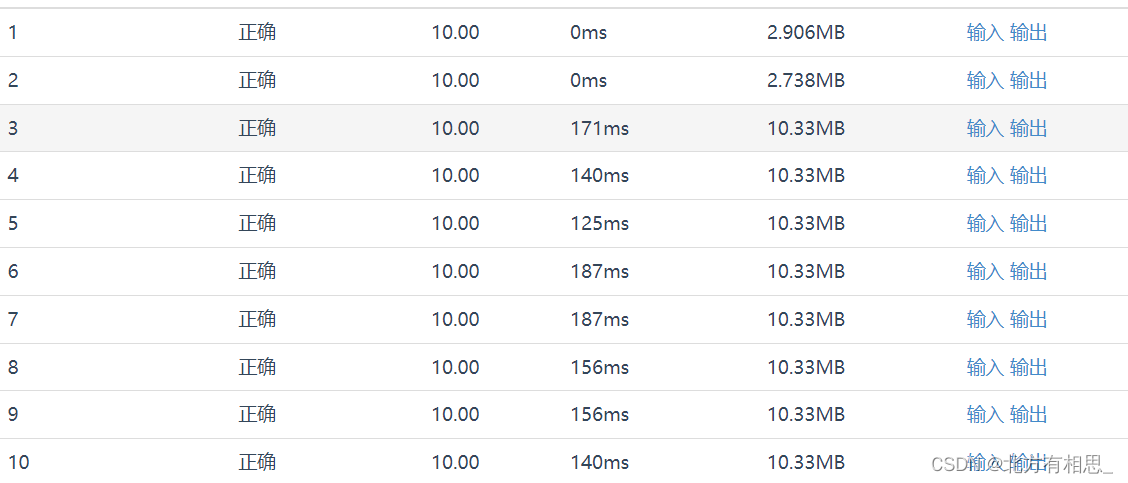
我们这个思路的时间复杂度应该是O(n)级的吧。。
毕竟无论是num递增还是mid递增,当mid+num碰触到最右边界的时候就结束了。速度还是很快的。
这里放一组网上其他的ac代码的性能,对比之下我这个代码的性能还是很可以的
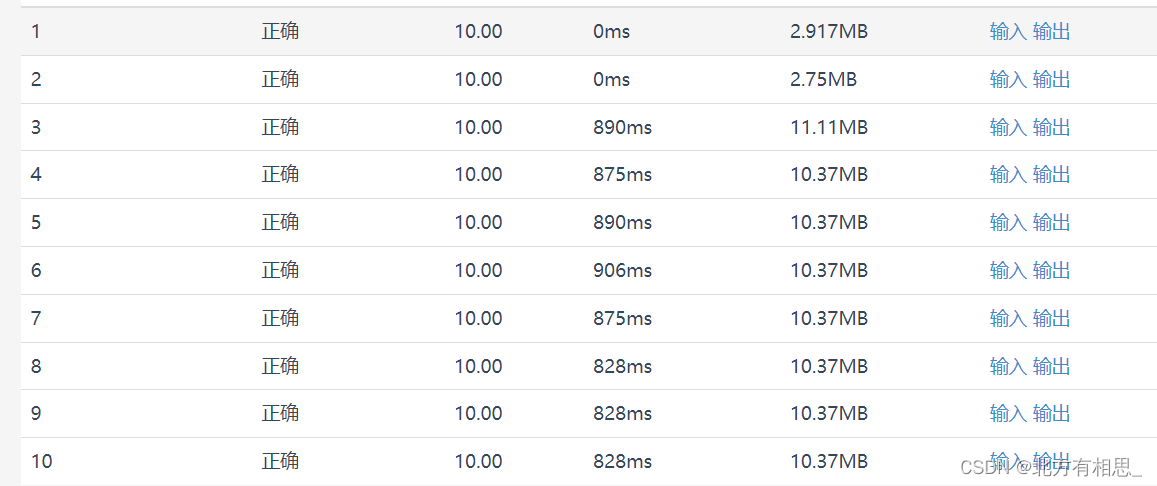
如果本文有谬误,烦请各位斧正,不胜言谢。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容










所有评论(0)