本文作者：Light Sea@知乎。未经作者允许，本文禁止转载，谢谢合作。

原论文题目《Deep unsupervised clustering with gaussian mixture variational autoencoders》。

本文我将介绍VAE针对无监督聚类的一个扩展：GMVAE，即基于高斯混合模型的VAE。我们在之前的文章中已经介绍了VAE，它是一个无监督的生成模型，其良好的性能和end-to-end的性质让它在深度学习时代被广泛应用。而GMVAE则将VAE的相关技术应用到无监督聚类问题上，其思想在于通过扩展latent variable structure提升VAE的聚类性能。

1. Introduction

无监督聚类一直是机器学习中比较重要的题目，传统方法例如我们熟知的k-means或者高斯混合模型(GMM)到现在仍然被广泛使用。但在深度学习快速发展的今天，作者希望可以借助深度学习的力量来提升这个问题的表现。

传统的deep generative model，例如VAE，并不是专门为了聚类而设计的。但是像VAE这样的深度生成模型中包含了一个重要的东西：latent variable。实际上潜变量建模了一些抽象的概念，潜变量的结构在某些时候就包含了类别信息。举个例子，如果我们使用MNIST数据来训练VAE，我们就能观察到不同种类数字的潜变量实际上在潜变量空间中形成了不同的cluster。

然而这样虽然有可能完成聚类，但却没有任何显式的能完成聚类的保证。另外，潜变量的先验分布很简单，因此不能建模复杂数据。因此在这篇文章中作者基于VAE设计了一个专门用于聚类的算法。算法假设数据生成于一个多模态(multimodal)的先验分布。作者构建了一个end-to-end的模型，从而可以用BP轻易更新整个网络。

2. Method

2.1 Generative and recognition models

作者选择混合高斯作为先验分布。我们考虑一个生成模型：

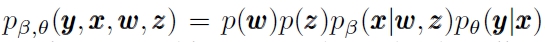
这里

对这几个潜变量有下面的假设：

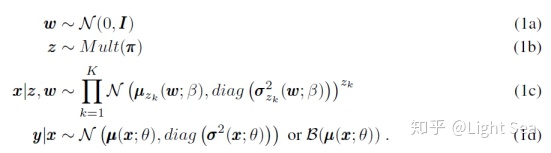
什么意思呢？模型首先从标准高斯分布中采样一个

假设随见变量

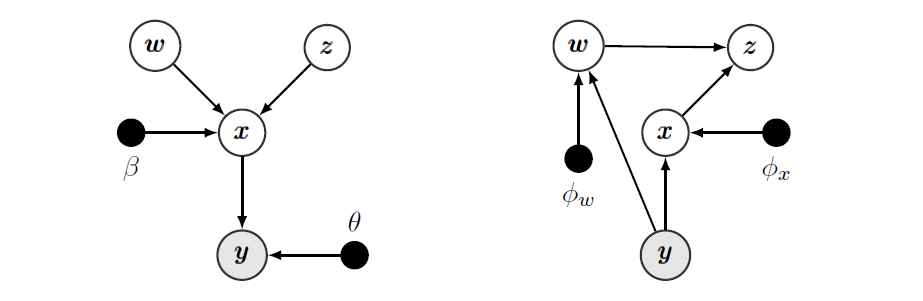
下图展示了这个模型的graphical model：

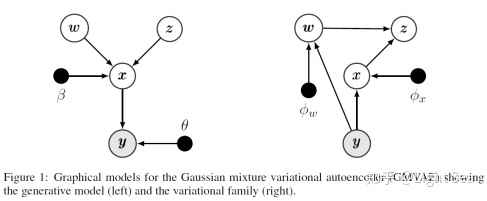
2.2 Inference with the recognition model

模型通过优化ELBO来训练：

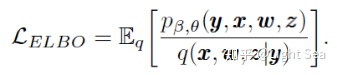
应用一些独立性假设，我们得到下面的分解：

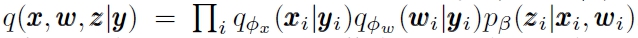
这里

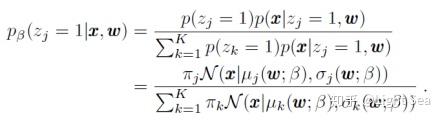
经过推导可以得到ELBO的简化表达式：

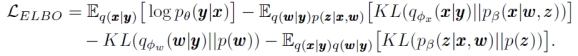
我们分别称上式右边的四个项为reconstruction term, conditional prior term,

我们分别讨论这几项。

这里Reconstruction term其实就是最常见的重构建损失，用相应的损失函数比如MSE就可以；而

我们重点看后面的几项，首先conditional prior term可以用下面的式子来估计：

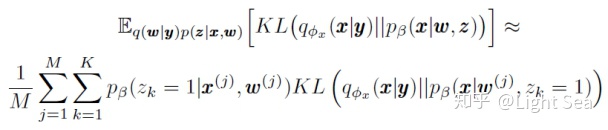
这里由于对于所有的

2.3 The over-regularization problem

所谓over-regularization problem是指ELBO中KL项被过度优化从而导致KL项迅速变为0的问题。这种情况下，latent variable会变得非常简单且不能很好的表示数据的结构。一般来说有两种办法解决这个问题。一是给KL项添加权重，边训练边增加权重；二是为KL项设置一个阈值，一旦它小于这个值就不再优化KL项。这里作者使用第二种方法来调整

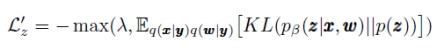
3. Experiment

作者一共做了三个部分的实验，一是在synthetic data上做的用来验证和解决over-regularization问题的实验；二是在MNIST上训练无监督聚类的实验；最后是用随机噪声生成图片的实验。

我们重点看后面两个实验。

3.1 Unsupervised image clustering

作者使用MNIST数据集进行无监督聚类，结果如下表所示：

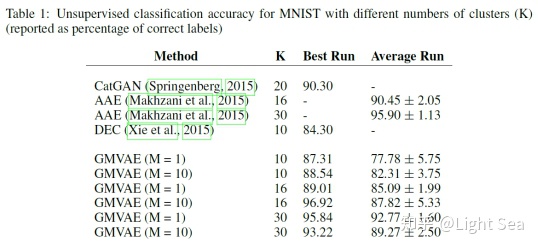
可以看到GMVAE的表现比之前的绝大多数方法要好，但要劣于adversarial auto-encoder(AAE)。

另外作者还观察到大的K和M能增加模型表现和稳定性，如下图所示：

3.2 Image generation

作者设置噪声w为0，然后在混合高斯的不同成分中采样来生成手写数字，结果发现不同成分对应了不同的数字，这就证明GMVAE成功地学习到了不同的类别。

作者还固定混合高斯的成分，然后改变噪声w，发现噪声w实际上控制了数字的风格。

这两个实验的结果如下图所示：

4. Conclusion

GMVAE改进了传统的VAE，使得latent variable structure更加复杂，从而能够更好的完成无监督聚类任务。作者提出的latent variable具有明显的层次结构，这就使得latent variable更易被理解，因此有更好的性能也就不足为奇了。

创作不易，如果各位感觉到有收获请点赞收藏支持一下，你的支持就是我创作的最大动力。