1.算法整体流程

输入：训练域为: $S$

初始化：模型参数$\theta$,学习率：$\beta ,\gamma$

for ite in iterations do

​ Split:$\bar{S}$ and $\check{S}$ $\to$ $S$

​ Meta-train:

​ Gradients ${\nabla }_{{\theta }_1}={\mathcal{F}}_{\theta }^{{}^{\prime }}(\bar{S};\theta )$

​ Updated parameters ${\theta }^{{}^{\prime }}=\theta -\beta {\nabla }_{{\theta }_1}$

​ Meta-test:

​ Loss is $\mathcal{G}(\check{S};{\theta }^{{}^{\prime }})$

​ Gradients Update $\theta :$
${\nabla }_{{\theta }_2}=\frac{d\mathcal{G}(\check{S};{\theta }^{{}^{\prime }})}{d\theta }=\frac{d\mathcal{G}(\check{S};\theta -\beta {\nabla }_{{\theta }_1})}{d{\theta }^{{}^{\prime }}}\frac{d{\theta }^{{}^{\prime }}}{d\theta }={\mathcal{G}}_{{\theta }^{{}^{\prime }}}^{{}^{\prime }}(\check{S};\theta -\beta {\nabla }_{{\theta }_1})\frac{d(\theta -\beta {\nabla }_{{\theta }_1})}{d\theta }={\mathcal{G}}_{{\theta }^{{}^{\prime }}}^{{}^{\prime }}(\check{S};\theta -\beta {\nabla }_{{\theta }_1})(1-\beta \frac{d{\nabla }_{{\theta }_1}}{d\theta })$

​ Meta-optimization: Update θ:csdn在线markdnow的latex不支持begin{align}标签，贴图如下\theta:{\color{Red}csdn在线markdnow的latex不支持begin\{align\}标签，贴图如下}θ:csdn在线markdnow的latex不支持begin{align}标签，贴图如下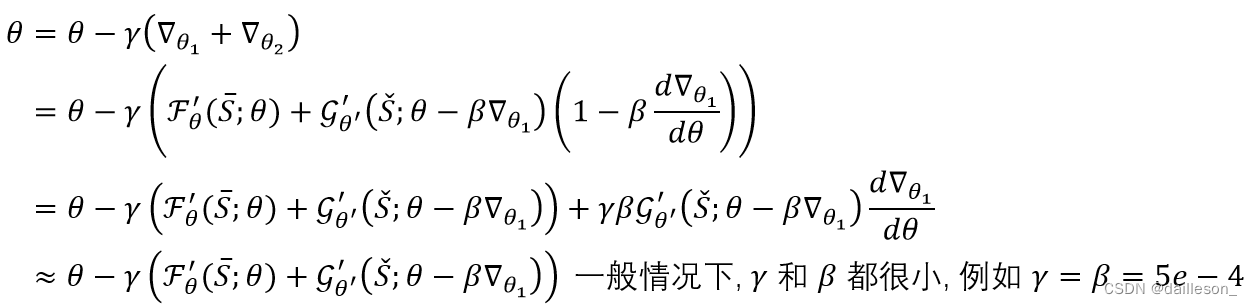

2.总结

MLDG是第一篇将meta learning引入domain generalization的论文。在这篇论文中，$\mathcal{G}(;)=\mathcal{F}(;)=CrossEntropy$，二阶导几乎不起作用，训练模型的时候可以将代码中二阶导计算关掉(没用还很耗时)。

loss.backward(retain_graph=True, create_graph=True)
->改为
loss.backward(retain_graph=True, create_graph=False)

楼主跑过这篇文章的代码，性能与普通训练方式差不太多，即先在$\bar{S}$训练更新，然后再在 $\check{S}$上训练更新。个人认为他的insight在于启发了后续的meta-dg方法，后续方法重新设计能够约束特征空间的$\mathcal{G}(;)$，后续方法是否有效等楼主验证后再更新。