学习笔记23--多传感器信息融合基础理论
本系列博客包括6个专栏,分别为:《自动驾驶技术概览》、《自动驾驶汽车平台技术基础》、《自动驾驶汽车定位技术》、《自动驾驶汽车环境感知》、《自动驾驶汽车决策与控制》、《自动驾驶系统设计及应用》,笔者不是自动驾驶领域的专家,只是一个在探索自动驾驶路上的小白,此系列丛书尚未阅读完,也是边阅读边总结边思考,欢迎各位小伙伴,各位大牛们在评论区给出建议,帮笔者这个小白挑出错误,谢谢!此专栏是关于《自动驾驶汽车
本系列博客包括6个专栏,分别为:《自动驾驶技术概览》、《自动驾驶汽车平台技术基础》、《自动驾驶汽车定位技术》、《自动驾驶汽车环境感知》、《自动驾驶汽车决策与控制》、《自动驾驶系统设计及应用》,笔者不是自动驾驶领域的专家,只是一个在探索自动驾驶路上的小白,此系列丛书尚未阅读完,也是边阅读边总结边思考,欢迎各位小伙伴,各位大牛们在评论区给出建议,帮笔者这个小白挑出错误,谢谢!
此专栏是关于《自动驾驶汽车环境感知》书籍的笔记
1.多传感器信息融合基础理论
1.1 概论
- 实现自动驾驶,需要多个传感器相互配合,共同构成自动驾驶汽车的感知系统;
- 在多传感器信息融合过程中,需要解决如下几个关键问题:
- 数据对准。 由于每个传感器观测到的数据都在各自的参考框架内,在对这些信息进行融合之前,必须将它们交换到同一时空框架中;由于时空配准导致的舍入误差必须得到相应的补偿;
- 传感器观测数据的不确定性。 由于传感器工作环境的不确定性,导致观测数据中有噪声成分,在融合过程中需要在最大程度上降低这些信息的不确定性;
- 数据关联。 数据关联问题广泛存在,需要解决单传感器时间域上的关联问题,以及多传感空间域上的关联问题,从而能够确定来源于同一目标源的数据;
- 不完整性、不一致以及虚假数据。 在多传感器信息融合系统中,对传感器接收到的量测数据有时会存在多种解释,称之为数据的不完整性;多传感器数据往往也会对观测环境做出不一致甚至相互矛盾的解释;
- 对车载系统的要求:
- 统一的同步时钟,保证传感器信息的时间一致性和正确性;
- 准确的多传感器标定,保证相同时间下不同传感器信息的空间一致性;
1.2 多传感器信息融合基础理论
1.2.1 多传感器信息融合概述
- 传感器数据融合是针对一个系统使用多种传感器这一特定问题提出的信息处理方法,可发挥多种传感器的联合优势,消除单一传感器的局限性;
- 把分布在不同位置的多个同类或不同类传感器所提供的数据资源加以综合,采用使计算机技术对其进行分析,加以互补,实现最佳协同效果,获得对被观测对象的一致性解释与描述,提高系统的容错性,从而提高系统决策、规划、反应的快速性和正确性,使系统获得更充分的信息;
- 使用多传感器融合技术优势:
- 提高系统感知的准确度。 多种传感器联合互补,可避免单一传感器的局限性,最大程度发挥各个传感器的优势,能同时获取被检测物体的多种不同特征信息,减少环境、噪声等干扰;
- 增加系统的感知维度,提高系统的可靠性和健壮性。 多传感器融合可带来一定的信息冗余度,即使某一个传感器出现故障,系统仍可在一定范围内继续正常工作,具有较高的容错性,增加系统决策的可靠性和置信度;
- 增强环境使用能力。 应用多传感器融合技术采集的信息具有明显的特征互补性,对空间和时间的覆盖范围更广,弥补了单一传感器对空间的分辨率和环境的语义不确定性。
- 有效减少成本。 融合可以实现多个价格低廉的传感器代替价格昂贵的传感器设备,在保证性能的基础上降低成本预算;
- 传感器融合过程:
- 多个传感器独立工作获得观测数据;
- 对各传感器数据(RGB图像、点云数据等)进行预处理;
- 对处理数据进行特征提取、变换,并对其进行模式识别处理,获取对观测对象的描述信息;
- 在数据融合中心按照一定的准则进行数据关联;
- 使用足够优化的算法对各传感器数据进行融合,获得对观测对象的一致性描述和解释。
1.2.2 多传感器融合结构
根据传感器信息在不同信息层次上的融合,将多传感器信息融合分为:Low-level融合、High-level融合和混合融合结构;
- Low-level融合:包括数据级融合和特征级融合,是一种集中式融合结构;
- High-level融合:一种决策级别融合,可以是集中式融合或者分布式融合;
- 混合融合结构:多种Low-level和High-level融合结构组合而成;
1.2.2.1 Low-level融合
Low-level融合体系结构是一种较低信息层次上的融合,是集中式融合结构;集中式融合结构将各传感器获得的原始数据直接送到数据融合中心,进行数据对准、数据关联、预测等,在传感器端不需要任何处理,可以实现实时融合。 集中式融合结构具有较高的融合精度,算法灵活,但对其处理器的要求高,计算量大,成本较高,数据流向单一,缺少底层传感器之间的信息交流,可靠性较低,实现难度较大;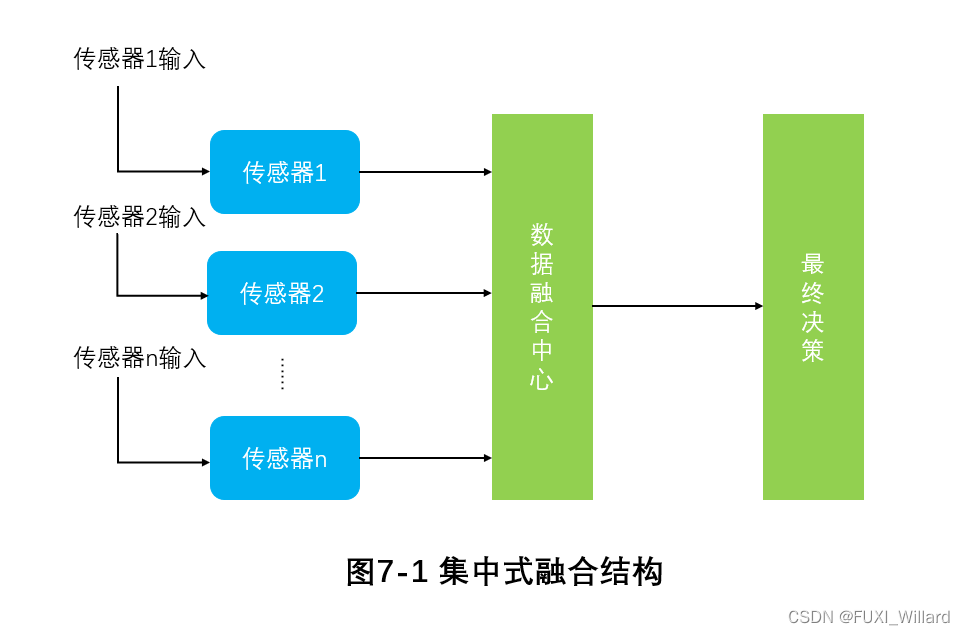
- 数据级融合
数据级融合又称为像素级融合,是最低层次的融合,直接对传感器的观测数据进行融合处理,然后基于融合后的结果进行特征提取和判断决策。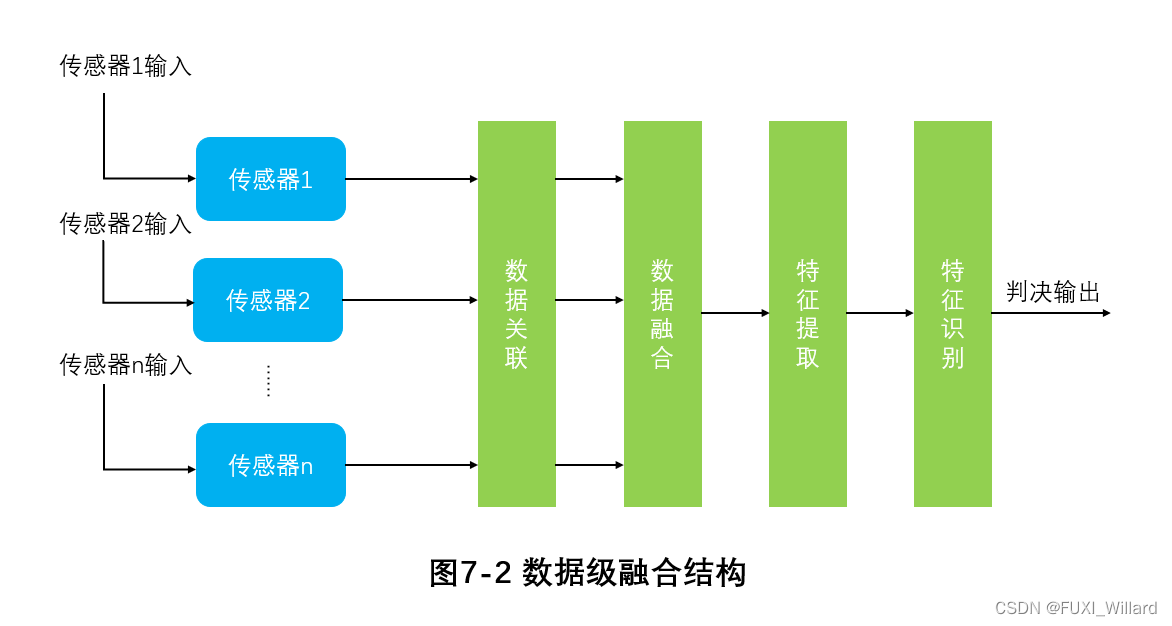
- 数据级融合处理的数据是最底层数据,精确到图像像素级别,但计算量大,处理所耗费的时间成本巨大,不利于实时处理;在进行数据通信时,容易受不稳定性、不确定性因素的影响;其处理过程都是在同种传感器下进行,无法有效地处理异构数据;
- 根据融合内容,数据级融合分为图像级融合、目标级融合和信号级融合。图像级融合以视觉为主体,将雷达输出的整体信息进行图像特征转化,与视觉系统的图像输出进行融合;目标级融合是对视觉和雷达的输出进行综合可信度加权,配合精度标定信息进行自适应的搜索匹配后融合输出;信号级融合是对视觉和雷达传感器ECU传出的数据源进行融合,其数据损失小,可靠性高,但需要大量的计算。
- 特征级融合
特征级融合指在提取所采集数据包含的特征向量之后融合。特征级融合通过各传感器的原始数据结合决策推理算法,对特征信息进行分类、汇集、综合,提取具有表示能力及统计信息的属性特征。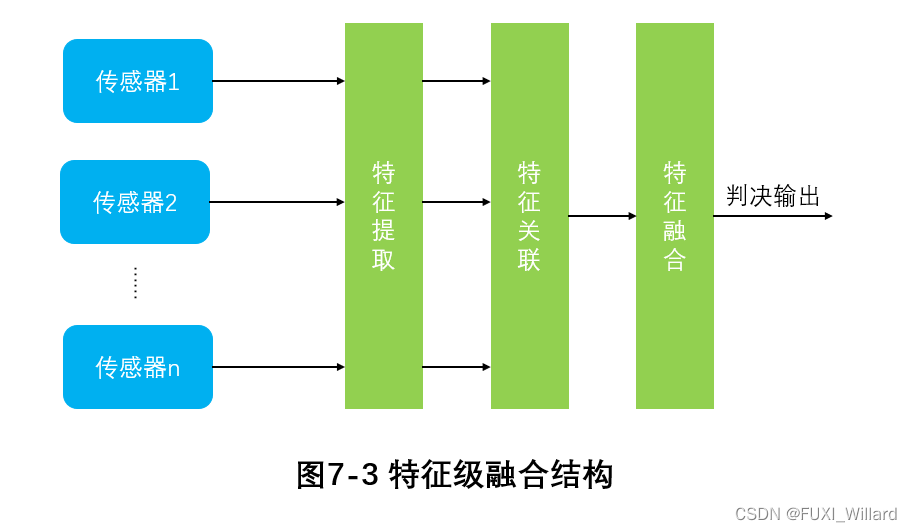
- 特征级融合先对图像信息进行压缩,再用计算机分析与处理,所消耗的内存、时间与数量级相对减少,因此处理的实时性会提高;
- 根据融合内容,特征级融合分为目标状态信息融合和目标特征融合;目标状态信息融合,先进行数据配准,以实现对状态和参数相关估计,更加适用于目标追踪;目标特征融合,借用传统模式识别技术,在特征预处理的前提下进行分类组合。
1.2.2.2 High-level融合
High-level融合体系结构是一种较高语义层次上的融合,可以是分布式融合结构或集中式融合结构;分布式融合结构在各独立节点都设置相应的处理单元,在对各个独立传感器所获得的原始数据进行局部处理的基础上,再将结果输入到数据融合中心,进行智能优化、组合、推理来获得最终的结果。 分布式融合结构计算速度快、延续性好,在某一传感器失灵的情况下仍可以继续工作,可靠性高;分布式融合结构对通信带宽需求低,适用于远距离传感器信息反馈,但在低通信带宽中传输会造成一定的损失,精度降低。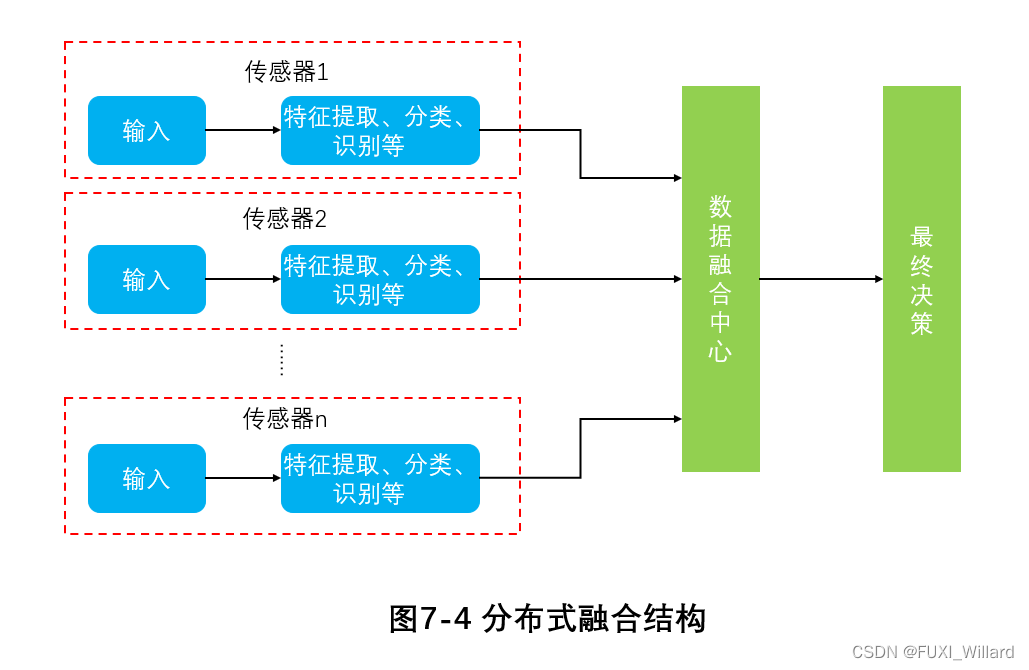
集中式融合结构,根据不同种类的传感器对同一目标观测的原始数据,进行一定的特征提取、分类、判别,以及简单的逻辑运算,然后根据应用需求进行较高级的决策,获得简明的综合推断结果,是高语义层次上的融合。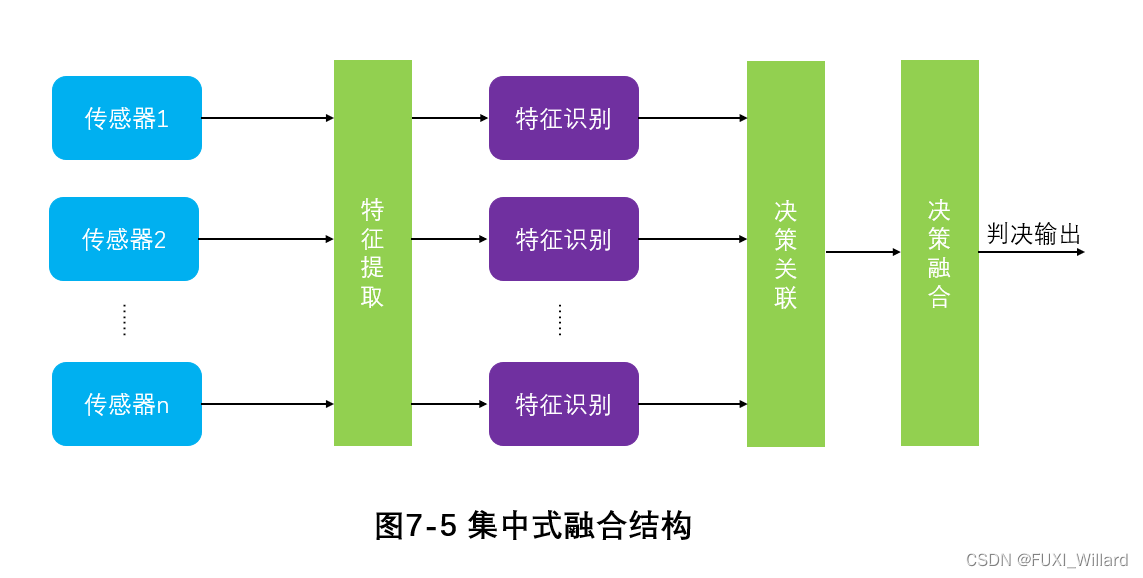
1.2.2.3 混合式融合结构
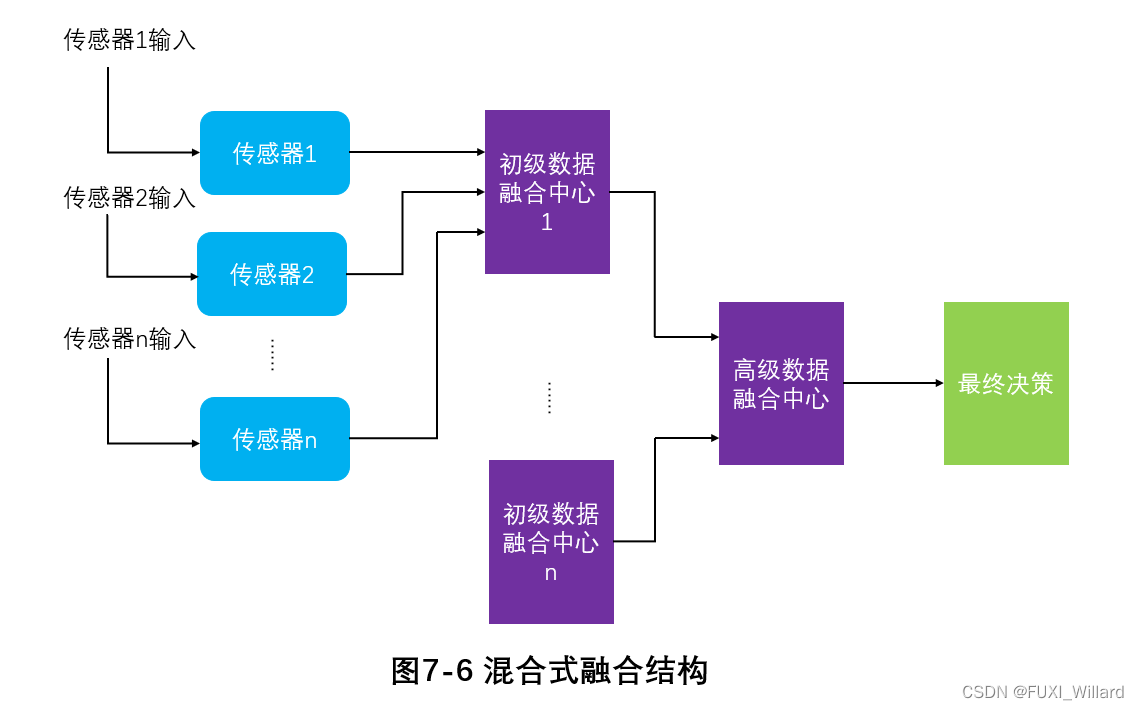
1.2.2.4 三种融合结构比较
| 体系结构 | 分布式 | 集中式 | 混合式 |
|---|---|---|---|
| 信息损失 | 大 | 小 | 中 |
| 精度 | 低 | 高 | 中 |
| 通信带宽 | 小 | 大 | 中 |
| 可靠性 | 高 | 低 | 高 |
| 计算速度 | 快 | 慢 | 中 |
| 可扩充性 | 好 | 差 | 一般 |
| 融合处理 | 容易 | 复杂 | 中等 |
| 融合控制 | 复杂 | 容易 | 中等 |
1.2.3 多传感器融合算法
多传感器融合常用算法:随机类和人工智能方法。随机类方法:卡尔曼滤波法(Kalman filtering),加权平均法、贝叶斯估计法(Bayesian estimation)、D-S(Dempster-Shafer)证据理论等;人工智能方法:专家系统、模糊逻辑理论、人工神经网络、遗传算法等;
1.2.3.1 随机类方法
-
加权平均法
加权平均法简单、直观,根据多个传感器独立探测的数据,乘上相应的权值,累加求和并取平均值,将其结果作为融合值。 -
贝叶斯估计法
贝叶斯估计法由Thomas Bayes提出,基于先验概率,并不断结合新的数据信息来得到新的概率;贝叶斯估计法常用于静态环境下特征层的融合,主要公式为:
P(Ai∣B)=P(B∣Ai)P(Ai)∑i=1nP(B∣Ai)P(Ai) P(A_i|B)=\frac{P(B|A_i)P(A_i)}{\sum_{i=1}^nP(B|A_i)P(A_i)} P(Ai∣B)=∑i=1nP(B∣Ai)P(Ai)P(B∣Ai)P(Ai)
贝叶斯估计法局限性在于其工作基于先验概率,若没有先验概率,则需要通过大量的数据统计来实现,往往需要耗费大量的时间和精力。 -
D-S证据理论
D-S证据理论是贝叶斯估计的扩展,是一种用于决策层的信息融合方法,三个基本要素:基本概率赋值函数、信任函数和似然函数。D-S证据理论不要求在未知情况下对每个事件进行单独赋值,仅将信任值赋给信任项,先将所有不确定时间都归为未知命题,然后通过证据组合来不断缩小未知的范围,直到达到判决条件。 -
卡尔曼滤波法
卡尔曼滤波法是一种利用线性状态方法,通过系统输入输出观测数据,对系统状态进行最优估计的算法;卡尔曼滤波法本质是最小均方误差准则下的最优线性估计。
估计:根据测量得出的跟目前的状态x(t)有关的数据z(t)=h[x(t)]+v(t)解算出x(t)的计算值x^(t),其中随机向量v(t)称为量测误差,x^(t)称为x(t)的估计,z(t)称为x(t)的量测。因为x^(t)是根据z(t)确定的,所以x^(t)是z(t)的函数;如果x^(t)是z(t)的线性函数,则x^(t)称为x(t)的线性估计。估计:根据测量得出的跟目前的状态x(t)有关的数据z(t)=h[x(t)]+v(t)解算出x(t)的计算值\hat{x}(t),\\其中随机向量v(t)称为量测误差,\hat{x}(t)称为x(t)的估计,z(t)称为x(t)的量测。\\因为\hat{x}(t)是根据z(t)确定的,所以\hat{x}(t)是z(t)的函数;如果\hat{x}(t)是z(t)的线性函数,则\hat{x}(t)称为x(t)的线性估计。估计:根据测量得出的跟目前的状态x(t)有关的数据z(t)=h[x(t)]+v(t)解算出x(t)的计算值x^(t),其中随机向量v(t)称为量测误差,x^(t)称为x(t)的估计,z(t)称为x(t)的量测。因为x^(t)是根据z(t)确定的,所以x^(t)是z(t)的函数;如果x^(t)是z(t)的线性函数,则x^(t)称为x(t)的线性估计。
设在[t0,t1]时间段内的量测为z(t),与之对应的估计为x^(t),则有三种对应关系:设在[t_0,t_1]时间段内的量测为z(t),与之对应的估计为\hat{x}(t),则有三种对应关系:设在[t0,t1]时间段内的量测为z(t),与之对应的估计为x^(t),则有三种对应关系:- 若t=t1,则x^(t)称为x(t)的估计若t=t_1,则\hat{x}(t)称为x(t)的估计若t=t1,则x^(t)称为x(t)的估计;
- 若t>t1,则x^(t)称为x(t)的预测若t>t_1,则\hat{x}(t)称为x(t)的预测若t>t1,则x^(t)称为x(t)的预测;
- 若t<t1,则x^(t)称为x(t)的平滑若t<t_1,则\hat{x}(t)称为x(t)的平滑若t<t1,则x^(t)称为x(t)的平滑。
最优估计:指某一指标函数达到最值时的估计;若以量测估计z(t)的偏差的平方和达到最小为指标,即最优估计:指某一指标函数达到最值时的估计;若以量测估计z(t)的偏差的平方和达到最小为指标,即最优估计:指某一指标函数达到最值时的估计;若以量测估计z(t)的偏差的平方和达到最小为指标,即:
min(z−z^)T(z−z^) \min(z-\hat{z})^T(z-\hat{z}) min(z−z^)T(z−z^)
则所得估计x^(t)称为x(t)的最小二乘估计则所得估计\hat{x}(t)称为x(t)的最小二乘估计则所得估计x^(t)称为x(t)的最小二乘估计
minE((x−x^)T(x−x^)) \min{E((x-\hat{x})^T(x-\hat{x}))} minE((x−x^)T(x−x^))
若x^(t)又为x(t)的线性估计,则x^(t)称为x(t)的线性最小方差估计。若\hat{x}(t)又为x(t)的线性估计,则\hat{x}(t)称为x(t)的线性最小方差估计。若x^(t)又为x(t)的线性估计,则x^(t)称为x(t)的线性最小方差估计。
最小二乘估计:适用于对随机向量或常值向量的估计,其达到的最优指标是使量测估计的精度达到最佳;最小方差估计:使均方差最小的估计,是估计方法中精度最高的。最小二乘估计:适用于对随机向量或常值向量的估计,其达到的最优指标是使量测估计的精度达到最佳;\\最小方差估计:使均方差最小的估计,是估计方法中精度最高的。最小二乘估计:适用于对随机向量或常值向量的估计,其达到的最优指标是使量测估计的精度达到最佳;最小方差估计:使均方差最小的估计,是估计方法中精度最高的。-
线性离散卡尔曼滤波方程
设tk时刻,随机离散系统状态方程为:设t_k时刻,随机离散系统状态方程为:设tk时刻,随机离散系统状态方程为:
Xk=Φk,k−1Xk−1+Γk−1Wk−1 X_k=\Phi_{k,k-1}X_{k-1}+\Gamma_{k-1}W_{k-1} Xk=Φk,k−1Xk−1+Γk−1Wk−1
相应的量测方程:相应的量测方程:相应的量测方程:
Zk=HkXk+Vk Z_k=H_kX_k+V_k Zk=HkXk+Vk
参数说明参数说明参数说明:- Xk:表示tk时刻的被估计状态;X_k:表示t_k时刻的被估计状态;Xk:表示tk时刻的被估计状态;
- Φk,k−1:tk−1时刻到tk时刻系统的n×n维状态转移矩阵;\Phi_{k,k-1}:t_{k-1}时刻到t_k时刻系统的n\times{n}维状态转移矩阵;Φk,k−1:tk−1时刻到tk时刻系统的n×n维状态转移矩阵;
- Γk−1:表示tk−1时刻系统n×p维噪声驱动矩阵;\Gamma_{k-1}:表示t_{k-1}时刻系统n\times{p}维噪声驱动矩阵;Γk−1:表示tk−1时刻系统n×p维噪声驱动矩阵;
- Wk−1:表示tk−1时刻系统激励噪声;W_{k-1}:表示t_{k-1}时刻系统激励噪声;Wk−1:表示tk−1时刻系统激励噪声;
- Zk:表示tk时刻的量测量;Z_k:表示t_k时刻的量测量;Zk:表示tk时刻的量测量;
- Hk:表示tk时刻的m×n维量测矩阵;H_k:表示t_k时刻的m\times{n}维量测矩阵;Hk:表示tk时刻的m×n维量测矩阵;
- Vk:表示tk时刻的量测噪声;V_k:表示t_k时刻的量测噪声;Vk:表示tk时刻的量测噪声;
系统激励噪声Wk和量测噪声Vk应具有如下性质:系统激励噪声W_k和量测噪声V_k应具有如下性质:系统激励噪声Wk和量测噪声Vk应具有如下性质:
{E[Wk]=0E[Vk]=0Cov[Wk,Vj]=E[WkVjT]=0Cov[Wk,Vj]=E[WkVjT]=QkδkjCov[Vk,Vj]=E[VkVjT]=Rkδkj \begin{cases} E[W_k]=0\\ E[V_k]=0\\ Cov[W_k,V_j]=E[W_kV_j^T]=0\\ Cov[W_k,V_j]=E[W_kV_j^T]=Q_k\delta_{kj}\\ Cov[V_k,V_j]=E[V_kV_j^T]=R_k\delta_{kj} \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧E[Wk]=0E[Vk]=0Cov[Wk,Vj]=E[WkVjT]=0Cov[Wk,Vj]=E[WkVjT]=QkδkjCov[Vk,Vj]=E[VkVjT]=Rkδkj
Qk、Rk:系统噪声的非负定方差矩阵和量测噪声的正定方差阵非负定的;Q_k、R_k:系统噪声的非负定方差矩阵和量测噪声的正定方差阵非负定的;Qk、Rk:系统噪声的非负定方差矩阵和量测噪声的正定方差阵非负定的;
δkj:克罗内克函数\delta_{kj}:克罗内克函数δkj:克罗内克函数;
假设Xk和Zk能分别满足上述状态方程和相对应的量测方程,Wk和Vk能同时满足上式,则k时刻Xk的最优估计值X^k可由以下方程递推得到:假设X_k和Z_k能分别满足上述状态方程和相对应的量测方程,W_k和V_k能同时满足上式,\\则k时刻X_k的最优估计值\hat{X}_k可由以下方程递推得到:假设Xk和Zk能分别满足上述状态方程和相对应的量测方程,Wk和Vk能同时满足上式,则k时刻Xk的最优估计值X^k可由以下方程递推得到:
X^k,k−1=Φk,k−1Xk−1 \hat{X}_{k,k-1}=\Phi_{k,k-1}X_{k-1} X^k,k−1=Φk,k−1Xk−1 -
状态估计
X^k=X^k,k−1+Kk(Zk−HkX^k,k−1) \hat{X}_k=\hat{X}_{k,k-1}+K_k(Z_k-H_k\hat{X}_{k,k-1}) X^k=X^k,k−1+Kk(Zk−HkX^k,k−1)
滤波增益矩阵:滤波增益矩阵:滤波增益矩阵:
Kk=Pk,k−1HkT(HkPk,k−1HkT+Rk)−1 K_k=P_{k,k-1}H_k^T(H_kP_{k,k-1}H_k^T+R_k)^{-1} Kk=Pk,k−1HkT(HkPk,k−1HkT+Rk)−1
或或或
Hk=PkHkTPk−1H_k=P_kH_k^TP_k^{-1}Hk=PkHkTPk−1
进一步预测误差矩阵:进一步预测误差矩阵:进一步预测误差矩阵:
Pk,k−1=Φk,k−1Pk−1Φk,k−1T+Γk−1Qk−1Γk−1T P_{k,k-1}=\Phi_{k,k-1}P_{k-1}\Phi_{k,k-1}^T+\Gamma_{k-1}Q_{k-1}\Gamma_{k-1}^T Pk,k−1=Φk,k−1Pk−1Φk,k−1T+Γk−1Qk−1Γk−1T
估计均方误差:估计均方误差:估计均方误差:
Pk=(I−KkHk)Pk,k−1(I−KkHk)T+KkRkKkT P_k=(I-K_kH_k)P_{k,k-1}(I-K_kH_k)^T+K_kR_kK_k^T Pk=(I−KkHk)Pk,k−1(I−KkHk)T+KkRkKkT
或或或
Pk=(I−KkHk)Pk,k−1 P_k=(I-K_kH_k)P_{k,k-1} Pk=(I−KkHk)Pk,k−1
或或或
Pk−1=Pk,k−1−1+HkTRk−1Hk P_k^{-1}=P_{k,k-1}^{-1}+H_k^TR_k^{-1}H_k Pk−1=Pk,k−1−1+HkTRk−1Hk
以上几个公式是离散型卡尔曼滤波的基本方程;在假定已知系统初始估计值X^0和初始估计均方差阵P0的条件下,再结合tk时刻的量测量Zk可以利用卡尔曼滤波方程得到系统tk时刻的状态估计X^k以上几个公式是离散型卡尔曼滤波的基本方程;在假定已知系统初始估计值\hat{X}_0和初始估计均方差阵P_0\\的条件下,再结合t_k时刻的量测量Z_k可以利用卡尔曼滤波方程得到系统t_k时刻的状态估计\hat{X}_k以上几个公式是离散型卡尔曼滤波的基本方程;在假定已知系统初始估计值X^0和初始估计均方差阵P0的条件下,再结合tk时刻的量测量Zk可以利用卡尔曼滤波方程得到系统tk时刻的状态估计X^k。
1.2.3.2 人工智能方法
- 模糊逻辑理论
模糊逻辑理论基于多值逻辑,实质是将一个给定输入空间通过模糊逻辑的方法映射到一个特定输出空间的计算过程,比较适合高层次上的融合,如决策级融合;模糊逻辑推理对信息的描述具有较大的主观因素,信息的表示缺乏客观性;其计算量较大,计算过程较为复杂,实时性不高; - 人工神经网络
神经网络具有很强的容错性,很强的自学习、自组织及非线性映射能力,能够模拟复杂的非线性映射;
更多推荐
 已为社区贡献31条内容
已为社区贡献31条内容








所有评论(0)