NASH:基于丰富网络态射和爬山算法的神经网络架构搜索 | ICLR 2018
论文提出NASH方法来进行神经网络结构搜索,核心思想与之前的EAS方法类似,使用网络态射来生成一系列效果一致且继承权重的复杂子网,本文的网络态射更丰富,而且仅需要简单的爬山算法辅助就可以完成搜索,耗时0.5GPU day 来源:晓飞的算法工程笔记 公众号论文: Simple And Efficient Architecture Search for Convolutional Neural Net
论文提出NASH方法来进行神经网络结构搜索,核心思想与之前的EAS方法类似,使用网络态射来生成一系列效果一致且继承权重的复杂子网,本文的网络态射更丰富,而且仅需要简单的爬山算法辅助就可以完成搜索,耗时0.5GPU day
来源:晓飞的算法工程笔记 公众号
论文: Simple And Efficient Architecture Search for Convolutional Neural Networks

Introduction
论文目标在于大量减少网络搜索的计算量并保持结果的高性能,核心思想与EAS算法类似,主要贡献如下:
- 提供baseline方法,随机构造网络并配合SGDR进行训练,在CIFAR-10上能达到6%-7%的错误率,高于大部分NAS方法。
- 拓展了EAS在网络态射(network morphisms)上的研究,能够提供流行的网络构造block,比如skip connection和BN。
- 提出基于爬山算法的神经网络结构搜索NASH,该方法迭代地进行网络搜索,在每次迭代中,对当前网络使用一系列网络态射得到多个新网络,然后使用余弦退火进行快速优化,最终得到性能更好的新网络。在CIFAR-10上,NASH仅需要单卡12小时就可以达到baseline的准确率。
Network Morphism
N ( X ) \mathcal{N}(\mathcal{X}) N(X)为 X ∈ R n \mathcal{X}\in \mathbb{R}^n X∈Rn上的一系列网络,网络态射(network morphism)为映射 M : N ( X ) × R k → N ( X ) × R j M: \mathcal{N}(\mathcal{X}) \times \mathbb{R}^k \to \mathcal{N}(\mathcal{X}) \times \mathbb{R}^j M:N(X)×Rk→N(X)×Rj,从参数为 w ∈ R k w\in \mathbb{R}^k w∈Rk的网络 f w ∈ N ( X ) f^w \in \mathcal{N}(\mathcal{X}) fw∈N(X)转换为参数为 w ~ ∈ R j \tilde{w} \in \mathbb{R}^j w~∈Rj的网络KaTeX parse error: Got function '\tilde' with no arguments as superscript at position 3: g^\̲t̲i̲l̲d̲e̲{w} \in \mathca…,并且满足公式1,即对于相同的输入,网络的输出不变。
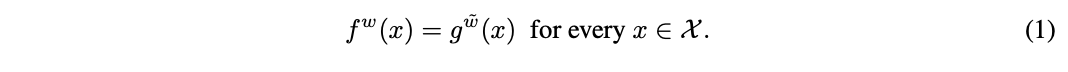
下面给出几种标准网络结构的网络态射例子:
Network morphism Type I
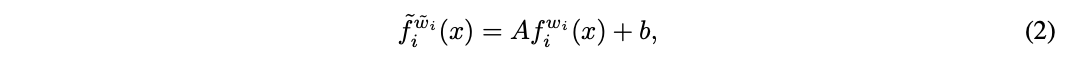
将 f w f^w fw进行公式2的替换, w ~ = ( w i , C , d ) \tilde{w}=(w_i, C, d) w~=(wi,C,d),为了满足公式1,设定 A = 1 A=1 A=1和 b = 0 b=0 b=0,可用于添加全连接层。
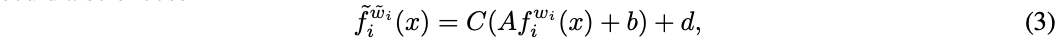
另外一种复杂点的策略如公式3, w ~ = ( w i , C , d ) \tilde{w}=(w_i, C, d) w~=(wi,C,d),设定 C = A − 1 C=A^{-1} C=A−1和 d = − C b d=-Cb d=−Cb,可用于表达BN层,其中 A A A和 b b b表示统计结构, C C C和 d d d为可学习的 γ \gamma γ和 β \beta β。
Network morphism Type II
假设 f i w i f_i^{w_i} fiwi可由任何函数 h h h表示,即 f i w i = A h w h ( x ) + b f_i^{w_i}=Ah^{w_h}(x)+b fiwi=Ahwh(x)+b
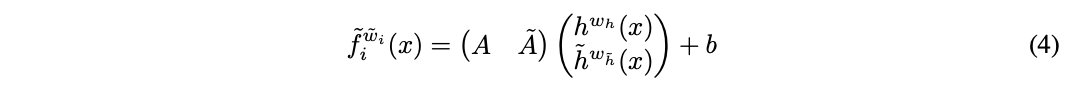
则可以将 f w f^w fw, w i = ( w h , A , b ) w_i = (w_h, A, b) wi=(wh,A,b)配合任意函数 h ~ w h ~ ( x ) \tilde{h}^{w_{\tilde{h}}}(x) h~wh~(x)根据公式4替换为 f ~ w ~ i \tilde{f}^{\tilde{w}_i} f~w~i, w ~ = ( w i , w h ~ , A ~ ) \tilde{w}=(w_i, w_{\tilde{h}}, \tilde{A}) w~=(wi,wh~,A~),设定 A ~ = 0 \tilde{A}=0 A~=0。这个态射可以表示为两种结构:
- 增加层宽度,将 h ( x ) h(x) h(x)想象为待拓宽的层,设定 h ~ = h \tilde{h}=h h~=h则可以增加两倍的层宽度。
- concatenation型的skip connection,假设 h ( x ) h(x) h(x)本身就是一系列层操作 h ( x ) = h n ( x ) ∘ ⋯ ∘ h 0 ( x ) h(x)=h_n(x) \circ \cdots \circ h_0(x) h(x)=hn(x)∘⋯∘h0(x),设定 h ~ ( x ) = x \tilde{h}(x)=x h~(x)=x来实现短路连接。
Network morphism Type III
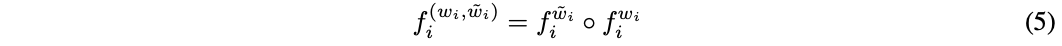
任何幂等的函数 f i w i f_i^{w_i} fiwi都可以通过公式5进行替换,初始化 w ~ i = w i \tilde{w}_i=w_i w~i=wi,公式5在无权重的幂等函数上也成立,比如ReLU。
Network morphism Type IV
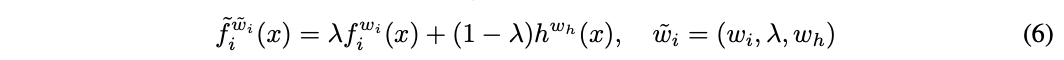
任何层 f i w i f_i^{w_i} fiwi都可以配合任意函数 h h h进行公式6的替换,初始化 λ = 1 \lambda=1 λ=1,可用于结合任意函数,特别是非线性函数,也可以用于加入additive型的skip connection。
此外,不同的网络态射组合也可以产生新的态射,比如可以通过公式2、3和5在ReLU层后面插入"Conv-BatchNorm-Relu"的网络结构。
Architecture Search by Network Morphisms
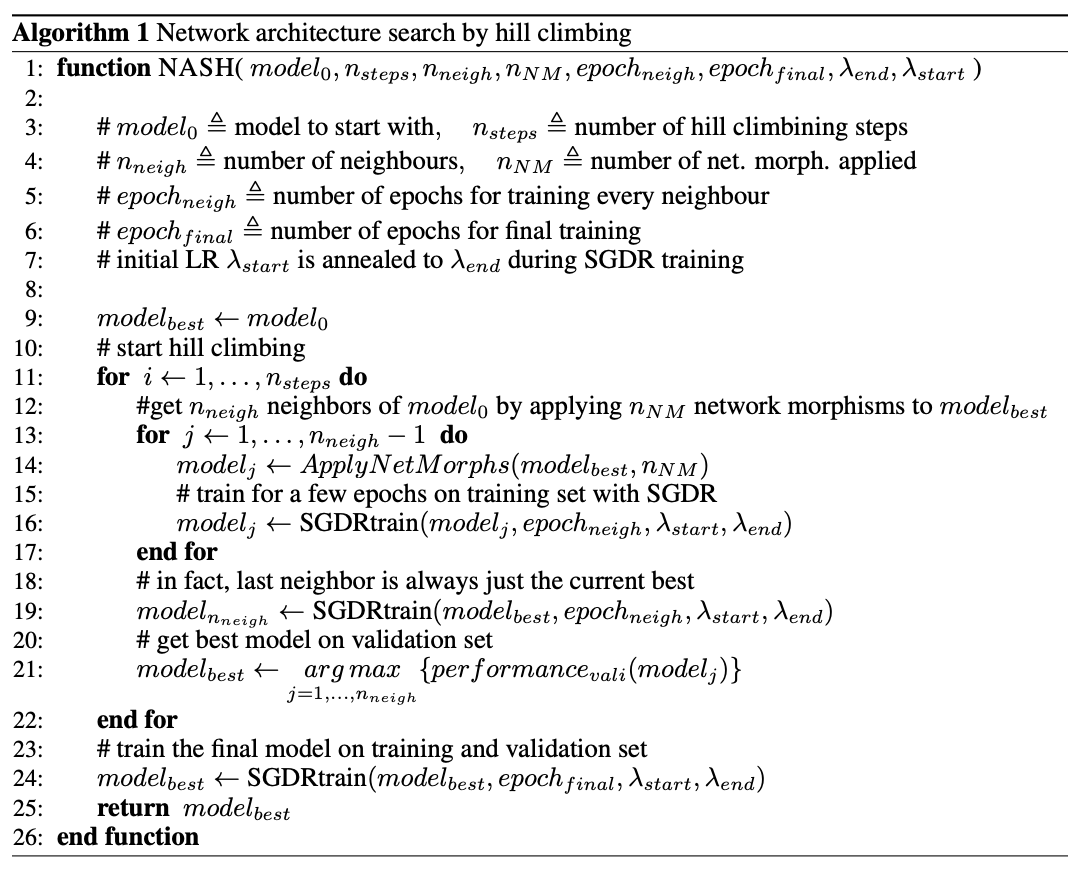
NASH方法基于爬山算法,先从小网络开始,对其进行网络态射生成更大的子网络,由于公式1的约束,子网的性能与原网络是一样的,后续子网进行简单的训练看是否有更好的性能,最后选择性能优异的子网进行重复的操作。
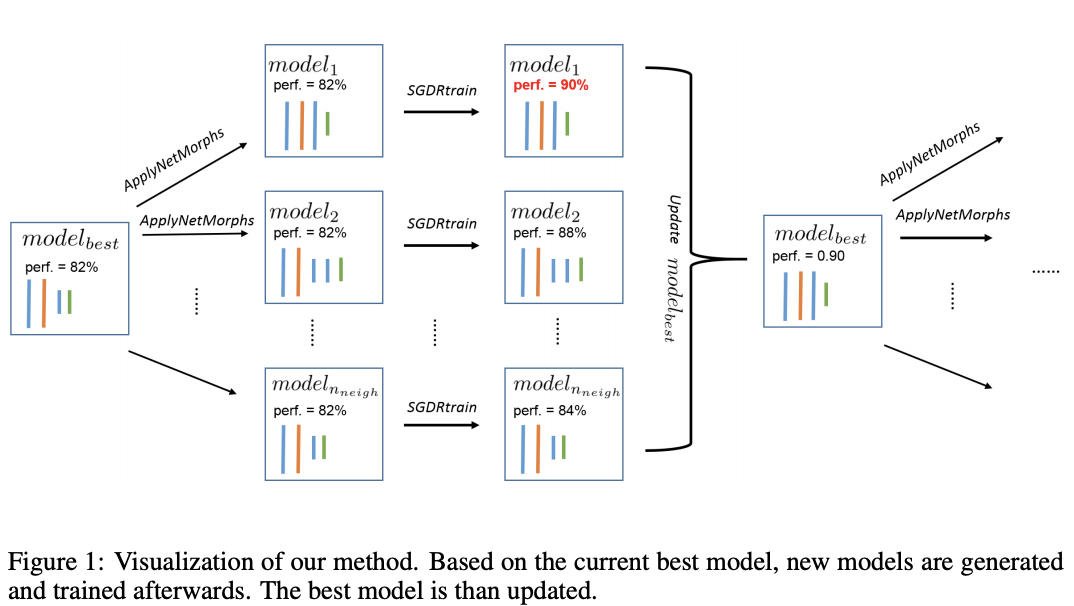
图1可视化了NASH方法的一个step,算法1的ApplyNetMorph(model, n)包含n个网络态射操作,每个为以下方法的随机一种:
- 加深网络,例如添加Conv-BatchNorm-Relu模块,插入位置和卷积核大小都是随机的,channel数量跟最近的卷积操作一致。
- 加宽网络,例如使用network morphism type II来加宽输出的channel,加宽比例随机。
- 添加从层 i i i到层 j j j的skup connection,使用network morphism type II或IV,插入位置均随机选择。
由于使用了网络态射,子网继承了原网络的权重且性能一致,NASH方法优势在于能够很快的评估子网的性能,论文使用了简单的爬山算法,当然也可以选择其它的优化策略。
Experiments
Baslines

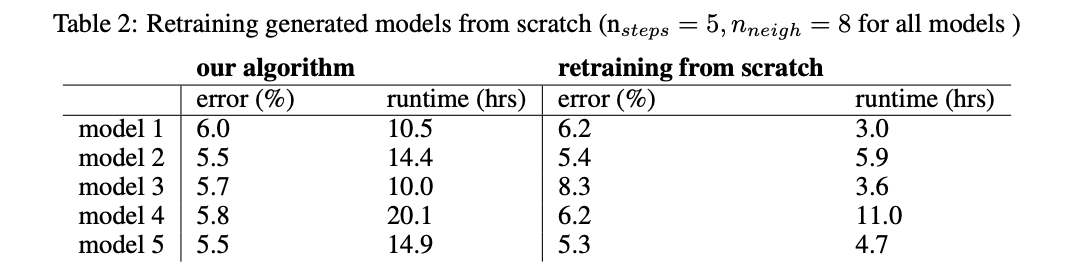
Retraining from Scratch
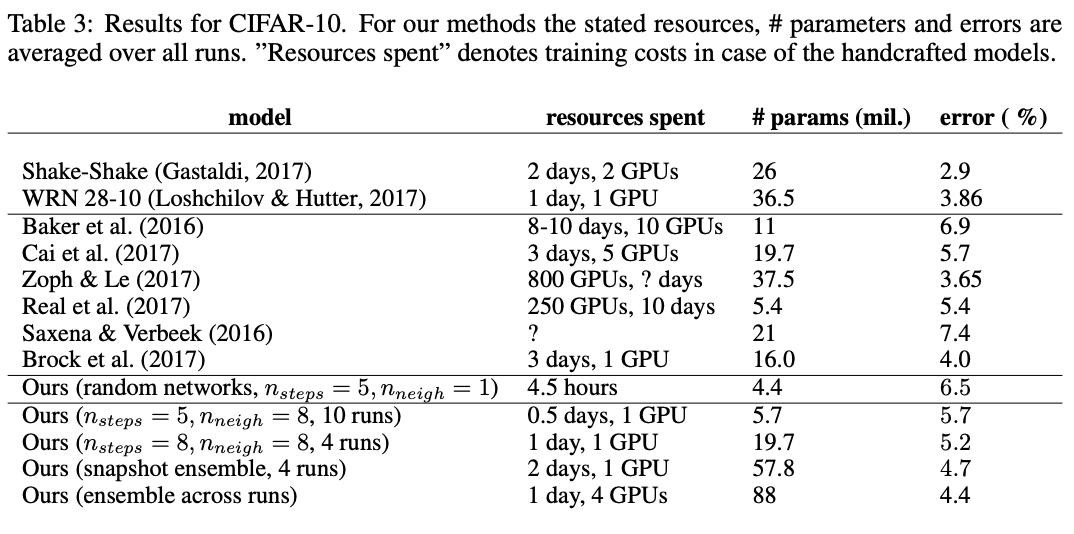
CIFAR-10
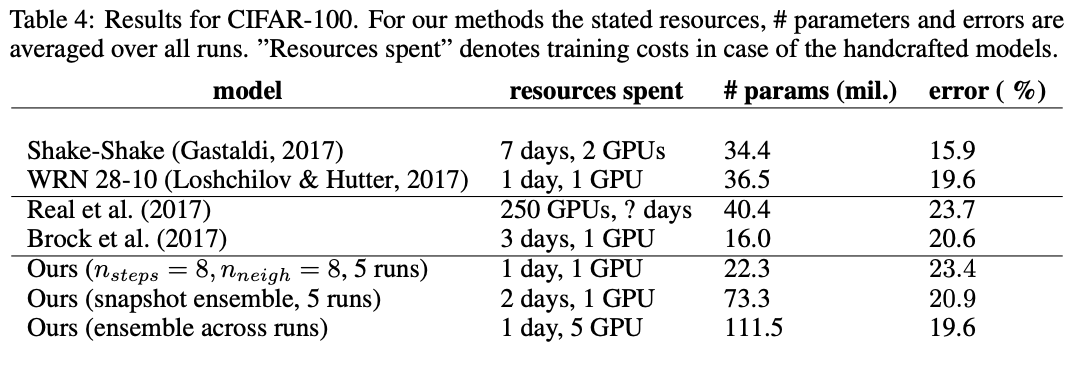
CIFAR-100
CONCLUSION
论文提出NASH方法来进行神经网络结构搜索,核心思想与之前的EAS方法类似,使用网络态射来生成一系列效果一致且继承权重的复杂子网,本文的网络态射更丰富,而且仅需要简单的爬山算法辅助就可以完成搜索,耗时0.5GPU day
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】

更多推荐
 已为社区贡献17条内容
已为社区贡献17条内容







所有评论(0)