目录

一、二分类

二、逻辑回归（Logistic回归）

2.1 怎么通过计算输出概率呢？

2.1.1 线性回归模型

2.1.2 逻辑回归模型

2.1.3总结：

2.2 损失函数和成本函数

2.2.1 损失函数（Loss Function）

 2.2.2 成本函数（Cost Function）

2.2.3 总结

 2.3 梯度下降法

三、手写笔记

---

一、二分类

通俗来说，二分类问题的类别标签label只有两种取值，0或1（有时候是-1或1)。

例如：

Input:一张图片----------->>Output:标签值1（是猫）  

我们输入的是一张猫的图片，希望得到的结果是机器识别出这是猫，标签label用1来表示是猫。

 假设这张图片的像素点是64*64，因为图片的色彩模式是RGB，也就是由Red（红色）、Green（绿色）、Blue（蓝色）三种颜色叠加能够获得人类所能感知的颜色。

在计算机中是用矩阵来表示图片的，如图所示。三个矩阵对应三个颜色通道，如果图片是64*64格式的，那么计算机表示这张图片是用三个矩阵来表示的，一般我们把三个二维64*64的矩阵合并成三维的矩阵，大小也就是64*64*3。通常用特征向量x来表示这个三维矩阵。而这个特征向量x的维度就是64*64*3=12288。

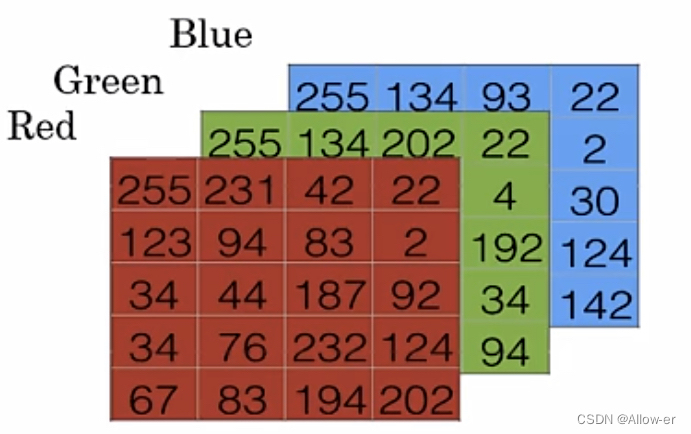
在二分类问题中，我们的目标是训练出一个分类器，将图片的特征向量x作为输入，预测输出的结果y是0还是1。

在机器学习中，我们用（x,y）来表示一个单独的样本，

其中x为n维特征向量，y为样本标签，，

训练集由m个训练样本构成，

能够用于解决二分类问题的机器学习算法有很多，例如线性回归，KNN，Logistic回归，SVM，决策树等等。

---

二、逻辑回归（Logistic回归）

在监督学习中，我们希望输入一个特征向量x，能够输出一个预测值 。

预测值  其实就是一个概率P(y=1 | x)，给出x值求其中y=1时的概率。

的取值介于0和1之间， 

例如上述猫图的例子，我们输入一个猫图，通过机器学习的算法或者神经网络，能够输出一个预测值1代表识别出它是猫。这个预测值  再与训练集中的标签 y 去对比，如果都是1或者0，代表这个机器预测正确。而评估这个机器学习算法的好坏程度的一个重要指标就是预测的准确率，在实际算实践中我们会给出大量的数据集进行训练来得到它的性能指标也就是预测准确率。

2.1 怎么通过计算输出概率呢？

首先会有两个参数(w和b)：w是一个n维向量，而b是一个实数。

后面讲到w和b的取值将会影响到成本函数（Cost Function）的大小。

2.1.1 线性回归模型

Output：     

线性回归就是用这个函数计算的，但是这不是一个好的二元分类算法，因为我们希望的取值介于0和1之间，而在线性模型中的值可能比1大得多，甚至是负值。

2.1.2 逻辑回归模型

逻辑回归模型就是将上述函数作用于sigmoid函数上

Output：

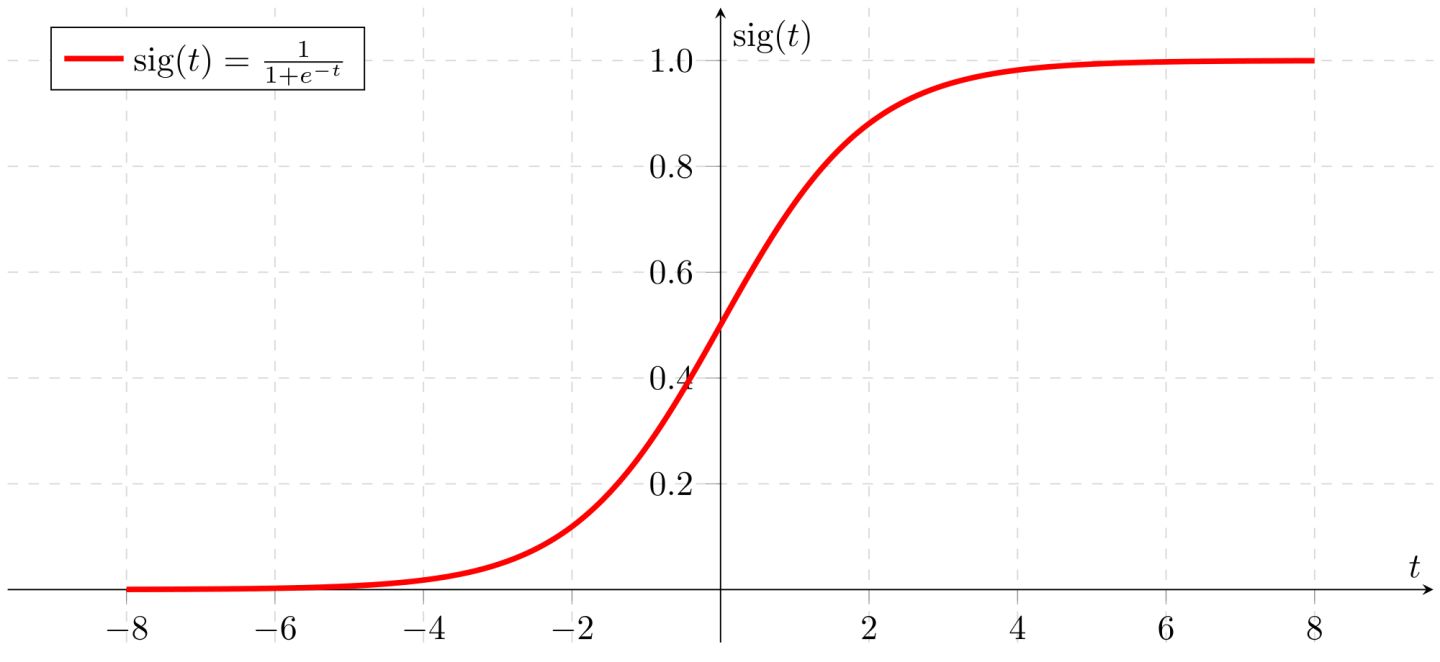
sigmoid函数的图形如下：

实际上这个函数取不到0和1，只能无限接近于0和1。这样就避免了线性模型的问题。取值都在0和1之间。

2.1.3总结：

这样我们就可以通过这个  函数计算输出的概率 。而学习参数w和b能够使变成较好的估计。

2.2 损失函数和成本函数

为了训练Logistic回归模型中的参数w和b，我们需要定义一个成本函数。

2.2.1 损失函数（Loss Function）

作用：用于衡量单一训练样例的效果。

如果我们将损失函数定义成这个样子：，来衡量预测输出值与实际值的接近程度。但是这样会发现到后面的优化问题时会出现非凸函数，使用梯度下降法的时候，会出现许多局部最优解，可能找不到全局最优解。

例如：非凸函数

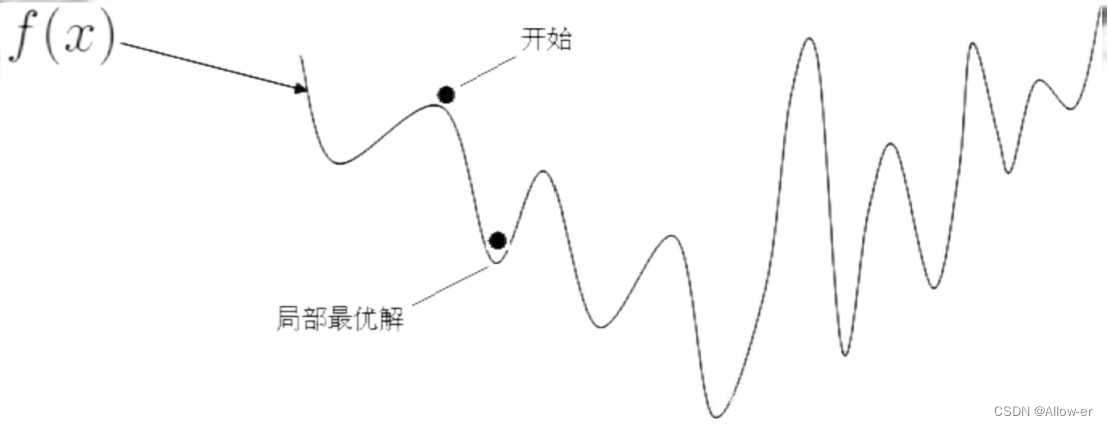
所以我们使用定义损失函数是这样子的：

Loss Function:  

 这个函数最后在优化问题时是一个凸函数，避免局部最优解的干扰。

例如：凸函数

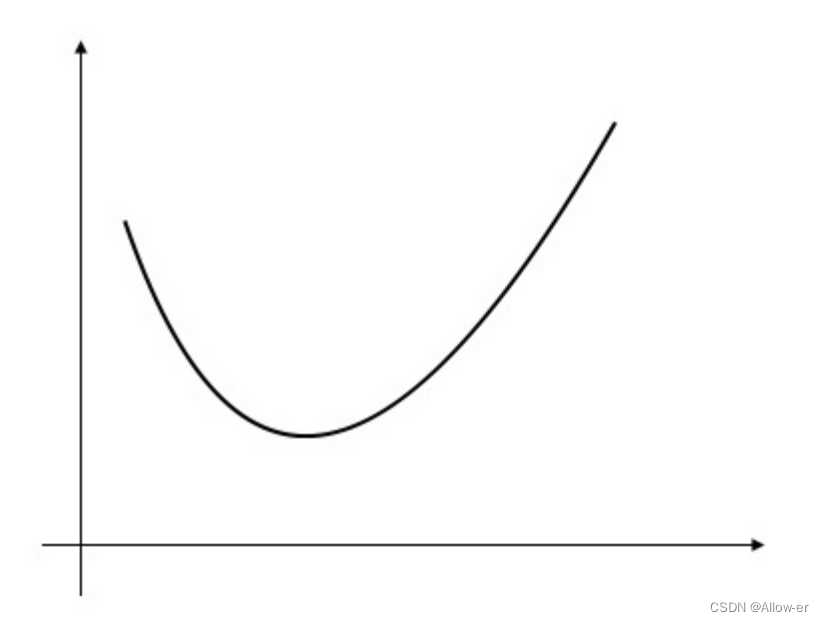
PS:为什么我们要凸函数而不是非凸的呢? 在后面的梯度下降法中你会明白的。现在你要做的就是记住这个凸函数的样子，然后耐心往下看.....

 2.2.2 成本函数（Cost Function）

作用：用于衡量全体训练样本上的表现。

Cost Function: 

(公式打出来不好看了......手写如下)

2.2.3 总结

我们希望能够使成本函数最小，所以我们需要找到参数w和b的值使得成本函数最小。接下来的梯度下降法就是用来寻找这样的参数w和b.

 2.3 梯度下降法

作用：来训练或者学习训练集上的参数w和b。

 如图所示：横轴表示参数w和b。为了简单w和b都看做实数，实际上w可能是更高维的。而成本函数（cost function）就是这个曲面，曲面的高度代表成本函数  在某一点的值。

而我们想要做的就是找到这个曲面的最低点对应的w和b的值使得成本函数J的值最小。

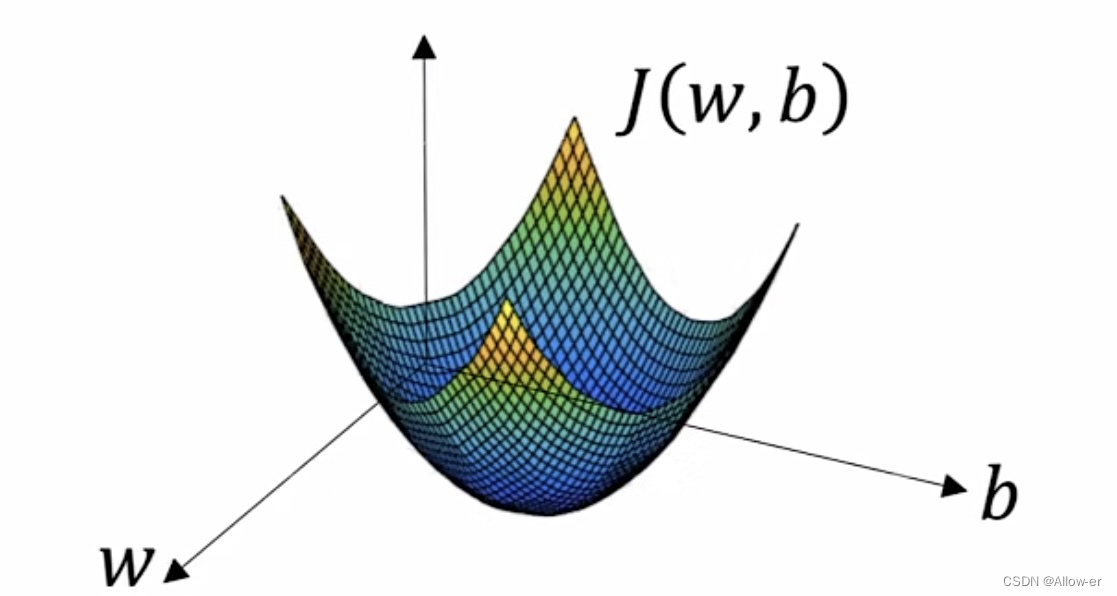
 看到这里就知道为什么我们在上面将损失函数定义成这个样子，这使得到这一步时的成本函数J的图像是一个凸函数，方便使用梯度下降法找到全局最优。相信到这里你会理解上面我们的操作了。

可能三维的看起来还是难以理解，那我们就把上面这个图像变成二维的，这样将会更加直观。我们以在w的维度来举例：

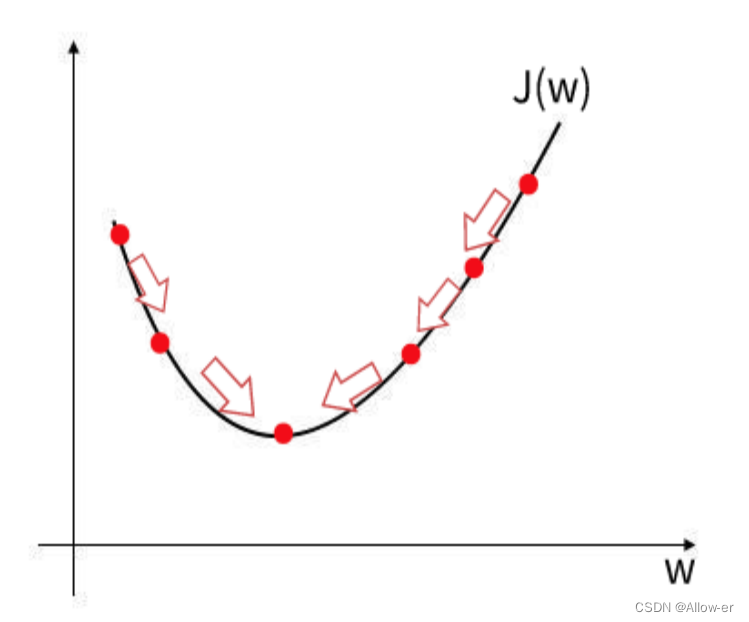
梯度下降法就是从初始点开始，向最陡峭的下坡方向走一步。找下降最快的地方。

例如你在一个山谷，你想用最快的速度到达谷底，肯定是想从下降最快的地方往下走，也就是坡度最陡的下坡处。

图中最低点就是w使得J(w)值最小的点，这样来看就很直观了，反之在b的维度也是如此，最后我们能够找到这样的w和b使得成本函数J的值最小。

接下来根据上面这个图我们引出w的更新表达式: 

其中：代表学习率，用于控制下降的步长，代表切线的斜率。

同理：b的更新表达式为：

三、手写笔记

可能文字太多会让人不想看，建议有时间的可以去看看视频学习会好很多，如果只想简单看看那我就把手写笔记放在这里了，我做的笔记可能有点潦草，但是我自己能够看懂，只作为参考，不喜勿喷，浅浅看看就好。

确实写这么一篇文章也要耗费大量时间，特别是公式啥的太难打了，如果你觉得这篇文章有用那就麻烦点点赞给个鼓励，也希望能够帮到你，可以收藏下来以备不时之需。