1、前言

• 我们在训练神经网络时，最常用到的方法就是梯度下降法。在了解梯度下降法前，我们需要了解什么是损失(代价)函数。所谓求的梯度，就是损失函数的梯度。
• 如果不知道什么是梯度下降的，可以看一下这篇文章：机器学习入门教学——梯度下降、梯度上升_恣睢s的博客-CSDN博客
• 损失函数其实就是神经网络里的标准和期望的标准相差多少的定量表达。（现有模型与期望模型的质量差距）
• 损失函数越小，现有模型就越逼近期望模型，现有模型的精度也就越高。
• 【注】损失函数和代价函数可以看作是两个概念不同的名字，但代表的函数和作用完全一样，通常可以互相替换使用，没有实质区别。
• 损失函数该如何设计呢？有三种方法：最小二乘法、极大似然估计法、交叉熵法。
  • 机器学习入门教学——损失函数（最小二乘法）
  • 机器学习入门教学——损失函数（极大似然估计法）
  • 机器学习入门教学——损失函数（交叉熵法）

 2、最小二乘法

• 比较现有模型与期望模型之间的差别，最简单的方法可能就是最小二乘法。
• 直接比较两个模型是不切实际的，可以通过对比它们的判断结果来实现。
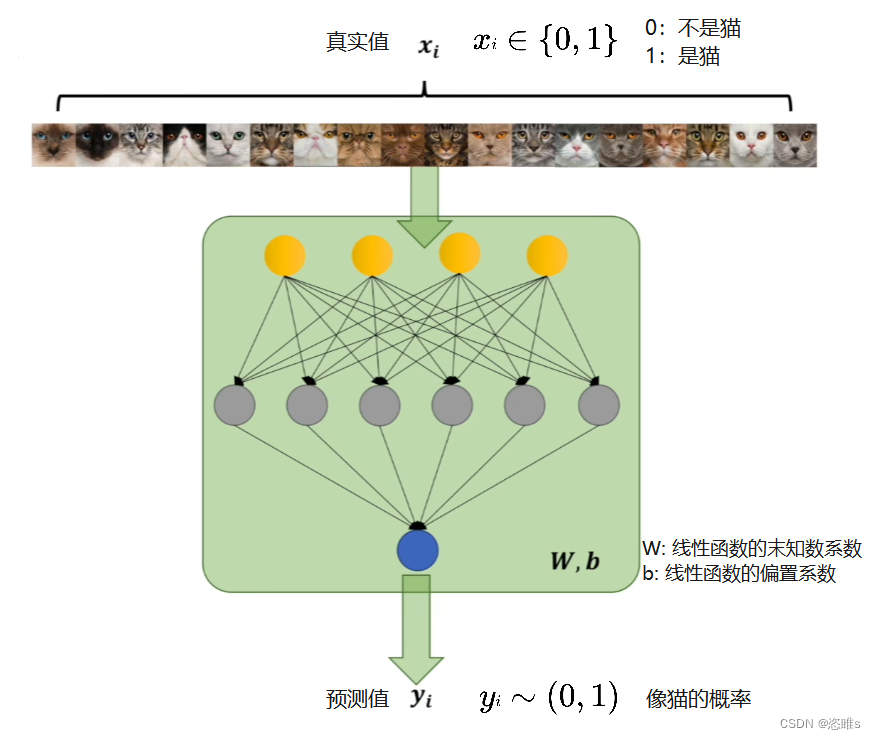
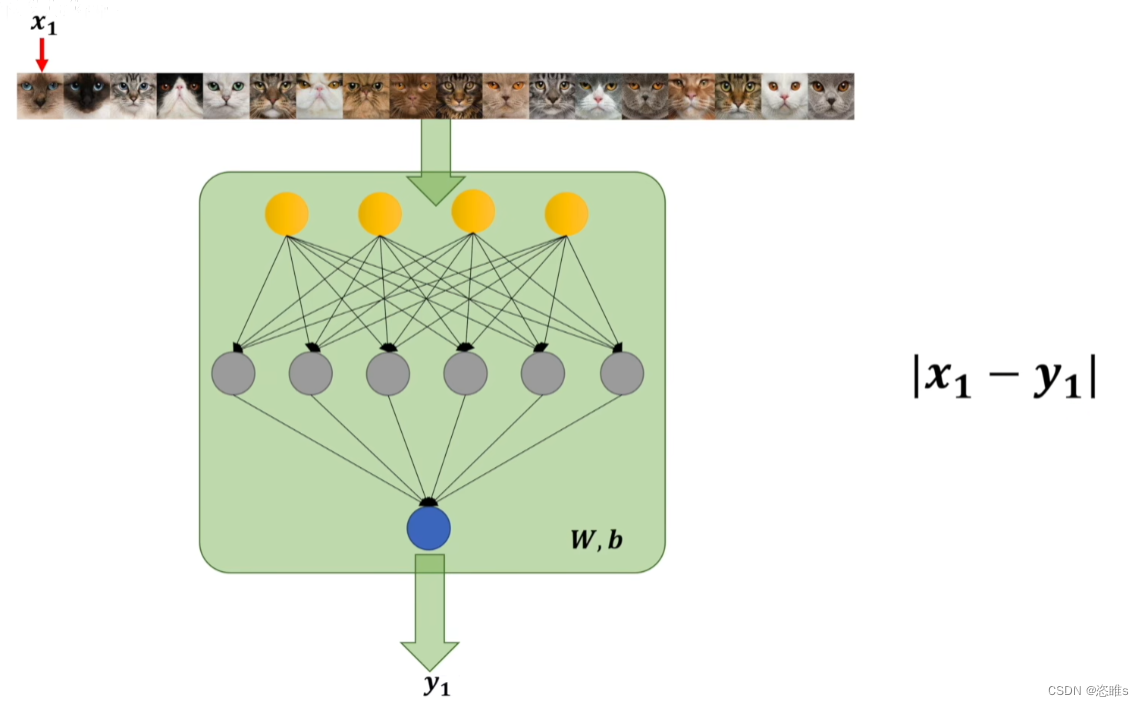
• 假设现有一个模型，用来判断一张图片是不是猫，根据判断结果来评估该模型与期望模型的差别。
  • 
• 其中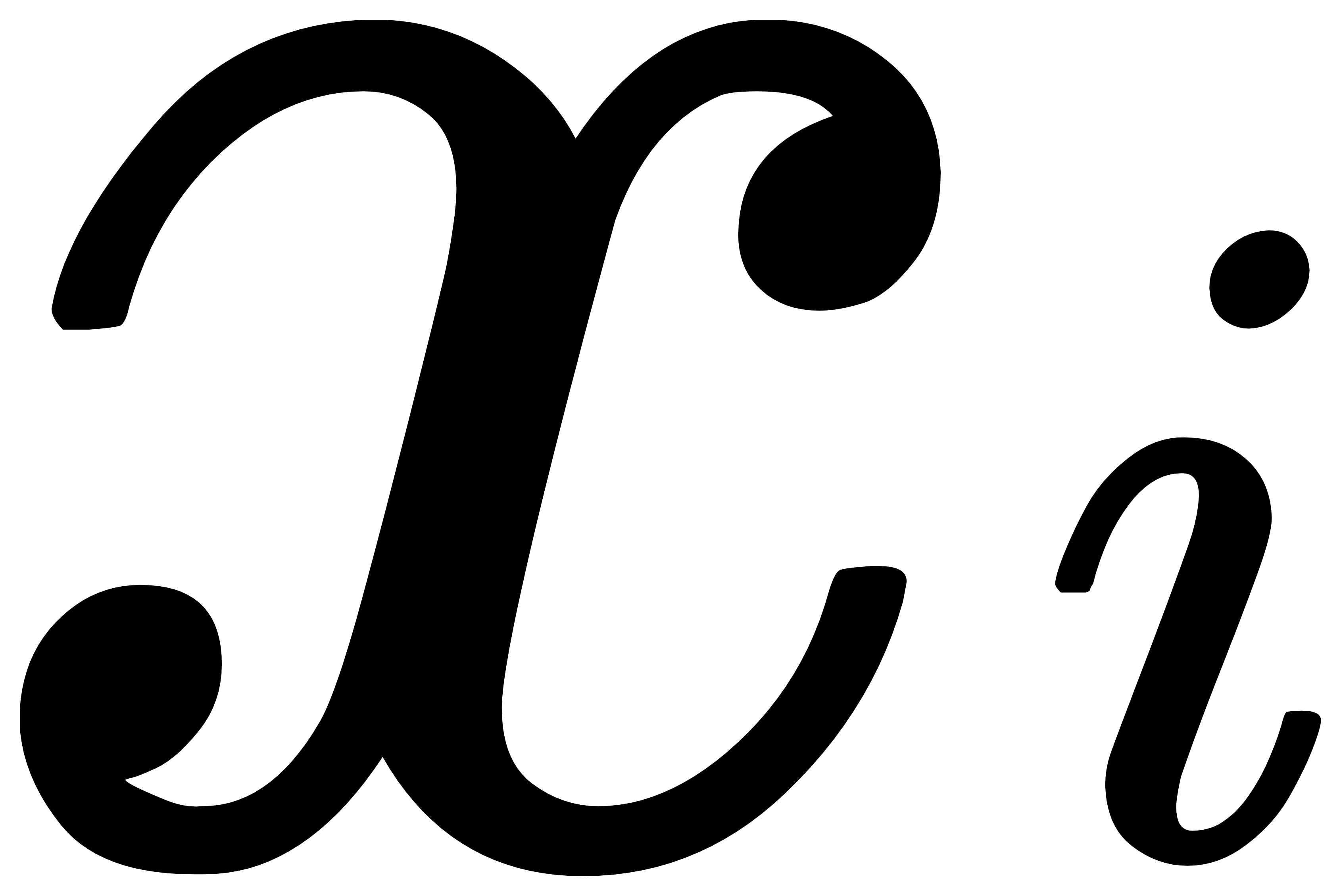，就表示期望模型的判断结果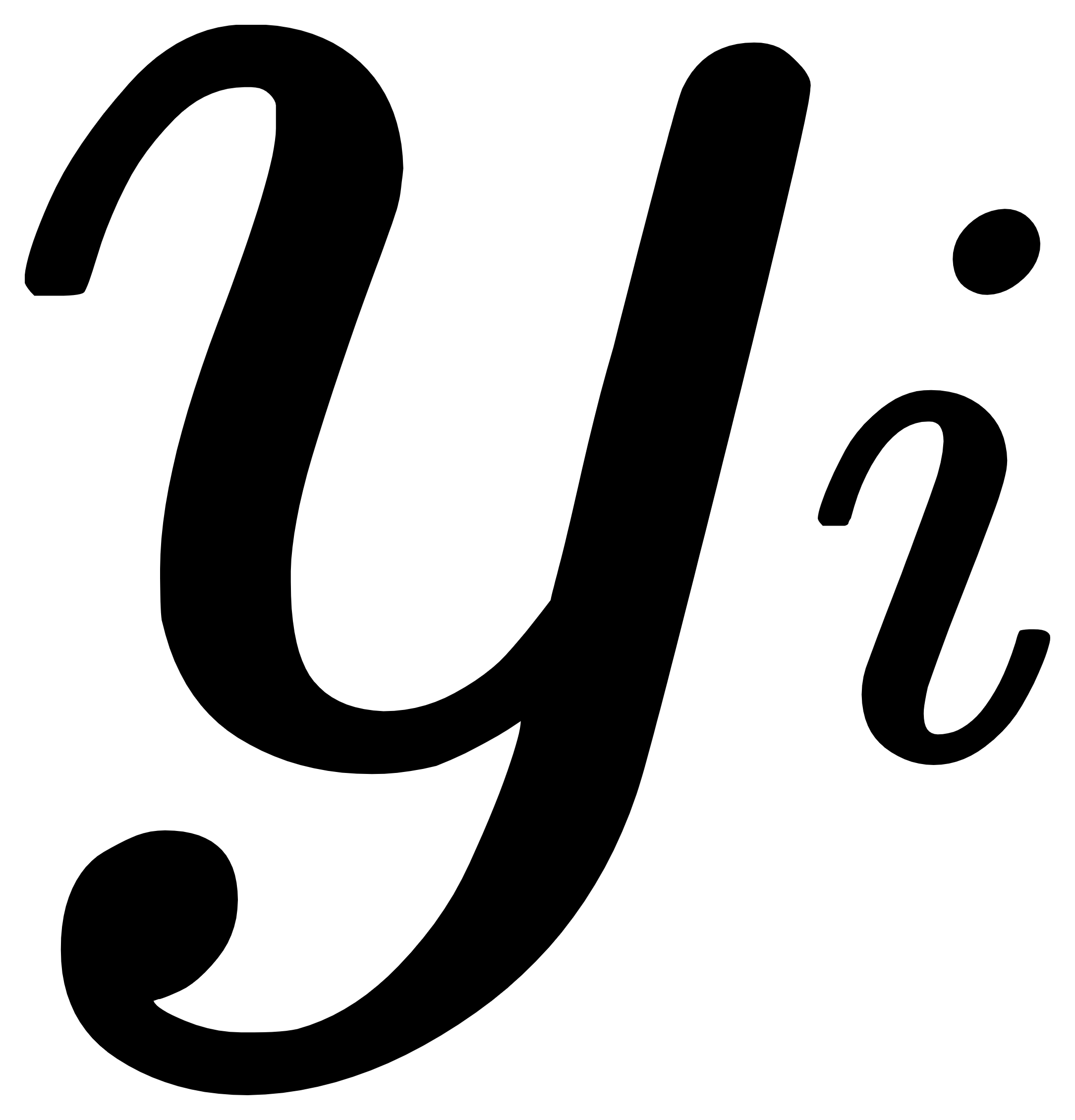，就表示现有模型的预测结果，即照片有多大的概率是猫。
• 先预测一张图片来表示它们之间的差距，即真实值减去预测值的绝对值。
  • 
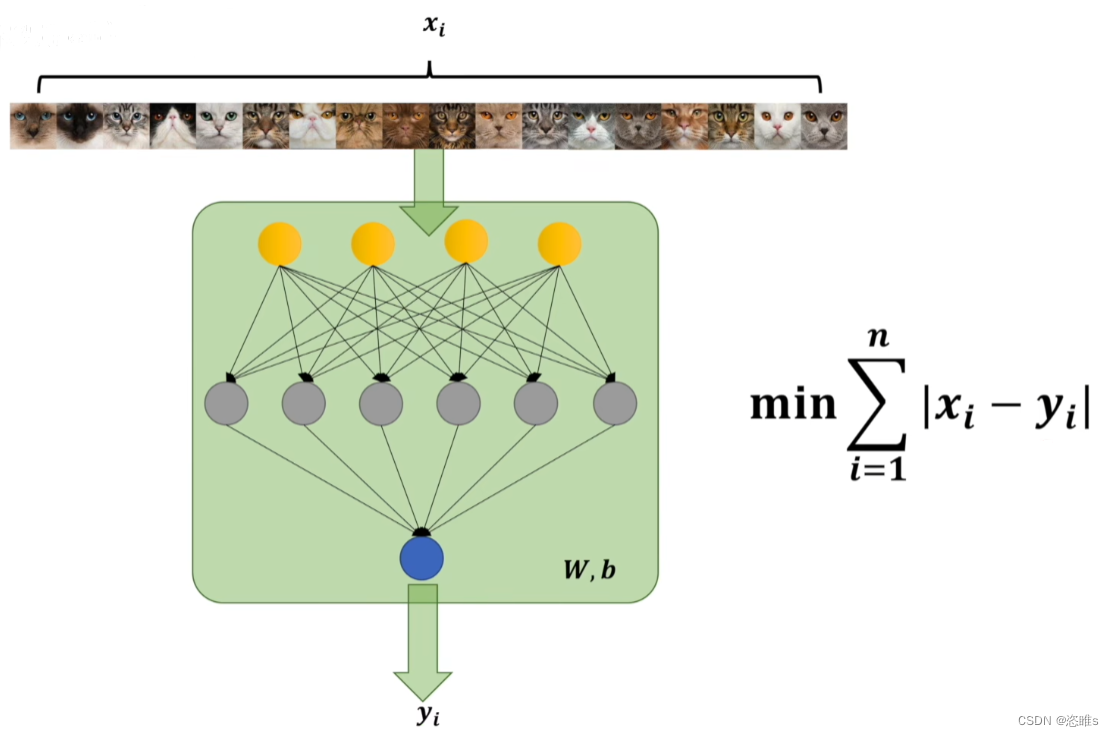
• 将所有图片的预测结果用来判断，并且取到最小值的时候，现有模型和预测模型之间的差距就是最小的，也就是精度是最高的。
  • 
• 但是，这个结果中有绝对值，我们知道绝对值在其定义域上不是全程可导的，所以我们可以改进一下。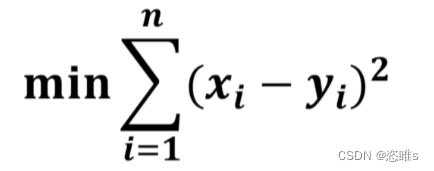，将其改成平方就能避免可导的问题，同时也能表达它们之间的差距。
• 这时我们就能理解为什么叫最小二乘法了，将真实值和预测值的差乘两次，并且取最小值。
• 【注】到这是不是发现最小二乘法和均方误差很像呢？其实有区别。最小二乘法作为损失函数时，没有除以总样本数m；而均方误差(MSE)作为损失函数时，除以了总样本数m。