前向传播和反向传播_BP神经网络分类问题正向传播和反向传播
BP神经网络可以用于解决回归问题也可以用于解决分类问题。本文将详细讲解BP网络用于解决分类问题的过程。其中包含了BP分类网络的基本结构和其正向传播和反向传播。1.分类问题的模型用于解决分类问题的BP网络通常像如下图中的结构:其中i是输入层,h是隐含层,o是输出层,s是softmax层。y是ground truth,即真实值。这里给网络中的参数赋予一些初始值,方便进行计算演示:2、正向传播首先看正向
BP神经网络可以用于解决回归问题也可以用于解决分类问题。
本文将详细讲解BP网络用于解决分类问题的过程。其中包含了BP分类网络的基本结构和其正向传播和反向传播。
1.分类问题的模型
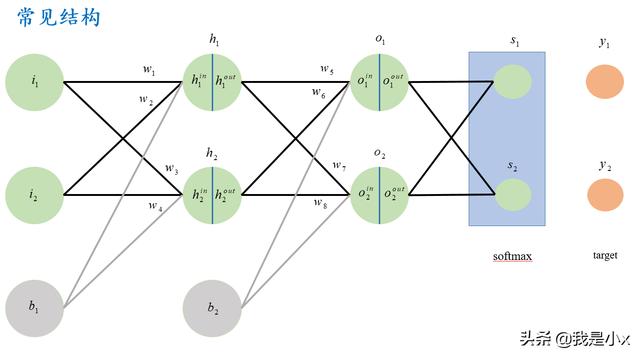
用于解决分类问题的BP网络通常像如下图中的结构:
其中i是输入层,h是隐含层,o是输出层,s是softmax层。y是ground truth,即真实值。
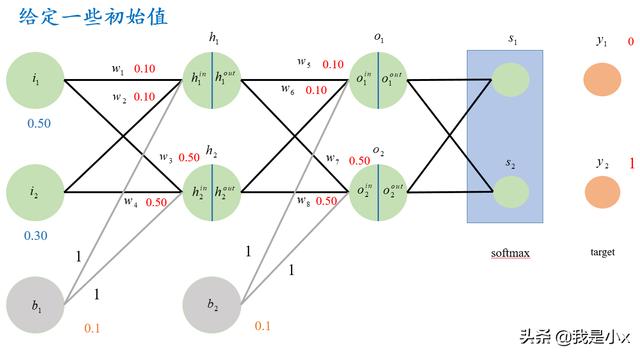
这里给网络中的参数赋予一些初始值,方便进行计算演示:
2、正向传播
首先看正向传播,首先看输入层向隐含层的传递。
隐含层的计算如下图所示。
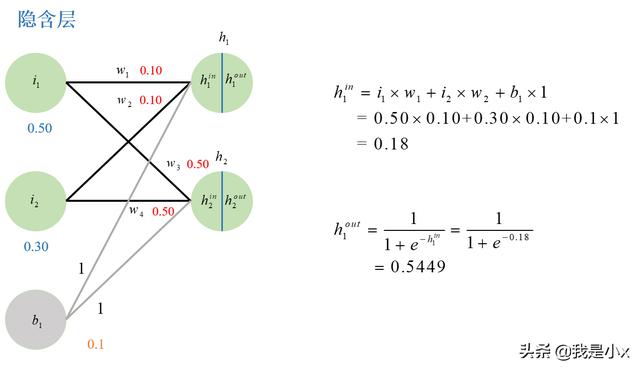
以隐含层h1计算
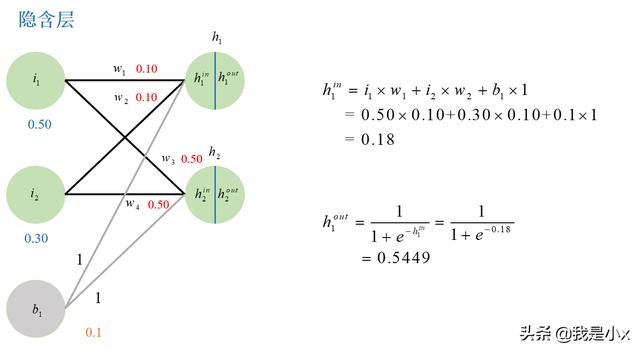
隐含层h2计算
接着看隐含层向输出层的传递。
输出层的计算如下图所示:
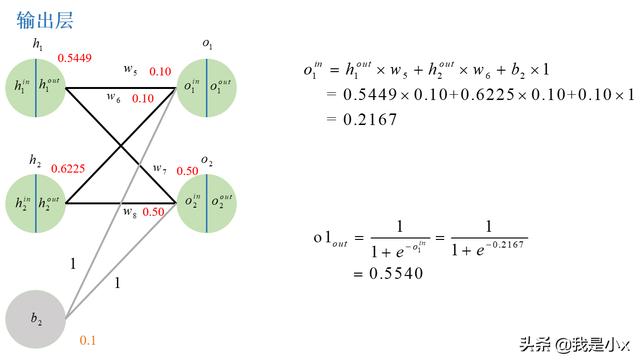
输出层o1计算
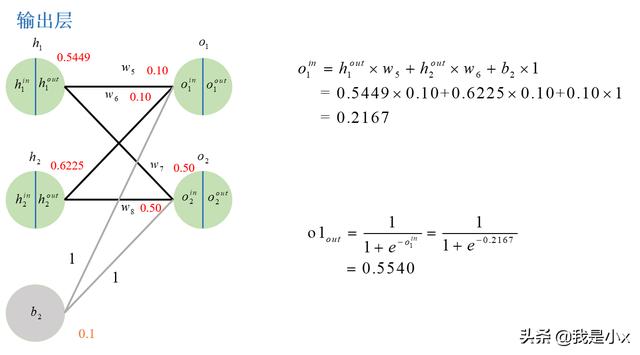
输出层o2计算
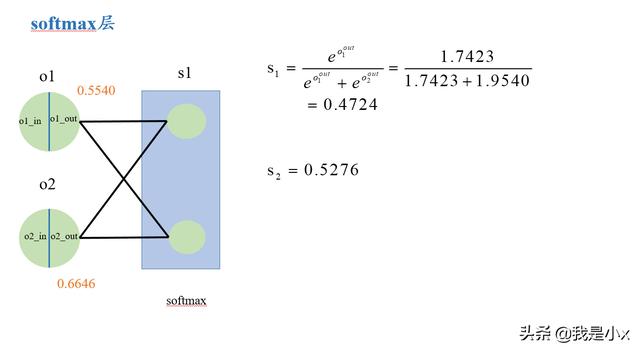
最后看输出层向softmax层的传递,
softmax的计算如下图所示
3.反向传播
反向传播中,分类问题与回归问题不同的是,增加了softmax层的反向传播。
那么问题来了,Softmax层如何求导?这是分类问题中的难点。
这里首先看一个通例,有m个输入元素z,然后通过softmax计算,形成了m个softmax元素s,s的计算公式如下图所示:
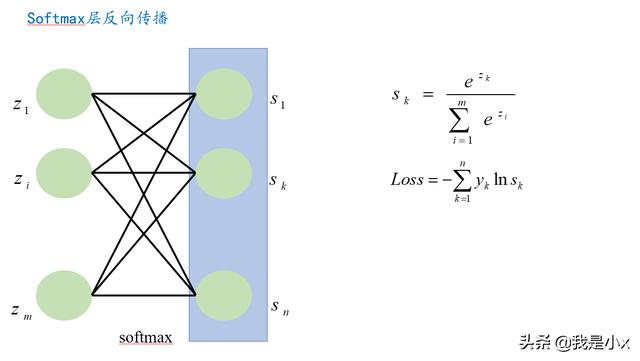
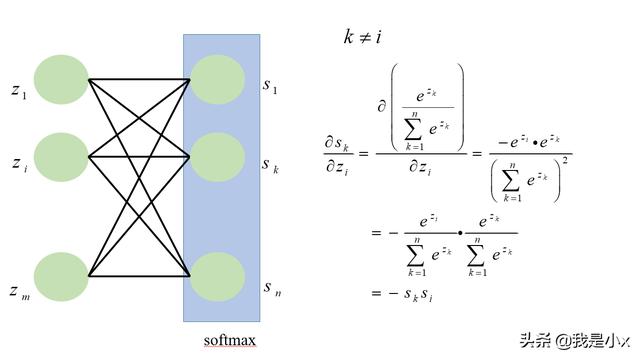
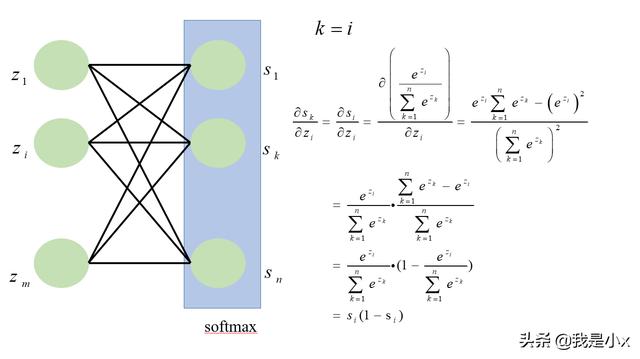

最后可以得到一个结论,即:

最后将这个公式带入到损失函数中,可以得到如下的结果:
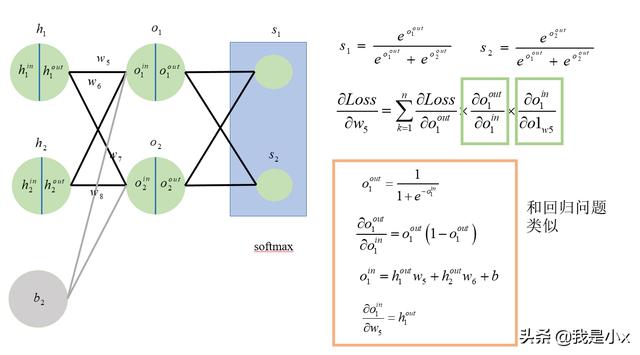
这样就可以得到Loss函数对w5的偏导数。
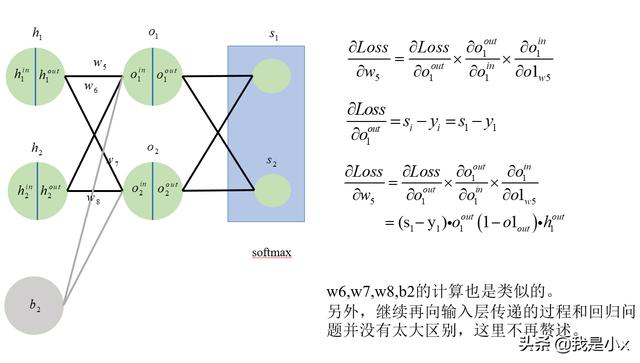
这里只推导了对Loss函数对w5的偏导数,实际上对w6,w7,w8的偏导数的计算是很类似的。这里不算赘述。
除此以外,对w1,w2,w3,w4的偏导数和回归问题并没有太大区别,这里不再赘述。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)