点击蓝字

关注本号

导读

五孔探针的数据处理方法可以用插值法，只要标定数据足够，插值法的精度就足够高。但在某些情况下，采用人工神经网络法的效果更好。比如需要外插的情况，或者标定数据存在局部误差偏大的情况等等。用插值法和人工神经网络法互相印证，可以提高结果的可信度。

说明

本方法来源于以前发表的一篇文章，感兴趣可参见：

“王洪伟，陈小龙，五孔探针的神经网络处理方法，航空动力学报，2010，25(2)，417-423”

这个程序用的是BP网络，本人对人工神经网络(ANN)的了解非常有限，只是利用Matlab现成的工具编写而已。

源代码分为两个：训练程序和计算程序。可以认为训练程序是拟合曲线的过程，而计算程序是用拟合好的曲线来计算的过程。当然ANN内部的关系式比曲线要复杂一些，但原理是类似的。

压力系数的定义和输入文件的格式与前面的文章“五孔探针的原理和数据处理方法”中插值法的完全相同，压力系数定义也相同，如下：

标定数据分为10列，分别为：马赫数，俯仰角，偏转角，总压，静压，p1, p2, p3, p4, p5。格式如下：

试验数据文件应该包含5列，对应p1-p5,单位为kPa，如下所示格式：

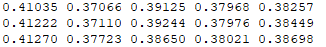
输出文件格式如下：

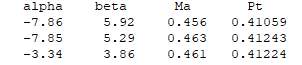
源代码

1. 训练程序的源代码如下：

%   人工神经网络(BP)

%   3个输入系数C_alpha,C_beta,C_ma，1个输出:alpha,beta,ma,C_pt之一

%   偏角系数：C_alpha=(p2-p3)/B

%   俯仰角系数：C_beta=(P4-P5)/B

%   Ma数系数：C_ma=(p2+p3+p4+p5)/4/p1

%   总压系数：C_pt=(pt-p1)/B

%   其中：B=p1-(p2+p3+p4+p5)/4

warning off MATLAB:divideByZero

clear all

%   载入数据

xydata=load('BH-5HB-002-Calib.dat');

%   无量纲化

range1=1:1183;

range2=1:1:1183;

ma=xydata(range1,1)';

beta=xydata(range1,2)'*pi/180;

alpha=xydata(range1,3)'*pi/180;

pt=xydata(range1,4)'/101.325;

p1=xydata(range1,6)'/101.325;

p2=xydata(range1,7)'/101.325;

p3=xydata(range1,8)'/101.325;

p4=xydata(range1,9)'/101.325;

p5=xydata(range1,10)'/101.325;

BB=p1-(p2+p3+p4+p5)/4;

C_alpha=(p2-p3)./BB;

C_beta=(p4-p5)./BB;

C_ma=(p1-BB)./p1;

C_pt=(pt-p1)./BB;

ma_t=xydata(range2,1)';

beta_t=xydata(range2,2)'*pi/180;

alpha_t=xydata(range2,3)'*pi/180;

pt_t=xydata(range2,4)'/101.325;

p1_t=xydata(range2,6)'/101.325;

p2_t=xydata(range2,7)'/101.325;

p3_t=xydata(range2,8)'/101.325;

p4_t=xydata(range2,9)'/101.325;

p5_t=xydata(range2,10)'/101.325;

BB_t=p1_t-(p2_t+p3_t+p4_t+p5_t)/4;

C_alpha_t=(p2_t-p3_t)./BB_t;

C_beta_t=(p4_t-p5_t)./BB_t;

C_ma_t=(p1_t-BB_t)./p1_t;

C_pt_t=(pt_t-p1_t)./BB_t;

%   建立网络

n1=10;

n2=10;

net=newff(minmax([C_alpha;C_beta;C_ma]),[n1 n2 1],{'tansig' 'tansig' 'purelin'},'trainlm');

net.trainParam.epochs=0.2e4;

net.trainParam.goal=1.e-8;

%   建立网络进行训练

net1=train(net,[C_alpha;C_beta;C_ma],alpha);

net2=train(net,[C_alpha;C_beta;C_ma],beta);

net3=train(net,[C_alpha;C_beta;C_ma],ma);

net4=train(net,[C_alpha;C_beta;C_ma],C_pt);

%   测试网络模拟情况

alphafit=sim(net1,[C_alpha_t;C_beta_t;C_ma_t]);

betafit=sim(net2,[C_alpha_t;C_beta_t;C_ma_t]);

mafit=sim(net3,[C_alpha_t;C_beta_t;C_ma_t]);

C_ptfit=sim(net4,[C_alpha_t;C_beta_t;C_ma_t]);

ptfit=C_ptfit.*BB_t+p1_t;

save('BH-5HB-002-Calib.mat','net1','net2','net3','net4')

%   画出仿真结果

figure(2);

subplot(2,2,1);

plot(range2,alpha_t*180/pi,'bo',range2,alphafit*180/pi,'rx');

title('Alpha');

subplot(2,2,2);

plot(range2,beta_t*180/pi,'bo',range2,betafit*180/pi,'rx');

title('Beta');

subplot(2,2,3);

plot(range2,ma_t,'bo',range2,mafit,'rx');

title('Ma');

subplot(2,2,4);

plot(range2,pt_t*101.325,'bo',range2,ptfit*101.325,'rx');

title('Pt');

训练过程需要几分钟到半小时，取决于标定数据点数和电脑的速度。下图是程序运行时的界面截图。分别点击“Performance”，“Training State”，和“Regression”可以查看训练过程中网络的优化过程，不过这都会大大降低训练速度。

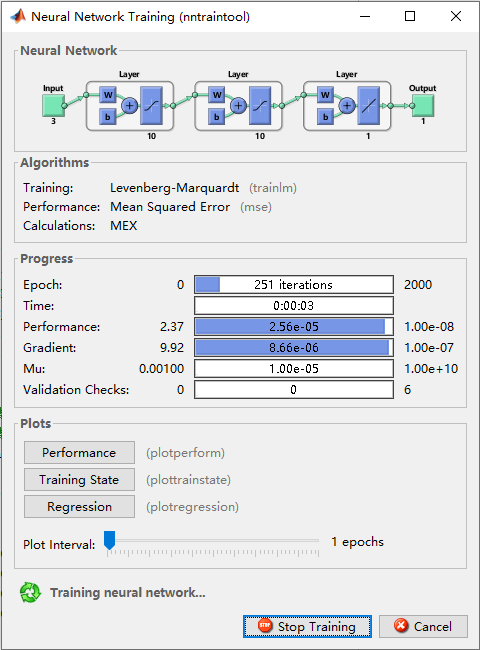
训练好的网络会被保存成*.mat格式，计算程序则要调用这个*.mat文件来进行计算。

2. 计算程序的源代码如下：

%   人工神经网络法

warning off MATLAB:divideByZero

clear all

load('BH-5HB-002-Calib.mat');     %   载入标定网络

xydata=load('P_test.dat');        %   载入试验数据

fid=fopen('Pout_ann.dat','w');    %   输出结果数据

p1_t=xydata(:,1)'/101.325*1000;

p2_t=xydata(:,2)'/101.325*1000;

p3_t=xydata(:,3)'/101.325*1000;

p4_t=xydata(:,4)'/101.325*1000;

p5_t=xydata(:,5)'/101.325*1000;

BB_t=p1_t-(p2_t+p3_t+p4_t+p5_t)/4;

C_alpha_t=(p2_t-p3_t)./BB_t;

C_beta_t=(p4_t-p5_t)./BB_t;

C_ma_t=(p1_t-BB_t)./p1_t;

alphafit=sim(net1,[C_alpha_t;C_beta_t;C_ma_t]);

betafit=sim(net2,[C_alpha_t;C_beta_t;C_ma_t]);

mafit=sim(net3,[C_alpha_t;C_beta_t;C_ma_t]);

C_ptfit=sim(net4,[C_alpha_t;C_beta_t;C_ma_t]);

ptfit=C_ptfit.*BB_t+p1_t;

alpha_out=alphafit*180/pi;

beta_out=betafit*180/pi;

ma_out=mafit;

pt_out=ptfit*101.325/1000;

fprintf(fid,'   alpha    beta      Ma       Pt\n');

fprintf('   alpha    beta      Ma       Pt\n');

for i=1:length(ma_out)

 fprintf(fid,'%8.2f %8.2f %8.3f %9.5f\n',alpha_out(i),beta_out(i),ma_out(i),pt_out(i));

end

fclose(fid);

完

我知道你  在看  哦