多项式回归

在线性回归中，我们通过如下函数来预测对应房屋面积的房价：

h θ ( x ) = θ 0 + θ 1 ∗ s i z e h_θ(x)=θ_0+θ_1∗size hθ​(x)=θ0​+θ1​∗size

通过程序我们也知道，该函数得到的是直线拟合，精度欠佳。现在，我们可以考虑对房价特征 s i z e size size 进行平方，以及获得更加精准的 s i z e size size 变化：

h θ ( x ) = θ 0 + θ 1 ∗ s i z e + θ 2 ∗ s i z e 2 hθ(x)=θ_0+θ_1∗size+θ_2∗size^2 hθ(x)=θ0​+θ1​∗size+θ2​∗size2

这就是多项式回归。

如下图所示，多项式回归得到了更好的拟合曲线。但我们也发现，在房屋面积足够大时，曲线反而出现了下沿，这意味着房价反而随着在房屋面积足够大时，与面积成反比，这明显不符合可观规律（虽然我们很渴望这样的情况出现）：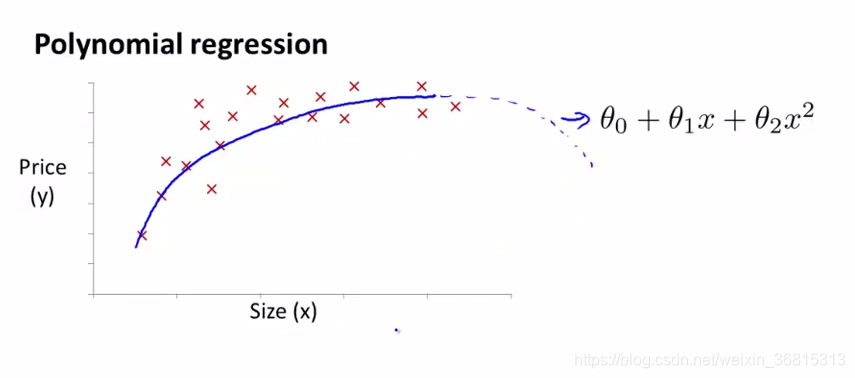
在这里插入图片描述
进一步地，我们考虑加上三次方项目或者替换二次方项为开方，得到如下两种预测：

( 1 ) h θ ( x ) = θ 0 + θ 1 ∗ s i z e + θ 2 ∗ s i z e 2 + θ 3 ∗ s i z e 3 (1)\quad h_θ(x)=θ_0+θ_1∗size+θ_2∗size^2+θ_3∗size^3 (1)hθ​(x)=θ0​+θ1​∗size+θ2​∗size2+θ3​∗size3
( 2 ) h θ ( x ) = θ 0 + θ 1 ∗ s i z e + θ 2 ∗ s i z e (2)\quad h_θ(x)=θ_0+θ_1∗size+θ_2∗\sqrt {size} (2)hθ​(x)=θ0​+θ1​∗size+θ2​∗size ​

在该例中，因为三次方项会带来很大的值，所以优先考虑采用了开方的预测函数。

# 机器学习 # 深度学习
Logo
技术共进，成长同行——讯飞AI开发者社区

技术共进，成长同行——讯飞AI开发者社区

更多推荐

机器学习与人工智能

python# 创建基类# 定义一对多关系# 定义多对一关系# 定义多对多关系（通过关联表）# 关联表（用于多对多关系）SQLAlchemy ORM提供了强大而灵活的数据库操作方式，通过本文的介绍，您应该能够：安装和配置SQLAlchemy定义数据模型和关系执行基本的CRUD操作构建复杂查询管理数据库事务遵循最佳实践SQLAlchemy还有更多高级特性，如混合属性、事件监听、自定义查询等，值得进一

avatar 讯飞AI开发者社区

AI革新药物研发：基因组大数据新突破

基因组大数据分析已成为药物研发的核心环节，人工智能（AI）技术通过高效处理海量数据，显著加速了靶点发现、药物筛选和个性化治疗等流程。来源网站：pyklqwq.cn/article/25jNXMc/39830.html。来源网站：pyklqwq.cn/article/25KljJd/61632.html。来源网站：pyklqwq.cn/article/25AECkl/15960.html。来源网站：

avatar 讯飞AI开发者社区

多模态上下文工程化落地：提示工程架构师的ROI提升策略

在当今数字化浪潮中，人工智能技术日新月异。多模态数据，即包含文本、图像、音频、视频等多种形式的数据，正变得无处不在。想象一下，我们生活在一个信息丰富多样的世界里，就如同走进了一个大型的多媒体图书馆，每本书可能是文本形式，墙上挂着画作（图像），角落里播放着音乐（音频），还有视频在循环展示各种内容。多模态数据就像这个图书馆里丰富多样的信息载体。对于提示工程架构师而言，如何有效地处理和利用多模态上下文信

avatar 讯飞AI开发者社区