生成对抗网络系列

Generative Adversarial Networks（GAN）

Paper : Generative Adversarial Networks

生成对抗网络

Discriminator Network

判别网络

• 判别网络$D(\mathbf{x};\varphi )$的目标是区分出一个样本是否来自于真实分布还是来自于生成网络生成的数据，所以判别网络是一个二分类器

• 给定一个样本$(x,y),y=1,0$表示其来自于真实样本或生成样本，判别网络的损失函数为交叉熵

  $$\underset{\varphi }{\min }-\left({\mathbb{E}}_x[y\log p(y=1\mid \mathbf{x})+(1-y)\log p(y=0\mid \mathbf{x})]\right)$$

  • 若训练中判别网络输入的样本数据由真实样本和生成样本各参半混合而成，则损失函数等价于

  $$\begin{array}{rl}& \underset{\varphi }{\max }{\mathbb{E}}_{x\sim p_r(x)}[\log D(\mathbf{x};\varphi )]+{\mathbb{E}}_{{\mathbf{x}}^{\prime }\sim p_{\theta }\left(x^{\prime }\right)}\left[\log \left(1-D\left({\mathbf{x}}^{\prime };\varphi \right)\right)\right]\\ =& \underset{\varphi }{\max }{\mathbb{E}}_{\mathbf{x}\sim p_r(x)}[\log D(\mathbf{x};\varphi )]+{\mathbb{E}}_{\mathbf{z}\sim p(z)}[\log (1-D(G(\mathbf{z};\theta );\varphi ))]\end{array}$$
  其中$\theta$和$\varphi$分别是生成网络和判别网络的参数

Generator Network

生成网络

• 生成网络的目标是生成让判别网络判别为真实样本的生成样本，损失函数为

  $$\begin{array}{rl}& \underset{\theta }{\max }\left({\mathbb{E}}_{z\sim p(z)}[\log D(G(\mathbf{z};\theta );\varphi )]\right)\\ =& \underset{\theta }{\min }\left({\mathbb{E}}_{z\sim p(z)}[\log (1-D(G(\mathbf{z};\theta );\varphi ))]\right)\end{array}$$

  $$\underset{\theta }{\min }\left({\mathbb{E}}_{z\sim p(z)}[-\log D(G(\mathbf{z};\theta );\varphi )]\right)$$

  • 上述两个目标函数其实是等价的，但实际一般选择前者，因为其梯度性质更好。$log$函数在x接近于1时的梯度要比接近0时的梯度小很多。当判别网络$D$以很高的概率认为生成网络$G$产生的样本是“假”样本（往往发生在训练初期），即$(1-D(G(z;\theta );\varphi ))\to 1$，这时目标函数关于$\theta$的梯度相对很小，从而不利于优化。

  • 可以将$D(G(\mathbf{z};\theta );\varphi )$与$(1-D(G(\mathbf{z};\theta );\varphi ))$分别看成一个整体$y$，从而损失函数对模型参数$\theta$的导数可以看成先对$\log y$求导，再乘上$y$对$\theta$求导。而$y$对$\theta$求导的结果绝对值是一样的，正好对应max和min。损失函数对$y$的导数在使用后者作为损失函数时，且当$(1-D(G(z;\theta );\varphi ))\to 1$时，梯度接近于$log$函数$x=1$处的导数值，较小，优化力度小

  • 这种梯度优化手段还可通过交换真实与生成样本的标签来实现，即真实样本标签改为$0$，生成样本标签改为$1$

训练

• GAN的训练比较难，往往不太稳定，因为两个网络的优化目标刚好相反。一般情况下，需要平衡两个网络的能力。对于判别网络来说，一开始的判别能力不能太强，否则难以提升生成网络的能力。但是，判别网络的判别能力也不能太弱，否则针对它训练的生成网络也不会太好。在训练时需要使用一些技巧，使得在每次迭代中，判别网络比生成网络的能力强一些，但又不能强太多。

• 训练流程如下所示：每次迭代时，判别网络更新K次（超参数），而生成网络更新一次，即首先要保证判别网络足够强才能开始训练生成网络。

  

Deep Convolutional Generative Adversarial Network（DCGAN）

Paper : Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks

深度卷积生成对抗网络

• 判别网络为一个简单的DNN

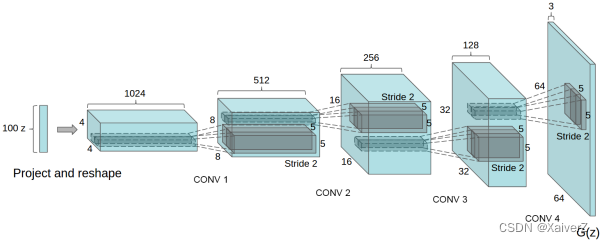
• 生成网络使用微步卷积来实现。最开始的输入为从均匀分布中随机采样的100维向量$z$，通过全连接层将其映射到$4\times 4\times 1024$的维度上

  

GAN Training Problem

知乎

Paper : TOWARDS PRINCIPLED METHODS FOR TRAINING GENERATIVE ADVERSARIAL NETWORKS

本部分分析GAN的训练问题

Training Stability

训练稳定性

• GAN的判别器$D$的目标函数为最大化如下式子，即尽可能将真实样本分成正例，将生成样本分成负例

  max ⁡ { E x ∼ P r [ log ⁡ D ( x ) ] + E x ∼ P g [ log ⁡ ( 1 − D ( x ) ) ] } \max{\{\mathbb{E}_{x \sim \mathbb{P}_{r}}[\log D(x)]+\mathbb{E}_{x \sim \mathbb{P}_{g}}[\log (1-D(x))]\}} max{Ex∼Pr​​[logD(x)]+Ex∼Pg​​[log(1−D(x))]}
  其中$P_r$为真实样本分布，$P_g$为生成器产生的样本分布

• GAN的生成器$G$的目标函数为最小化如下式子，即尽生成样本能尽可能欺骗过判别器，使其判断为真实样本

  min ⁡ { E x ∼ P g [ log ⁡ ( 1 − D ( x ) ) ] } \min{\{\mathbb{E}_{x \sim P_{g}}[\log (1-D(x))]\}} min{Ex∼Pg​​[log(1−D(x))]}

• 从判别器$D$的损失函数我们可以推出，当$P_r$与$P_g$固定时，即生成器参数不变时，最优的判别器$D$应该是怎样的，判别器的损失函数可以等价为最大化如下式子

  m a x { P r ( x ) log ⁡ [ D ( x ) ] + P g ( x ) log ⁡ [ 1 − D ( x ) ] } max{\{P_{r}(x) \log [D(x)]+P_{g}(x) \log [1-D(x)]\}} max{Pr​(x)log[D(x)]+Pg​(x)log[1−D(x)]}

  • 令上式关于$D(x)$的导数为零

  $$\frac{P_r(x)}{D(x)}-\frac{P_g(x)}{1-D(x)}=0$$
  得到最优判别器

  $$D^{\ast }(x)=\frac{P_r(x)}{P_r(x)+P_g(x)}$$
  其中，判别器$D(x)$输入样本$x$，输出该样本来自真实分布的概率

  • 给生成器的目标函数加上一个与生成器无关的项

  min ⁡ { E x ∼ P r [ log ⁡ D ( x ) ] + E x ∼ P g [ log ⁡ ( 1 − D ( x ) ) ] } \min{\{\mathbb{E}_{x \sim P_{r}}[\log D(x)]+\mathbb{E}_{x \sim P_{g}}[\log (1-D(x))]\}} min{Ex∼Pr​​[logD(x)]+Ex∼Pg​​[log(1−D(x))]}
  最小化上式等价于最小化生成器的目标函数

  • 为了探究当判别器$D$最优时，会对生成器$G$的训练有什么影响，将$D^{\ast }(x)$代入上式

  min ⁡ { E x ∼ P r log ⁡ P r ( x ) 1 2 [ P r ( x ) + P g ( x ) ] + E x ∼ P g log ⁡ P g ( x ) 1 2 [ P r ( x ) + P g ( x ) ] − 2 log ⁡ 2 } = min ⁡ { 2 J S ( P r ∥ P g ) − 2 log ⁡ 2 } \min{\{\mathbb{E}_{x \sim P_{r}} \log \frac{P_{r}(x)}{\frac{1}{2}\left[P_{r}(x)+P_{g}(x)\right]}+\mathbb{E}_{x \sim P_{g}} \log \frac{P_{g}(x)}{\frac{1}{2}\left[P_{r}(x)+P_{g}(x)\right]}-2 \log 2\}} = \min{\{2 J S\left(P_{r} \| P_{g}\right)-2 \log 2\}} min{Ex∼Pr​​log21​[Pr​(x)+Pg​(x)]Pr​(x)​+Ex∼Pg​​log21​[Pr​(x)+Pg​(x)]Pg​(x)​−2log2}=min{2JS(Pr​∥Pg​)−2log2}
  所以，当判别器$D$越接近最优，生成器$G$的目标函数就越等价于最小化$P_r$与$P_g$的JS散度。当两个分布越接近时，JS散度的值越小；当两个分布完全相同时，其JS散度为0。但JS散度存在一个问题，当两个分布完全不相关不重叠（或有部分可忽略的小范围重叠）时，JS散度的值为一个常数。

  • 由$KL\left(P_1\Vert P_2\right)={\mathbb{E}}_{x\sim P_1}\log \frac{P_1}{P_2}$与$JS\left(P_1\Vert P_2\right)=\frac{1}{2}KL\left(P_1\Vert \frac{P_1+P_2}{2}\right)+\frac{1}{2}KL\left(P_2\Vert \frac{P_1+P_2}{2}\right)$可知，当两个分布$P_1$，$P_2$无重叠或重叠部分可忽略时，有如下四种情况

    • $P_1(x)=0,P_2(x)=0$

    • $P_1(x)\ne 0,P_2(x)\ne 0$

    • $P_1(x)=0,P_2(x)\ne 0$

    • $P_1(x)\ne 0,P_2(x)=0$

  • 第一种情况下JS散度为$0$；第二种情况由于重叠可忽略所以JS散度也为$0$；第三种情况JS散度为$\log 2$；第四种情况类似JS散度为$\log 2$

  • 因此，在近似最优判别器条件下，最小化生成器的目标函数等价于最小化$P_r$与$P_g$之间的JS散度，而由于$P_r$与$P_g$几乎不可能有不可忽略重叠（特别是在训练刚开始时）（详见知乎解释），所以无论它们相距多远JS散度都是常数$\log 2$，最终导致生成器的梯度接近于0，生成器梯度消失

• 综上，GAN训练不稳定的原因如下

  • 判别器训练地太好，生成器梯度消失，Loss降不下去

  • 判别器训练得不好，生成器梯度不准

  • 只有当判别器训练地不好不坏才行，但这个程度很难把握，因此GAN很难训练

Model Collapse

模型坍塌

• 生成器$G$的目标函数可以等价地写成

  min ⁡ { E x ∼ P g [ − log ⁡ D ( x ) ] } \min{\{\mathbb{E}_{x \sim P_{g}}[-\log D(x)]\}} min{Ex∼Pg​​[−logD(x)]}
  将最优判别器$D^{\ast }(x)$代入上式

  $$\begin{array}{rl}{\mathbb{E}}_{x\sim P_g}\left[-\log D^{\ast }(x)\right]& =KL\left(P_g\Vert P_r\right)-{\mathbb{E}}_{x\sim P_g}\log \left[1-D^{\ast }(x)\right]\\ & =KL\left(P_g\Vert P_r\right)-2JS\left(P_r\Vert P_g\right)+2\log 2+{\mathbb{E}}_{x\sim P_r}\left[\log D^{\ast }(x)\right]\end{array}$$
  注意到最后两项不依赖于生成器$G$，所以最小化上式等价于最小化

  min ⁡ { K L ( P g ∥ P r ) − 2 J S ( P r ∥ P g ) } \min{\{K L\left(P_{g} \| P_{r}\right)-2 J S\left(P_{r} \| P_{g}\right)\}} min{KL(Pg​∥Pr​)−2JS(Pr​∥Pg​)}

  • 最小化上式等价于最小化$P_r$与$P_g$之间的KL散度，同时又要最大化两者的JS散度，直观上就非常的不靠谱。JS散度的问题前述已经讨论过，下面讨论KL散度的问题。

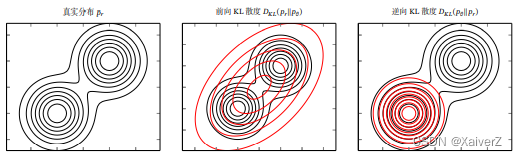
  • 由于KL散度是一种非对称的散度，在计算$P_r$与$P_g$之间的KL散度时，按照顺序的不同，存在两种KL散度：（假设真实分布$P_r$为混合高斯分布，生成器样本分布$P_g$为高斯分布）

    • 前向KL散度

      Forward KL Divergence

      $$\mathrm{KL}\left(P_r,P_g\right)=\int P_r(\mathbf{x})\log \frac{P_r(\mathbf{x})}{P_g(\mathbf{x})}\mathrm{d}\mathbf{x}$$

      • 当$P_r(x)\to 0$，$P_g(x)>0$时，KL散度为$0$

      • 当$P_r(x)>0$，$P_g(x)\to 0$时，KL散度趋于无穷大

      • 在前向KL散度中，第二种情况会使$P_g$会倾向于生成更多多样性样本，覆盖$P_r$的整个分布区域；第一种情况会使$P_g$覆盖$P_r$分布之外的邻近区域，因为这不会造成KL散度增大

    • 逆向KL散度

      Reverse KL Divergence

      $$\mathrm{KL}\left(P_g,P_r\right)=\int P_g(\mathbf{x})\log \frac{P_g(\mathbf{x})}{P_r(\mathbf{x})}\mathrm{d}\mathbf{x}$$

      • 当$P_r(x)\to 0$，$P_g(x)>0$时，KL散度趋于无穷大

      • 当$P_r(x)>0$，$P_g(x)\to 0$时，KL散度为$0$

      • 在逆向KL散度中，第一种情况使$P_g$会倾向于生成更“安全”的样本，避免覆盖到$P_r$无分布或分布中较稀疏的区域；第二种情况使$p_g$对$P_r$的分布区域不敏感，就算$P_r$有分布的区域，若$P_g$无分布，KL散度也不会增大。

  • 由前述分析可知，在最优判别器条件下，生成器实际上最小化的是分布$P_r$与$P_g$的逆向KL散度，因此会使生成器倾向于生成一些更“安全”的样本，减少了样本多样性，产生模型坍塌（Model Collapse）

Wasserstein GAN

知乎

Paper : Wasserstein GAN

WGAN

• WGAN是一种使用（1st）Wasserstein距离来代替JS散度优化GAN的训练过程

  $$W\left(P_r,P_g\right)=\underset{\gamma \sim \Pi \left(P_r,P_g\right)}{\inf }{\mathbb{E}}_{(x,y)\sim \gamma }[\Vert x-y\Vert ]$$
  其中$\Pi \left(P_r,P_g\right)$是所有可能的联合分布的集合

  • 两个分布$P_r$和$P_g$的Wasserstein距离往往难以计算，作者用了一个已有定理将其等价替换为如下形式

  $$W\left(P_r,P_g\right)=\frac{1}{K}\underset{\Vert f{\Vert }_L\le K}{\sup }{\mathbb{E}}_{x\sim P_r}[f(x)]-{\mathbb{E}}_{x\sim P_g}[f(x)]$$
  其中$\Vert f{\Vert }_L\le K$表示函数$f$的Lipschitz常数$\Vert f{\Vert }_L$要小于$K$

• 评价网络

  Critic Network

  • 我们可以用一组参数$w$来定义一系列可能的函数$f_w$，求解上式可近似为求解

  $$K\cdot W\left(P_r,P_g\right)\approx \underset{w:{|f_w|}_L\le K}{\max }{\mathbb{E}}_{x\sim P_r}\left[f_w(x)\right]-{\mathbb{E}}_{x\sim P_g}\left[f_w(x)\right]$$
  其中$f_w$称为评价网络（Critic Network），代替了判别网络。和标准GAN中判别网络有所不同，判别网络是做分类任务，而评价网络是回归任务，即对于真实样本，打分尽可能高；对于生成样本，打分尽可能低。所以评价网络无需sigmoid函数。

  • 另外，由于$\Vert f{\Vert }_L\le K$的限制，作者直接限制$f_w$的所有参数值域不超过某个范围$[-c,c]$（$c$为一个比较小的正数，例如0.01）。由于偏导数的大小一般和参数取值有关，所以将参数限制在某个范围，其实也能达到使其梯度限制在某个范围。

  • 综上，评价网络的损失函数为

    个人理解：评价网络的损失函数含义并不是最小化真实分布与生成分布之间的Wasserstein距离（虽然是它的形式），但在本文$f_w$判别网络的设定下，使其表面上的含义恰好与评价网络的优化目标吻合，即真实样本打分尽量高，生成样本打分尽量低

  $${\mathbb{E}}_{x\sim P_g}\left[f_w(x)\right]-{\mathbb{E}}_{x\sim P_r}\left[f_w(x)\right]$$

• 生成网络

  Generator Network

  $$K\cdot W\left(P_r,P_g\right)\approx \underset{w:{|f_w|}_L\le K}{\max }{\mathbb{E}}_{x\sim P_r}\left[f_w(x)\right]-{\mathbb{E}}_{x\sim P_g}\left[f_w(x)\right]$$

  • 上式衡量了Wasserstein距离，所以生成器的损失函数可以是最小化上式，但由于第一项与生成器无关，所以生成器的损失函数为

  $$-{\mathbb{E}}_{x\sim P_g}\left[f_w(x)\right]$$

• 综上所示，WGAN相对于GAN其实就改了四点

  • 判别器取消最后一层的sigmoid

  • 生成器和判别器的Loss不取Log（即不使用交叉熵，直接将神经网络的输出Logit当Loss用；为什么这么做都是基于前述理论推导出来的，推导很复杂，但改动的地方很简单）

  • 每次更新判别器的参数之后，都将它们的值截断到不超过一个固定常数$c$（因为在推导过程中将$f$参数化为$f_w$，作为判别器或评价网络，必须满足Lipschitz的条件，而生成器与$f_w$无关，不需要截断）

  • 不要用基于动量的优化算法（如Adam和Momentum），推荐RMSProp，SGD也可