ResNet:深度神经网络的突破与应用解析
本文聚焦于ResNet深度神经网络,介绍其由Microsoft研究团队于2015年提出,在ImageNet和COCO数据集比赛中表现卓越。剖析了ResNet的特点、优点,阐述了其网络结构,深入分析了更深网络层数面临的问题及ResNet的创新解决方法,如残差结构和Batch Normalization。指出了ResNet存在的不足,并提供了代码实现示例,旨在为读者全面了解ResNet提供参考。
前言
在计算机视觉领域,深度神经网络的发展日新月异,不断推动着图像识别、目标检测等任务的进步。然而,随着网络层数的增加,传统神经网络面临着诸多挑战,如梯度消失、梯度爆炸以及网络退化等问题,严重限制了网络性能的提升。ResNet(残差网络)的出现犹如一场及时雨,为解决这些难题带来了新的思路和方法。本文将深入剖析ResNet的基本原理、网络结构、创新之处、存在的问题以及代码实现,带您全面了解这一具有里程碑意义的深度神经网络。
ResNet
一、网络的基本介绍
ResNet(“残差网络”的简称)是由Microsoft研究团队于2015年提出的一种深度神经网络。在当时的ImageNet比赛中,它斩获了图像分类第一名、目标检测第一名;在COCO数据集上,也获得了目标检测第一名和图像分割第一名。
1.1 主要特点
- 残差学习机制:传统神经网络每一层的输出直接通过非线性激活函数得到,而ResNet每一层的输出通过“残差块”获得。该残差块包含快捷连接(shortcut)和几个卷积层。在训练过程中,每一层只需学习残差(输入与输出之间的差异),而非所有信息,有助于防止梯度消失和梯度爆炸问题,使网络能够训练得更深。
- 网络结构与训练速度:网络结构相对简单,训练速度比GoogLeNet快,因此成为许多计算机视觉任务的首选模型。
1.2 主要优点
- 层数与训练效率:具有非常深的层数,可达1000多层,仍能高效训练。通过残差连接,模型可学习跨越多个层的残差,而非直接学习每一层的输出,从而能更快收敛,且能更好地泛化到新数据集。
1.3 论文信息
- 论文名称:Deep Residual Learning for Image Recognition
- 论文地址:ResNet_Paper
1.4 网络结构
论文中共提出了五种结构,分别是ResNet - 18、ResNet - 34、ResNet - 50、ResNet - 101、ResNet - 152。
二、网络的结构
在paper中给出了网络结构的表,如下图所示: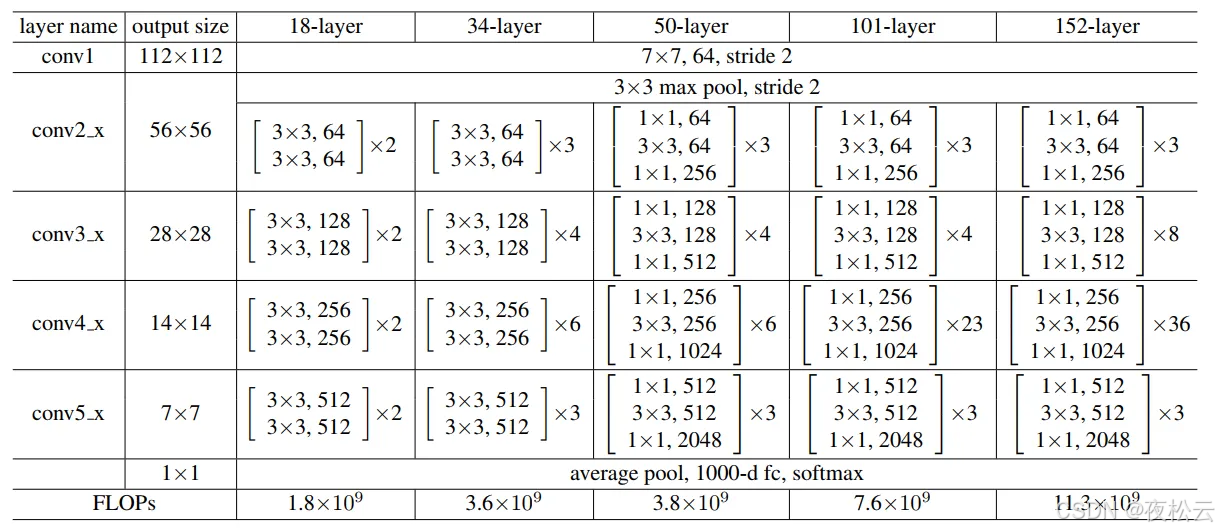
残差连接的34 层网络结构图
三、网络的创新
3.1 更深的网络层数带来的问题
在搭建更深的网络时,不能像常规那样直接进行卷积和池化的堆叠。直接堆叠网络会出现错误率异常的情况,具体表现如下: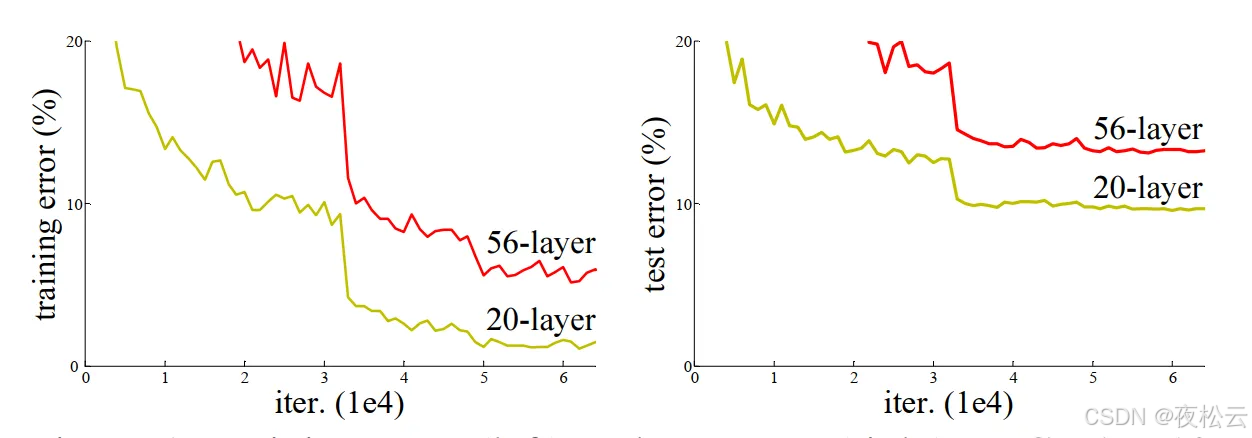
通过直接堆叠神经网络的实验结果图可知,在左侧图中,黄色线是训练过程中 20 层网络的训练损失曲线,红色线是训练过程中 56 层网络的训练损失曲线。理论上,网络更深应带来更小的损失,但实际相反,56 层网络的错误率高于 20 层网络。
出现这种情况的原因主要有以下两点:
- 梯度消失或梯度爆炸
- 梯度消失:在一个网络中,若每一层的损失梯度的值都小于 1,根据连续的链式法则,每进行一次前向传播,都要乘以一个小于 1 的误差梯度。网络越深,经过大量前向传播后,梯度会越来越小,直至接近于 0,这就是梯度消失现象。
- 梯度爆炸:若每一层的损失梯度的值都大于 1,网络越深,经过大量前向传播后,梯度会越来越大,从而导致梯度爆炸。
- 应对措施及问题:误差梯度通常不会始终为 1 或接近 1,一般可通过数据标准化处理、权重初始化等操作来抑制梯度消失或爆炸问题。此外,Relu 函数也能抑制梯度消失问题,但它可能会导致原始特征不可逆损失,进而引出网络退化问题。
- 退化问题(degradation problem)
随着网络层数的增多,训练集的损失(loss)会先逐渐下降,然后趋于饱和。当继续增加网络深度时,训练集的损失反而会增大。需要注意的是,这并非过拟合现象,因为过拟合时训练损失是一直减小的。
3.2 Residual结构(残差结构)
3.2.1 残差结构效果
使用残差结构进行网络组合时,可明显解决相关问题。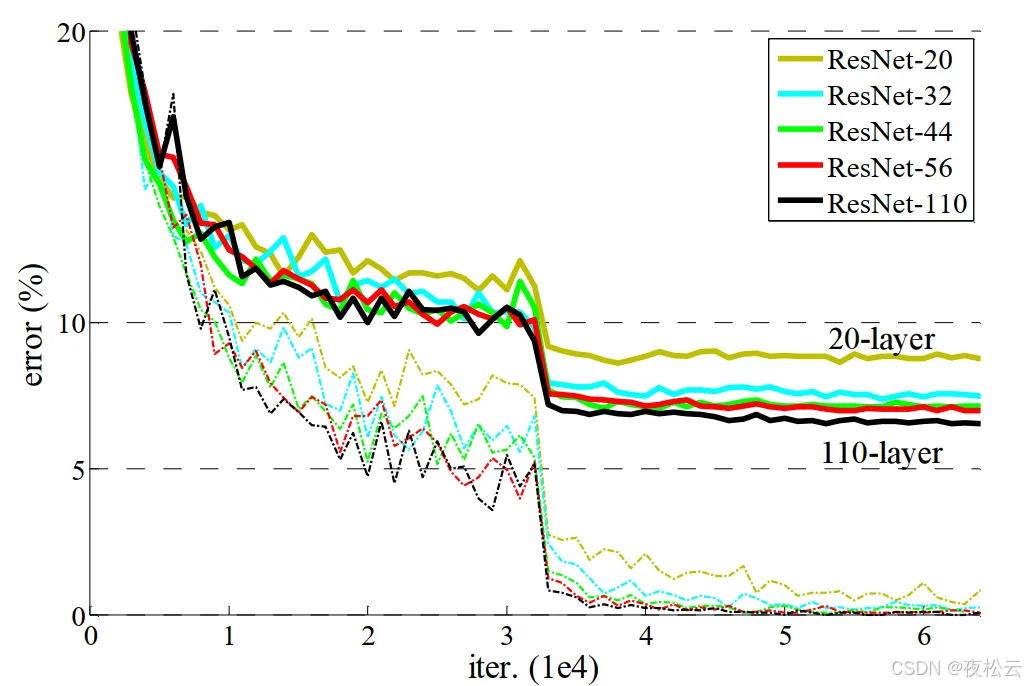
从对应图示能看出,使用残差结构后,网络层数从20层增加到110层,错误率逐步降低。这表明残差网络对退化问题(degradation problem)有抑制作用,其原理在于使用残差网络后,模型内部复杂度降低,进而抑制了退化问题。
3.2.2 ResNet网络两种不同的残差结构
Residual结构即残差结构,存在两种不同形式。在ResNet - 18和ResNet - 34中,采用如下图左侧所示的结构;在ResNet - 50、ResNet - 101和ResNet - 152中,使用的是下图右侧的结构。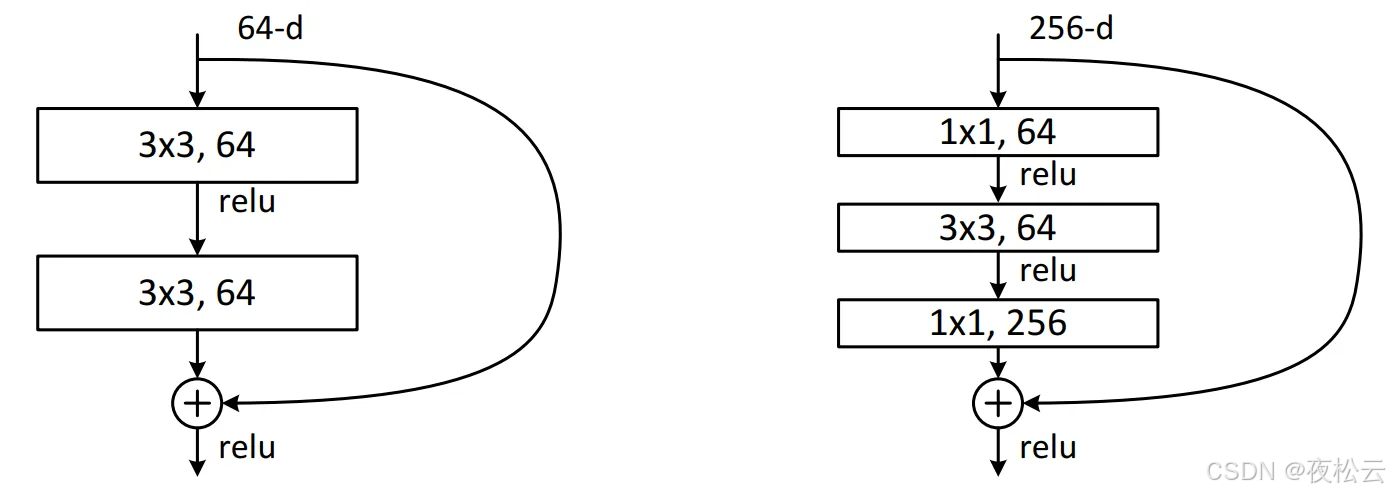
- 左侧结构(适用于ResNet - 18和ResNet - 34):输入特征矩阵的channels为64,先经过一个3x3的卷积核卷积,接着通过Relu激活函数激活,再经过一个3x3的卷积核卷积,但此次卷积后不直接进行激活。主分支上有一条从输入特征矩阵直接连到加号的圆弧线,即shortcut(捷径分支),它将输入特征矩阵直接加到第二次3x3卷积核卷积后的输出特征矩阵上,这里是矩阵对应维度位置进行加法运算,要求主分支的输出矩阵和shortcut的输出矩阵的shape(包括宽、高、channels)必须相同,相加后再经过Relu激活函数激活。
- 右侧结构(适用于ResNet - 50、ResNet - 101和ResNet - 152):输入特征矩阵的channels为256,先经过一个1x1的卷积进行降维到64(1x1卷积可用于维度变换),然后用3x3的卷积进行特征提取,提取完成后,再通过1x1的卷积进行升维到256,得到的输出矩阵与经过shortcut的输入矩阵进行对应维度位置的加法运算,相加后经过Relu激活函数激活。
3.2.3 ResNet神经网络结构处理特征矩阵变化问题
在神经网络中,特征矩阵的channels可能不断增大,宽和高也可能变为原来的一半,导致主分支和shortcut的输出特征矩阵shape不同。以ResNet - 34的网络结构为例,其残差网络部分的shortcut有实线和虚线之分。
- 实线部分:当主分支的输入特征矩阵和输出特征矩阵的shape一致时,输入特征矩阵经过shortcut得到的输出特征矩阵可直接与主分支的输出特征矩阵进行加法运算,如左侧图所示。
- 虚线部分:不仅有channels变化,还有特征矩阵宽和高的变化。需要进行下采样(downsampling)处理,即通过卷积缩小图片,使主分支的输出特征矩阵和shortcut的输出特征矩阵保持一致。
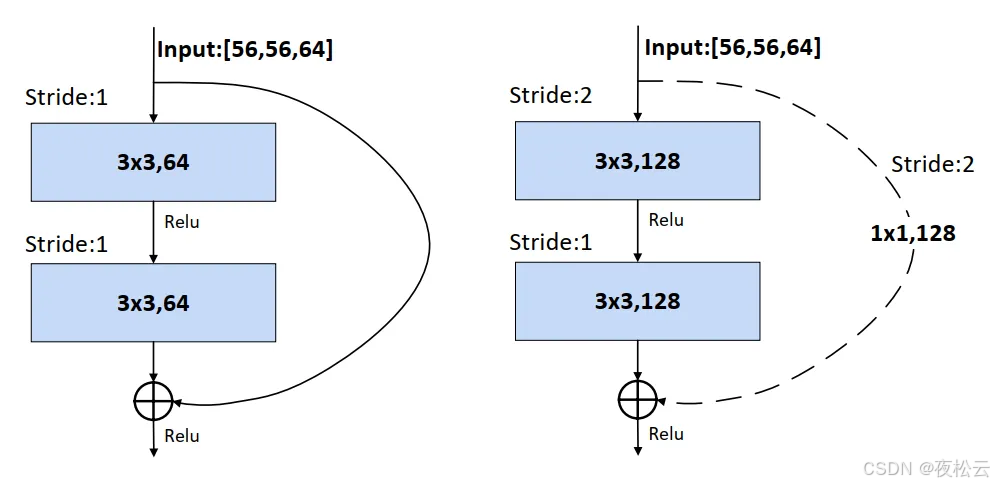
例如右侧图中,主分支因步长 = 2,矩阵的宽和高减半,同时第一个卷积核个数为128,使channels从64升到128,主分支输出特征矩阵为[28, 28, 128],此时在shortcut分支上加一个卷积运算,卷积核个数为128,步长为2,使shortcut分支的输出矩阵也为[28, 28, 128],两个输出矩阵便可相加。
3.2.4 残差结构抑制degradation problem问题的原因
残差网络结构可表示为 H ( x ) = F ( x ) + x H(x)=F(x)+x H(x)=F(x)+x,其中 x x x是shortcut的输出特征矩阵(通常等于输入特征矩阵), F ( x ) F(x) F(x)是主分支的输出特征矩阵。
对 H ( x ) H(x) H(x)求关于 w w w的偏导数可得 ∂ H ( x ) ∂ w = ∂ F ( x ) ∂ w + ∂ x ∂ w {\frac{\partial H(x)}{\partial w}={\frac{\partial F(x)}{\partial w}}+{\frac{\partial x}{\partial w}}} ∂w∂H(x)=∂w∂F(x)+∂w∂x,这表明残差结构的反向传播不仅与主分支 F ( x ) F(x) F(x)有关,还与 x x x有关。当主分支卷积层的导数很小时,对网络更新作用不大,但由于加入了输入矩阵的导数,保证了网络导数一直存在,不会出现导数消失的情况。
简而言之,ResNet网络中残差结构的堆叠过程类似:前几个残差结构提取重要特征,后几个残差结构对特征进行细化。即使后几个残差结构学不到东西,也不会影响前面的梯度,从而避免degradation problem退化问题。
3.3 Batch Normalization
3.3.1 概念
对一个batch内的数据在通道尺度上计算均值和方差,将同批次同通道的数据归一化为均值为0、方差为1的正态分布。
3.3.2 为什么要进行Batch Normalization
神经网络在输入图像前通常会对图像进行预处理(如标准化处理),使输入数据满足某一分布规律,从而加速网络的收敛。然而,尽管输入第一次卷积时数据满足某一分布规律,但在输入第二次卷积及后续卷积时,数据可能不再满足该分布规律。因此,需要一个“中间商”,让上一层的输出经过它之后能够满足某一分布规律,Batch Normalization就起到了这样的作用,它可以使输入的特征矩阵的每一个通道满足均值为0、方差为1的分布规律。
例如,对于一张RGB图像,有三个通道,设 x ( 1 ) x^{(1)} x(1)是R对应的特征矩阵, x ( 2 ) x^{(2)} x(2)是G对应的特征矩阵, x ( 3 ) x^{(3)} x(3)是B对应的特征矩阵。以下是求解Batch Normalization的公式:
- 均值: μ = 1 m ⋅ ∑ i = 1 m x i \mu = \frac{1}{m} \cdot \sum_{i = 1}^{m}x_{i} μ=m1⋅∑i=1mxi
- 方差: σ 2 = 1 m ⋅ ∑ i = 1 m ( x i − μ ) 2 \sigma^{2} = \frac{1}{m} \cdot \sum_{i = 1}^{m}(x_{i} - \mu)^{2} σ2=m1⋅∑i=1m(xi−μ)2
- 标准化数值: x ^ i = x i − μ σ 2 + ϵ \hat{x}_{i} = \frac{x_{i} - \mu}{\sqrt{\sigma^{2} + \epsilon}} x^i=σ2+ϵxi−μ,其中 ϵ \epsilon ϵ是为了防止分母为0。
如下图所示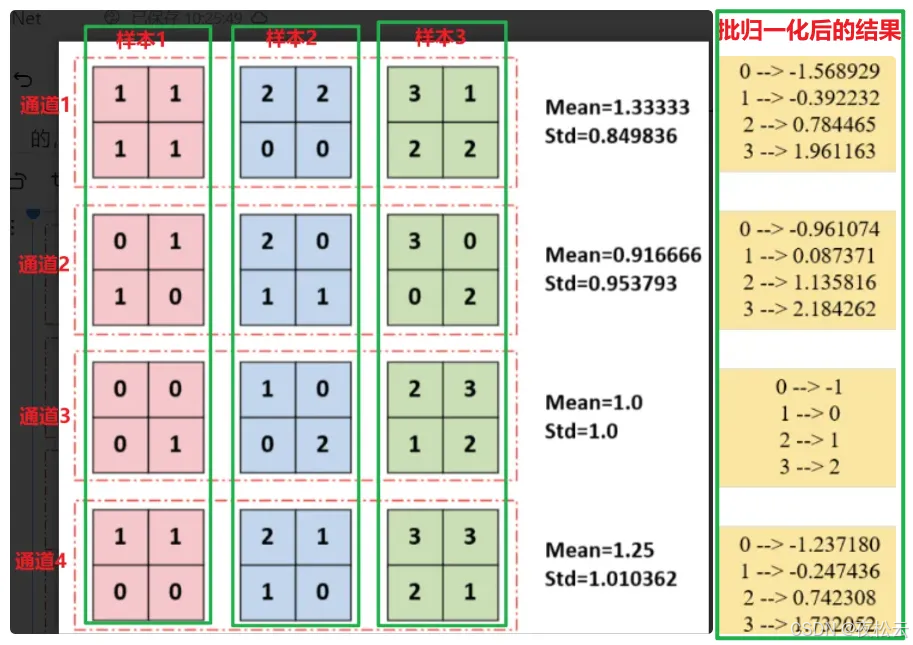
展示了大小为[3, 4, 2, 2](批次大小为3,通道数为4,高为2,宽为2)的tensor的BatchNorm过程,该过程针对训练数据且无缩放和平移。可以看出,BatchNorm是对同一批次内同一通道的所有数据进行归一化。
2.2.3 Batch Normalization的好处
- Batch Normalization有助于抑制梯度消失或梯度爆炸问题。
- 归一化可理解为规则化,使数据符合某些特征,便于模型训练时掌握数据规律。
四、网络问题
- ResNet结构复杂,训练时间较长
- 因其层数极深,需要大量数据用于训练。
五、代码实现
5.1 调用torchvision中的已经写好的resnet代码
# 从torchvision库中导入预定义的ResNet-34模型
from torchvision.models import resnet34
# 从torchsummary库中导入summary函数,用于打印模型的详细信息,如每层的输出形状和参数数量
from torchsummary import summary
import torch
# 检查当前环境是否支持CUDA(NVIDIA GPU加速计算平台)
# 如果支持,则使用CUDA设备;否则,使用CPU设备
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 实例化ResNet-34模型
# 这里创建了一个默认配置的ResNet-34模型
model = resnet34().to(device)
# 将模型移动到之前确定的设备(GPU或CPU)上
# 使用summary函数打印模型的详细信息
# input_size指定输入数据的形状,这里表示输入数据是3通道、224x224大小的图像
# summary函数会遍历模型的每一层,计算并打印每层的输出形状和参数数量
print(summary(model, input_size=(3, 224, 224)))
5.2 手搓代码
import torch #导入torch包,用来进行计算
import torch.nn as nn #导入nn包,用来构建网络
from torchsummary import summary #导入summary包,用来显示网络结构
class BasicBlock(nn.Module): #定义BasicBlock类,它是ResNet中基础的残差块,适用于ResNet18和ResNet34
expansion = 1 #扩展系数,BasicBlock输出通道数与输入通道数相同,所以扩展系数为1
def __init__(self, inplanes, planes, stride=1, downsample=None): #构造函数
#inplanes:输入通道数,planes:输出通道数,stride:步长,downsample:下采样模块
super(BasicBlock, self).__init__() #调用父类nn.Module的构造函数
self.conv1 = nn.Conv2d(
in_channels=inplanes, out_channels=planes, kernel_size=3, stride=stride, padding=1, bias=False
) #第一个卷积层,输入通道数为inplanes,输出通道数为planes,卷积核大小为3,步长为stride,填充为1,不使用偏置
self.bn1 = nn.BatchNorm2d(planes) #第一个批量归一化层,对卷积层的输出进行归一化处理
self.relu = nn.ReLU(inplace=True) #ReLU激活函数,inplace=True表示直接在原数据上进行修改,节省内存
self.conv2 = nn.Conv2d(
in_channels=planes, out_channels=planes, kernel_size=3, stride=1, padding=1, bias=False
) #第二个卷积层,输入通道数和输出通道数都为planes,卷积核大小为3,步长为1,填充为1,不使用偏置
self.bn2 = nn.BatchNorm2d(planes) #第二个批量归一化层
self.downsample = downsample #下采样模块,用于处理捷径分支与主分支维度不匹配的情况
def forward(self, x): #前向传播函数
identity = x #保存输入作为捷径分支的输入
out = self.conv1(x) #经过第一个卷积层
out = self.bn1(out) #经过第一个批量归一化层
out = self.relu(out) #经过ReLU激活函数
out = self.conv2(out) #经过第二个卷积层
out = self.bn2(out) #经过第二个批量归一化层
if self.downsample is not None: #如果存在下采样模块,对捷径分支进行下采样
identity = self.downsample(x)
out += identity #将主分支和捷径分支的输出相加
out = self.relu(out) #经过ReLU激活函数
return out #返回输出
class Bottleneck(nn.Module): #定义Bottleneck类,它是ResNet中用于更深网络(如ResNet50及以上)的残差块
expansion = 4 #扩展系数,Bottleneck输出通道数是输入通道数的4倍
def __init__(self, inplanes, planes, stride=1, downsample=None): #构造函数
#inplanes:输入通道数,planes:输出通道数,stride:步长,downsample:下采样模块
super(Bottleneck, self).__init__() #调用父类nn.Module的构造函数
self.conv1 = nn.Conv2d(
in_channels=inplanes, out_channels=planes, kernel_size=1, stride=1, bias=False
) #第一个卷积层,使用1x1卷积进行降维,输入通道数为inplanes,输出通道数为planes,步长为1,不使用偏置
self.bn1 = nn.BatchNorm2d(planes) #第一个批量归一化层
self.conv2 = nn.Conv2d(
in_channels=planes, out_channels=planes, kernel_size=3, stride=stride, padding=1, bias=False
) #第二个卷积层,使用3x3卷积提取特征,输入通道数和输出通道数都为planes,步长为stride,填充为1,不使用偏置
self.bn2 = nn.BatchNorm2d(planes) #第二个批量归一化层
self.conv3 = nn.Conv2d(
in_channels=planes, out_channels=planes * self.expansion, kernel_size=1, stride=1, bias=False
) #第三个卷积层,使用1x1卷积进行升维,输入通道数为planes,输出通道数为planes * self.expansion,步长为1,不使用偏置
self.bn3 = nn.BatchNorm2d(planes * self.expansion) #第三个批量归一化层
self.relu = nn.ReLU(inplace=True) #ReLU激活函数
self.downsample = downsample #下采样模块,用于处理捷径分支与主分支维度不匹配的情况
def forward(self, x): #前向传播函数
identity = x #保存输入作为捷径分支的输入
out = self.conv1(x) #经过第一个卷积层
out = self.bn1(out) #经过第一个批量归一化层
out = self.relu(out) #经过ReLU激活函数
out = self.conv2(out) #经过第二个卷积层
out = self.bn2(out) #经过第二个批量归一化层
out = self.relu(out) #经过ReLU激活函数
out = self.conv3(out) #经过第三个卷积层
out = self.bn3(out) #经过第三个批量归一化层
if self.downsample is not None: #如果存在下采样模块,对捷径分支进行下采样
identity = self.downsample(x) #让捷径分支与主分支的维度相同
out += identity #将主分支和捷径分支的输出相加
out = self.relu(out) #经过ReLU激活函数
return out #返回输出
class ResNet(nn.Module): #定义ResNet类,它是整个ResNet网络的核心类
def __init__(self, block, layers, num_classes=1000): #构造函数
#block:残差块,layers:残差块的数量,num_classes:分类数
super(ResNet, self).__init__() #调用父类nn.Module的构造函数
self.inplanes = 64 #输出通道数
self.conv1 = nn.Conv2d(
in_channels=3, out_channels=64, kernel_size=7, stride=2, padding=3, bias=False
) #第一个卷积层,输入通道数为3(RGB图像),输出通道数为64,卷积核大小为7,步长为2,填充为3,不使用偏置
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1) #最大池化层,用于缩小特征图的尺寸
self.bn1 = nn.BatchNorm2d(64) #第一个批量归一化层
self.relu = nn.ReLU(inplace=True) #ReLU激活函数
self.layer1 = self._make_layer(block, 64, layers[0]) #第一个残差块,输出通道数为64,残差块数量为layers[0]
self.layer2 = self._make_layer(block, 128, layers[1], stride=2) #第二个残差块,输出通道数为128,残差块数量为layers[1]
self.layer3 = self._make_layer(block, 256, layers[2], stride=2) #第三个残差块,输出通道数为256,残差块数量为layers[2]
self.layer4 = self._make_layer(block, 512, layers[3], stride=2) #第四个残差块,输出通道数为512,残差块数量为layers[3]
self.avgpool = nn.AdaptiveAvgPool2d((1, 1)) #自适应平均池化层,将特征图尺寸调整为1x1
self.fc = nn.Linear(512 * block.expansion, num_classes) #全连接层,输入通道数为512 * block.expansion,输出通道数为num_classes
def _make_layer(self, block, planes, blocks, stride=1): #定义_make_layer函数,用于构建残差块
#block:残差块,planes:输出通道数,blocks:残差块数量,stride:步长
downsample = None #下采样模块
if stride != 1 or self.inplanes != planes * block.expansion: #如果步长不为1或者输入通道数不等于输出通道数乘以扩展系数
downsample = nn.Sequential( #下采样模块由一个卷积层和一个批量归一化层组成
nn.Conv2d(
in_channels=self.inplanes, out_channels=planes * block.expansion, kernel_size=1,
stride=stride, bias=False
), #卷积层,输入通道数为self.inplanes,输出通道数为planes * block.expansion,卷积核大小为1,步长为stride,不使用偏置
nn.BatchNorm2d(planes * block.expansion) #批量归一化层
)
layers = [block(self.inplanes, planes, stride, downsample)] #定义一个列表,用于保存残差块
self.inplanes = planes * block.expansion #更新输入通道数
for _ in range(1, blocks): #添加剩余的残差块
layers.append(block(self.inplanes, planes))
return nn.Sequential(*layers) #将列表转换为Sequential模块
def forward(self, x): #前向传播函数
x = self.conv1(x) #经过第一个卷积层
x = self.bn1(x) #经过第一个批量归一化层
x = self.relu(x) #经过ReLU激活函数
x = self.maxpool(x) #经过最大池化层
x = self.layer1(x) #经过第一个残差块
x = self.layer2(x) #经过第二个残差块
x = self.layer3(x) #经过第三个残差块
x = self.layer4(x) #经过第四个残差块
x = self.avgpool(x) #经过自适应平均池化层
x = torch.flatten(x, 1) #展平特征图
x = self.fc(x) #经过全连接层
return x #返回输出
def resnet18(num_class=1000): #定义resnet18函数,返回一个ResNet18模型
return ResNet(BasicBlock, layers=[2, 2, 2, 2], num_classes=num_class) #使用BasicBlock构建ResNet18
def resnet34(num_class=1000): #定义resnet34函数,返回一个ResNet34模型
return ResNet(BasicBlock, layers=[3, 4, 6, 3], num_classes=num_class) #使用BasicBlock构建ResNet34
def resnet50(num_class=1000): #定义resnet50函数,返回一个ResNet50模型
return ResNet(Bottleneck, layers=[3, 4, 6, 3], num_classes=num_class) #使用Bottleneck构建ResNet50
def resnet101(num_class=1000): #定义resnet101函数,返回一个ResNet101模型
return ResNet(Bottleneck, layers=[3, 4, 23, 3], num_classes=num_class) #使用Bottleneck构建ResNet101
if __name__ == '__main__': #当程序执行时
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') #设置设备
model = resnet18(1000).to(device) #创建ResNet18模型
summary(model, (3, 224, 224)) #打印模型概述
总结
本文围绕ResNet展开了全面而深入的介绍。首先阐述了ResNet的基本信息,包括其提出团队、在相关比赛中的优异表现、主要特点(残差学习机制、网络结构与训练速度优势)、优点(深层数高效训练与良好泛化能力)、论文信息以及网络结构类型。接着详细分析了其网络结构,通过图示直观展示。在创新方面,探讨了更深网络层数带来的梯度消失或爆炸以及退化问题,并介绍了ResNet如何通过残差结构和Batch Normalization解决这些问题。同时也指出了ResNet存在结构复杂、训练时间长以及需要大量训练数据的问题。最后给出了调用torchvision库和手动编写代码两种方式实现ResNet的示例。ResNet以其独特的残差学习机制在深度神经网络领域取得了重大突破,为后续研究和应用奠定了坚实基础。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)