一：理解极限

如下，对于$x=0$附近的取值（除去$x=0$这个点），当取值在其邻域内不断逼近0时，函数值会越来越接近某个值，这个值就是极限

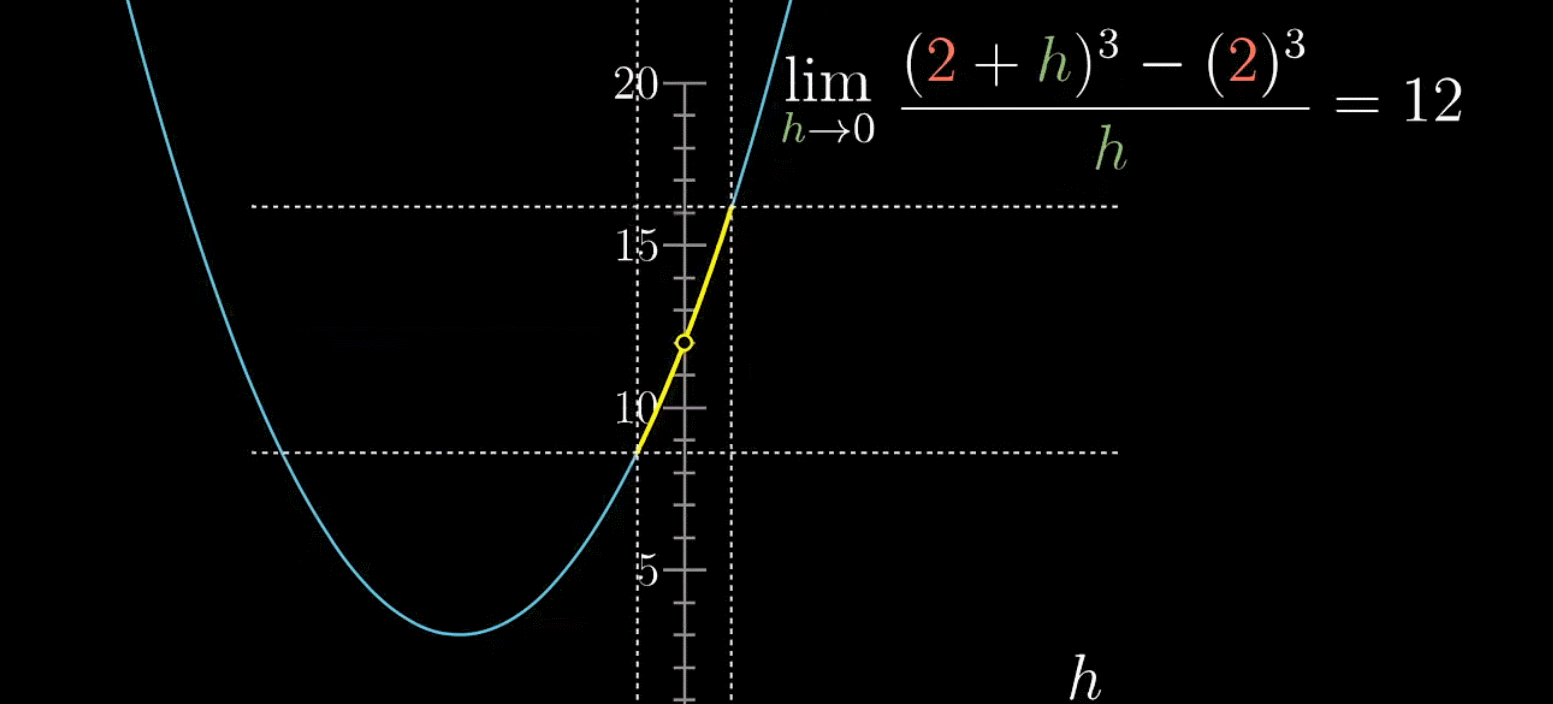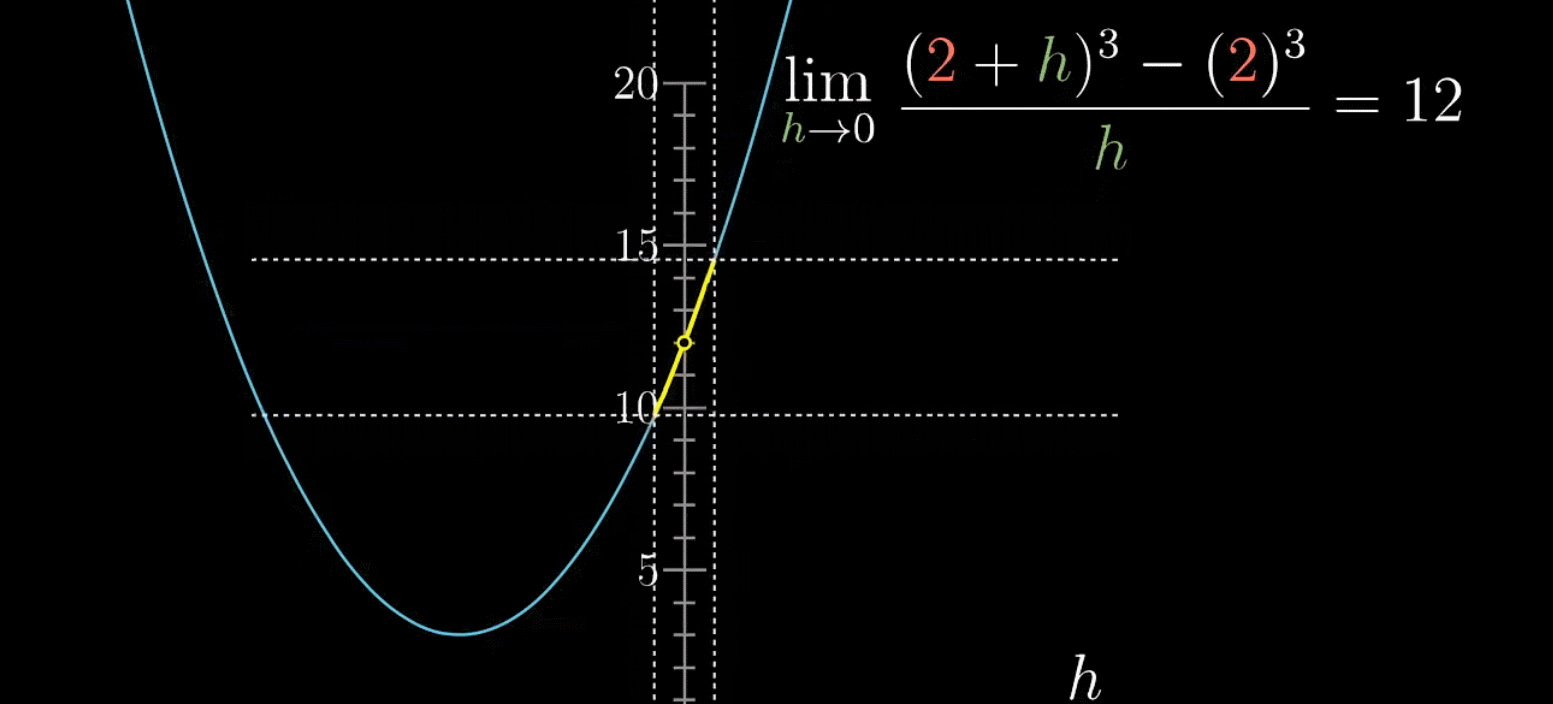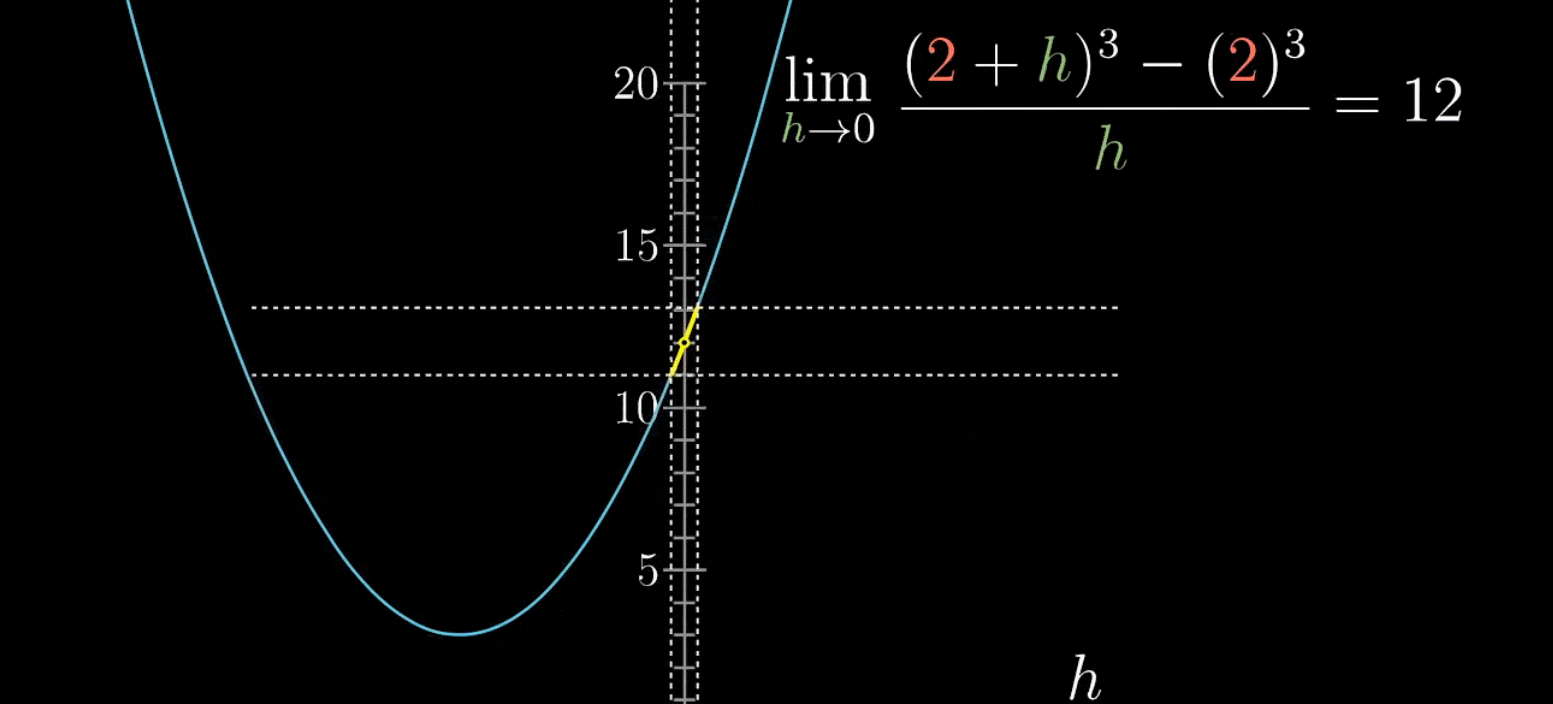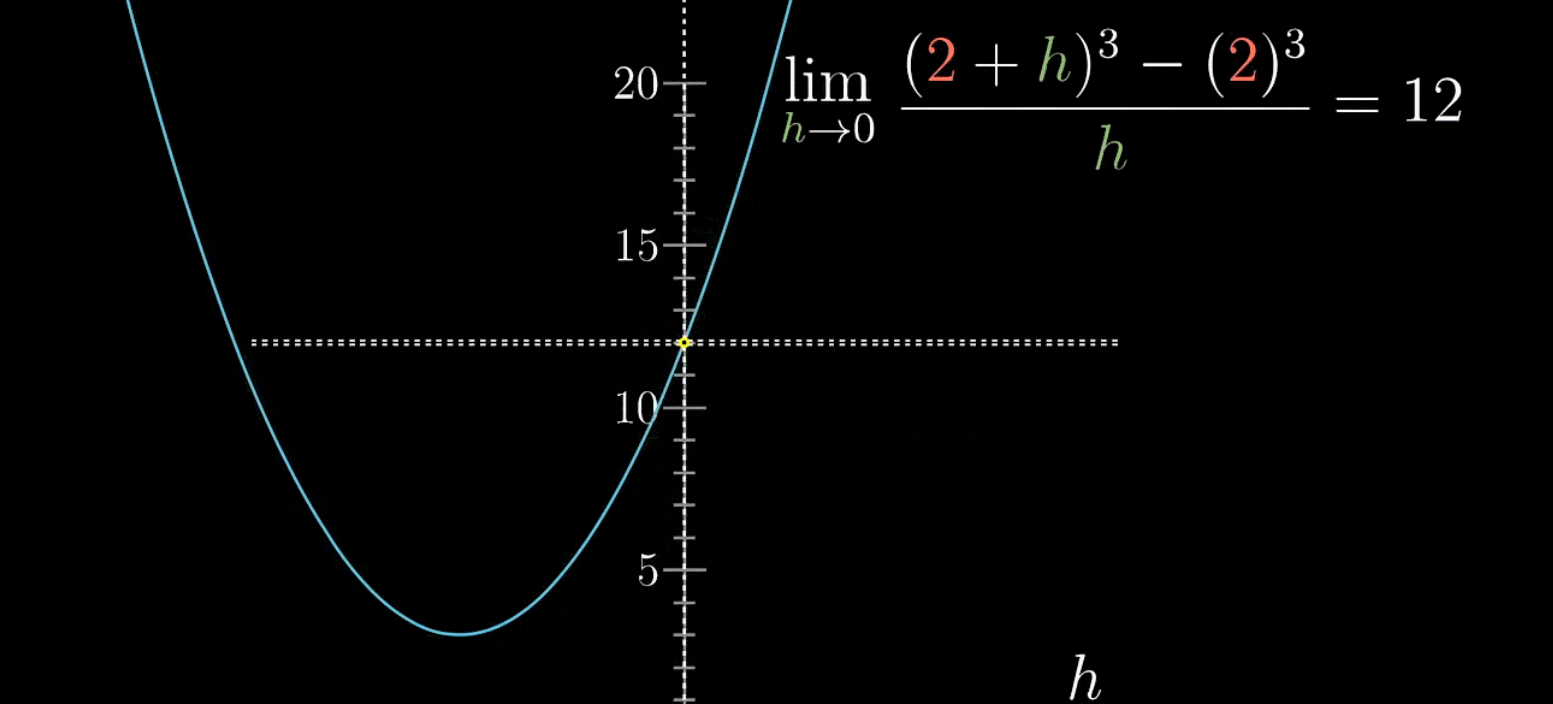
如下情况，极限是不存在的，因为在自变量不断逼近0时，函数值并不会收缩在特定值上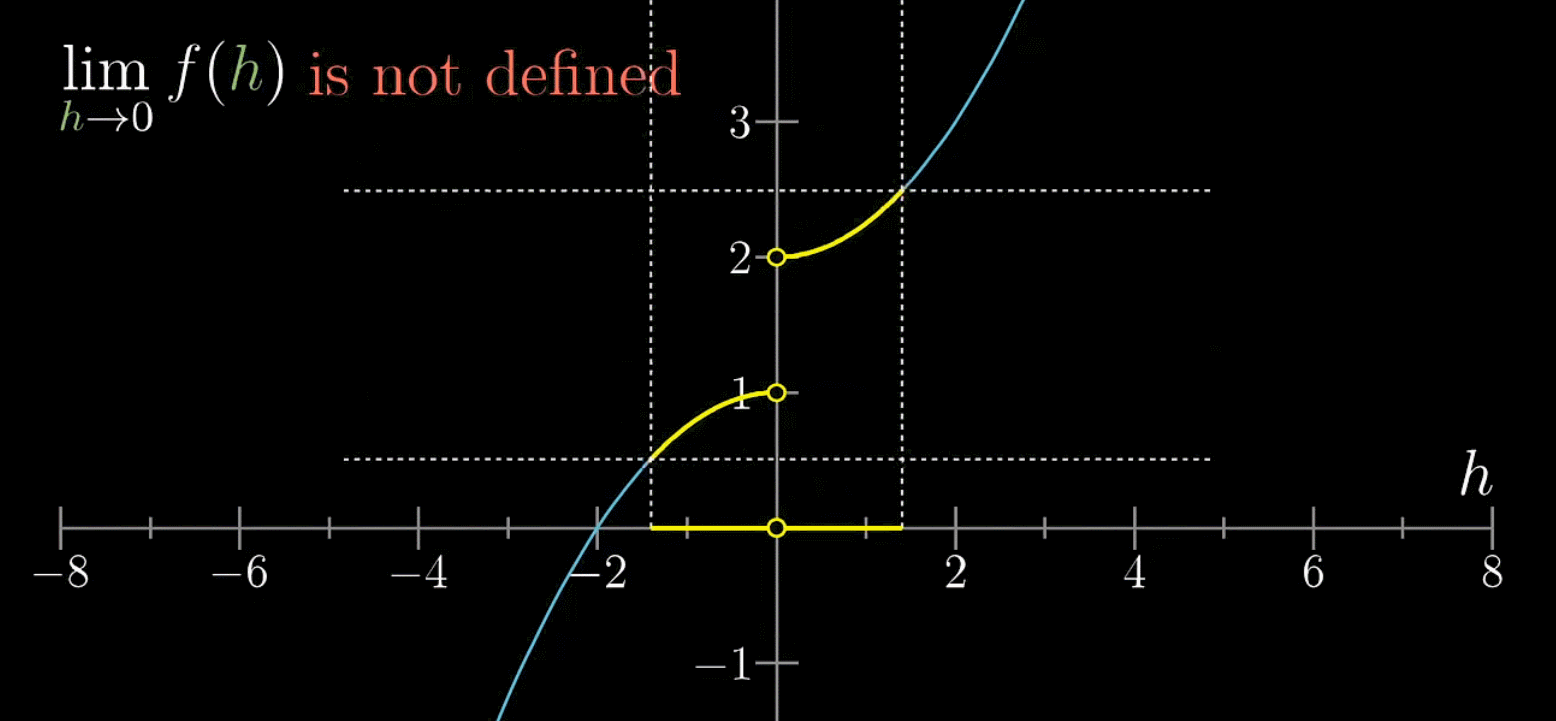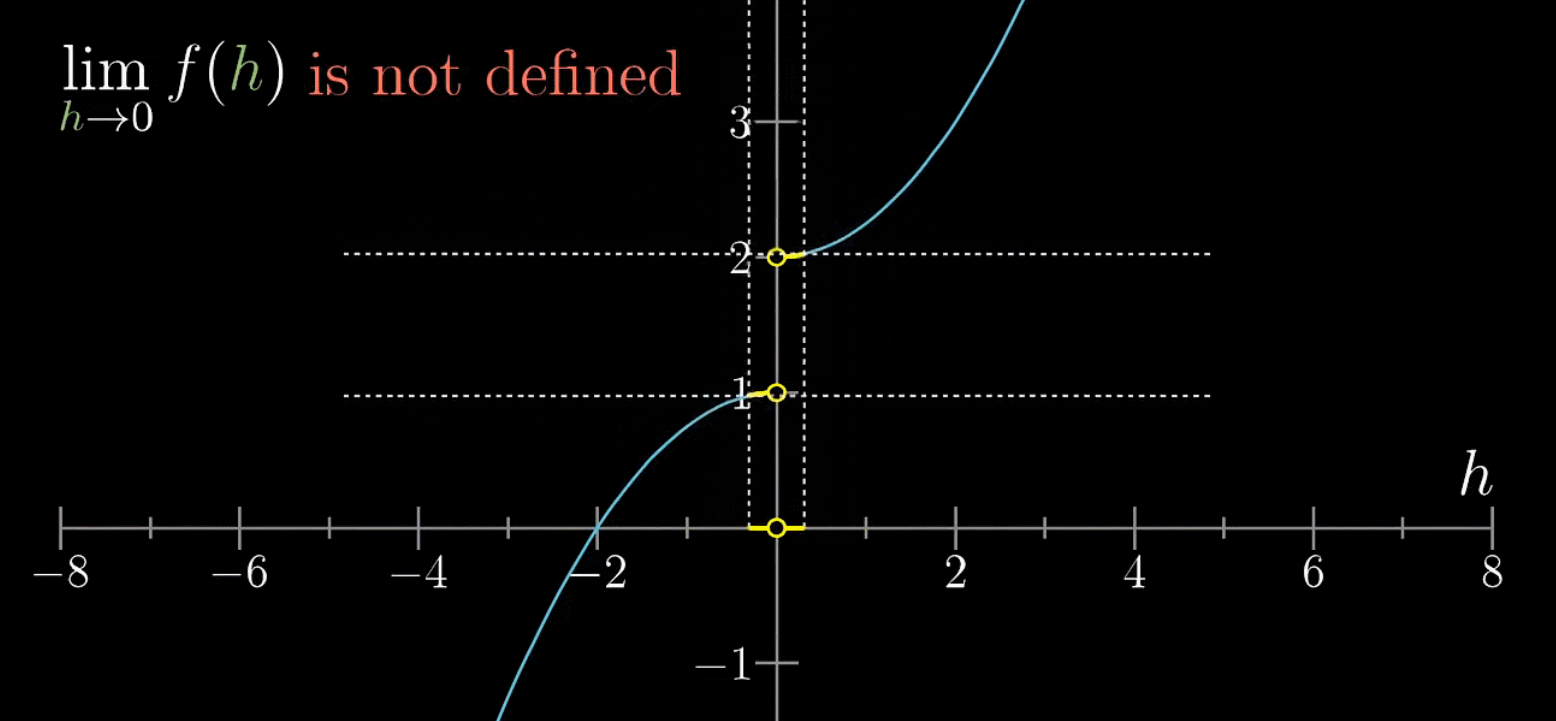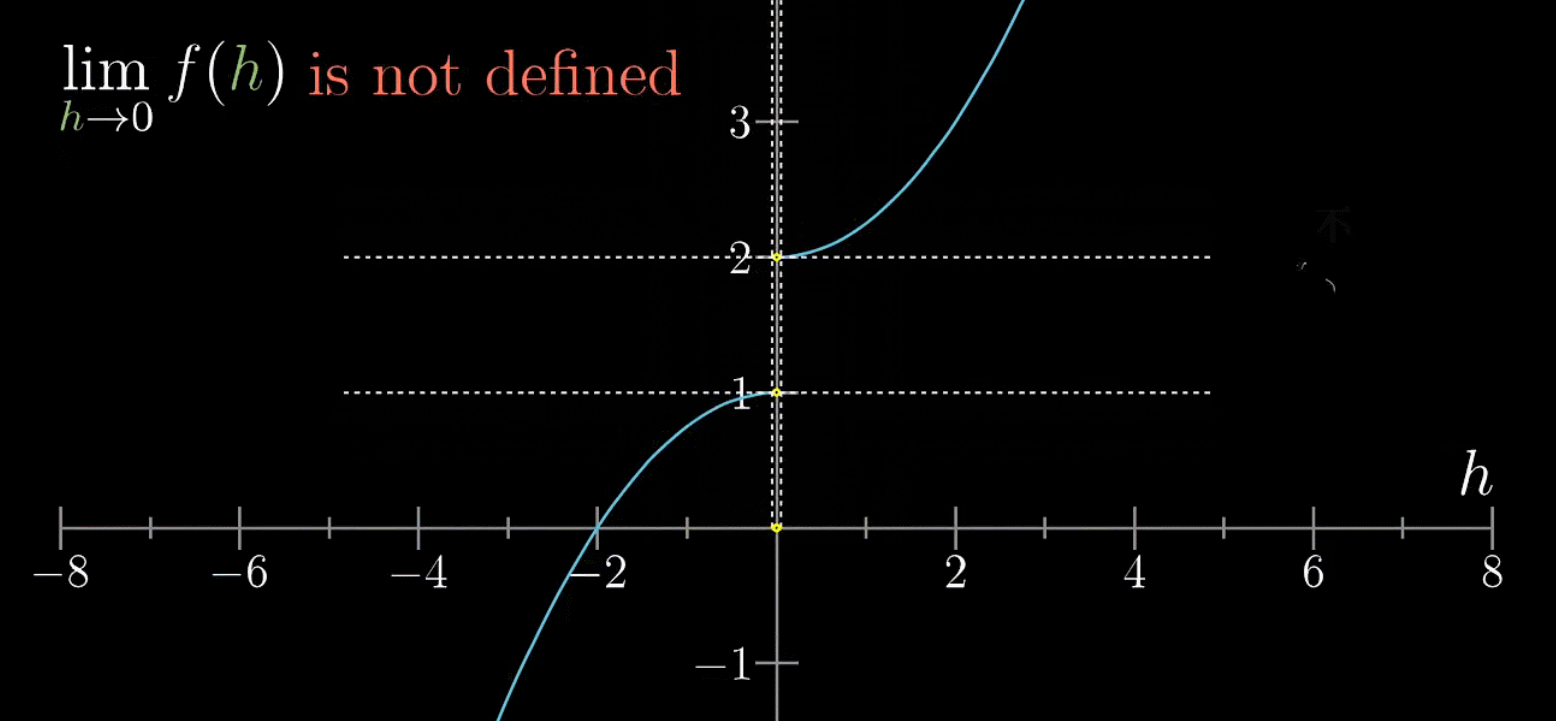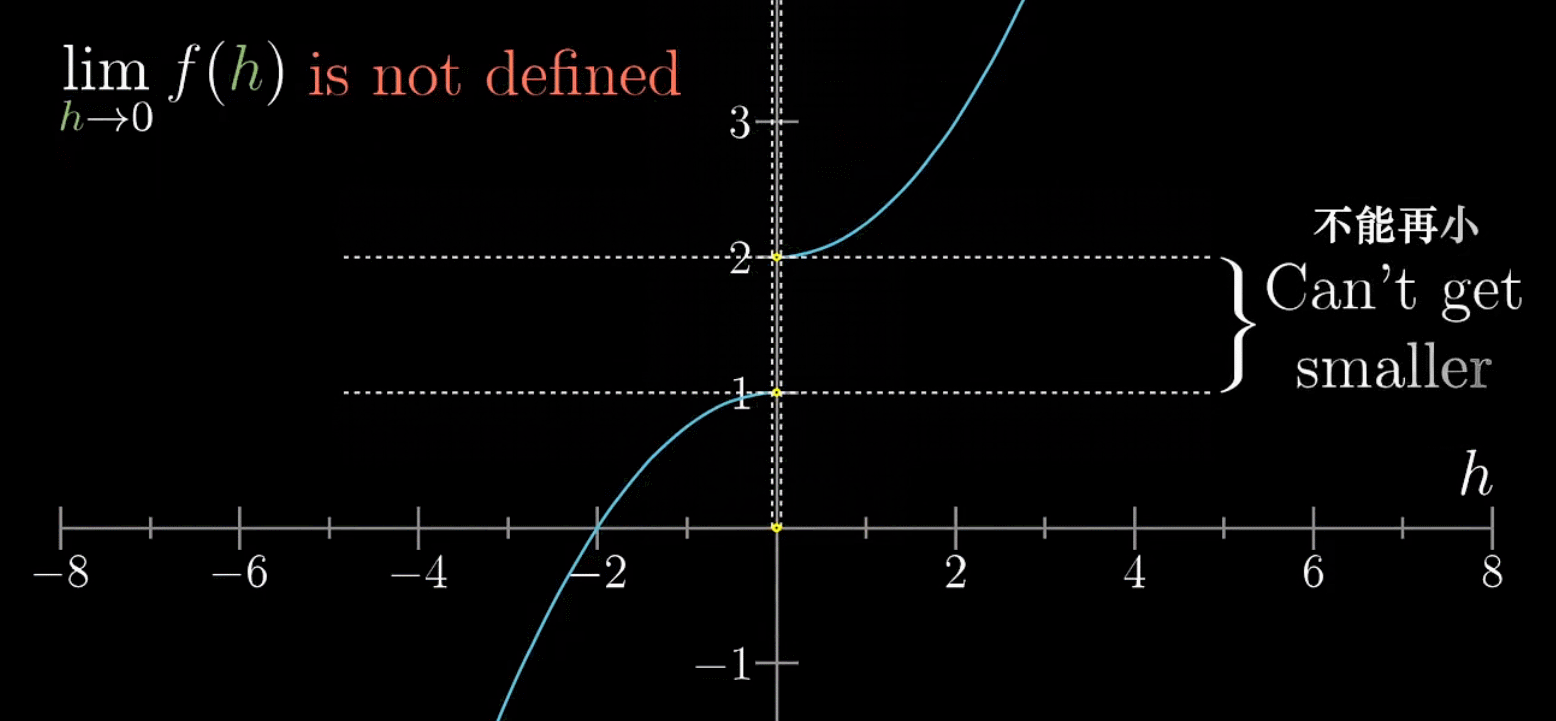

二：极限的概念

（1）数列极限

定义：如果对于任意给定的$\xi >0$，总存在正整数$N$，当$n$>$N$时，恒有$|x_n-a|<\xi$成立，则称常数$a$为数列 { x n } \{x_{n}\} {xn​}当$n$趋于无穷时的极限，即为$\underset{n\to \infty }{\lim }{x}_n=a$

• $\xi$是用来刻画$x_n$与$a$的接近程度；$N$是用来刻画 $n\to \infty$这个极限的过程
• $\underset{n\to \infty }{\lim }{x}_n=a$的几何意义：对于$a$点的任何$\xi$领域也即开区间$(a-\xi ,a+\xi )$，一定存在$N$，当$n>N$也即第$N$项以后的点$x_n$都落在开区间$(a-\xi ,a+\xi )$内，而只有有限个（最多$N$个）落在此区间之外
• 数列 { x n } \{x_{n}\} {xn​}的极限是否存在（或者说存在等于多少）与数列的前有限项无关
• $\underset{n\to \infty }{\lim }{x}_n=a<=>\underset{k\to \infty }{\lim }{x}_{2k-1}=a==\underset{k\to \infty }{\lim }{x}_{2k}=a$

（2）函数极限

定义1：如果对于任意给定的$\xi >0$，总存在$X>0$，当$|x|$>$X$时，恒有$|f(x)-A|<\xi$成立，则称常数$A$为$f(x)$当$x$趋于无穷时的极限，即为$\underset{x\to \infty }{\lim }f(x)=A$

• 极限$\underset{x\to \infty }{\lim }f(x)$存在的充要条件是$\underset{x\to -\infty }{\lim }f(x)$ 和$\underset{x\to +\infty }{\lim }f(x)$ 存在且相等

定义2：如果对于任意给定的$\xi >0$，总存在$\sigma >0$，当$0<|x-x_0|<\sigma$时，恒有$|f(x)-A|<\xi$成立，则称常数$A$为$f(x)$当$x$趋于$x_0$时的极限，即为$\underset{x\to x_0}{\lim }f(x)=A$

• $\xi$是用来刻画$f(x)$与$A$的接近程度；$\sigma$是用来刻画$x\to x_0$这个极限过程
• $x\to x_0$但$x\ne x_0$，也即极限$\underset{x\to x_0}{\lim }f(x)$是否存在（或者说存在这个极限值等于多少）与$f(x)$在$x{=}_0$处有无定义（或者说有定义这个函数值为多少）没有关系

（3）左右极限

左极限：如果对于任意给定的$\xi >0$，总存在$\sigma >0$，当$x_0-\sigma <x<x_0$时，恒有$|f(x)-A|<\xi$成立，则称常数$A$为$f(x)$当$x$趋于$x_0$时的左极限，即为$\underset{x\to x_0^{-}}{\lim }f(x)=A$

左极限：如果对于任意给定的$\xi >0$，总存在$\sigma >0$，当$x_0<x<x_0+\sigma$时，恒有$|f(x)-A|<\xi$成立，则称常数$A$为$f(x)$当$x$趋于$x_0$时的右极限，即为$\underset{x\to x_0^{+}}{\lim }f(x)=A$

关于左右极限常见于以下三种情形

• 分段函数在分界点处的极限
• $e^{\infty }$极限（$e^{\infty }\ne \infty$、$e^{+\infty }=+\infty$、$e^{-\infty }=0$）：例如$\underset{x\to 0}{\lim }{e}^{\frac{1}{x}}$
• $arctan\infty$极限（$arctan(+\infty )=\frac{\pi }{2}$、$arctan(-\infty )=-\frac{\pi }{2}$）：

三：极限的性质

（1）有界性

数列：如果数列 { x n } \{x_{n}\} {xn​}收敛，那么数列 { x n } \{x_{n}\} {xn​}一定有界

• 注意：有界不一定收敛

函数：如果$\underset{x\to x_0}{\lim }f(x)$存在，则$f(x)$在$x_0$某去心邻域有界（局部有界）

• 注意：有界不一定收敛

（2）保号性

数列：设$\underset{n\to \infty }{\lim }{x}_n=A$

• 如果$A>0$（或$A<0$），则存在$N>0$，当$n>N$时，$x_n>0$（或$x_n<0$）
• 如果存在$N>0$，当$n>N$时，$x_n\ge 0$（或$x_n\le 0$），则$A\ge 0$（或$A\le 0$）

函数：设$\underset{x\to x_0}{\lim }f(x)=A$

• 如果$A>0$（或$A<0$），则存在$\sigma >0$，当$x$属于$x_0$的$\sigma$去心邻域时，$f(x)>0$（或$f(x)<0$），也即 极限大于0，函数大于0
• 如果存在$\sigma >0$，当$x$属于$x_0$的$\sigma$去心邻域时，$f(x)\ge 0$（或$f(x)\le 0$），则$A\ge 0$（或$A\le 0$），也即 函数大于0，极限大于等于0

（3）极限值与无穷小之间的关系

极限值与无穷小之间的关系为

$$\underset{x\to x_0}{\lim }f(x)=A<=>f(x)=A+\alpha (x)$$

其中$\lim \alpha (x)=0$

四：极限存在准则

（1）夹逼准则

若存在$N$，当$n>N$时，$x_n\le y_n\le z_n$，且$\underset{n\to \infty }{\lim }{x}_n=\underset{n\to \infty }{\lim }{z}_n=a$，则$\underset{n\to \infty }{\lim }{y}_n=a$

（2）单调有界准则

单增有界数列必定有极限

• 单调增且有上界数列必定有极限
• 单调减且有下界数列必定有极限

五：无穷小

（1）无穷小概念

无穷小：若函数$f(x)$当$x\to x_0$（或$x\to \infty$）时的极限为零，则称$f(x)$为$x\to x_0$（或$x\to \infty$）时的无穷小量

（2）无穷小的比较

设$\lim \alpha (x)=0$、$\lim \beta (x)=0$

• 高阶: 若$\lim \frac{\alpha (x)}{\beta (x)}=0$，则称 $\alpha (x)$是$\beta (x)$的高阶无穷小，记为$\alpha (x)=o(\beta (x))$
• 同阶: 若$\lim \frac{\alpha (x)}{\beta (x)}=C\ne 0$，则称 $\alpha (x)$是$\beta (x)$的同阶无穷小
• 等价: 若$\lim \frac{\alpha (x)}{\beta (x)}=1$，则称 $\alpha (x)$是$\beta (x)$的等价无穷小，记为$\alpha (x)$~$o(\beta (x))$
• 无穷小的阶: 若$\lim \frac{\alpha (x)}{\beta (x{)}^k}=C\ne 0$，则称 $\alpha (x)$是$\beta (x)$的$k$阶无穷小

（3）无穷小的性质

• 有限个无穷小的和仍然是无穷小
• 有限个无穷小的积仍是无穷小
• 无穷小量与有界量的积仍然是无穷小

六：无穷大量

（1）无穷大的概念

无穷大：若函数$f(x)$当$x\to x_0$（或$x\to \infty$）时趋于无穷，则称$f(x)$为$x\to x_0$（或$x\to \infty$）时的无穷大量

（2）常用无穷大

当$x\to \infty$时（函数）：

$$l{n}^{\alpha }x<<x^{\beta }<<a^x（\alpha >0,\beta >0,\alpha >1）$$

当$n\to \infty$时（数列）：

$$l{n}^{\alpha }n<<n^{\beta }<<a^n<<n!<<n^n（\alpha >0,\beta >0,\alpha >1）$$

（3）无穷大与无界变量的关系

无穷大量必为无界变量，但无界变量却不一定是无穷大量

若数列 { x n } \{x_{n}\} {xn​}是无穷大：第$N$项后全部要大

$$\forall M>0,\exists N>0，当n>N时，恒有|x_n|>M$$

若数列 { x n } \{x_{n}\} {xn​}是无界变量：有一项额外大即可
$$\forall M>0,\exists N>0，使|x_n|>M$$