吴恩达深度学习——浅层神经网络
文章目录引言神经网络概览神经网络表示计算神经网路的输出引言本文是吴恩达深度学习第一课:神经网络与深度学习的笔记。神经网络与深度学习主要讨论了如何建立神经网络(包括一个深度神经网络)、以及如何训练这个网络。第一课有以下四个部分,本文是第三部分。深度学习概论神经网络基础浅层神经网络深层神经网络神经网络概览本文将我们学习到如何实现神经网络。在上篇文章中,我们已经知道了逻辑回归模型和计算图之间的关系。这就
文章目录
引言
本文是吴恩达深度学习第一课:神经网络与深度学习的笔记。神经网络与深度学习主要讨论了如何建立神经网络(包括一个深度神经网络)、以及如何训练这个网络。
第一课有以下四个部分,本文是第三部分。
学完了第三部分我们会浅层神经网络实现一个平面分类算法。
神经网络概览
本文将我们学习到如何实现神经网络。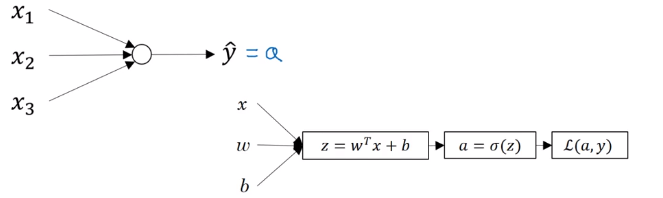
在上篇文章中,我们已经知道了逻辑回归模型和计算图之间的关系。
这就是神经网络,这个神经网络结构中的每个神经元(图中的圈圈),包含了逻辑回归中计算 z z z,然后代入激活函数得到 a a a的过程。
在神经网络中,我们用 x x x表示输入特征,加上参数 W [ 1 ] , b [ 1 ] W^{[1]},b^{[1]} W[1],b[1],可以计算出 z [ 1 ] z^{[1]} z[1]。
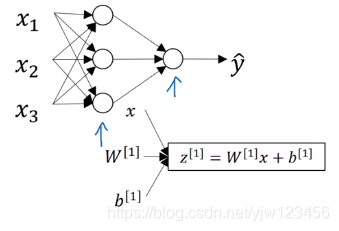
这里我们引入了上标方括号表示与神经元节点(层)相关的量,以便区分表示单个训练样本的圆括号。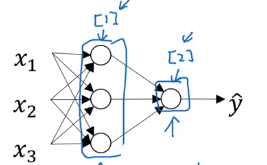
上标方括号里面的数字,表示不同的层,比如 z [ 1 ] z^{[1]} z[1],表示第一层的 z z z值。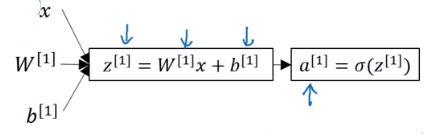
计算出了 z [ 1 ] z^{[1]} z[1]后,然后需要代入激活函数(这里是sigmoid函数)得到 a [ 1 ] a^{[1]} a[1],然后再传递到下一层(相当于重复计算一次逻辑回归)。

然后加上第二层的参数 W [ 2 ] , b [ 2 ] W^{[2]},b^{[2]} W[2],b[2],计算出 a [ 2 ] a^{[2]} a[2],就得到了这个简单的神经网络的输出,然后可以计算损失函数值。
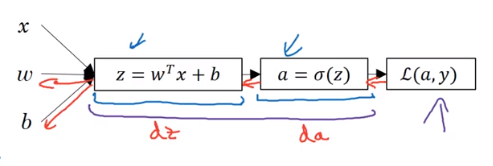
逻辑回归中有红色箭头这种反向传播来计算da,dz,而神经网络中也有类似的反向传播过程。

神经网络表示
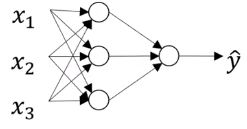
本小节我们来看下神经网络的符号表示,我们还是先看一个简单的只有一个隐藏层的神经网络。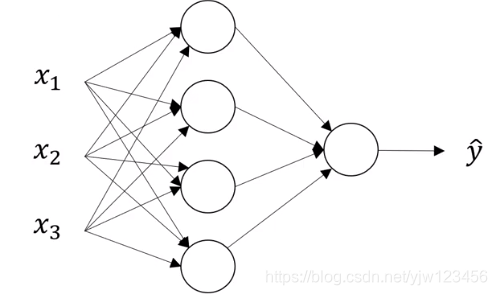
和上一节的神经网络类似,不过隐藏层多了一个神经元。
我们先来了解下神经网络层的命名。
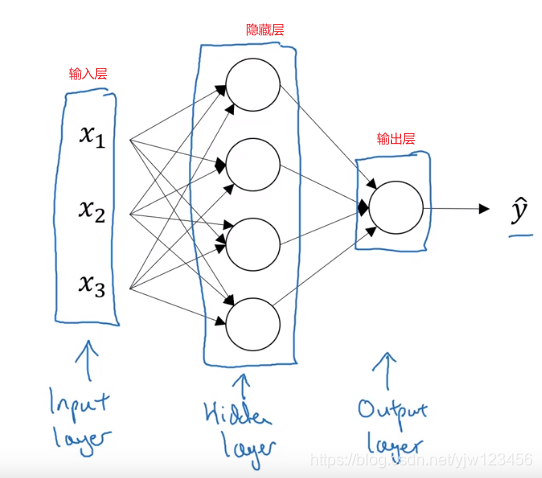
x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3所在的一层代表输入层,输出 y ^ \hat y y^的那一层就是输出层。我们都知道输入层(输入数据)和输出层(真实标签)的值。
我们不知道值的中间那一层(如果是深度神经网络就是中间很多层)就是隐藏层。
我们用 X X X表示输入特征, X X X还可以表示为 a [ 0 ] a^{[0]} a[0]表示第0层的激活值。这个"a"表示激活(activation)的意思,通常表示网络中会传递给下一层的值。
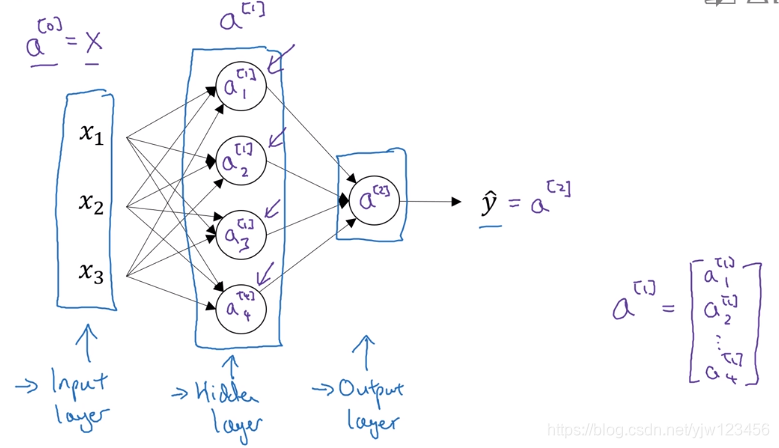
同样地,下一层(隐藏层)的激活值用 a [ 1 ] a^{[1]} a[1]表示,这里隐藏层第一个神经元的激活值用 a 1 [ 1 ] a^{[1]}_1 a1[1]表示。
可以看到 a [ 1 ] a^{[1]} a[1]是一个四维的列向量。
上面其实是一个两层的神经网络,隐藏层是第一层,输出层是第二层,在我们的符号约定中,我们叫输入层为第0层。
一般输入层不计入层数的。
最后,值得一提的是,隐藏层和输出层是带有参数(权值)的。
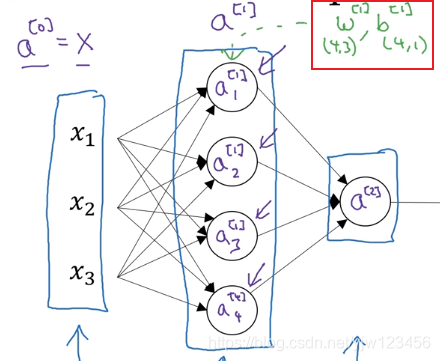
第一个隐藏层有参数 W [ 1 ] , b [ 1 ] W^{[1]},b^{[1]} W[1],b[1]。
W [ 1 ] W^{[1]} W[1]是一个 4 × 3 4\times 3 4×3的矩阵,而 b [ 1 ] b^{[1]} b[1]是一个 4 × 1 4\times 1 4×1的向量。
W [ 1 ] W^{[1]} W[1] 的 4 × 3 4\times 3 4×3 代表有4个节点,3个输入。
同理 W [ 2 ] W^{[2]} W[2]和 b [ 2 ] b^{[2]} b[2]的维度也很好理解。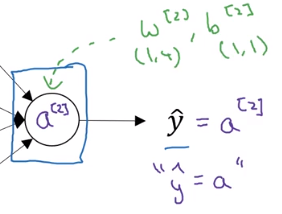
计算神经网路的输出
本节我们来看下神经网络的输出是如何计算出来的。
我们会看到像逻辑回归那样的运算过程被重复多次。
注意,这里说的是单个样本 x x x
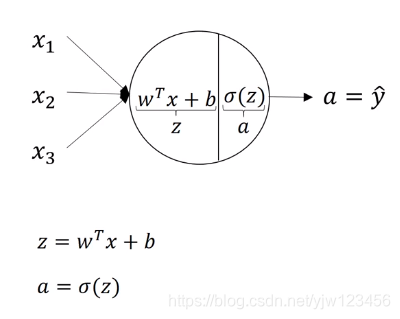
上面是计算逻辑回归的例子,这个圆圈代表了逻辑回归计算的两个步骤:计算 z z z,通过 z z z计算 a a a。
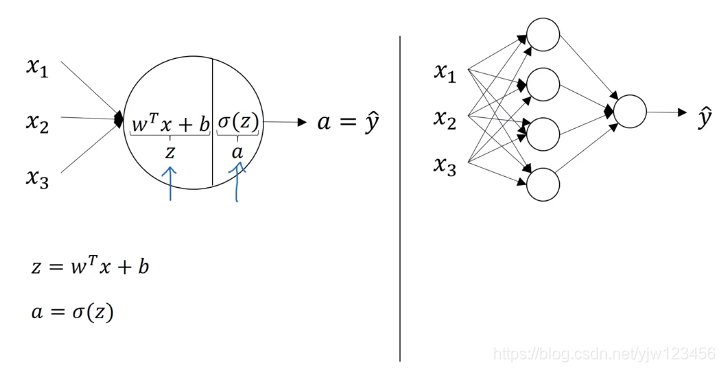
而神经网络不过是重复了这个过程很多次,上图右边的神经网络有很多圆圈,每个圆圈做的事情和左边的圆圈是一样的。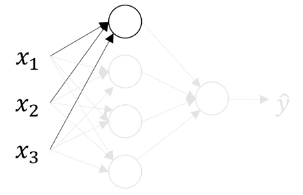
我们先来看下隐藏层的第一个节点。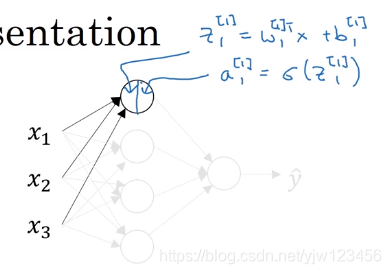
这个圈圈也分成了两步:第一步计算这个节点的 z 1 [ 1 ] z_1^{[1]} z1[1], z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] z_1^{[1]} = w_1^{[1]T}x + b_1^{[1]} z1[1]=w1[1]Tx+b1[1],第二步计算 a 1 [ 1 ] = σ ( z 1 [ 1 ] ) a_1^{[1]} = \sigma(z_1^{[1]}) a1[1]=σ(z1[1])。
值得一提的是,这里的 w 1 [ 1 ] T w_1^{[1]T} w1[1]T表示 ( w 1 [ 1 ] ) T (w_1^{[1]})^T (w1[1])T,左边是一种简写,知道就行了。
再次说明一下,这里的下标 1 1 1表示属于该层的第一个节点,上标 [ 1 ] [1] [1]表示这是第 1 1 1层。
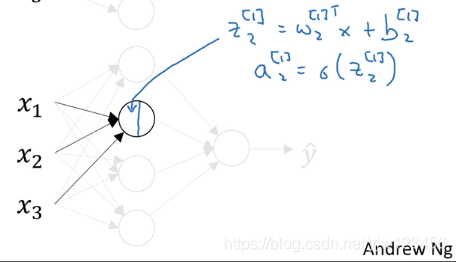
第二个节点也是一样的,计算了两步。以此类推,我们就可以计算出第 1 1 1层的所有 z [ 1 ] z^{[1]} z[1]和 a [ 1 ] a^{[1]} a[1]。

上面我们写出了这些式子,如果要用循环来计算的话肯定十分低效,因此我们需要将这四个等式向量化。
先来看下如何把 z z z当成向量来计算。
我们把 w 1 [ 1 ] T , w 2 [ 1 ] T , w 3 [ 1 ] T , w 4 [ 1 ] T w^{[1]T}_1,w^{[1]T}_2,w^{[1]T}_3,w^{[1]T}_4 w1[1]T,w2[1]T,w3[1]T,w4[1]T堆叠成一个矩阵,得到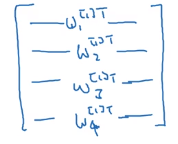
可以看成我们有4个逻辑回归单元,每个逻辑回归单元都有对应的参数向量 w w w( 3 × 1 3 \times 1 3×1),把这些向量堆叠到一起,就得到了这样一个 4 × 3 4\times 3 4×3的矩阵。
如果把这个矩阵乘以输入向量 x x x,就得到了
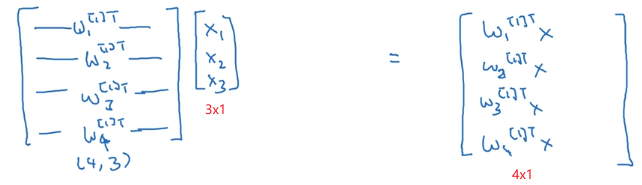
再加上偏置向量 b b b:
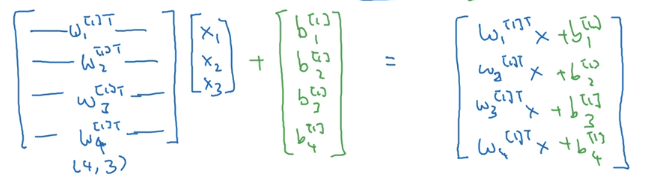
上面最后得到的这个列向量其实就是 z [ 1 ] z^{[1]} z[1]: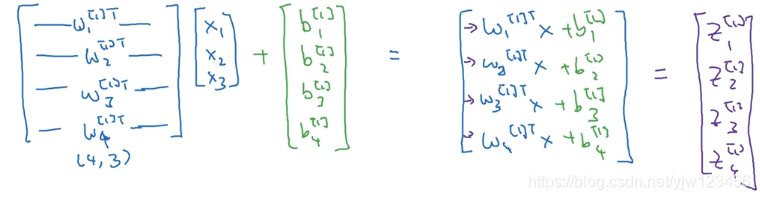
把上面的过程整理一下。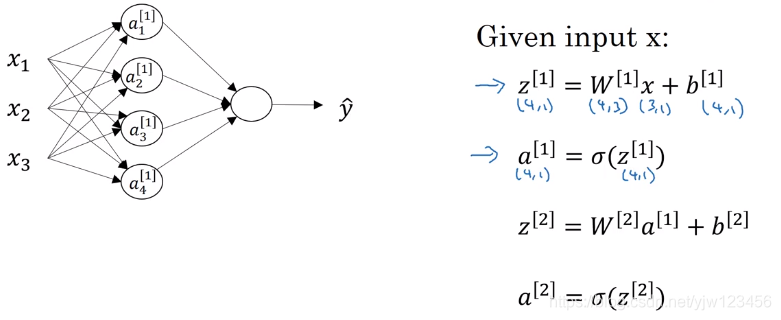
对于神经网络的第一层,给定输入 x x x,根据 W [ 1 ] x + b [ 1 ] W^{[1]}x + b^{[1]} W[1]x+b[1]得到 z [ 1 ] z^{[1]} z[1],代入sigmoid函数得到 a [ 1 ] a^{[1]} a[1]。
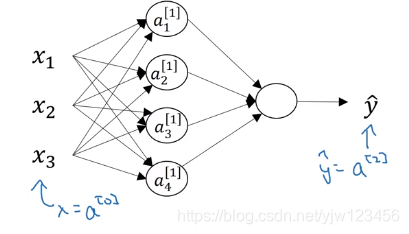
我们知道 x = a [ 0 ] x=a^{[0]} x=a[0], y ^ = a [ 2 ] \hat y = a^{[2]} y^=a[2]。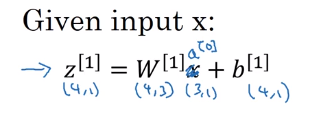
我们就可以把 x x x用 a [ 0 ] a^{[0]} a[0]代替。
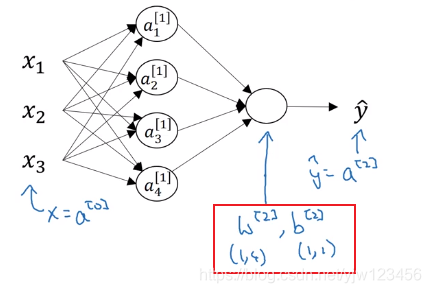
输出层带有的参数是 W [ 2 ] , b [ 2 ] W^{[2]},b^{[2]} W[2],b[2],注意它们的维度。
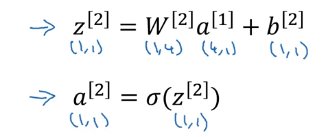
我们只要计算出了下面这四个式子: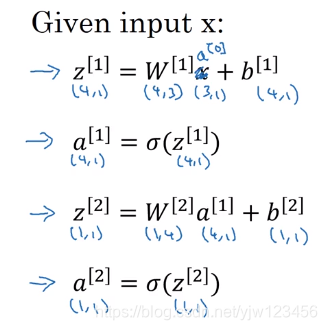
就能得到这个神经网络的输出,我们上面已经向量化了,因此只需要四行代码(也可以放到一个循环里面,不包括for这一行的话,只要两行代码)。
但是就如本节开头说的一样,上面的过程只是计算了单个样本 x x x的输出,我们下节就来看下如何向量化多个样本。
多个样本的向量化
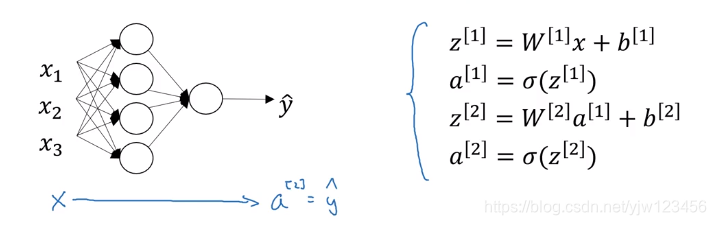
上图是上小节的例子,告诉了我们如何计算单个样本 x x x的输出 y ^ \hat y y^。
那如果有 m m m个训练样本,要如何向量化呢。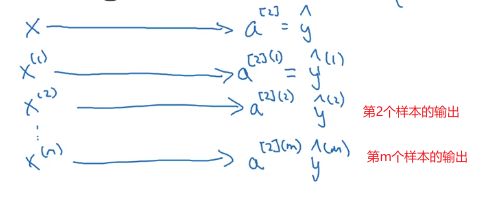
a a a的两个上标中农, ( i ) (i) (i)表示第 i i i个样本, [ 2 ] [2] [2]表示第 2 2 2层。这就是我们使用括号和方括号的意义。
这个过程还是未向量化的,可能需要下面这样编程实现: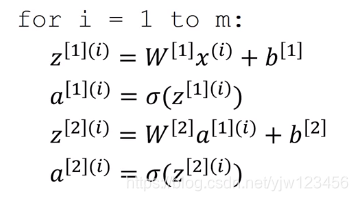
我们要将训练这 m m m个样本的过程向量化,以便加速我们算法的训练速度。
还记得我们矩阵 X X X的定义吗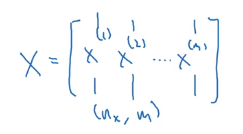
就是把训练样本按列排列,我们只要把上面for循环里面的小写字母(单个样本的向量,除了 b b b)替换为大写字母(多个样本的矩阵)就可以得到向量化的版本,先给出来,后面再分析。
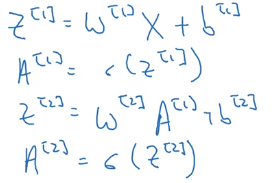
z [ 1 ] z^{[1]} z[1]像 x x x那样堆叠得到 Z [ 1 ] Z^{[1]} Z[1]:
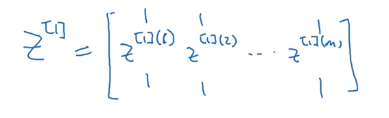
把 a [ 1 ] a^{[1]} a[1]堆叠起来就得到了 A [ 1 ] A^{[1]} A[1]: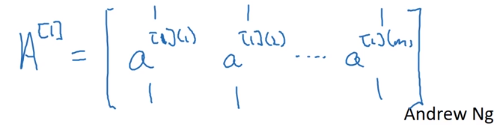
Z [ 2 ] Z^{[2]} Z[2]和 A [ 2 ] A^{[2]} A[2]也是一样的。
这些矩阵中列代表的是不同的样本,行就代表了网络中不同的节点。
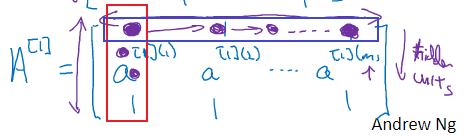
比如上面红框框出来的就是第一个样本第一层网络( A [ 1 ] A^{[1]} A[1]就说明是都是和第一层网络,也就是第一个隐藏层相关的)中所有神经元(节点)的输出。
而蓝框代表是这个 m m m个样本第一层网络中第一个神经元的输出。
下节给出向量化实现的解释。
向量化实现的解释
我们先对几个样本手动计算出正向传播。
假设这里我们计算出了3个样本的 z [ 1 ] z^{[1]} z[1]值,为了推导简单,我们先不考虑 b [ 1 ] b^{[1]} b[1],令它为零。
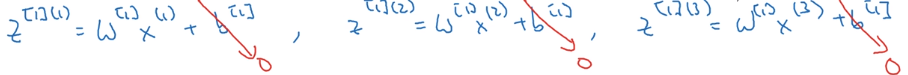
W [ 1 ] W^{[1]} W[1]是个矩阵,它与每个样本相乘得到一个向量。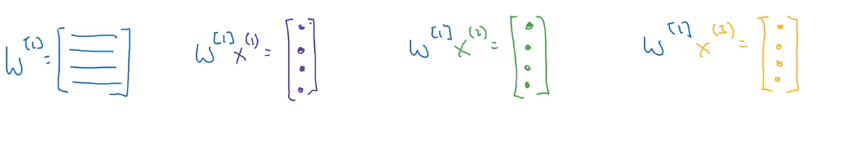
我们知道 X X X是这样表示的,这里用不同的样色代表不同的样本,和上面的图是一一对应的。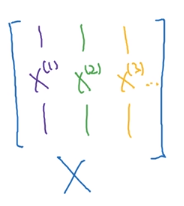
把 W [ 1 ] W^{[1]} W[1]乘以 X X X就得到了一个矩阵,这个矩阵里面的列就是每个样本与 W [ 1 ] W^{[1]} W[1]相乘的结果。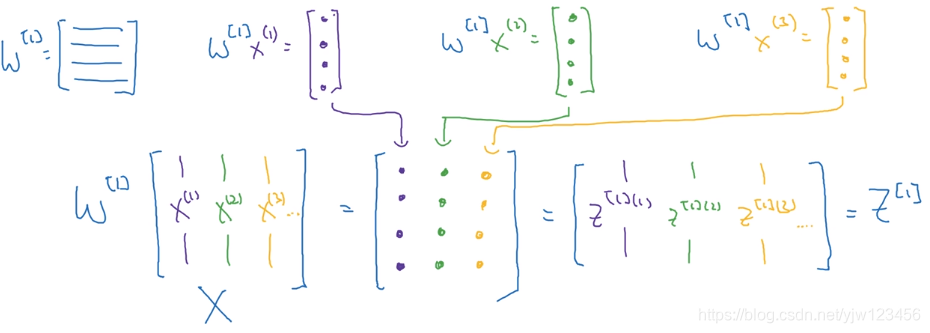
我们知道,这个矩阵里的值可以表示为 z [ 1 ] ( 1 ) , z [ 1 ] ( 1 ) , z [ 1 ] ( 3 ) ⋯ z^{[1](1)},z^{[1](1)},z^{[1](3)}\cdots z[1](1),z[1](1),z[1](3)⋯ ,我们用 Z [ 1 ] Z^{[1]} Z[1]表示这个矩阵。
还记得上面我们忽略了的 b [ 1 ] b^{[1]} b[1]没,因为它是一个列向量,我们可以把它们加回来(得益于python的广播,我们的代码可以很简单),得到更加完整的 Z [ 1 ] Z^{[1]} Z[1]表达:
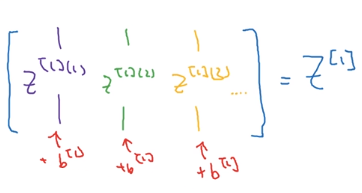
上面就说明了为什么 Z [ 1 ] = W [ 1 ] X + b [ 1 ] Z^{[1]} = W^{[1]} X + b^{[1]} Z[1]=W[1]X+b[1]
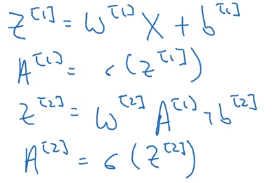
实际上,其他步骤也可以使用非常类似的逻辑,只要我们将输入按列向量堆叠,那么在方差运算后,我们就能得到按列向量堆叠的输出。
值得指出的是,我们知道 x x x可以表示为 a [ 0 ] a^{[0]} a[0],那么 X X X也可以表示为 A [ 0 ] A^{[0]} A[0],所以上面的式子具有一定的对称性。
这样我们就知道了神经网络的不同层中每一步做的都是一样的,只是同样的计算不停的重复而已。
这就是多个样本向量化的解释,上面我们一直用sigmoid函数作为激活函数,实际上这不是最好的选择,下节就来分析这一点。
激活函数
当我们构建神经网络的时候,我们可以选择隐藏层的激活函数和输出单元的激活函数。我们一直用sigmoid函数作为激活函数,实际上这不是最好的选择。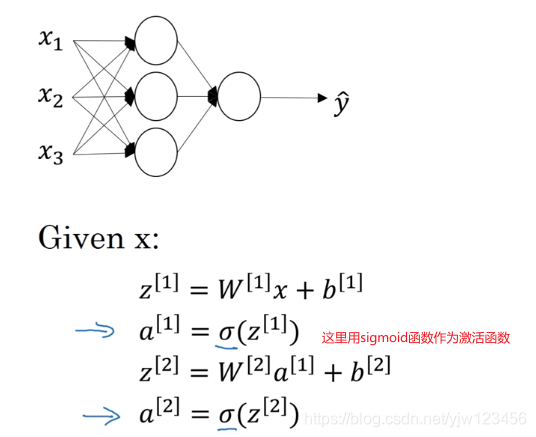
我们先看一下其他选择,实际上我们可以选择不同的激活函数,一般都是非线性函数。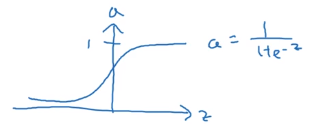
sigmoid函数图像是上面这样的,它取值范围是 [ 0 , 1 ] [0,1] [0,1],下面看一个更好的函数。
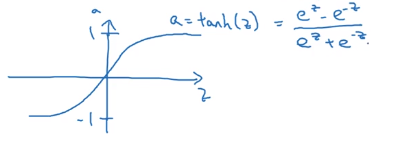
它的图像是这样的,这是tanh函数,截图中可能不太清晰,下面我再写一遍公式:
tanh ( z ) = e z − e − z e z + e − z \tanh (z) = \frac{e^z - e^{-z}}{e^z + e^{-z}} tanh(z)=ez+e−zez−e−z
这个函数穿过零点,取值范围是 [ − 1 , 1 ] [-1,1] [−1,1]。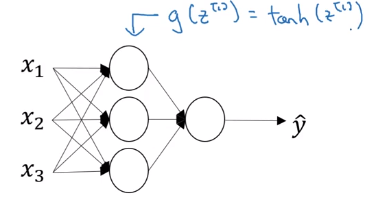
如果我们把激活函数改成tanh函数,几乎总比sigmoid函数效果要好。因为输出在 [ − 1 , 1 ] [-1,1] [−1,1]之间,输出的均值更接近于 0 0 0,因为你可能需要平移所有的数据,让它们的均值为零。使用tanh函数就有这种类似数据中心化的效果。这样会让下一层的学习更加方便一些。这部分内容第二节课中会讲到,现在不懂也没关系。
现在我们可以把所有的sigmoid函数都改成tanh函数了,除了输出层。因为实际值是0或1,因此我们希望 y ^ \hat y y^也是0或1更合理。所以在这种二分类的情况中,依然会使用sigmoid函数作为输出层的激活函数。
所以可以看到,不同层的激活函数可以不同。可能就需要 g [ 1 ] , g [ 2 ] g^{[1]},g^{[2]} g[1],g[2]来表示两个层的激活函数的不同了。
其实sigmoid函数和tanh函数都有一个缺点,就是梯度消失问题。如果输出值很大或者很小,那么这两个函数的导数很可能就是0。
这样有什么问题呢,比如你的某个特征的输入很大,假设是5000,经过第一层的sigmoid函数,被压缩到了1,再多经过几层,可能得到的输出就成了0了,导致你不管怎么加大这个特征的输入都不会影响到最终的输出。
所以在神经网络中比较常用的激活函数其实是ReLU函数,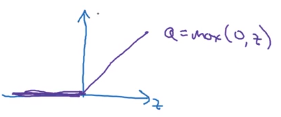
r e l u ( z ) = max ( 0 , z ) relu(z) = \max(0,z) relu(z)=max(0,z)
在选择激活函数时有一些经验法则,如果输出值是0和1,那么就用sigmoid函数作为输出层的激活函数,其他层就用ReLU函数。
但ReLU函数也有一个缺点,就是当 z z z为负数时,导数等于零。因此有人就提出了Leaky ReLU,这通常比ReLU激活函数更好,但实际上使用频率不高,Leaky ReLU的图像是这样的。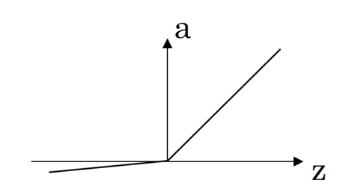
它的式子是这样的: m a x ( 0.01 z , z ) max(0.01z,z) max(0.01z,z),就不会有导数为零的问题了。当然你也可以取其他数字,不取0.01。
为什么需要(非线性)激活函数
可能有人会问,为什么需要激活函数,不能直接去掉吗。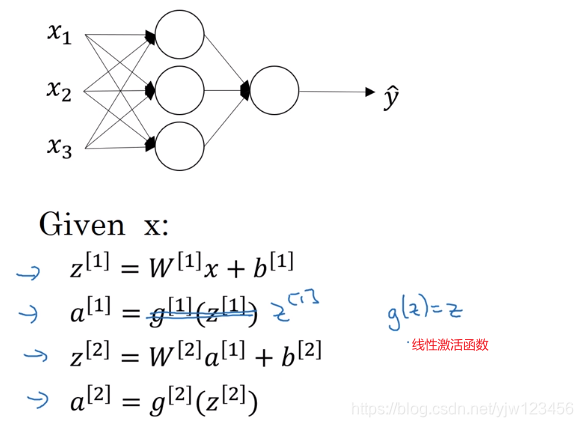
比如我们把之前介绍的激活函数直接替换为 z [ 1 ] z^{[1]} z[1],也就是没有激活函数。
如果没有激活函数(或者使用线性激活函数),那么不管有多少层的网络,我们的网络都只是特征 x x x的线性组合而已。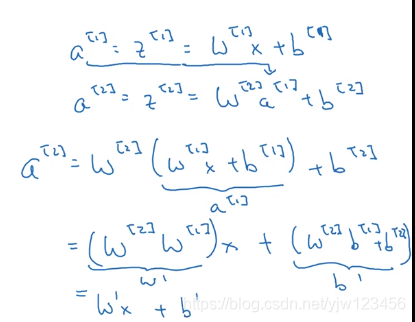
只有一种情况下输出层(隐藏层还是要使用非线性函数)可以使用线性激活函数,那就是要解决回归问题。
好了,下面我们要讨论的是神经网络的梯度下降法, 但是在这之前,我们需要知道激活函数的导数。
激活函数的导数
我们已经知道了sigmoid函数的导数 σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) \sigma ^\prime(z) = \sigma(z)(1-\sigma(z)) σ′(z)=σ(z)(1−σ(z))(在上篇文章中有详细的证明。)
我们重点来看下tanh函数的导数。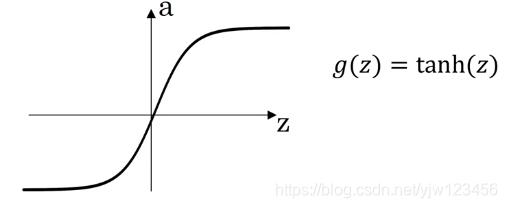
g ( z ) = t a n h ( z ) = e z − e − z e z + e − z g(z) = tanh(z) = \frac {e^z - e^{-z}} {e^z + e^{-z}} g(z)=tanh(z)=ez+e−zez−e−z
需用用到导数的四则运算,从人工智能数学基础之高等数学中截取部分出来:
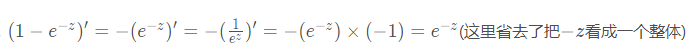
在上篇文章中,我们知道 ( 1 − e − z ) ′ = e − z (1-e^{-z})^\prime = e^{-z} (1−e−z)′=e−z,那么 ( e − z ) ′ = − e − z (e^{-z})^\prime = - e^{-z} (e−z)′=−e−z
( e z − e − z ) ′ = e z + e − z (e^z - e^{-z})^\prime =e^z + e^{-z} (ez−e−z)′=ez+e−z
( e z + e − z ) ′ = e z − e − z (e^z + e^{-z})^\prime =e^z - e^{-z} (ez+e−z)′=ez−e−z
上面这些在下面求导的时候可以直接代入:
g ′ ( z ) = ( e z − e − z e z + e − z ) ′ = ( e z − e − z ) ′ ( e z + e − z ) − ( e z − e − z ) ( e z + e − z ) ′ ( e z + e − z ) 2 = ( e z + e − z ) 2 − ( e z − e − z ) 2 ( e z + e − z ) 2 = 1 − ( e z − e − z ) 2 ( e z + e − z ) 2 = 1 − ( e z − e − z e z + e − z ) 2 = 1 − g ( z ) 2 \begin{aligned} g^\prime(z) &=\left( \frac {e^z - e^{-z}} {e^z + e^{-z}} \right)^{\prime} \\ &= \frac{(e^z - e^{-z})^\prime (e^z + e^{-z}) - (e^z - e^{-z})(e^z + e^{-z})^\prime}{(e^z + e^{-z})^2} \\ &= \frac{(e^z + e^{-z})^2 - (e^z - e^{-z})^2}{(e^z + e^{-z})^2} \\ &= 1 - \frac{(e^z - e^{-z})^2}{(e^z + e^{-z})^2} \\ &= 1- \left(\frac{e^z - e^{-z}}{e^z + e^{-z}} \right)^2 \\ &= 1 - g(z)^2 \end{aligned} g′(z)=(ez+e−zez−e−z)′=(ez+e−z)2(ez−e−z)′(ez+e−z)−(ez−e−z)(ez+e−z)′=(ez+e−z)2(ez+e−z)2−(ez−e−z)2=1−(ez+e−z)2(ez−e−z)2=1−(ez+e−zez−e−z)2=1−g(z)2
也就是说
tanh ′ ( x ) = 1 − tanh ( x ) 2 \tanh ^\prime(x) = 1 - \tanh (x)^2 tanh′(x)=1−tanh(x)2
最后看下最简单的ReLU函数的导数。
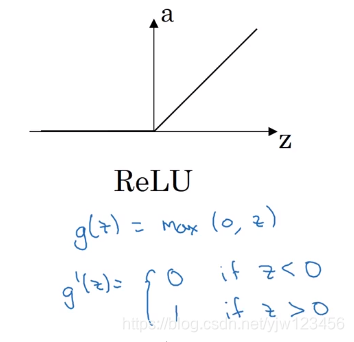
很简单,当 z < 0 z <0 z<0时,导数为 0 0 0;当 z > 0 z > 0 z>0时,导数为 1 1 1。
最后看一下Leaky ReLU的导数: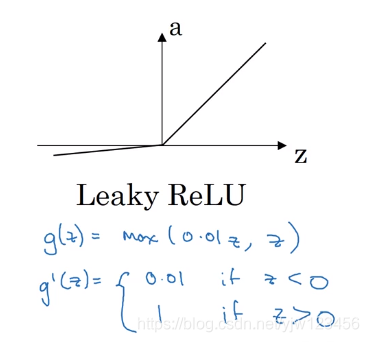
下面我们就可以开始了解审计网络的梯度下降法了。
神经网络的梯度下降法
本小节一起来学习下神经网络的梯度下降法,或者说反向传播法。
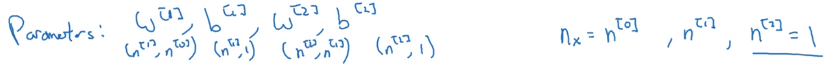
我们有 n [ 0 ] n^{[0]} n[0]个输入特征, n [ 1 ] n^{[1]} n[1]个隐藏单元, n [ 2 ] n^{[2]} n[2]个输出单元。
参数 W [ 1 ] W^{[1]} W[1]就是 ( n [ 1 ] × n [ 0 ] ) (n^{[1]} \times n^{[0]}) (n[1]×n[0])(第一层的神经元数 乘以 第一层的输入数),
b [ 1 ] b^{[1]} b[1]就是 ( n [ 1 ] × 1 ) (n^{[1]} \times 1) (n[1]×1)(第一层的神经元数 乘以 1),因为每个神经元相当于一个逻辑回归,只有一个偏差。
参数 W [ 2 ] W^{[2]} W[2]就是 ( n [ 2 ] × n [ 1 ] ) (n^{[2]} \times n^{[1]}) (n[2]×n[1])(第二层的神经元数 乘以 第二层的输入数),
b [ 2 ] b^{[2]} b[2]就是 ( n [ 2 ] × 1 ) (n^{[2]} \times 1) (n[2]×1)(第二层的神经元数 乘以 1)
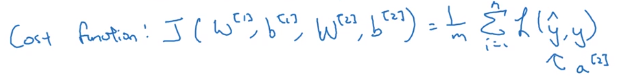
假设我们在做二分类,我们的成本函数就会是上面这样,这和逻辑回归的完全一样。
所以要训练这些参数,我们需要梯度下降。在训练神经网络时,参数的初始化很重要,需要随机初始化,不能初始化为零。
神经网络的梯度下降法是这样的:
我们已经知道了如何计算出预测值(神经网络的输出)。
现在的问题是如何计算这些偏导数。
我们先总结一下正向传播的过程。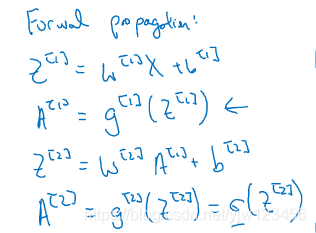
在上一篇文章中,我们已经知道了如何求逻辑回归的梯度:
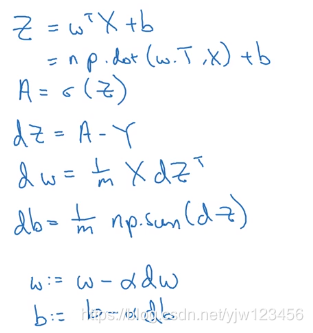
下面我们来计算神经网络的梯度,就是反向传播的步骤,这里先贴出结果,证明可以见下一小节。

首先是上面这样的,从输出开始计算出偏导,上面就是计算输出层中参数的偏导,这里和逻辑回归中的很像,下面就来看下如何计算输出层的前一层,也就是隐藏层的偏导。

所以这就是反向传播的过程,有六个方程,而正向传播只有两个。下面就来解释为什么是这样的。
直观理解反向传播
我们还是通过计算图的方式来告诉大家上节反向传播中方程是如何推出来的。

当我们讨论逻辑回归的时候(上篇文章),我们有这样一个计算图。我们用它理解了逻辑回归的正向传播和反向传播。
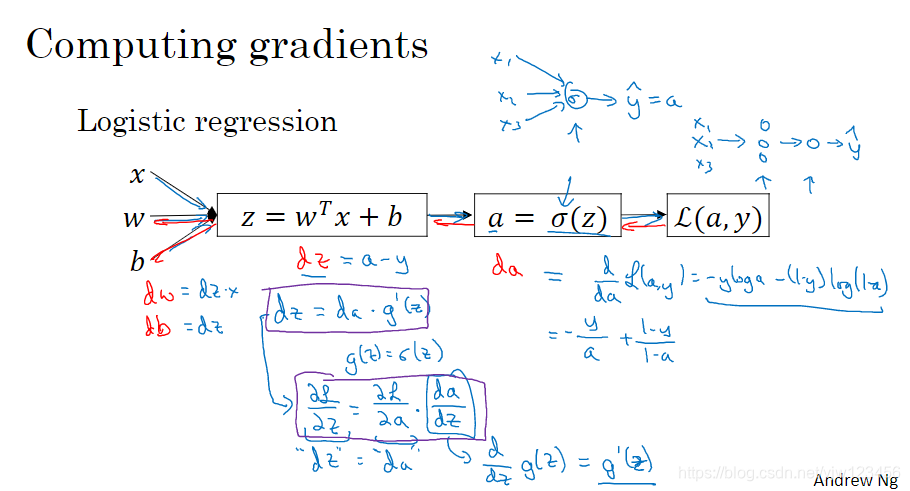
我们计算神经网络的反向传播时,做的计算和上面很像。
但是因为我们的神经网络有两层,所以会计算两次。先计算输出层,再反过来计算隐藏层。
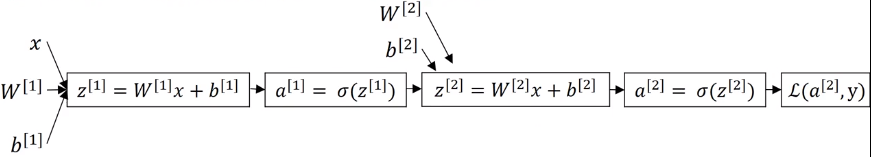
我们这个双层神经网络的计算图如上。
从左到右就是正向传播。

而反向传播的顺序是相反的,先计算出 d a [ 2 ] da^{[2]} da[2],再是 d z [ 2 ] dz^{[2]} dz[2],然后是 z [ 2 ] z^{[2]} z[2]的参数 d W [ 2 ] dW^{[2]} dW[2]和 d b [ 2 ] db^{[2]} db[2];
接着计算 d a [ 1 ] da^{[1]} da[1], d z [ 1 ] dz^{[1]} dz[1],最终可以计算 d W [ 1 ] , d b [ 1 ] dW^{[1]},db^{[1]} dW[1],db[1]。
和上篇文章中一样,我们先计算出 d a [ 2 ] da^{[2]} da[2],在计算出 d z [ 2 ] dz^{[2]} dz[2],下面贴出上篇文章的计算过程: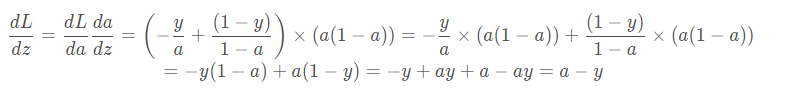
其实是一样的,符号不同而已,代入就得到了 d z [ 2 ] = a [ 2 ] − y dz^{[2]} = a^{[2]} - y dz[2]=a[2]−y。
然后
d z [ 2 ] d W [ 2 ] = d ( W [ 2 ] x + b [ 2 ] ) d W [ 2 ] = x \frac{dz^{[2]}}{dW^{[2]}} = \frac{d(W^{[2]} x + b^{[2]})}{dW^{[2]}} = x dW[2]dz[2]=dW[2]d(W[2]x+b[2])=x
就可以得到:
d L W [ 2 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] d z [ 2 ] d W [ 2 ] = d z [ 2 ] d z [ 2 ] d W [ 2 ] = ( a [ 2 ] − y ) × x \frac{dL}{W^{[2]}} = \frac{dL}{da^{[2]}} \frac{da^{[2]}}{dz^{[2]}} \frac{dz^{[2]}}{dW^{[2]}} =dz^{[2]} \frac{dz^{[2]}}{dW^{[2]}} = (a^{[2]}-y) \times x W[2]dL=da[2]dLdz[2]da[2]dW[2]dz[2]=dz[2]dW[2]dz[2]=(a[2]−y)×x
然后
d z [ 2 ] d b [ 2 ] = d ( W [ 2 ] x + b [ 2 ] ) d b [ 2 ] = 1 \frac{dz^{[2]}}{db^{[2]}} = \frac{d(W^{[2]} x + b^{[2]})}{db^{[2]}} = 1 db[2]dz[2]=db[2]d(W[2]x+b[2])=1
同理
d L b [ 2 ] = d z [ 2 ] d z [ 2 ] d b [ 2 ] = d z [ 2 ] = a [ 2 ] − y \frac{dL}{b^{[2]}} = dz^{[2]} \frac{dz^{[2]}}{db^{[2]}} =dz^{[2]} = a^{[2]} - y b[2]dL=dz[2]db[2]dz[2]=dz[2]=a[2]−y
然后计算 d a [ 1 ] da^{[1]} da[1]
d a [ 1 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] d z [ 2 ] d a [ 1 ] da^{[1]} = \frac{dL}{da^{[2]}} \frac{da^{[2]}}{dz^{[2]}} \frac{dz^{[2]}}{da^{[1]}} da[1]=da[2]dLdz[2]da[2]da[1]dz[2]
因此,我们需要先计算 d z [ 2 ] d a [ 1 ] \frac{dz^{[2]}}{da^{[1]}} da[1]dz[2],因为 a [ 1 ] a^{[1]} a[1]是代入到 z [ 2 ] z^{[2]} z[2]中的 x x x的,这里也就是 x = a [ 1 ] x = a^{[1]} x=a[1]:
d z [ 2 ] d a [ 1 ] = d ( W [ 2 ] a [ 1 ] + b [ 2 ] ) d a [ 1 ] = W [ 2 ] \frac{dz^{[2]}}{da^{[1]}} = \frac{d(W^{[2]} a^{[1]} + b^{[2]})}{da^{[1]}} = W^{[2]} da[1]dz[2]=da[1]d(W[2]a[1]+b[2])=W[2]
这样,我们就可以得到:
d a [ 1 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] d z [ 2 ] d a [ 1 ] = ( a [ 2 ] − y ) W [ 2 ] da^{[1]} = \frac{dL}{da^{[2]}} \frac{da^{[2]}}{dz^{[2]}} \frac{dz^{[2]}}{da^{[1]}} = (a^{[2]} - y)W^{[2]} da[1]=da[2]dLdz[2]da[2]da[1]dz[2]=(a[2]−y)W[2]
继续计算 d z [ 1 ] dz^{[1]} dz[1]
d z [ 1 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] d z [ 2 ] d a [ 1 ] d a [ 1 ] d z [ 1 ] = dz^{[1]} = \frac{dL}{da^{[2]}} \frac{da^{[2]}}{dz^{[2]}} \frac{dz^{[2]}}{da^{[1]}} \frac{da^{[1]}}{dz^{[1]}} = dz[1]=da[2]dLdz[2]da[2]da[1]dz[2]dz[1]da[1]=
我们还要先要计算出 d a [ 1 ] d z [ 1 ] \frac{da^{[1]}}{dz^{[1]}} dz[1]da[1]
d a [ 1 ] d z [ 1 ] = g ′ ( z [ 1 ] ) = d σ ( z [ 1 ] ) d z [ 1 ] = a [ 1 ] ( 1 − a [ 1 ] ) \frac{da^{[1]}}{dz^{[1]}} = g^\prime(z^{[1]}) = \frac{d \sigma(z^{[1]})}{d z^{[1]}} = a^{[1]}(1 - a^{[1]}) dz[1]da[1]=g′(z[1])=dz[1]dσ(z[1])=a[1](1−a[1])
所以
d z [ 1 ] = d L d a [ 2 ] d a [ 2 ] d z [ 2 ] d z [ 2 ] d a [ 1 ] d a [ 1 ] d z [ 1 ] = ( a [ 2 ] − y ) W [ 2 ] ∗ a [ 1 ] ( 1 − a [ 1 ] ) = d z [ 2 ] W [ 2 ] ∗ g ′ ( z [ 1 ] ) dz^{[1]} = \frac{dL}{da^{[2]}} \frac{da^{[2]}}{dz^{[2]}} \frac{dz^{[2]}}{da^{[1]}} \frac{da^{[1]}}{dz^{[1]}} = (a^{[2]} - y)W^{[2]} * a^{[1]}(1 - a^{[1]}) = dz^{[2]} W^{[2]} * g^\prime(z^{[1]}) dz[1]=da[2]dLdz[2]da[2]da[1]dz[2]dz[1]da[1]=(a[2]−y)W[2]∗a[1](1−a[1])=dz[2]W[2]∗g′(z[1])
(最后那个等式是改成上节中梯度下降伪代码中的样子。)
我们先来看下维度,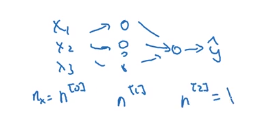
我们是一个这样的网络,输出只有一个维度。
W [ 2 ] W^{[2]} W[2]是 ( n [ 2 ] × n [ 1 ] ) (n^{[2]} \times n ^{[1]}) (n[2]×n[1])
z [ 2 ] , d z [ 2 ] z^{[2]},dz^{[2]} z[2],dz[2]它们的维度是一样的,都是 ( n [ 2 ] × 1 ) (n^{[2]} \times 1) (n[2]×1),做二分类时,就是 ( 1 × 1 ) (1 \times 1) (1×1)。
然后 z [ 1 ] , d z [ 1 ] z^{[1]},dz^{[1]} z[1],dz[1]都是 ( n [ 1 ] × 1 ) (n^{[1]} \times 1) (n[1]×1)
为了让维度匹配,我们让 d z [ 1 ] = w [ 2 ] T d z [ 2 ] dz^{[1]} = w^{[2]T} dz^{[2]} dz[1]=w[2]Tdz[2] 维度是这样的: ( n [ 1 ] × n [ 2 ) × ( n [ 2 ] × 1 ) = ( n [ 1 ] × 1 ) (n^{[1]} \times n ^{[2}) \times (n^{[2]} \times 1) = (n^{[1]} \times 1) (n[1]×n[2)×(n[2]×1)=(n[1]×1)
又 z [ 1 ] , g ′ ( z [ 1 ] ) z^{[1]},g^\prime(z^{[1]}) z[1],g′(z[1])的维度也是 ( n [ 1 ] × 1 ) (n^{[1]} \times 1) (n[1]×1)。
所以 d z [ 1 ] = w [ 2 ] T d z [ 2 ] ∗ g ′ ( z [ 1 ] ) dz^{[1]} = w^{[2]T} dz^{[2]} * g^\prime(z^{[1]}) dz[1]=w[2]Tdz[2]∗g′(z[1])
上面的 ∗ * ∗表示逐元素相乘。
确保矩阵的维度相匹配很重要。
最后就剩下 d W [ 1 ] , d b [ 1 ] dW^{[1]},db^{[1]} dW[1],db[1]了。
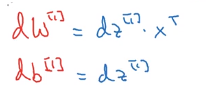
这个其实和计算 d W [ 2 ] , d b [ 2 ] dW^{[2]},db^{[2]} dW[2],db[2]的过程是一样的,这里就不写出来了,感兴趣的可以自己推下。
这样,我们就证明了下面这些方程的成立: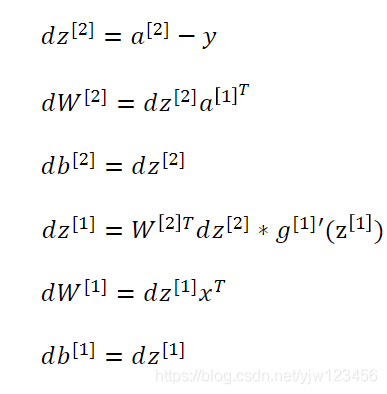
现在我们得到了上面的公式,我们就可以写出计算反向传播的代码了,如果有多个样本的话,我们也可以向量化。

上图右边就是反向传播的向量化写法。和逻辑回归梯度下降算法向量化的过程类似。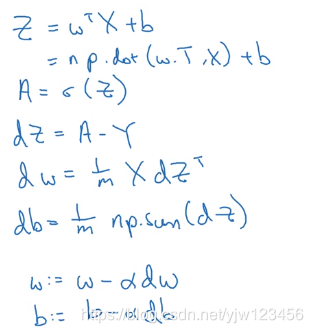
此时有多个样本,因此最终得到的 d W [ 2 ] d^W{[2]} dW[2]和 d b [ 2 ] db^{[2]} db[2]要除以样本的数量,用均值作为更新的量。
求 d b [ 2 ] db^{[2]} db[2]的时候axis=1意思是沿着列的方向求和,也就是计算所有列(样本)的和。
对照左边可以很快写成向量化的形式,注意维度相匹配即可。
随机初始化
在上文中有说过,初始化神经网络的参数 W W W时,一般不会初始化为零。
为什么呢?
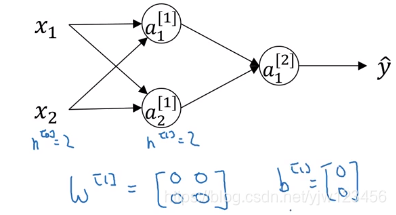
假设有个这样的神经网络,然后参数都初始化为零。
这样不管输入是什么,两个隐藏单元的激活值完全一样。当做反向传播时, d z 1 [ 1 ] dz^{[1]}_1 dz1[1]和 d z 2 [ 1 ] dz^{[1]}_2 dz2[1]也是一样的。
如果 W W W初始值为零的话,那么这两个隐藏层的神经元完全一样了,这样会导致每次训练迭代后,两个隐藏单元仍然在计算完全相同的函数。
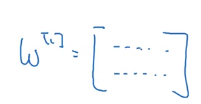
W [ 1 ] W^{[1]} W[1]在更新后,我们会发现它的两行是完全一样的。因此这这种情况下,有多个隐藏单元是没有意义的。
对于隐藏层有更多的单元的网络也是一样的,只要 W W W初始为零,它们都是的一样的。
解决方法就是随机初始化参数。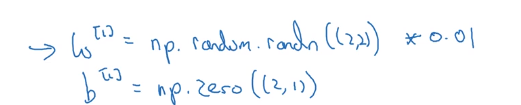
这里 b b b被证明是可以初始化为零的。
上面 W [ 1 ] W^{[1]} W[1]初始的随机值后面乘以 0.01 0.01 0.01是想让权重初始化成非常小的随机值。
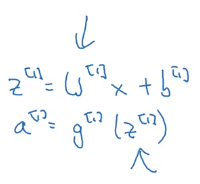
因为当使用sigmoid或tanh激活函数时,当权重过大,会导致 Z Z Z的值过大(或过小),
这样导致激活值可能会落在激活函数的平缓部分(上图箭头指向的位置),导致导数非常小,就会使得梯度下降算法非常慢。
实际上有比上面的 0.01 0.01 0.01更好的常数,这一点第二节课会谈到。
参考
(推荐网易云课堂,可以免费看并且还有课堂笔记。)
1. 吴恩达深度学习
更多推荐
 已为社区贡献38条内容
已为社区贡献38条内容

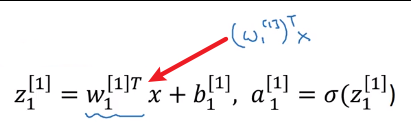









所有评论(0)