基于python实现了三方演化博弈，定义replicator_dynamics函数生成动态方程，compute_jacobian计算雅可比矩阵，analyze_stability进行更全面的稳定性分析，支持符号和数值两种方式，dynamic_simulation处理数值仿真，以及可视化函数。

# -*- coding: utf-8 -*-
"""
三方演化博弈完整实现 - 修复稳定性分析版本
包含：符号计算、动态仿真、稳定性分析、三维可视化
"""
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt

# ================ 修复中文显示 ================
plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置黑体
plt.rcParams['axes.unicode_minus'] = False    # 修复负号显示
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D

# ================== 符号定义 ==================
x, y, z = sp.symbols('x y z')  # 决策变量
Rp, Cph, Cpl, Cp, Bt, Fp, Mp, Ct, Ft, Mt, Cg, Tg = sp.symbols(
    'Rp Cph Cpl Cp Bt Fp Mp Ct Ft Mt Cg Tg'
)


# ================== 模型核心 ==================
def replicator_dynamics():
    """三方复制动态方程"""
    dx = x * (1 - x) * (Cph - Cpl - Cp - Bt - y * (Rp - Bt) - z * (Fp + Mp))
    dy = y * (1 - y) * ((1 - x) * (Bt - Mt) - (Ft + Mt) * z - Ct)
    dz = z * (1 - z) * (Cg - Fp - Ft - Tg + (Mp + Fp + Tg) * x + (Mt + Ft + Tg) * y - Tg * x * y)
    return [dx, dy, dz]


def compute_jacobian():
    """计算雅可比矩阵（带参数保留）"""
    eqs = replicator_dynamics()
    return sp.Matrix([[sp.simplify(sp.diff(eq, var)) for var in [x, y, z]] for eq in eqs])


def analyze_stability(jacobian, params=None):
    """
    增强版稳定性分析
    :param jacobian: 雅可比矩阵
    :param params: 参数字典（可选，用于数值计算）
    :return: 稳定性分析结果字典
    """
    equilibrium_points = [
        (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1),
        (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)
    ]

    # 参数替换
    subs_dict = {}
    if params:
        subs_dict = {
            Rp: params['Rp'], Cph: params['Cph'], Cpl: params['Cpl'],
            Cp: params['Cp'], Bt: params['Bt'], Fp: params['Fp'],
            Mp: params['Mp'], Ct: params['Ct'], Ft: params['Ft'],
            Mt: params['Mt'], Cg: params['Cg'], Tg: params['Tg']
        }

    results = {}
    for point in equilibrium_points:
        # 代入均衡点
        J = jacobian.subs({x: point[0], y: point[1], z: point[2]})

        # 参数替换
        if subs_dict:
            J = J.subs(subs_dict)

        try:
            # 尝试数值计算
            J_np = np.array(J.tolist(), dtype=np.float64)
            eigvals = np.linalg.eigvals(J_np)
            stable = all(np.real(eigvals) < 0)
            results[point] = {
                'type': 'numerical',
                'eigenvalues': eigvals,
                'stable': stable
            }
        except TypeError:
            # 符号分析处理
            eig_dict = J.eigenvals()
            eig_list = []
            for val, count in eig_dict.items():
                eig_list.extend([val] * count)

            conditions = [sp.re(val) < 0 for val in eig_list]
            results[point] = {
                'type': 'symbolic',
                'eigenvalues': eig_list,
                'conditions': conditions
            }

    return results


# ================== 数值仿真 ==================
def dynamic_simulation(ic, t, params):
    """动态仿真函数"""
    # 参数替换字典
    subs_dict = {
        Rp: params['Rp'], Cph: params['Cph'], Cpl: params['Cpl'],
        Cp: params['Cp'], Bt: params['Bt'], Fp: params['Fp'],
        Mp: params['Mp'], Ct: params['Ct'], Ft: params['Ft'],
        Mt: params['Mt'], Cg: params['Cg'], Tg: params['Tg']
    }

    # 转换为数值函数
    dx, dy, dz = replicator_dynamics()
    dx_num = sp.lambdify((x, y, z), dx.subs(subs_dict), 'numpy')
    dy_num = sp.lambdify((x, y, z), dy.subs(subs_dict), 'numpy')
    dz_num = sp.lambdify((x, y, z), dz.subs(subs_dict), 'numpy')

    def system(state, t):
        return [
            dx_num(*state),
            dy_num(*state),
            dz_num(*state)
        ]

    return odeint(system, ic, t)


# ================== 可视化 ==================
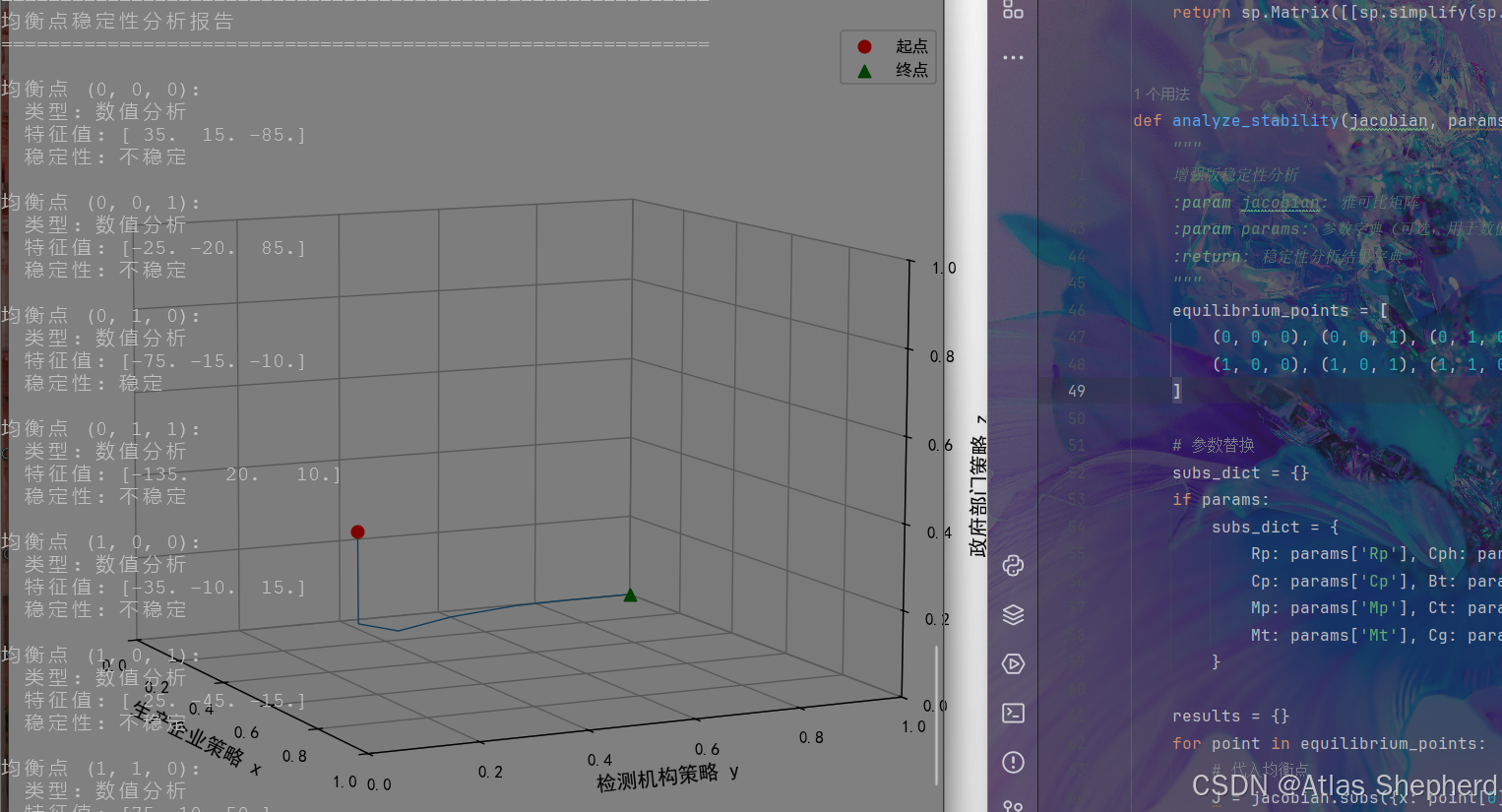
def plot_3d_trajectory(data, title="三方博弈演化轨迹"):
    """三维演化轨迹可视化"""
    fig = plt.figure(figsize=(12, 8))
    ax = fig.add_subplot(111, projection='3d')

    ax.plot(data[:, 0], data[:, 1], data[:, 2], lw=0.8)
    ax.scatter(data[0, 0], data[0, 1], data[0, 2], c='r', marker='o', s=50, label='起点')
    ax.scatter(data[-1, 0], data[-1, 1], data[-1, 2], c='g', marker='^', s=50, label='终点')

    ax.set_xlim(0, 1)
    ax.set_ylim(0, 1)
    ax.set_zlim(0, 1)
    ax.set_xlabel('生产企业策略 x', fontsize=12)
    ax.set_ylabel('检测机构策略 y', fontsize=12)
    ax.set_zlabel('政府部门策略 z', fontsize=12)
    ax.view_init(elev=25, azim=-45)
    plt.title(title, fontsize=14, pad=20)
    plt.legend()
    plt.tight_layout()
    plt.show()


def print_stability(results):
    """格式化输出稳定性分析结果"""
    print("\n" + "=" * 60)
    print("均衡点稳定性分析报告")
    print("=" * 60)

    for point, info in results.items():
        print(f"\n均衡点 {point}:")
        if info['type'] == 'numerical':
            print(f"  类型: 数值分析")
            print(f"  特征值: {info['eigenvalues'].round(4)}")
            print(f"  稳定性: {'稳定' if info['stable'] else '不稳定'}")
        else:
            print(f"  类型: 符号分析")
            print("  特征值条件:")
            for cond in info['conditions']:
                print(f"  → {sp.pretty(cond, use_unicode=True)}")


# ================== 示例执行 ==================
if __name__ == "__main__":
    # 参数设置
    params = {
        'Rp': 150, 'Cph': 85, 'Cpl': 0, 'Cp': 10,
        'Bt': 40, 'Fp': 40, 'Mp': 20, 'Ct': 10,
        'Ft': 20, 'Mt': 15, 'Cg': 15, 'Tg': 40
    }

    # 计算雅可比矩阵
    jac = compute_jacobian()

    # 带参数的稳定性分析
    stability_results = analyze_stability(jac, params=params)
    print_stability(stability_results)

    # 动态仿真
    t = np.linspace(0, 50, 1000)
    trajectory = dynamic_simulation(
        ic=(0.3, 0.3, 0.3),
        t=t,
        params=params
    )

    # 可视化
    plot_3d_trajectory(trajectory, "基准参数下的演化轨迹")