目录

一、傅里叶分析

1. 核心思想与数学基础

 2. 快速傅里叶变换（FFT）

3. 应用场景与局限性

二、小波分析

1. 核心思想与数学基础

2. 小波变换类型

3. 代码实现

离散小波变换（DWT）去噪示例

连续小波变换（CWT）时频分析

4. 应用场景与优势

三、傅里叶 vs. 小波对比

四、在故障诊断中的联合应用案例

案例：轴承故障诊断

五、工程挑战与解决方案

1. 噪声干扰

2. 计算效率优化

3. 实际数据适配

六、前沿技术融合

1. 深度学习与小波结合

2. 数字孪生中的实时分析

总结

---

一、傅里叶分析

1. 核心思想与数学基础

• 基本目标：将信号分解为不同频率的正弦/余弦波叠加，揭示信号的频域特征。

• 数学表达：
  连续傅里叶变换（CFT）：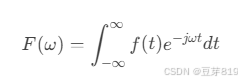

  

  离散傅里叶变换（DFT）：

     

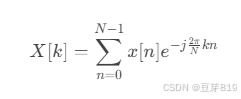
• 关键概念：

  • 频谱：信号在频域的幅度和相位分布。

  • 采样定理：采样频率需大于信号最高频率的2倍（Nyquist定理）。

 2. 快速傅里叶变换（FFT）

• 原理：利用分治思想加速DFT计算，复杂度从𝑂(𝑁2) 降至 𝑂(𝑁log⁡𝑁)。

• 代码实现（Python）：

import numpy as np
from scipy.fft import fft
import matplotlib.pyplot as plt

# 生成信号（含10Hz和20Hz正弦波）
fs = 1000  # 采样率1000Hz
t = np.linspace(0, 1, fs)
signal = np.sin(2*np.pi*10*t) + 0.5*np.sin(2*np.pi*20*t)

# FFT变换
fft_result = fft(signal)[:len(signal)//2]
frequencies = np.linspace(0, fs/2, len(fft_result))

# 绘制频谱图
plt.plot(frequencies, np.abs(fft_result))
plt.xlabel('Frequency (Hz)'), plt.ylabel('Amplitude')
plt.title('FFT Spectrum')
plt.show()

输出：频谱图中将显示10Hz和20Hz的峰值。

如图所示

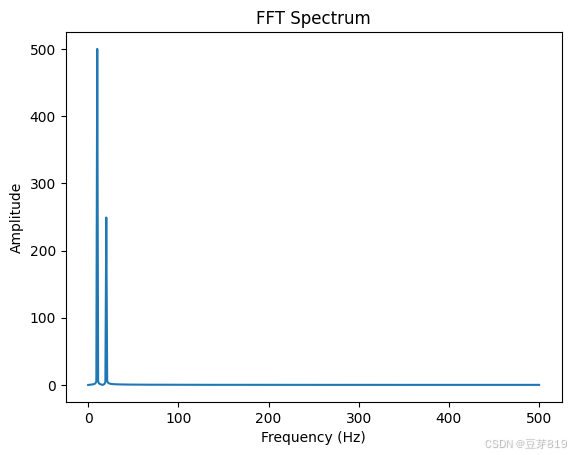
3. 应用场景与局限性

• 适用场景：

  • 稳态信号分析（如电机均匀磨损的振动信号）。

  • 频域特征提取（如轴承故障的特征频率识别）。

• 局限性：

  • 无法定位时间信息：无法回答“某个频率成分在何时出现”。

  • 对非平稳信号效果差：如冲击故障（瞬时高频）或时变信号。

二、小波分析

1. 核心思想与数学基础

• 基本目标：通过缩放和平移母小波函数，实现信号的时频联合分析。

• 数学表达：
  连续小波变换（CWT）：

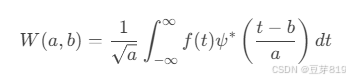
       离散小波变换（DWT）：通过滤波器组（低通+高通）实现多尺度分解。

• 关键概念：

  • 母小波（Mother Wavelet）：如Morlet、Daubechies（dbN）、Haar小波。

  • 尺度（Scale）与平移（Translation）：尺度控制频率，平移控制时间位置。

2. 小波变换类型

类型	特点	适用场景
连续小波变换	尺度和平移连续变化，计算量大	信号细节分析（如故障起始点定位）
离散小波变换	使用二进尺度和平移，计算高效	信号压缩、去噪
小波包分解	进一步分解高频分量，提供更精细的时频分辨率	非平稳信号特征提取

3. 代码实现

离散小波变换（DWT）去噪示例

import pywt
import numpy as np

# 生成含噪信号
t = np.linspace(0, 1, 1000)
clean_signal = np.sin(2*np.pi*5*t)
noise = 0.5*np.random.randn(1000)
noisy_signal = clean_signal + noise

# 小波分解与去噪
coeffs = pywt.wavedec(noisy_signal, 'db4', level=5)  # 5层分解
threshold = np.std(coeffs[-5]) * np.sqrt(2*np.log(len(noisy_signal)))  # 阈值计算
coeffs_thresh = [pywt.threshold(c, threshold, mode='soft') for c in coeffs]  # 软阈值处理
denoised_signal = pywt.waverec(coeffs_thresh, 'db4')  # 重构信号

# 绘制结果
plt.figure()
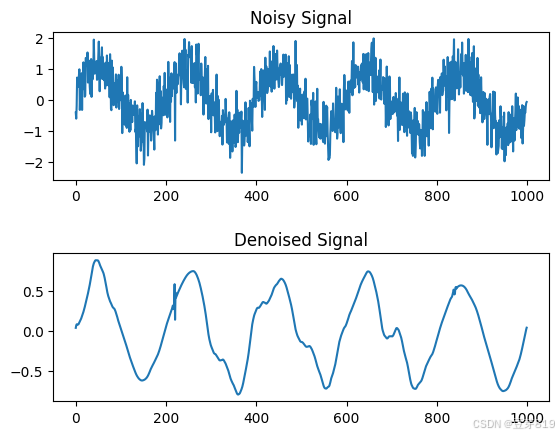
plt.subplot(211), plt.plot(noisy_signal), plt.title('Noisy Signal')
plt.subplot(212), plt.plot(denoised_signal), plt.title('Denoised Signal')
plt.show()

如图所示

连续小波变换（CWT）时频分析

import pywt
import matplotlib.pyplot as plt

# 生成冲击信号（瞬时高频）
t = np.linspace(0, 1, 1000)
signal = np.zeros(1000)
signal[400:450] = np.sin(2*np.pi*50*t[400:450])  # 50Hz短时脉冲

# CWT分析
scales = np.arange(1, 128)
coefficients, frequencies = pywt.cwt(signal, scales, 'morl', sampling_period=0.001)

# 绘制时频图
plt.imshow(np.abs(coefficients), extent=[0, 1, 1, 128], cmap='jet', aspect='auto')
plt.xlabel('Time (s)'), plt.ylabel('Scale')
plt.title('CWT Scalogram')
plt.colorbar()
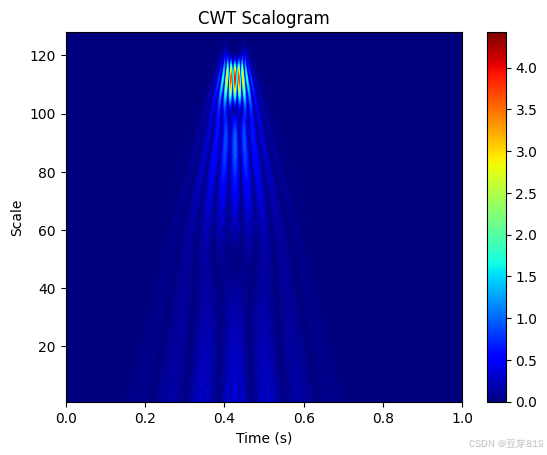
plt.show()

输出：时频图中可清晰看到50Hz成分在0.4-0.45秒出现。

如图所示

4. 应用场景与优势

• 适用场景：

  • 非平稳信号分析：如轴承冲击故障、刀具崩刃瞬态信号。

  • 图像处理：边缘检测（Haar小波）、图像压缩（JPEG2000标准）。

• 核心优势：

  • 时频局部化：同时提供时间和频率信息。

  • 多分辨率分析：通过不同尺度捕捉信号的粗细特征。

三、傅里叶 vs. 小波对比

特性	傅里叶分析	小波分析
时频分辨率	全局频率分辨率，无时间定位	自适应时频分辨率（高频短时，低频长时）
信号类型	稳态信号（频率成分不随时间变化）	非平稳信号（瞬时、突变、时变频率）
计算复杂度	FFT高效（𝑂(𝑁log⁡𝑁)）	DWT高效（𝑂(𝑁)），CWT较高（O(）
典型应用	频谱分析、滤波器设计	故障诊断、图像压缩、语音识别

四、在故障诊断中的联合应用案例

案例：轴承故障诊断

1. 信号采集

   • 使用加速度传感器采集振动信号（采样率10kHz）。

2. 特征提取

   • 傅里叶变换：识别故障特征频率（如轴承外圈故障频率BPFO）。

   • 小波变换：定位故障发生的时刻（如冲击信号的时频分析）。

3. 诊断流程

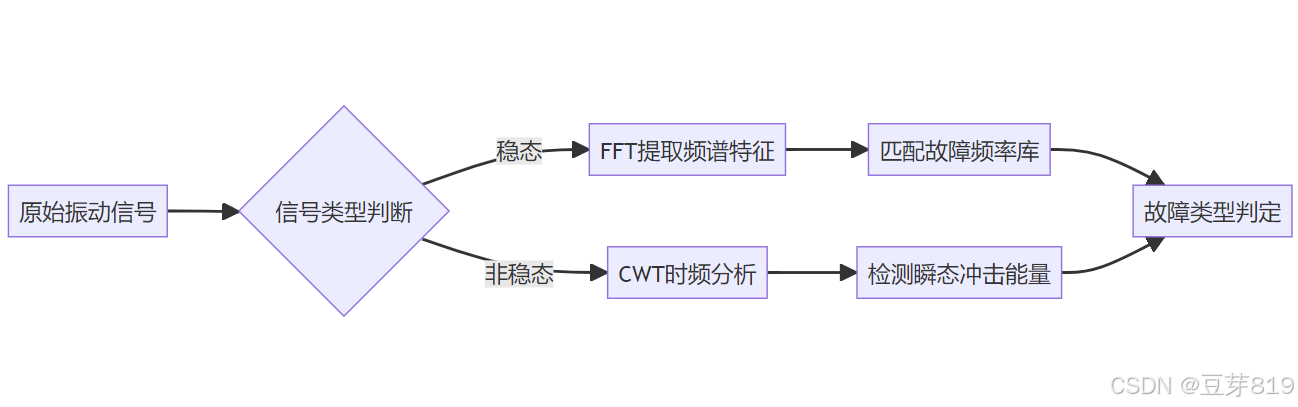
五、工程挑战与解决方案

1. 噪声干扰

• 对策：

  • 小波阈值去噪：软阈值处理高频细节系数。

  • 频带滤波：FFT后保留故障特征频段。

import pywt
import numpy as np
import matplotlib.pyplot as plt

def wavelet_denoise(noisy_signal, wavelet='db4', level=5):
    """
    使用离散小波变换（DWT）对信号进行去噪。

    参数:
    noisy_signal (array-like): 包含噪声的原始信号。
    wavelet (str): 选用的小波基，默认为 'db4'。
    level (int): 分解的层数，默认为 5。

    返回:
    array-like: 去噪后的信号。
    """
    # 小波分解
    wavelet_coeffs = pywt.wavedec(noisy_signal, wavelet, level=level)
    
    # 噪声估计
    sigma = np.median(np.abs(wavelet_coeffs[-1])) / 0.6745
    
    # 阈值计算
    threshold = sigma * np.sqrt(2*np.log(len(noisy_signal)))
    
    # 阈值处理
    thresholded_coeffs = [pywt.threshold(c, threshold, mode='soft') for c in wavelet_coeffs]
    
    # 小波重构
    denoised = pywt.waverec(thresholded_coeffs, wavelet)
    
    return denoised

# 示例信号
t = np.linspace(0, 1, 1000)
noisy_signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.random.randn(len(t))

# 去噪
denoised_signal = wavelet_denoise(noisy_signal)

# 可视化
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t, noisy_signal, label='Noisy Signal')
plt.title('Noisy Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()

plt.subplot(2, 1, 2)
plt.plot(t, denoised_signal, label='Denoised Signal', color='orange')
plt.title('Denoised Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.legend()

plt.tight_layout()
plt.show()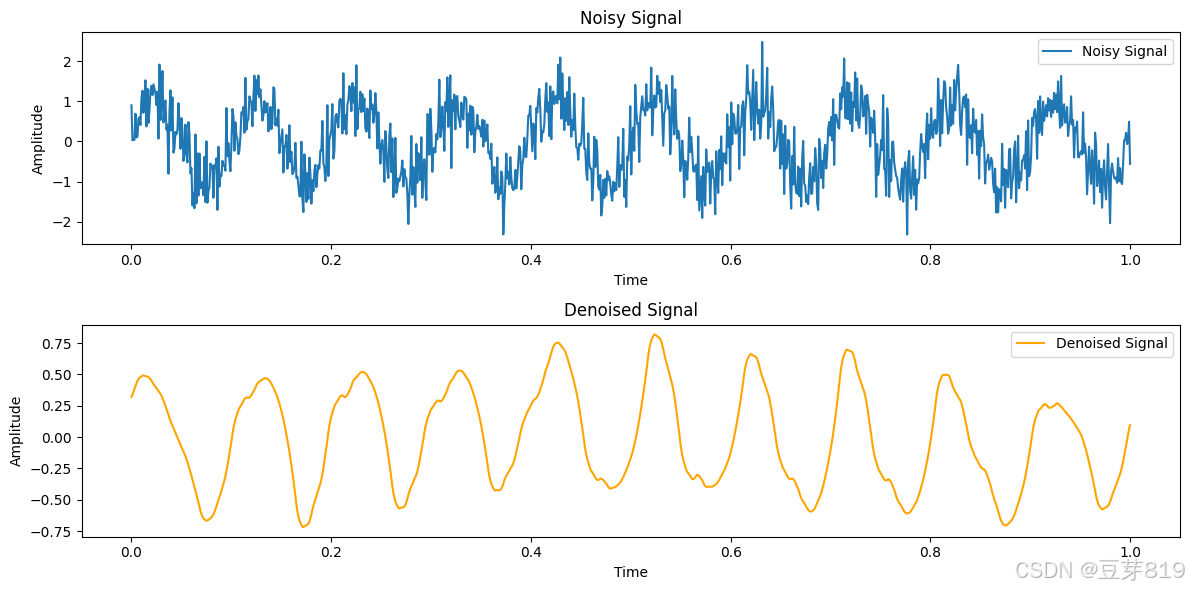

 

2. 计算效率优化

• 边缘计算：在设备端部署轻量化小波算法（TinyML）。

• GPU加速：使用CuPy库加速FFT（较NumPy快10倍+）。

import cupy as cp
x_gpu = cp.asarray(signal)
fft_gpu = cp.fft.fft(x_gpu)
fft_result = cp.asnumpy(fft_gpu)

3. 实际数据适配

• 非均匀采样：使用Lomb-Scargle周期算法（FFT变种）。

• 数据量不足：GAN生成合成故障数据扩充样本。

六、前沿技术融合

1. 深度学习与小波结合

• 小波卷积网络（Wavelet CNN）：

  • 用DWT替换CNN首层卷积，提取时频特征。

  • 代码框架：

class WaveletCNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.wavelet = DWTForward(J=3, wave='db4')  # 3层小波分解
        self.conv = nn.Conv2d(12, 64, kernel_size=3)  # 输入通道数=4子带×3层
    def forward(self, x):
        LL, coeffs = self.wavelet(x)  # 小波分解
        x = torch.cat([LL] + [c for c in coeffs], dim=1)
        return self.conv(x)

2. 数字孪生中的实时分析

• 架构设计：

  1. 传感器数据 → 边缘设备（FFT/小波预处理） → 云端数字孪生体。

  2. 孪生体实时映射故障位置，触发维护工单。

• 工具链：

  • 边缘端：TensorFlow Lite部署小波去噪模型。

  • 云端：Unity3D/Unreal Engine构建可视化孪生体。

总结

傅里叶分析是频域分析的基石，适合稳态信号；小波分析弥补其时间定位缺陷，专攻非平稳信号。在故障诊断中，二者常联合使用：

• FFT快速筛查频域异常，缩小故障范围。

• CWT/DWT精准定位故障时刻，区分瞬态与稳态特征。
  结合数字孪生技术，可构建从信号采集到虚拟映射的全链路智能诊断系统，推动预测性维护的落地。