【数学】三角函数及部分微积分函数图象整理
三角函数及部分微积分函数图象整理1. 三角函数1.1 cosx、secx1.2 sinx、cscx1.3 tanx、cotx1.4 sec^2^x、tanx2.反三角函数2.1 arcsinx、arctanx2.2 arccosx使用Desmos绘图: https://www.desmos.com/calculator1. 三角函数1.1 cosx、secx1.2 sinx、cscx...
使用Desmos绘图: https://www.desmos.com/calculator
1. 三角函数
1.1 cosx、secx
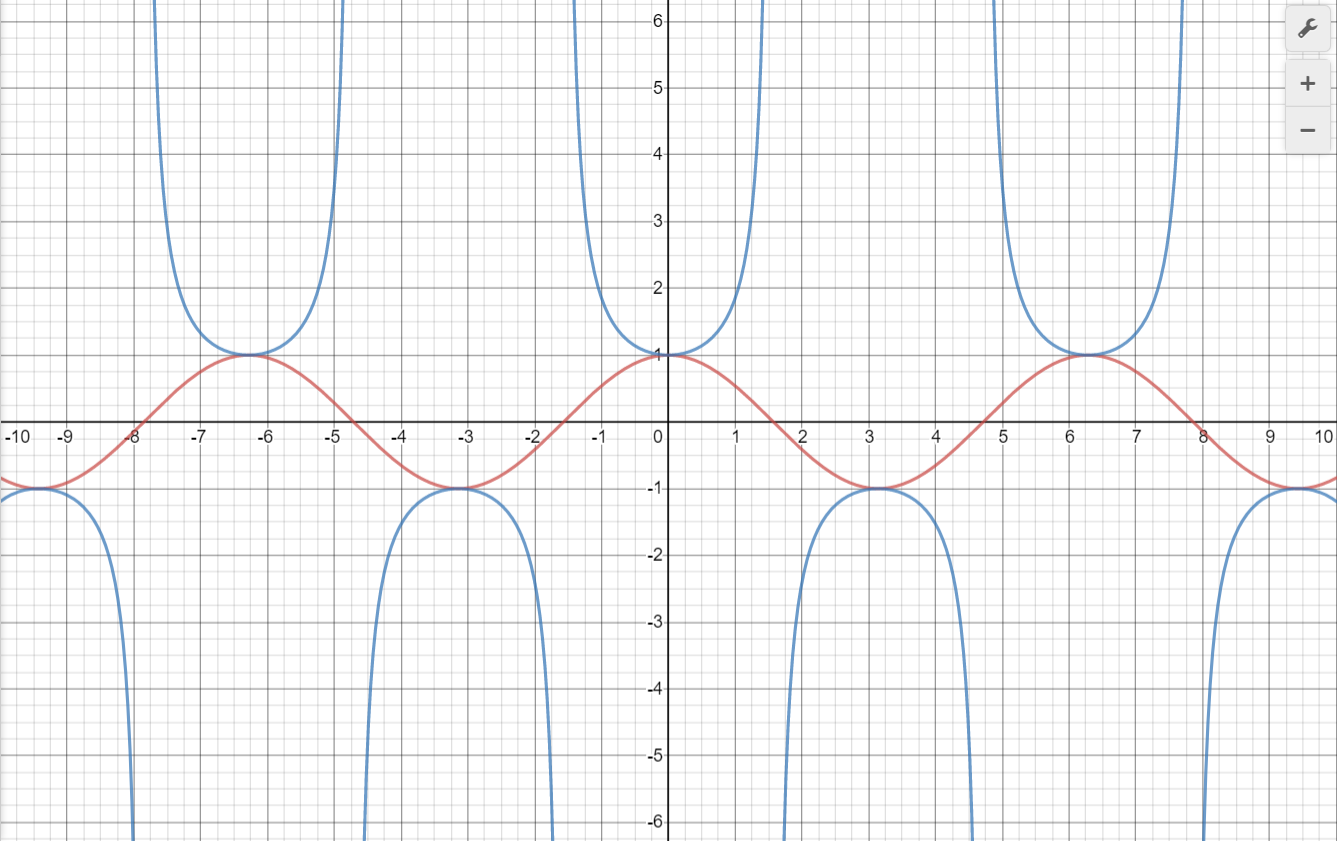
1.2 sinx、cscx
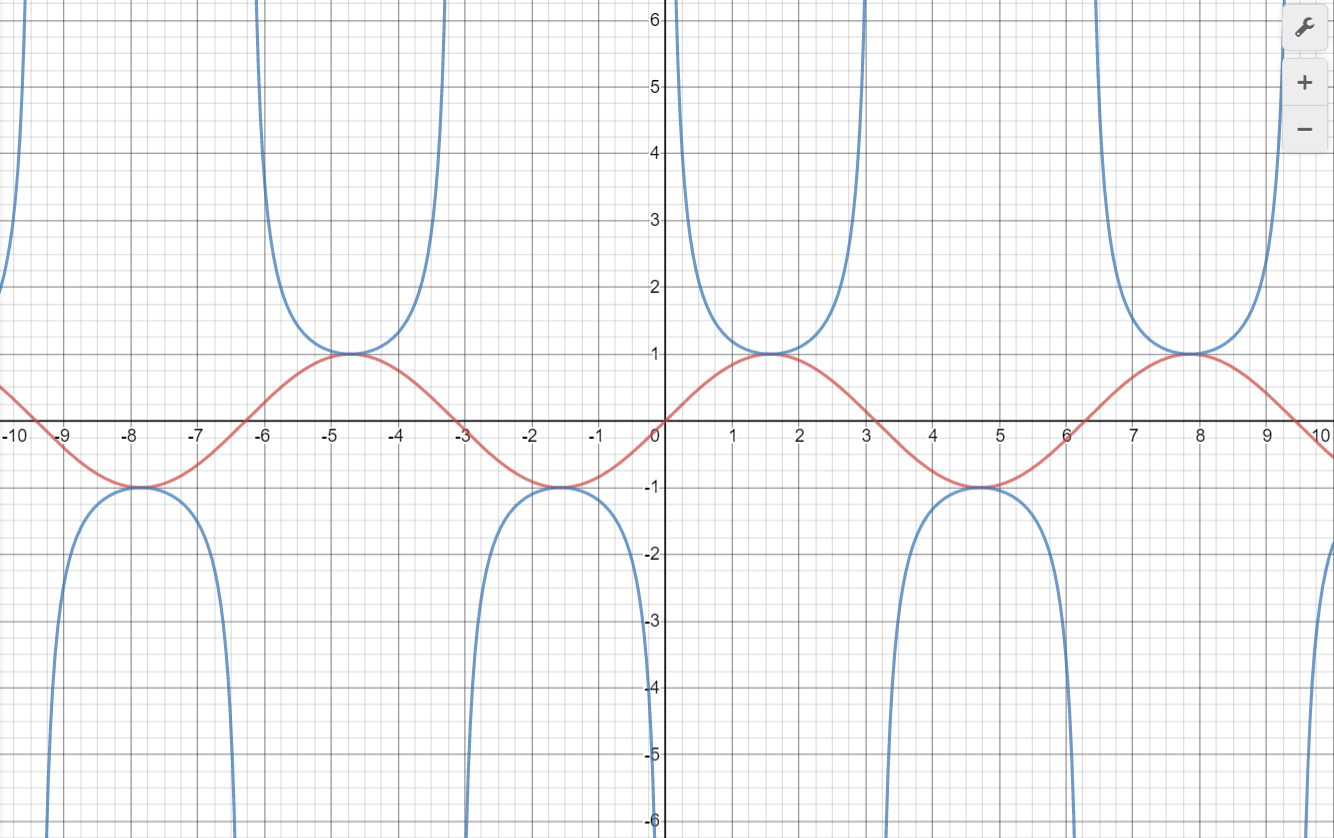
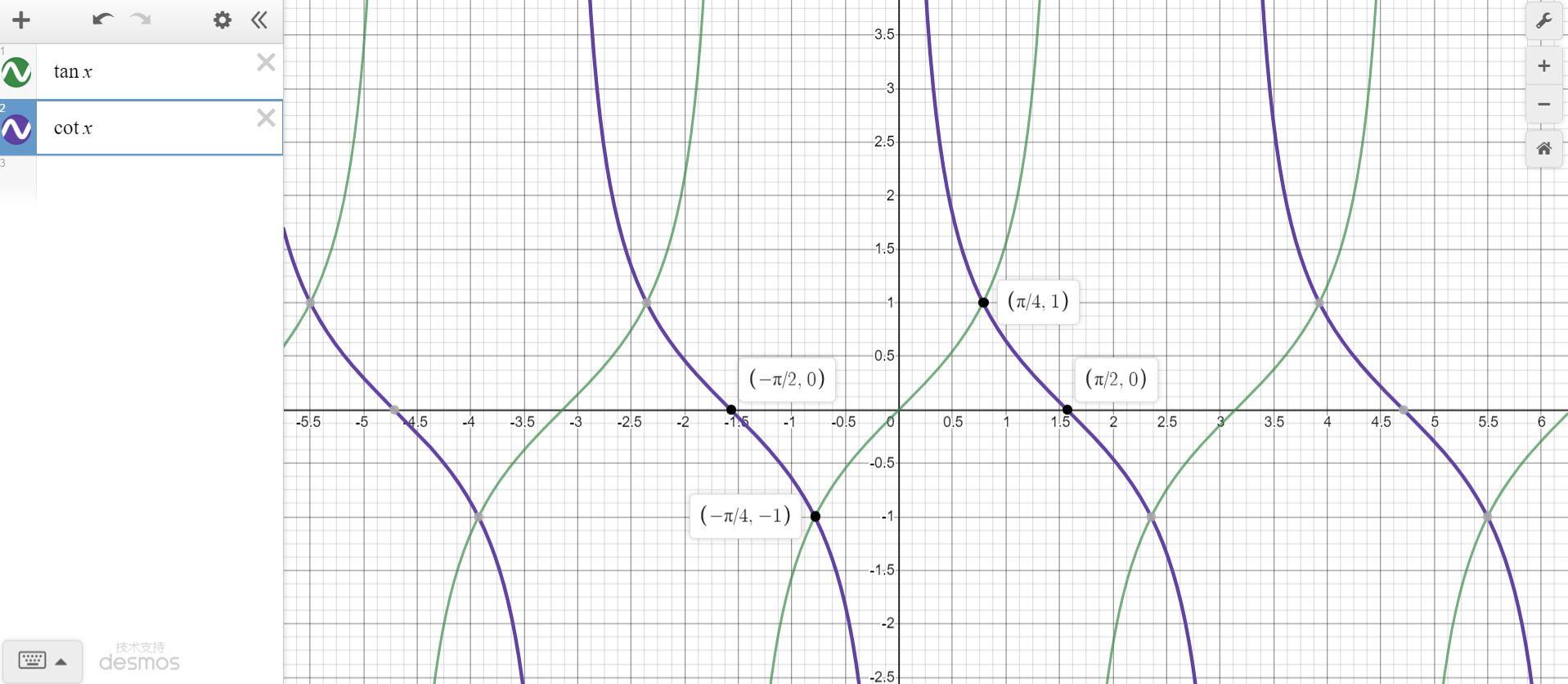
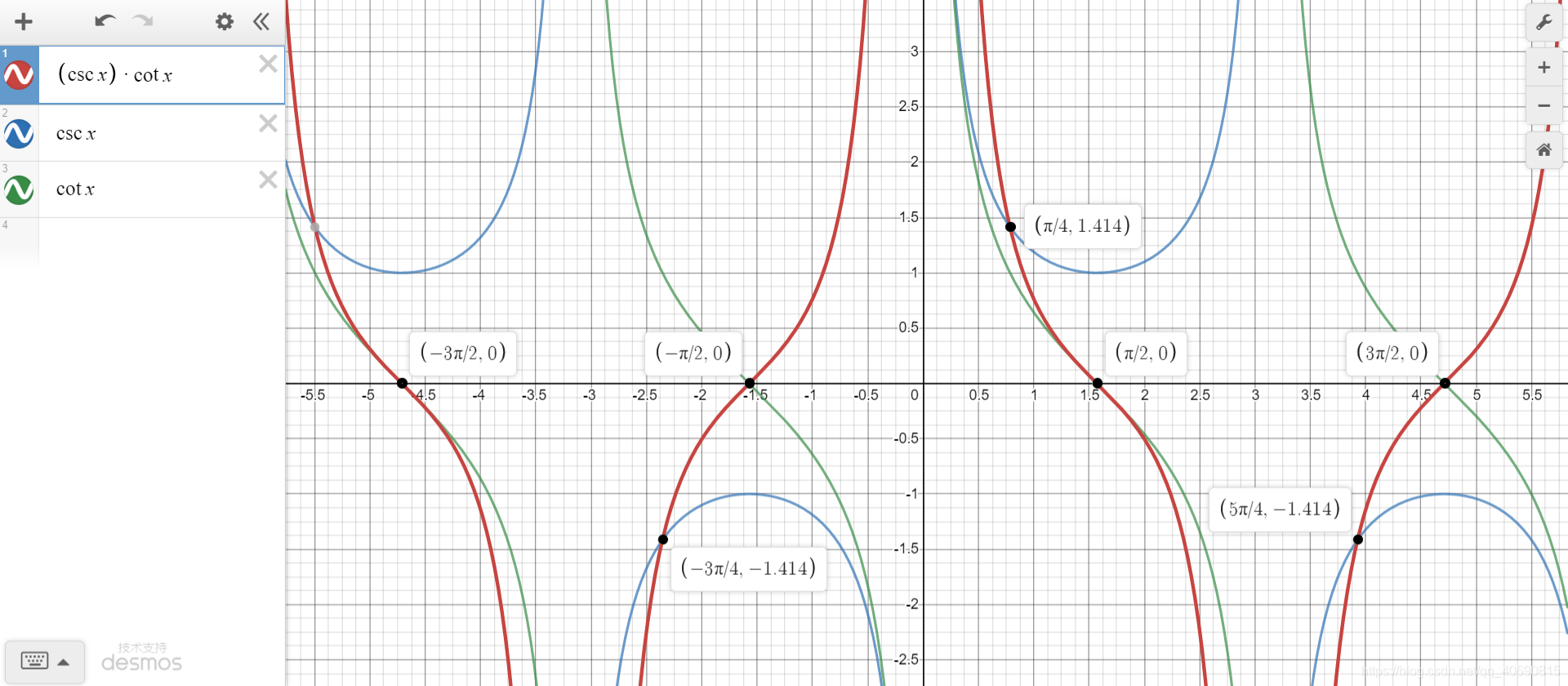
1.3 tanx、cotx
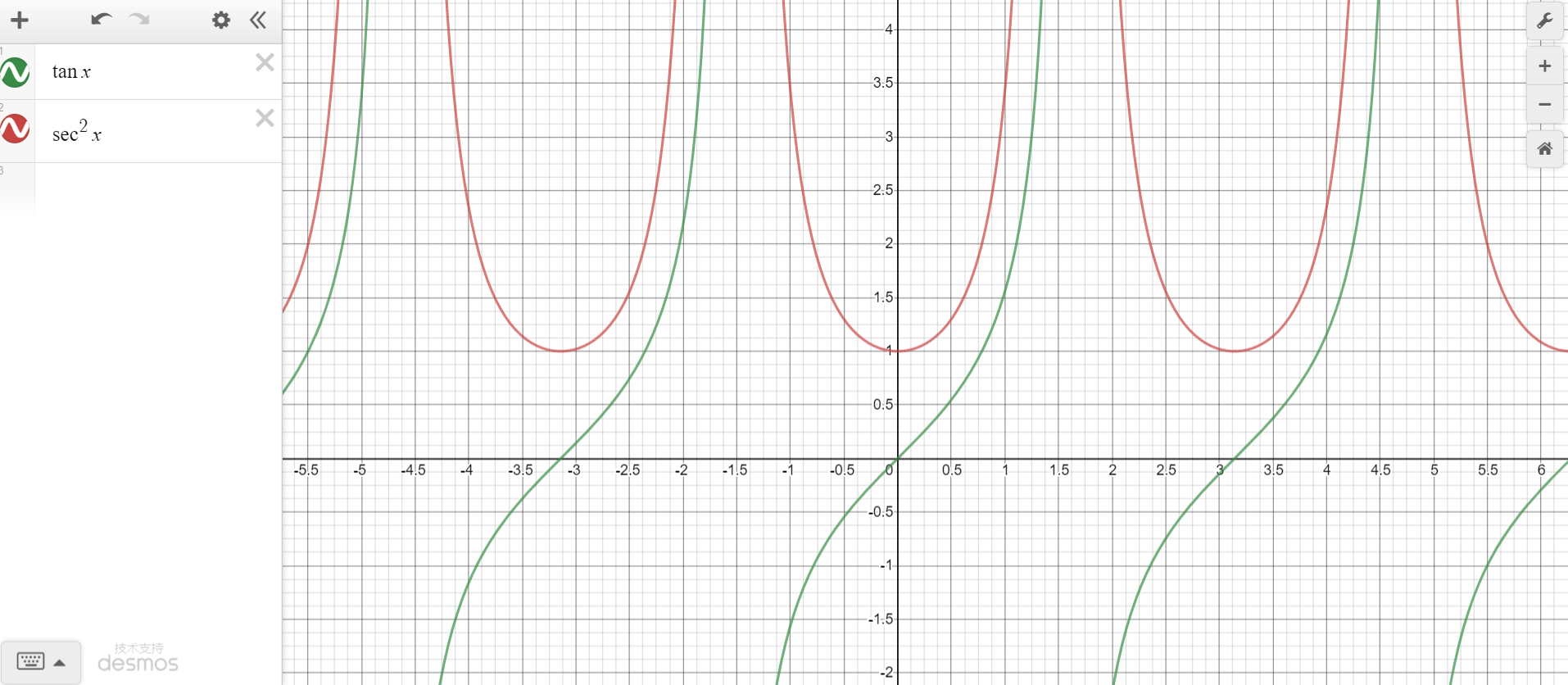
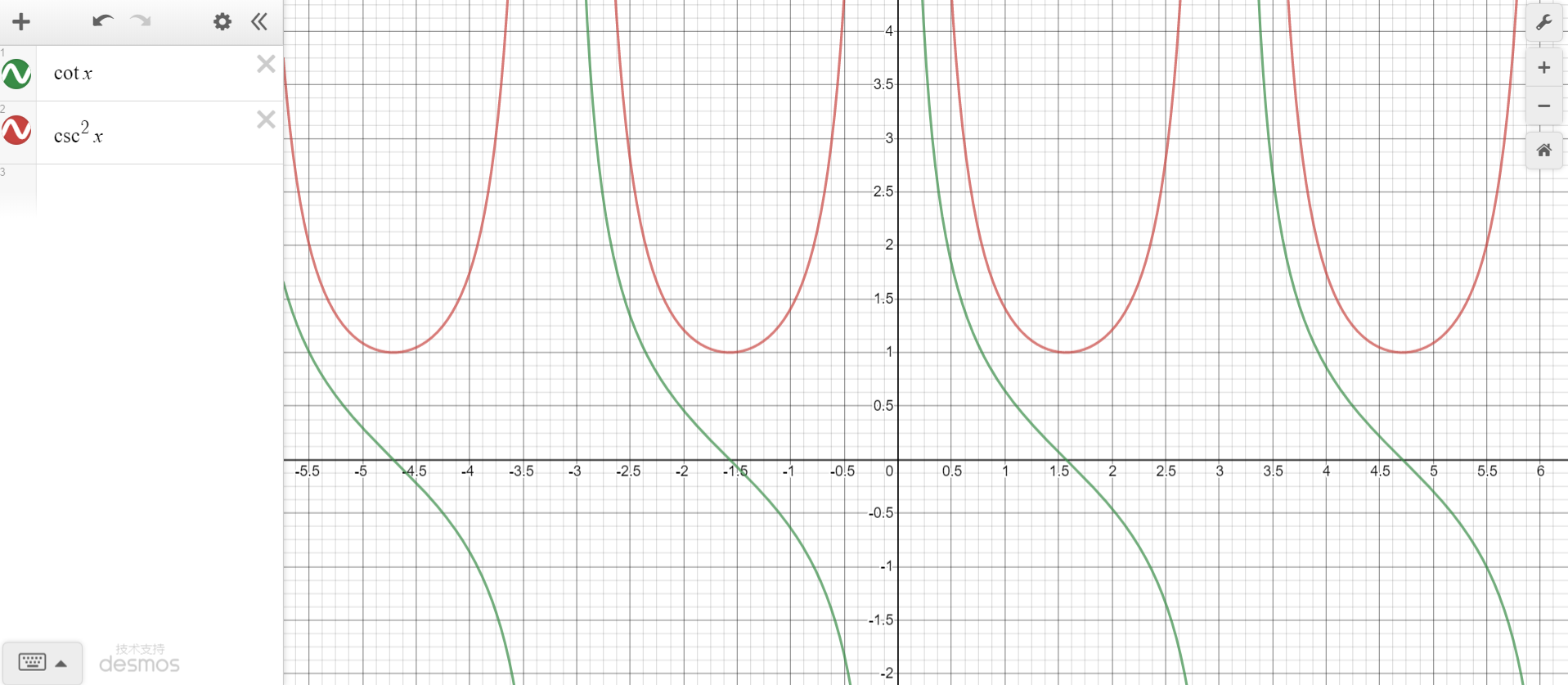
1.4 ∫ s e c 2 x d x 、 ∫ c s c 2 x d x \int sec^2xdx、\int csc^2xdx ∫sec2xdx、∫csc2xdx
∫ s e c 2 x d x = t a n x + C \int sec^2x dx =tanx + C ∫sec2xdx=tanx+C
∫ c s c 2 x d x = c o t x + C \int csc^2x dx =cotx + C ∫csc2xdx=cotx+C
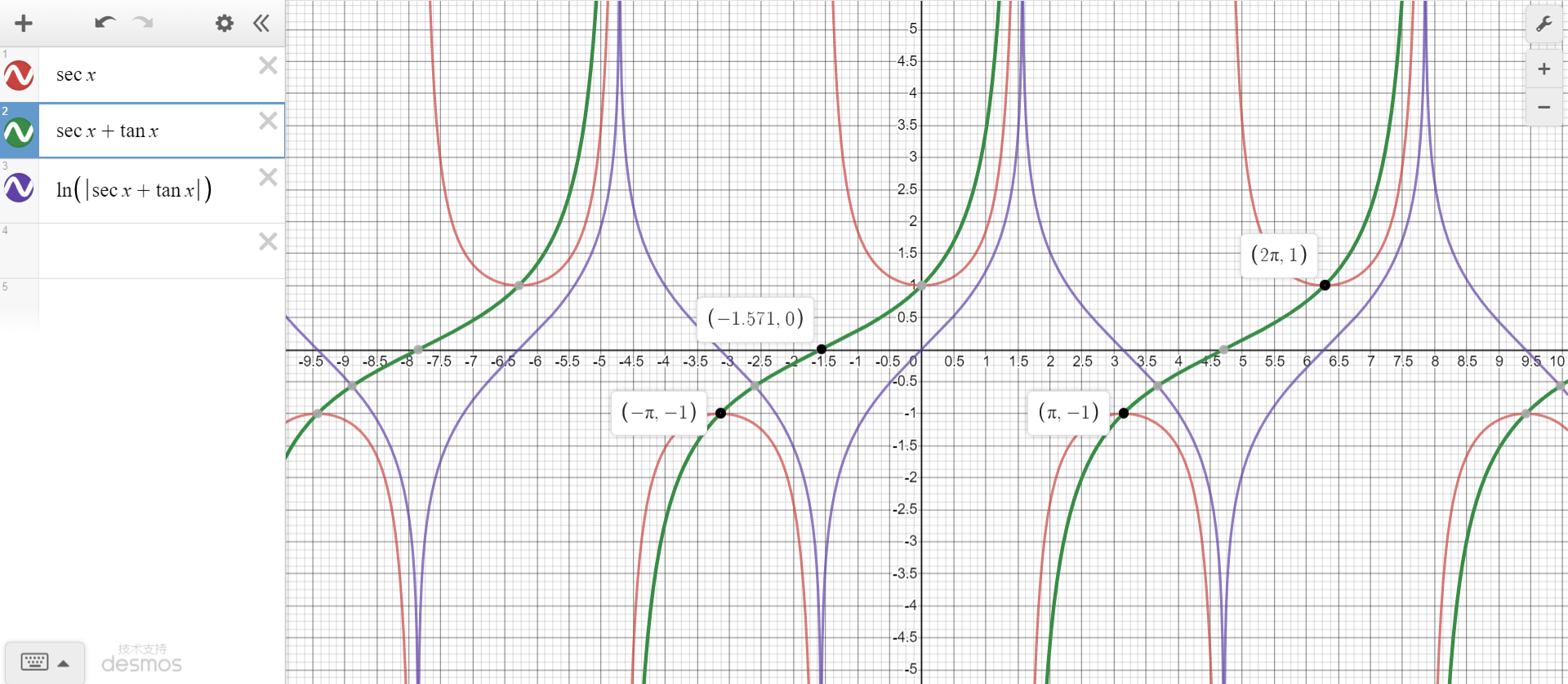
1.5 ∫ s e c d x 、 ∫ c s c d x \int secdx、\int cscdx ∫secdx、∫cscdx
∫ s e c x d x = l n ∣ s e c x + t a n x ∣ + C \int secxdx = ln|secx+tanx|+C ∫secxdx=ln∣secx+tanx∣+C
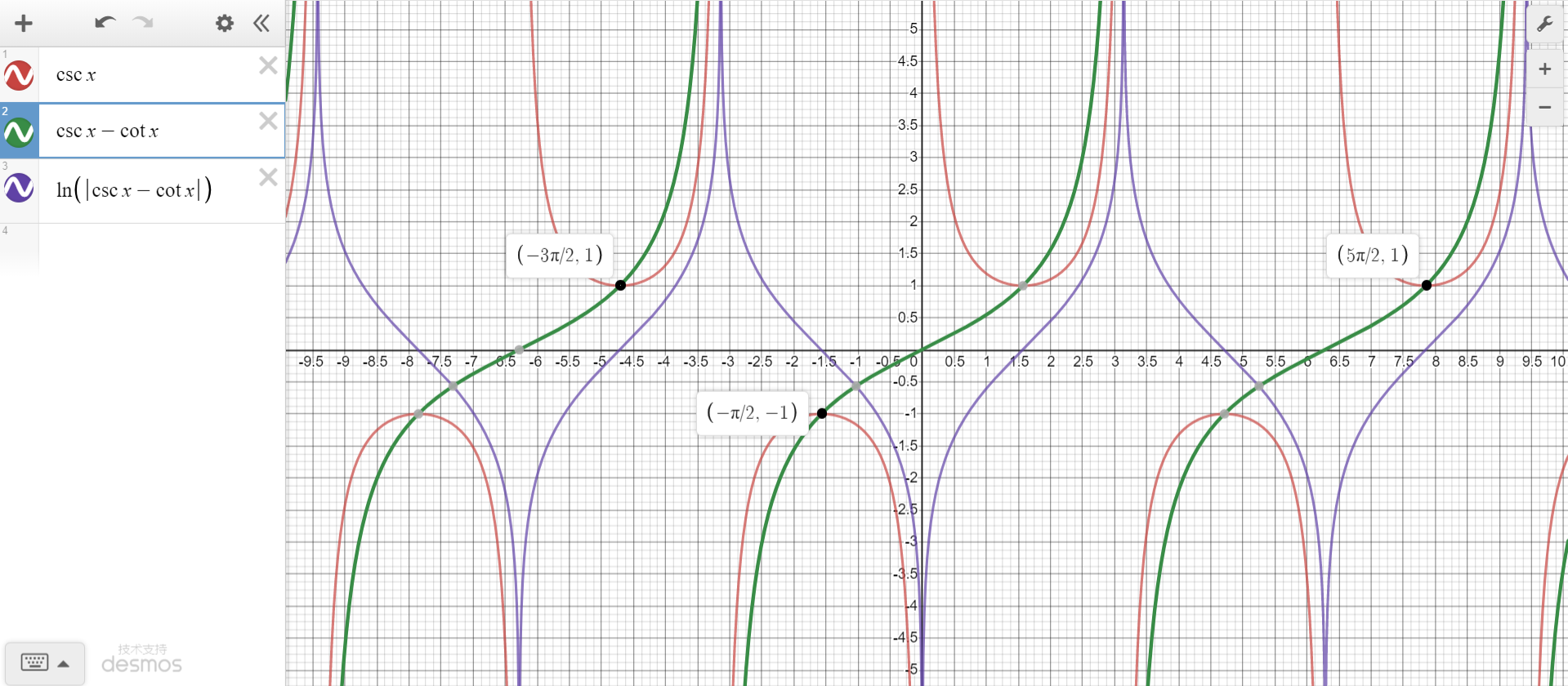
∫ c s c x d x = l n ∣ c s c x − c o t x ∣ + C \int cscxdx = ln|cscx-cotx|+C ∫cscxdx=ln∣cscx−cotx∣+C
1.6 ∫ s e c x t a n x d x 、 ∫ c s c x c o t x d x \int secxtanxdx、\int cscxcotxdx ∫secxtanxdx、∫cscxcotxdx
∫ s e c x t a n x d x = ∫ s i n x c o s 2 x d x = s e c x + C \int secxtanxdx=\int \frac{sinx}{cos^2x}dx=secx+C ∫secxtanxdx=∫cos2xsinxdx=secx+C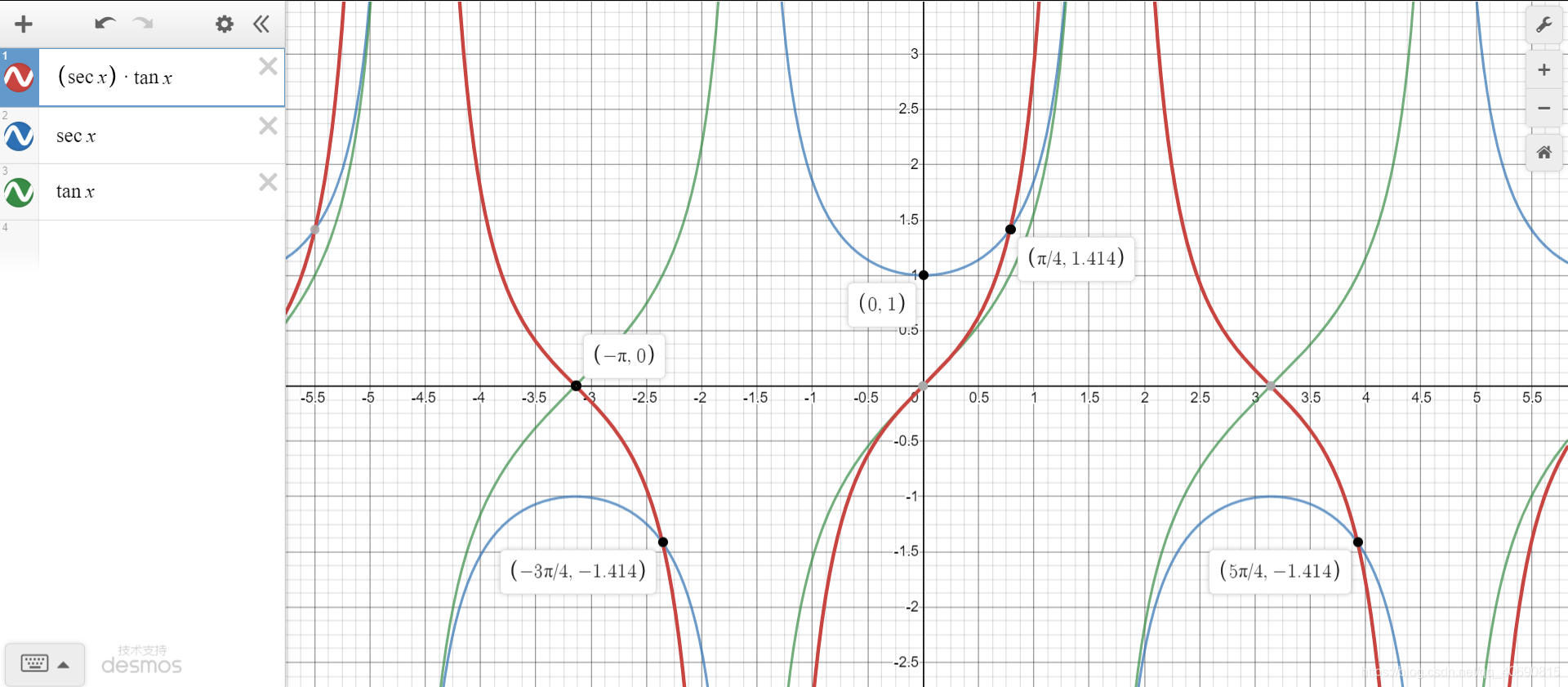
∫ c s c x c o t x d x = ∫ c o s x s i n 2 x d x = c s c x + C \int cscxcotxdx=\int \frac{cosx}{sin^2x}dx=cscx+C ∫cscxcotxdx=∫sin2xcosxdx=cscx+C
2. 反三角函数
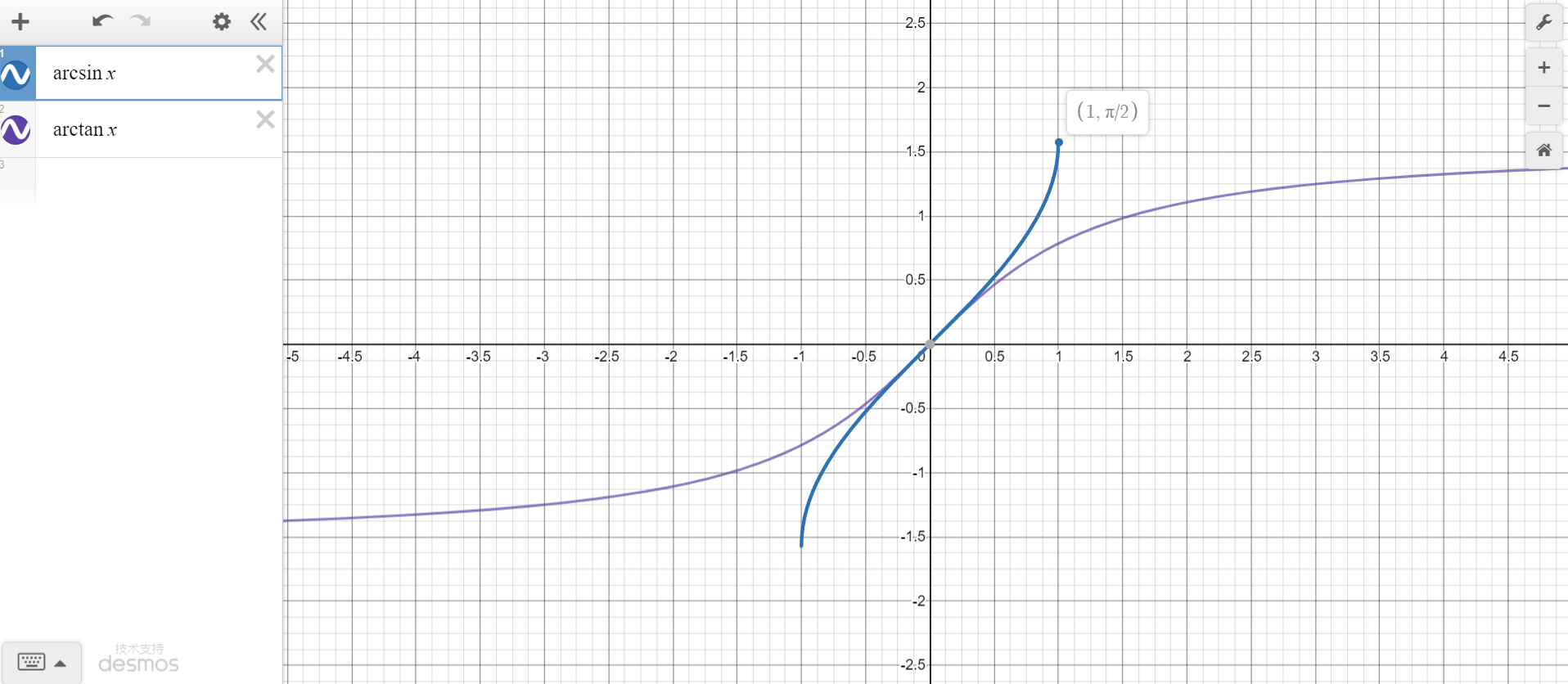
2.1 arcsinx、arctanx
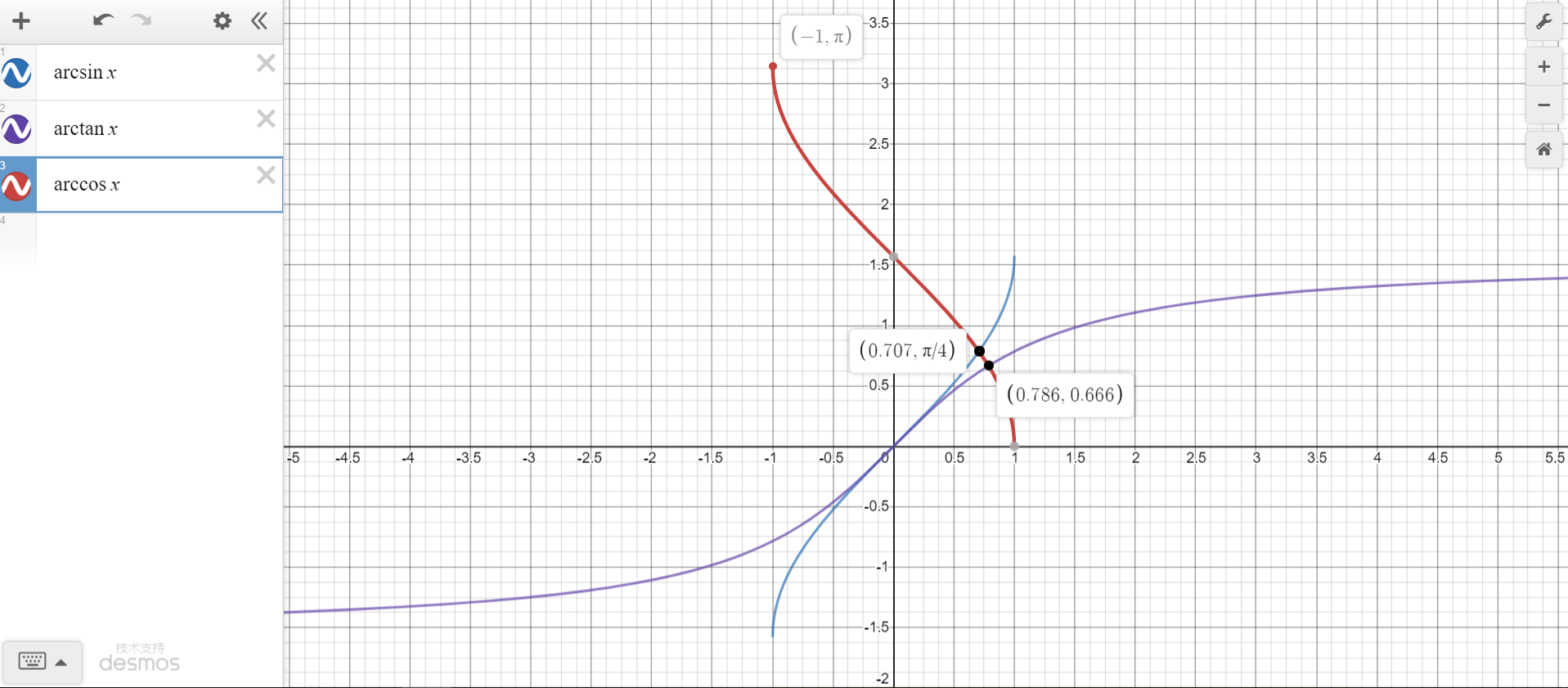
2.2 arccosx
3. 代数
3.1 ∫ 1 1 − x 2 d x \int \frac{1}{\sqrt{1-x^2}}dx ∫1−x21dx
∫ 1 a 2 − x 2 d x = a r c s i n x a + C \int \frac{1}{\sqrt{a^2-x^2}}dx=arcsin\frac{x}{a}+C ∫a2−x21dx=arcsinax+C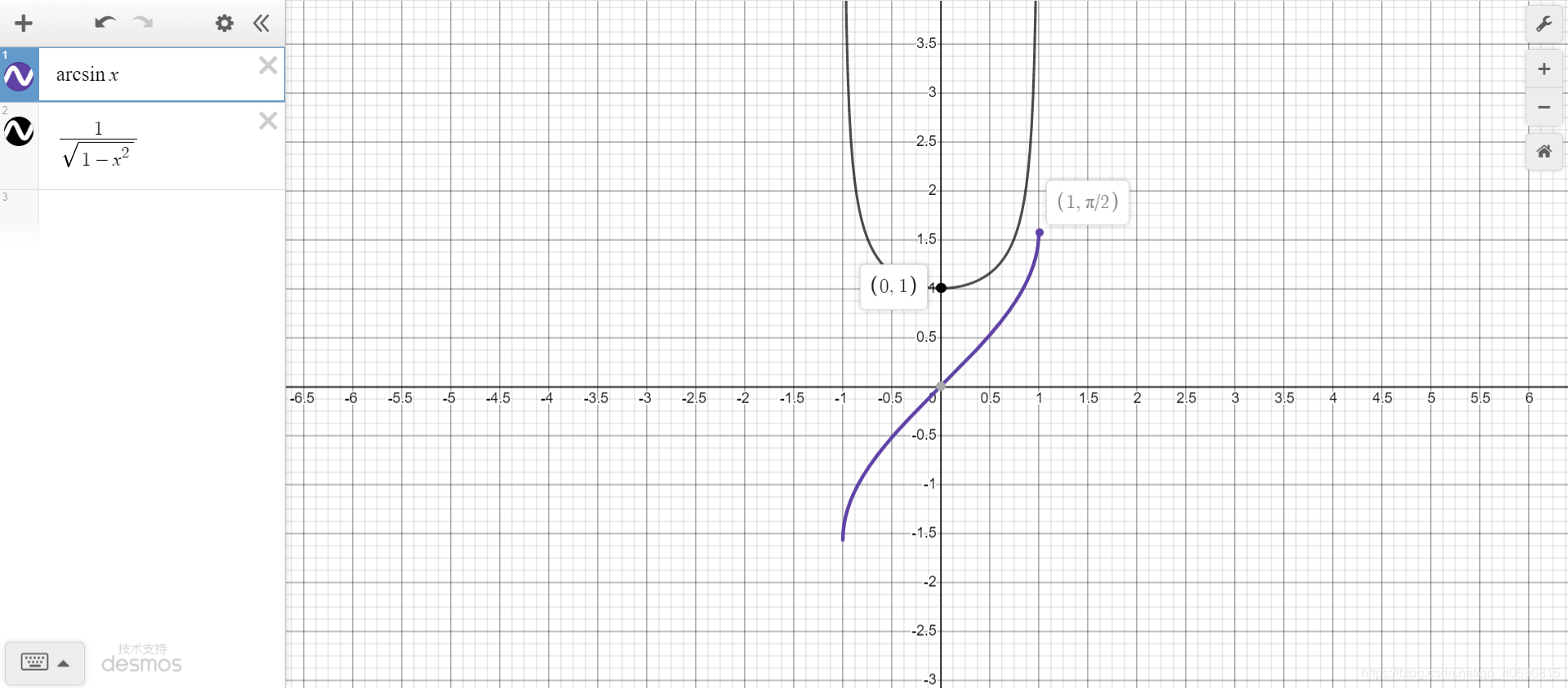
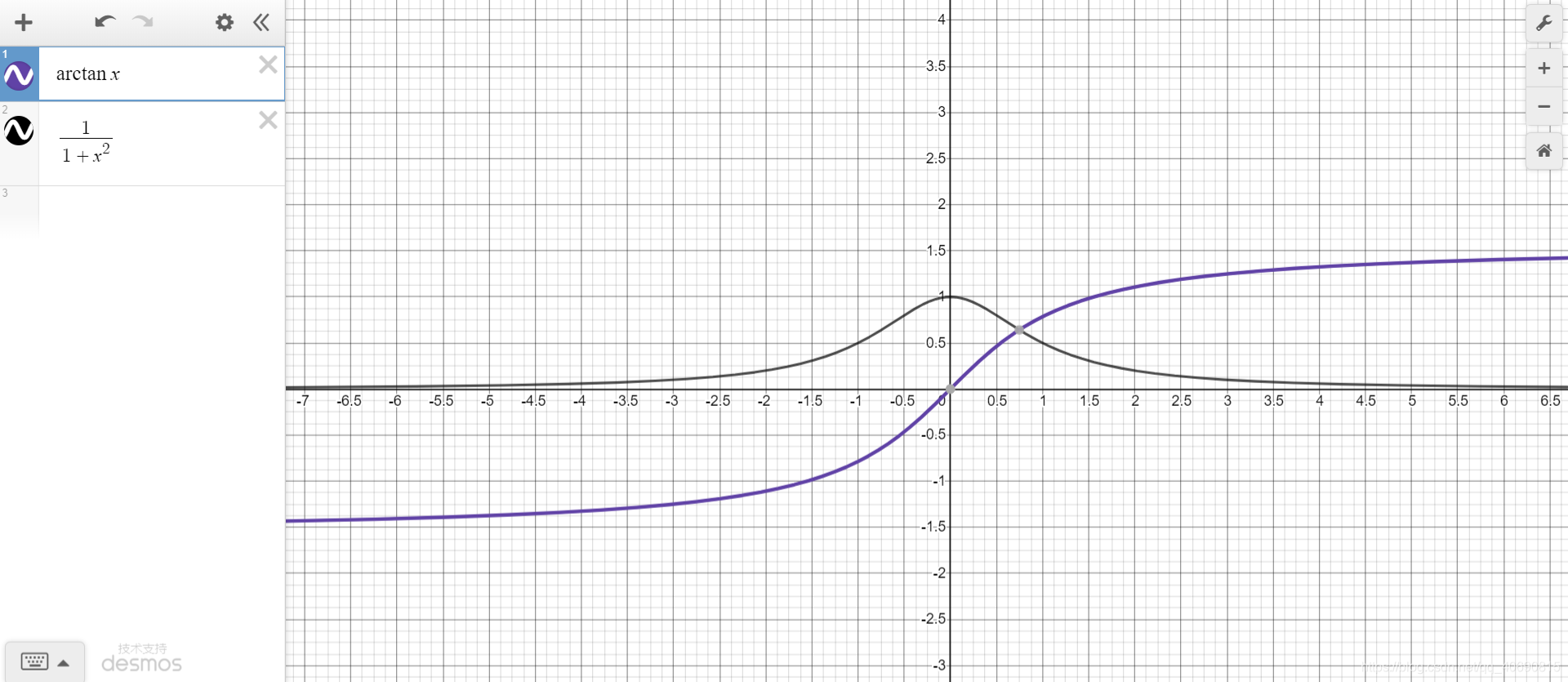
3.2 ∫ 1 1 + x 2 d x \int \frac{1}{1+x^2}dx ∫1+x21dx
∫ 1 a 2 + x 2 d x = 1 a a r c t a n x a + C \int \frac{1}{a^2+x^2}dx=\frac{1}{a}arctan\frac{x}{a}+C ∫a2+x21dx=a1arctanax+C
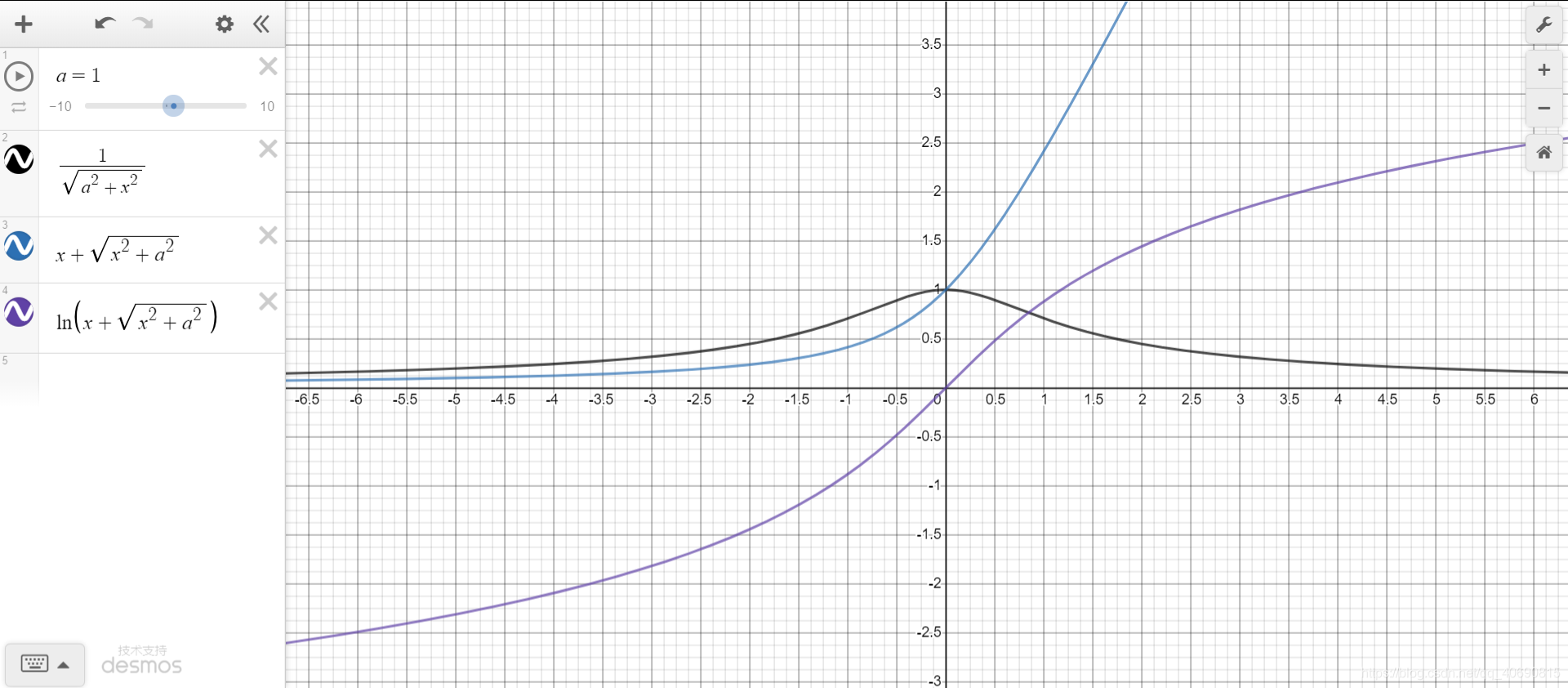
3.3 ∫ 1 x 2 ± a 2 d x \int \frac{1}{\sqrt{x^2\pm a^2}}dx ∫x2±a21dx
∫ 1 x 2 + a 2 d x = l n ( x + x 2 + a 2 ) + C \int \frac{1}{\sqrt{x^2+a^2}}dx=ln(x+\sqrt{x^2+a^2})+C ∫x2+a21dx=ln(x+x2+a2)+C
∫ 1 x 2 − a 2 d x = l n ∣ x + x 2 − a 2 ∣ + C \int \frac{1}{\sqrt{x^2-a^2}}dx=ln|x+\sqrt{x^2-a^2}|+C ∫x2−a21dx=ln∣x+x2−a2∣+C
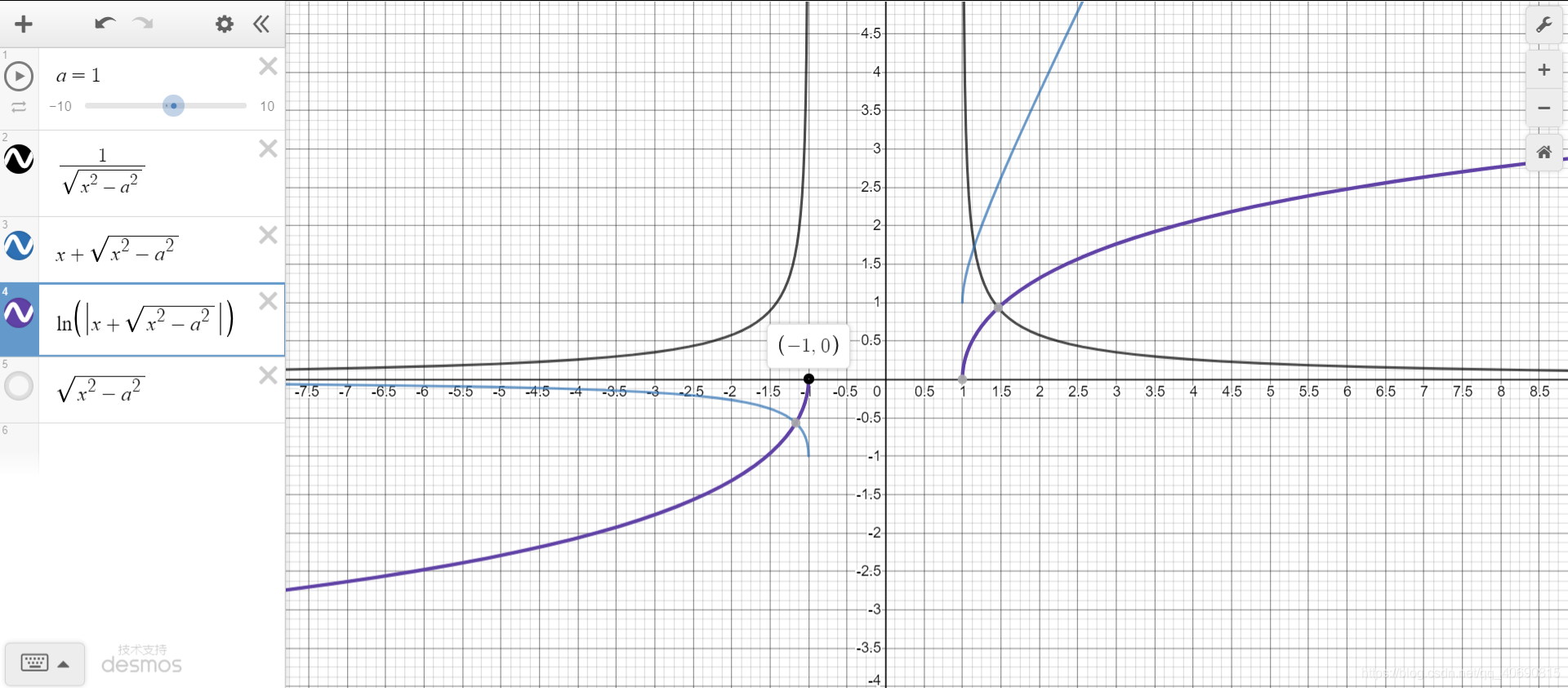
3.4 ∫ 1 x 2 − a 2 d x \int \frac{1}{x^2- a^2}dx ∫x2−a21dx
∫ 1 x 2 − a 2 d x = 1 2 a l n ∣ x − a x + a ∣ + C \int \frac{1}{x^2- a^2}dx=\frac{1}{2a}ln|\frac{x-a}{x+a}|+C ∫x2−a21dx=2a1ln∣x+ax−a∣+C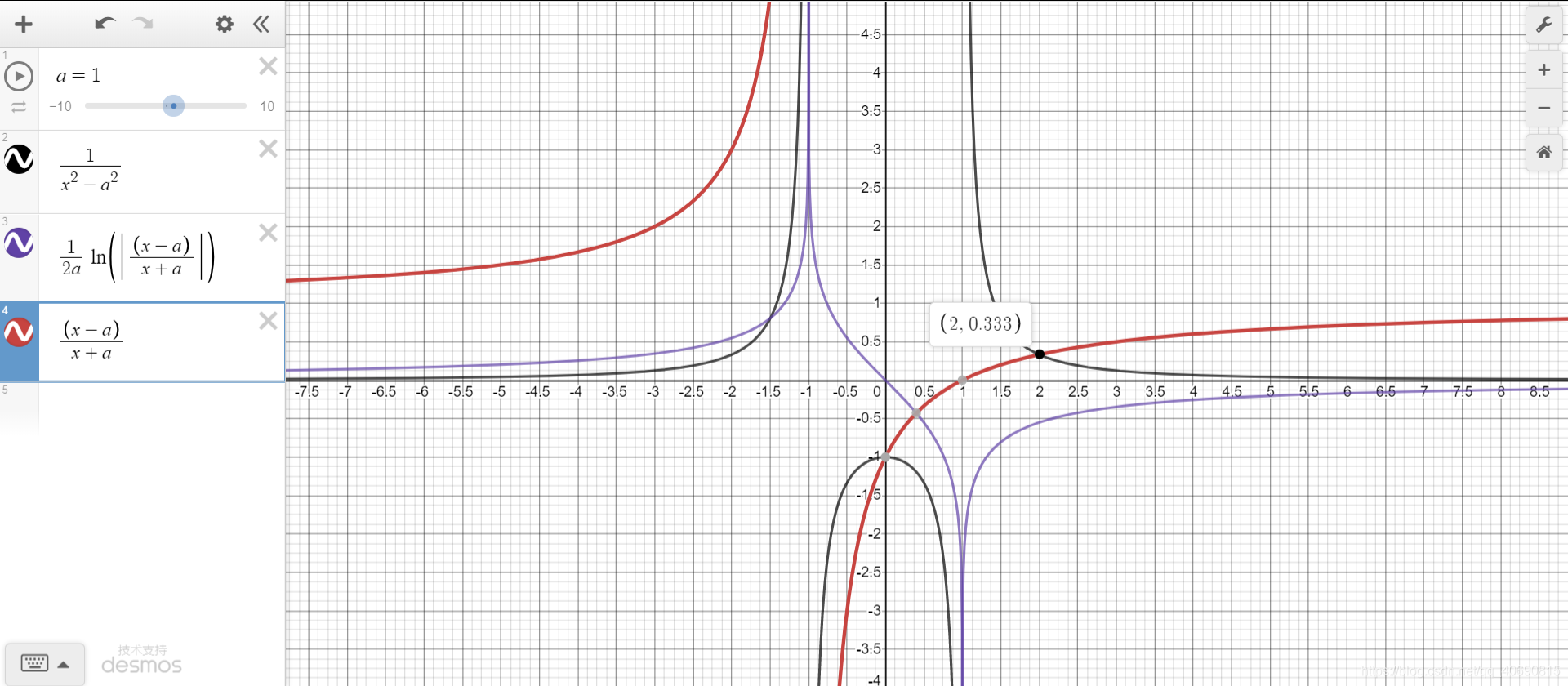
3.5 ∫ a 2 − x 2 d x \int \sqrt{a^2-x^2}dx ∫a2−x2dx
∫ a 2 − x 2 d x = a 2 2 a r c s i n x a + 1 2 x a 2 − x 2 + C \int \sqrt{a^2-x^2}dx=\frac{a^2}{2}arcsin\frac{x}{a}+\frac{1}{2}x\sqrt{a^2-x^2}+C ∫a2−x2dx=2a2arcsinax+21xa2−x2+C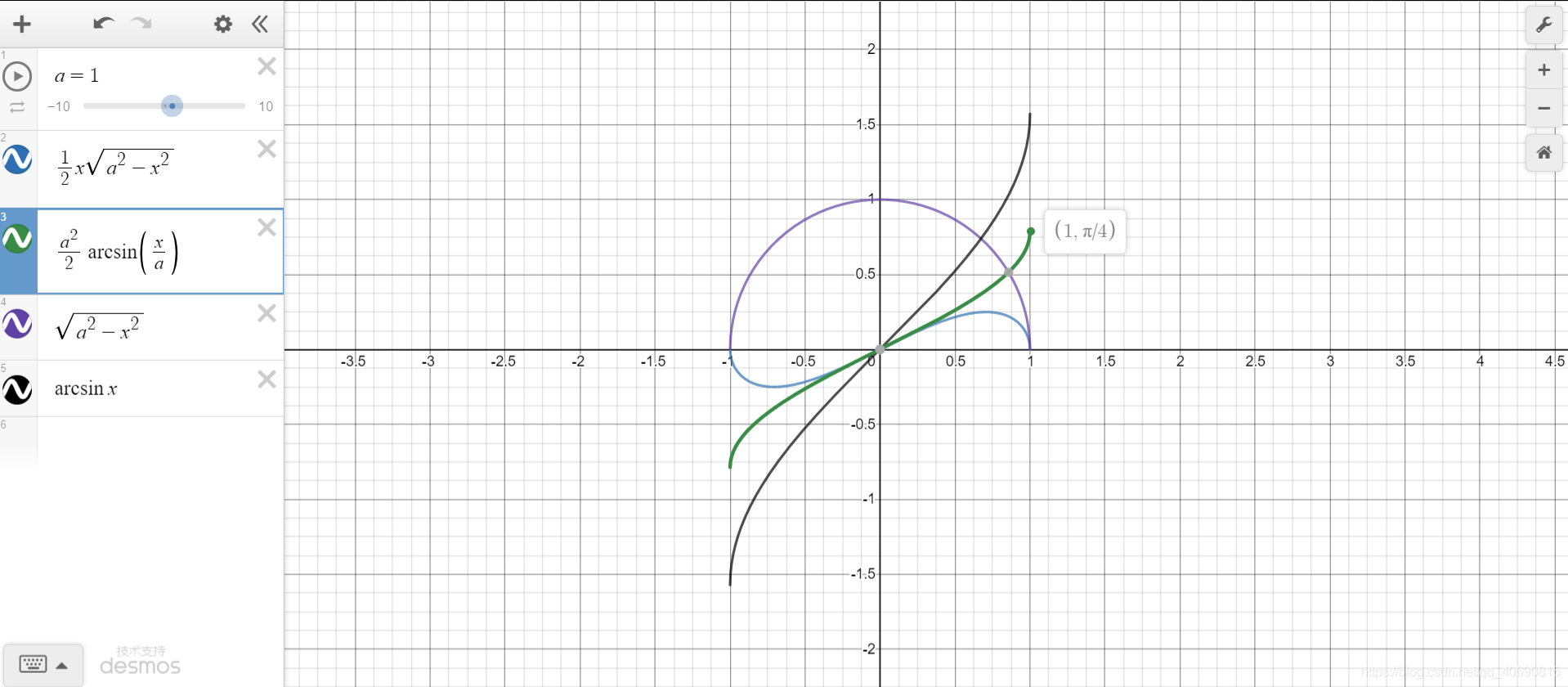
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容








所有评论(0)