数学分析讲义习题解答:(二)
可数与不可数,Schroeder−BernsteinSchroeder-BernsteinSchroeder−Bernstein定理AAA.实数的性质A1)A1)A1) 假设非空集合X⊂RX ⊂ RX⊂R有上界并且实数MMM是XXX的上界。证明,如下两个命题等价:– M=supXM=\sup XM=supX– 对任意的ε>0ε>0ε>0,都存在x∈Xx∈Xx∈X,使得x>
可数与不可数,Schroeder−BernsteinSchroeder-BernsteinSchroeder−Bernstein定理
A:A:A:实数的性质
A1)A1)A1) 假设非空集合X⊂RX ⊂ RX⊂R有上界并且实数MMM是XXX的上界。证明,如下两个命题等价:
– M=supXM=\sup XM=supX
– 对任意的ε>0ε>0ε>0,都存在x∈Xx∈Xx∈X,使得x>M−εx>M-εx>M−ε
证明:M=supXM=\sup XM=supX,等价于MMM是上界集的最小元,设ε>0ε>0ε>0,则有M−ε<MM-ε<MM−ε<M,而第二个条件等价于M−εM-εM−ε不是XXX的上界,根据定义两者等价是显然的。
A2)A2)A2) 证明,每个⾮空开区间都包含⽆限多个有理数。
证明:设I=(a,b)I=(a,b)I=(a,b)是一个非空开区间即a<ba<ba<b,那么根据有理数在实数中的稠密性一定存在l,r∈Q,a<l<a+b2<r<bl,r\in\mathbb{Q},a<l<\frac{a+b}{2}<r<bl,r∈Q,a<l<2a+b<r<b,定义序列xn=l+r−l2nx_n=l+\frac{r-l}{2^n}xn=l+2nr−l,这是一个严格递减的序列从而没有相同的两项,并且根据有理数对四则运算的封闭性{xn}⊂Q\{x_n\}\sub\mathbb{Q}{xn}⊂Q,并且a<l<xn<r<ba<l<x_n<r<ba<l<xn<r<b即{xn}⊂(a,b)\{x_n\}\sub(a,b){xn}⊂(a,b),从而III中包含了无穷多个有理数,得证。
A3)A3)A3) (X,d)(X,d)(X,d)是距离空间,Y⊂XY⊂XY⊂X。我们定义YYY上的距离函数:
dY:Y×Y→R,(y1,y2)↦dY(y1,y2)=d(y1,y2)d_Y:Y×Y→R,(y_1, y_2)\mapsto d_Y (y_1, y_2) = d(y_1, y_2)dY:Y×Y→R,(y1,y2)↦dY(y1,y2)=d(y1,y2)
证明,dYd_YdY是YYY上的距离函数,从而(Y,dY)(Y,d_Y)(Y,dY)是度量空间。我们称dYd_YdY是ddd在YYY上的诱导度量,(Y,dY)(Y,d_Y)(Y,dY)称作是(X,d)(X,d)(X,d)的子(度量)空间。
证明:验证定义即可。设x,y,z∈Yx,y,z\in Yx,y,z∈Y:
1)1)1) 正定性:dY(x,y)=d(x,y)≥0d_Y(x,y)=d(x,y)\ge0dY(x,y)=d(x,y)≥0,dY(x,y)=0d_Y(x,y)=0dY(x,y)=0当且仅当d(x,y)=0d(x,y)=0d(x,y)=0当且仅当x=yx=yx=y。
2)2)2) 对称性:dY(x,y)=d(x,y)=d(y,x)=dY(y,x)d_Y(x,y)=d(x,y)=d(y,x)=d_Y(y,x)dY(x,y)=d(x,y)=d(y,x)=dY(y,x)。
3)3)3) 三角不等式:dY(x,y)+dY(y,z)=d(x,y)+d(y,z)≥d(x,z)=dY(x,z)d_Y(x,y)+d_Y(y,z)=d(x,y)+d(y,z)\ge d(x,z)=d_Y(x,z)dY(x,y)+dY(y,z)=d(x,y)+d(y,z)≥d(x,z)=dY(x,z)。
A4)A4)A4) Rn=R×⋅⋅⋅×R(n个)={(x1,⋅⋅⋅,xn)∣x1,⋅⋅⋅,xn∈R}\R^n=\R\times\cdot\cdot\cdot\times\R(n个)=\{(x_1,\cdot\cdot\cdot,x_n)|x_1,\cdot\cdot\cdot,x_n\in\R\}Rn=R×⋅⋅⋅×R(n个)={(x1,⋅⋅⋅,xn)∣x1,⋅⋅⋅,xn∈R}。对于x,y∈Rnx,y\in\R^nx,y∈Rn,我们定义:
d(x,y)=(x1−y1)2+⋅⋅⋅+(xn−yn)2,x=(x1,⋅⋅⋅,xn),y=(y1,⋅⋅⋅,yn) d(x,y)=\sqrt{(x_1-y_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2},x=(x_1,\cdot\cdot\cdot,x_n),y=(y_1,\cdot\cdot\cdot,y_n) d(x,y)=(x1−y1)2+⋅⋅⋅+(xn−yn)2,x=(x1,⋅⋅⋅,xn),y=(y1,⋅⋅⋅,yn)
证明,(Rn,d)(\R^n,d)(Rn,d)是度量空间。
证明:逐一验证定义。设x,y,z∈Rnx,y,z\in\R^nx,y,z∈Rn,其中x=(x1,⋅⋅⋅,xn),y=(y1,⋅⋅⋅,yn),z=(z1,⋅⋅⋅,zn)x=(x_1,\cdot\cdot\cdot,x_n),y=(y_1,\cdot\cdot\cdot,y_n),z=(z_1,\cdot\cdot\cdot,z_n)x=(x1,⋅⋅⋅,xn),y=(y1,⋅⋅⋅,yn),z=(z1,⋅⋅⋅,zn):
1)1)1) 正定性:d(x,y)=(x1−y1)2+⋅⋅⋅+(xn−yn)2≥0d(x,y)=\sqrt{(x_1-y_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2}\ge0d(x,y)=(x1−y1)2+⋅⋅⋅+(xn−yn)2≥0,且d(x,y)=(x1−y1)2+⋅⋅⋅+(xn−yn)2=0d(x,y)=\sqrt{(x_1-y_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2}=0d(x,y)=(x1−y1)2+⋅⋅⋅+(xn−yn)2=0当且仅当(x1−y1)2+⋅⋅⋅+(xn−yn)2=0(x_1-y_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2=0(x1−y1)2+⋅⋅⋅+(xn−yn)2=0,由于(xi−yi)2≥0(x_i-y_i)^2\ge0(xi−yi)2≥0取等当且仅当xi=yix_i=y_ixi=yi,从而d(x,y)=0d(x,y)=0d(x,y)=0当且仅当x1=y1,⋅⋅⋅,xn=ynx_1=y_1,\cdot\cdot\cdot,x_n=y_nx1=y1,⋅⋅⋅,xn=yn,即x=yx=yx=y。
2)2)2) 对称性:d(x,y)=(x1−y1)2+⋅⋅⋅+(xn−yn)2=(y1−x1)2+⋅⋅⋅+(yn−xn)2=d(y,x)d(x,y)=\sqrt{(x_1-y_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2}=\sqrt{(y_1-x_1)^2+\cdot\cdot\cdot+(y_n-x_n)^2}=d(y,x)d(x,y)=(x1−y1)2+⋅⋅⋅+(xn−yn)2=(y1−x1)2+⋅⋅⋅+(yn−xn)2=d(y,x)。
3)3)3) 三角不等式:(d(x,y)+d(y,z))2=((x1−y1)2+⋅⋅⋅+(xn−yn)2+(y1−z1)2+⋅⋅⋅+(yn−zn)2)2=(x1−y1)2+⋅⋅⋅+(xn−yn)2+(y1−z1)2+⋅⋅⋅+(yn−zn)2+2((x1−y1)2+⋅⋅⋅+(xn−yn)2)((y1−z1)2+⋅⋅⋅+(yn−zn)2)≥(x1−y1)2+2(x1−y1)(y1−z1)+(y1−z1)2+⋅⋅⋅+(xn−yn)2+2(xn−yn)(yn−zn)+(yn−zn)2=(x1−z1)2+⋅⋅⋅+(xn−zn)2=(d(x,z))2(d(x,y)+d(y,z))^2=(\sqrt{(x_1-y_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2}+\sqrt{(y_1-z_1)^2+\cdot\cdot\cdot+(y_n-z_n)^2})^2=(x_1-y_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2+(y_1-z_1)^2+\cdot\cdot\cdot+(y_n-z_n)^2+2\sqrt{((x_1-y_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2)((y_1-z_1)^2+\cdot\cdot\cdot+(y_n-z_n)^2)}\ge(x_1-y_1)^2+2(x_1-y_1)(y_1-z_1)+(y_1-z_1)^2+\cdot\cdot\cdot+(x_n-y_n)^2+2(x_n-y_n)(y_n-z_n)+(y_n-z_n)^2=(x_1-z_1)^2+\cdot\cdot\cdot+(x_n-z_n)^2=(d(x,z))^2(d(x,y)+d(y,z))2=((x1−y1)2+⋅⋅⋅+(xn−yn)2+(y1−z1)2+⋅⋅⋅+(yn−zn)2)2=(x1−y1)2+⋅⋅⋅+(xn−yn)2+(y1−z1)2+⋅⋅⋅+(yn−zn)2+2((x1−y1)2+⋅⋅⋅+(xn−yn)2)((y1−z1)2+⋅⋅⋅+(yn−zn)2)≥(x1−y1)2+2(x1−y1)(y1−z1)+(y1−z1)2+⋅⋅⋅+(xn−yn)2+2(xn−yn)(yn−zn)+(yn−zn)2=(x1−z1)2+⋅⋅⋅+(xn−zn)2=(d(x,z))2,其中不等号是来源于Cauchy−SchwarzCauchy-SchwarzCauchy−Schwarz不等式。
A5)A5)A5)(重要)给定距离空间(X,d),Y⊂X(X,d),Y⊂X(X,d),Y⊂X是子集。如果对任意的x∈Xx∈Xx∈X 和任意的ε>0ε>0ε>0,都存在y∈Yy∈Yy∈Y,使得d(y,x)<εd(y, x)<εd(y,x)<ε,我们就称YYY在XXX中是稠密的。证明,有理数在R\RR中(距离函数由两个数的差的绝对值定义)是稠密的。
证明:等价的命题已在过去证明过。
A6)A6)A6) 对于(x,y)∈R2(x,y)∈\R^2(x,y)∈R2,如果它的坐标xxx和yyy都是有理数,我们就称这个点是有理点。证明,(R2,d)(\R^2, d)(R2,d)中的有理点是稠密的。
证明:注意到这里的距离函数ddd定义为d((a1,a2),(b1,b2))=(a1−b1)2+(a2−b2)2d((a_1,a_2),(b_1,b_2))=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}d((a1,a2),(b1,b2))=(a1−b1)2+(a2−b2)2。设(x,y)∈R2(x,y)\in\R^2(x,y)∈R2,设ε>0ε>0ε>0,根据有理数在R\RR中的稠密性,存在x′,y′∈Q,∣x−x′∣<ε2,∣y−y′∣<ε2x',y'\in\mathbb{Q},|x-x'|<\frac{ε}{\sqrt{2}},|y-y'|<\frac{ε}{\sqrt{2}}x′,y′∈Q,∣x−x′∣<2ε,∣y−y′∣<2ε,显然d((x′,y′),(x,y))<εd((x',y'),(x,y))<εd((x′,y′),(x,y))<ε,得证。
A7)A7)A7) 证明,假定域公理(F)(F)(F)和序公理(O)(O)(O),确界原理可以推出 ArchimedesArchimedesArchimedes公理(A)(A)(A)。
证明:设a>0,b∈Ra>0,b\in\Ra>0,b∈R,想要证明存在k∈Z,ka>bk\in\Z,ka>bk∈Z,ka>b。不妨设b>0b>0b>0,定义K={k∈Z∣ka≤b}K=\{k\in\Z|ka\le b\}K={k∈Z∣ka≤b},显然对于每个k∈K,k≤ba−1k\in K,k\le ba^{-1}k∈K,k≤ba−1,因此KKK有上界从而有上确界supK\sup KsupK,令k0=supK=[ba−1]k_0=\sup K=[ba^{-1}]k0=supK=[ba−1],这里[⋅][\cdot][⋅]表示下取整函数。从而k0+1∉Kk_0+1\notin Kk0+1∈/K即(k0+1)a>b(k_0+1)a>b(k0+1)a>b,证毕。
A8)A8)A8) (无理数的存在性)令X={x∈R∣x2≤2}X=\{x\in\R|x^2\le 2\}X={x∈R∣x2≤2},这是一个有界的集合。令2=supX\sqrt{2}=\sup X2=supX。证明,2\sqrt{2}2不是有理数。
证明:已经在过去证明过。
A9)A9)A9) 证明,每个开区间总包含无穷多个无理数。
证明:设开区间(l,r)(l,r)(l,r),取xn=l+r−l2n⋅2x_n=l+\frac{r-l}{2^n}\cdot\sqrt{2}xn=l+2nr−l⋅2,显然xnx_nxn不是有理数并且l<xn<rl<x_n<rl<xn<r。注意到{xn}\{x_n\}{xn}单调递减从而互不重复,从而开区间内包含了无穷多个无理数。
B:B:B:可数与不可数
令N\NN表示自然数的集合(包括000)。XXX是一个集合,如果存在单射f:X→Nf:X\rightarrow\Nf:X→N,我们就称XXX是可数的。如果XXX不是可数的,我们就称它是不可数的。
B1)B1)B1) 证明,有限集是可数的。
证明:执行以下步骤:(设X1=XX_1=XX1=X)
第jjj步:当Xj=∅X_j=\emptyXj=∅时结束,否则从XjX_jXj中取一个元素xjx_jxj,定义f(xj)=jf(x_j)=jf(xj)=j然后定义Xj+1=Xj−{xj}X_{j+1}=X_j-\{x_j\}Xj+1=Xj−{xj}
显然上述步骤会于有限步内结束因为XXX是有限集,且fff显然是一个单射因为每一次赋的函数值不同。
B2)B2)B2) 证明,可数集合的子集是可数的。
证明:设XXX是一个可数集而Y⊂XY\sub XY⊂X,那么f∣Y:Y→N,y↦f(y)f|_Y:Y\rightarrow\N,y\mapsto f(y)f∣Y:Y→N,y↦f(y)是fff在YYY上的限制,这显然还是个单射。
B3)B3)B3) 证明,如果XXX是可数集,那么我们总可以将XXX写成X={x1,x2,x3,⋯ }X=\{x_1,x_2,x_3,\cdots\}X={x1,x2,x3,⋯}(即可以把XXX中的元素用自然数来标号)。(我们可以从一开始一个一个地数下去把这些元素都罗列出来,所以叫做可数集)
证明:显然N\NN的子集都可数(考虑恒等映射即可),从而f(X)={n∈N∣存在x∈X,使得f(x)=n}f(X)=\{n\in\N|存在x\in X,使得f(x)=n\}f(X)={n∈N∣存在x∈X,使得f(x)=n}是可数的。自然数集有下界从而其子集也有下界,因而f(X)f(X)f(X)及其任意子集的最小元都存在。执行以下步骤:(设Y1=f(X)Y_1=f(X)Y1=f(X))
第jjj步,取YjY_jYj的最小元yjy_jyj,定义g(yj)=jg(y_j)=jg(yj)=j,然后定义Yj+1=Yj−{yj}Y_{j+1}=Y_j-\{y_j\}Yj+1=Yj−{yj}。
那么f(X)f(X)f(X)中的任意元素都被赋了一个相应于函数ggg的函数值(因为第jjj小的元素一定在第jjj步被取出),即构造了g:f(X)→{1,2,3,⋯ }g:f(X)\rightarrow \{1,2,3,\cdots\}g:f(X)→{1,2,3,⋯},从而f:X→f(X)f:X\rightarrow f(X)f:X→f(X)和g:f(X)→g(f(X))g:f(X)\rightarrow g(f(X))g:f(X)→g(f(X))都是双射,从而g∘f:X→g(f(X))g\circ f:X\rightarrow g(f(X))g∘f:X→g(f(X))是双射因而存在着逆映射τ:g(f(X))→X\tau:g(f(X))\rightarrow Xτ:g(f(X))→X。据此定义xj=τ(j)x_j=\tau(j)xj=τ(j)即可。
B5)B5)B5) 证明,可数个可数集的并也是可数集,也就是说,如果X1,X2,⋯ ,Xn,⋯X_1,X_2,\cdots,X_n,\cdotsX1,X2,⋯,Xn,⋯都是可数集,那么它们的并集⋃n∈NXn\bigcup_{n\in\N}X_n⋃n∈NXn也是可数集。
证明:如下列出各集合并按照箭头顺序从小到大标号即可。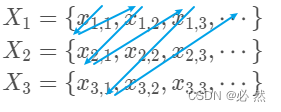
B4)B4)B4) 证明,有理数Q\mathbb{Q}Q是可数集。
证明:定义Xj={nj∣n∈N}X_j=\{\frac{n}{j}|n\in\N\}Xj={jn∣n∈N}显然可数,那么Q≥0=⋃n∈NXn\mathbb{Q}_{\ge0}=\bigcup_{n\in\N}X_nQ≥0=⋃n∈NXn也可数,同理Q≤0\mathbb{Q}_{\le0}Q≤0也可数,从而Q\mathbb{Q}Q可数。
B6)B6)B6) 证明,XXX是可数的,映射f:X→Yf:X\rightarrow Yf:X→Y是满射。证明,YYY是可数的。
证明:这是因为满射可以诱导出一个逆向的单射g:Y→Xg:Y\rightarrow Xg:Y→X,即对任意的y∈Yy\in Yy∈Y,显然{x∈X∣f(x)=y}\{x\in X|f(x)=y\}{x∈X∣f(x)=y}非空,从中任取一个定义为g(y)g(y)g(y),此时ggg是单射,因为假设g(a)=g(b)g(a)=g(b)g(a)=g(b),就有f(g(a))=f(g(b))f(g(a))=f(g(b))f(g(a))=f(g(b)),而根据定义f(g(a))=a,f(g(b))=bf(g(a))=a,f(g(b))=bf(g(a))=a,f(g(b))=b,从而a=ba=ba=b。而XXX可数,从而存在单射h:X→Nh:X\rightarrow\Nh:X→N,那么h∘g:Y→Nh\circ g:Y\rightarrow\Nh∘g:Y→N也是单射,得证。
B7)B7)B7) 按照以下步骤证明R\RR是不可数的:
B7−1)B7-1)B7−1) J⊂RJ\sub\RJ⊂R是闭区间并且它的长度∣J∣>0|J|>0∣J∣>0。证明,对任意的x∈Rx\in\Rx∈R,总存在闭区间III,使得I⊂J,∣I∣>0,x∉II\sub J,|I|>0,x\notin II⊂J,∣I∣>0,x∈/I。
证明:不妨设x∈J=[l,r]x\in J=[l,r]x∈J=[l,r]且x≠lx\neq lx=l,取I=[l,x+l2]I=[l,\frac{x+l}{2}]I=[l,2x+l]即符合要求。
B7−2)B7-2)B7−2) 证明,如果{x1,x2,⋯ }\{x_1,x_2,\cdots\}{x1,x2,⋯}是R\RR的一个可数子集,那么存在闭区间套I1⊃I2⊃⋯I_1\supset I_2\supset\cdotsI1⊃I2⊃⋯,使得对任意的n,xn∉Inn,x_n\notin I_nn,xn∈/In。
证明:在R−{x1}\R-\{x_1\}R−{x1}中取一个闭区间定义为I1I_1I1。对于InI_nIn,取In+1⊂InI_{n+1}\sub I_nIn+1⊂In,使得xn+1∉In+1x_{n+1}\notin I_{n+1}xn+1∈/In+1,B7−1)B7-1)B7−1)保证这样的In+1I_{n+1}In+1是存在的。从而得到区间套。
B7−3)B7-3)B7−3) 证明,R\RR不可数。
证明:用反证法,假设R\RR可数,那么有R={x1,x2,⋯ }\R=\{x_1,x_2,\cdots\}R={x1,x2,⋯},由B7−2)B7-2)B7−2)得存在闭区间套I1⊃I2⊃⋯I_1\supset I_2\supset\cdotsI1⊃I2⊃⋯,使得对任意的n,xn∉Inn,x_n\notin I_nn,xn∈/In,从而对任意的xn∈Rx_n\in\Rxn∈R,xn∉⋂n>0Inx_n\notin\bigcap_{n>0}I_nxn∈/⋂n>0In因为xn∉Inx_n\notin I_nxn∈/In,因而⋂n>0In=∅\bigcap_{n>0}I_n=\empty⋂n>0In=∅,与区间套公理矛盾。从而R\RR不可数。
B8)B8)B8) 证明,如果XXX是不可数集,AAA是XXX的可数子集,那么X−AX-AX−A是不可数的。
证明:否则X=(X−A)∪AX=(X-A)\cup AX=(X−A)∪A可数。
B9)B9)B9) 证明,任意的长度不为000的区间(无论开或闭)都是不可数的。
证明:用反证法,假设区间(l,r)(l,r)(l,r)是可数的,在这个区间内部可以取出一个区间套I1⊃I2⊃⋯I_1\supset I_2\supset\cdotsI1⊃I2⊃⋯使得⋂n>0In\bigcap_{n>0}I_n⋂n>0In不包含任意的(l,r)(l,r)(l,r)中的元素,然而由于这个区间套取自(l,r)(l,r)(l,r)即I1⊂(l,r)I_1\sub(l,r)I1⊂(l,r)因此⋂n>0In\bigcap_{n>0}I_n⋂n>0In也不包含R−(l,r)\R-(l,r)R−(l,r)中的元素,从而⋂n>0In=∅\bigcap_{n>0}I_n=\empty⋂n>0In=∅,与区间套公理矛盾。因此(l,r)(l,r)(l,r)不可数。闭区间的情形是类似的。
B10)B10)B10) 证明,复数C\mathbb{C}C是不可数的。
证明:由于可数集的子集可数,可知子集不可数的集合不可数,由于R⊂C\R\sub\mathbb{C}R⊂C可知C\mathbb{C}C不可数。
B11)B11)B11) 假设I\mathcal{I}I是R\RR上某些开区间组成的集合,它满足如下性质:对任意的I,J∈I,I≠JI,J\in\mathcal{I},I\neq JI,J∈I,I=J,那么它们的交集是空集,即I∩J=∅I\cap J=\emptyI∩J=∅。证明,I\mathcal{I}I是可数集。
证明:由于任意开区间总包含无限个有理数,定义f:I→Qf:\mathcal{I}\rightarrow\mathbb{Q}f:I→Q,对于I∈II\in\mathcal{I}I∈I,定义f(I)f(I)f(I)为III中某个有理数。那么fff是一个单射,因为假设f(I)=f(J)=p∈Qf(I)=f(J)=p\in\mathbb{Q}f(I)=f(J)=p∈Q,那么p∈I∩Jp\in I\cap Jp∈I∩J即I∩J≠∅I\cap J\neq\emptyI∩J=∅从而I=JI=JI=J(否则两个开区间交集为空)。由于有理数是可数的即存在单射g:Q→Ng:\mathbb{Q}\rightarrow\Ng:Q→N,因而g∘f:I→Ng\circ f:\mathcal{I}\rightarrow\Ng∘f:I→N是单射,因而I\mathcal{I}I可数。
C:C:C: Schroeder−BernsteinSchroeder-BernsteinSchroeder−Bernstein定理
假设XXX和YYY是两个集合,映射f:X→Yf:X\rightarrow Yf:X→Y和g:Y→Xg:Y\rightarrow Xg:Y→X都是单射。我们令X′=X−g(Y)。X'=X-g(Y)。X′=X−g(Y)。
C1)C1)C1) 如果XXX是有限集,证明,存在φ:X→Y\varphi:X\rightarrow Yφ:X→Y,使得φ\varphiφ是双射。
证明:设X={x1,⋯ ,xn},Y={y1,⋯ ,ym}X=\{x_1,\cdots,x_n\},Y=\{y_1,\cdots,y_m\}X={x1,⋯,xn},Y={y1,⋯,ym}。由于存在由XXX到YYY的单射,有n≤mn\le mn≤m,同理n≥mn\ge mn≥m,从而n=mn=mn=m。定义φ:X→Y,xj↦yj\varphi:X\rightarrow Y,x_j\mapsto y_jφ:X→Y,xj↦yj符合要求。
C2)C2)C2) 如果XXX是可数集,证明,存在φ:X→Y\varphi:X\rightarrow Yφ:X→Y,使得φ\varphiφ是双射。
证明:设XXX是有限集,由于存在YYY到XXX的单射,YYY也必为有限集(否则取{y1,⋯ ,yn+1}⊂Y\{y_1,\cdots,y_{n+1}\}\sub Y{y1,⋯,yn+1}⊂Y,其中nnn是XXX的元素个数,从而{g(y1),⋯ ,g(yn+1)}⊂X\{g(y_1),\cdots,g(y_{n+1})\}\sub X{g(y1),⋯,g(yn+1)}⊂X,与XXX有nnn个元素矛盾),而有限集的情形已经证明过了。不妨设X,YX,YX,Y都是无限可数集。对于无限可数集X={x1,x2,⋯ }X=\{x_1,x_2,\cdots\}X={x1,x2,⋯},可以定义双射h:X→N,xj↦j−1h:X\rightarrow\N,x_j\mapsto j-1h:X→N,xj↦j−1。显然hhh是一个双射。同理存在双射i:Y→Ni:Y\rightarrow\Ni:Y→N,因此i−1∘h:X→Yi^{-1}\circ h:X\rightarrow Yi−1∘h:X→Y是双射。
从现在开始,对XXX不加任何的限制。我们令h:X→Xh:X\rightarrow Xh:X→X是复合映射h=g∘fh=g\circ fh=g∘f:

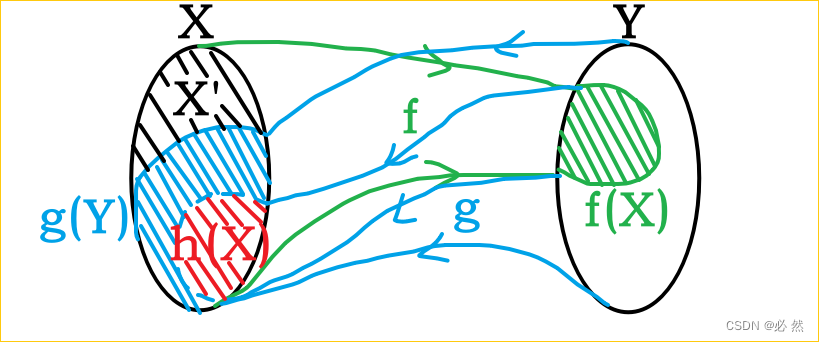
我们期望结合fff与ggg的映射关系来构造这个双射。即找到一个XXX的划分和YYY的划分,让fff和ggg分别在对应的划分上成为双射,从而得到X,YX,YX,Y之间的一个双射。
C3)C3)C3) 考虑XXX的子集的集合F={A⊂X∣X′∪h(A)⊂A}\mathcal{F}=\{A\sub X|X'\cup h(A)\sub A\}F={A⊂X∣X′∪h(A)⊂A}。证明,F\mathcal{F}F非空。
证明:X′,h(X)⊂XX',h(X)\sub XX′,h(X)⊂X从而X∈FX\in\mathcal{F}X∈F。
C4)C4)C4) 证明,如果A∈FA\in\mathcal{F}A∈F,那么X′∪h(A)∈FX'\cup h(A)\in\mathcal{F}X′∪h(A)∈F。
证明:先证若A⊂BA\sub BA⊂B,那么A∪C⊂B∪CA\cup C\sub B\cup CA∪C⊂B∪C。设x∈A∪Cx\in A\cup Cx∈A∪C即x∈Ax\in Ax∈A或x∈Cx\in Cx∈C则x∈Bx\in Bx∈B或x∈Cx\in Cx∈C那么x∈B∪Cx\in B\cup Cx∈B∪C,得证。
由A∈FA\in\mathcal{F}A∈F有X′∪h(A)⊂AX'\cup h(A)\sub AX′∪h(A)⊂A,h(X′∪h(A))⊂h(A)h(X'\cup h(A))\sub h(A)h(X′∪h(A))⊂h(A)从而X′∪h(X′∪h(A))⊂X′∪h(A)X'\cup h(X'\cup h(A))\sub X'\cup h(A)X′∪h(X′∪h(A))⊂X′∪h(A),根据定义有X′∪h(A)∈FX'\cup h(A)\in\mathcal{F}X′∪h(A)∈F。
C5)C5)C5) 我们定义
A0=⋂A∈FA={x∈X∣对任意的A∈F,都有x∈A} A_0=\bigcap_{A\in\mathcal{F}}A=\{x\in X|对任意的A\in\mathcal{F},都有x\in A\} A0=A∈F⋂A={x∈X∣对任意的A∈F,都有x∈A}
证明,A0∈FA_0\in\mathcal{F}A0∈F。
证明:只需证明X′∪h(A0)⊂A0X'\cup h(A_0)\sub A_0X′∪h(A0)⊂A0。任取A′∈FA'\in\mathcal{F}A′∈F,注意到h(A0)=h(⋂A∈FA)⊂h(A′)h(A_0)=h(\bigcap_{A\in\mathcal{F}}A)\sub h(A')h(A0)=h(⋂A∈FA)⊂h(A′)从而X′∪h(A0)⊂X′∪h(A′)⊂A′X'\cup h(A_0)\sub X'\cup h(A')\sub A'X′∪h(A0)⊂X′∪h(A′)⊂A′,从而X′∪h(A0)⊂⋂A∈FA=A0X'\cup h(A_0)\sub \bigcap_{A\in\mathcal{F}}A=A_0X′∪h(A0)⊂⋂A∈FA=A0,得证。
C6)C6)C6) 证明,X′∪h(A0)=A0X'\cup h(A_0)=A_0X′∪h(A0)=A0。
证明:由于A0∈FA_0\in\mathcal{F}A0∈F可知X′∪h(A0)⊂A0X'\cup h(A_0)\sub A_0X′∪h(A0)⊂A0。由C4)C4)C4)知X′∪h(A0)∈FX'\cup h(A_0)\in\mathcal{F}X′∪h(A0)∈F,因此A0=⋂A∈FA⊂X′∪h(A0)A_0=\bigcap_{A\in\mathcal{F}}A\sub X'\cup h(A_0)A0=⋂A∈FA⊂X′∪h(A0),从而X′∪h(A0)=A0X'\cup h(A_0)=A_0X′∪h(A0)=A0。
C7)C7)C7) 令B0=X−A0B_0=X-A_0B0=X−A0。证明,f(A0)∩g−1(B0)=∅f(A_0)\cap g^{-1}(B_0)=\emptyf(A0)∩g−1(B0)=∅并且f(A0)∪g−1(B0)=Yf(A_0)\cup g^{-1}(B_0)=Yf(A0)∪g−1(B0)=Y。
证明:设y∈Yy\in Yy∈Y。设y∈f(A0)y\in f(A_0)y∈f(A0)即存在x∈A0x\in A_0x∈A0使得y=f(x)y=f(x)y=f(x),考虑那么g(y)=g(f(x))=h(x)∈h(A0)⊂X′∪h(A0)=A0g(y)=g(f(x))=h(x)\in h(A_0)\sub X'\cup h(A_0)=A_0g(y)=g(f(x))=h(x)∈h(A0)⊂X′∪h(A0)=A0因而g(y)∉B0g(y)\notin B_0g(y)∈/B0从而y∉g−1(B0)y\notin g^{-1}(B_0)y∈/g−1(B0),因此f(A0)∩g−1(B0)=∅f(A_0)\cap g^{-1}(B_0)=\emptyf(A0)∩g−1(B0)=∅;另一方面,假设y∉g−1(B0)y\notin g^{-1}(B_0)y∈/g−1(B0)即g(y)∈A0=X′∪h(A0)g(y)\in A_0=X'\cup h(A_0)g(y)∈A0=X′∪h(A0),由于X′=X−g(Y)X'=X-g(Y)X′=X−g(Y)从而g(y)∉X′g(y)\notin X'g(y)∈/X′从而g(y)∈h(A0)g(y)\in h(A_0)g(y)∈h(A0)即存在x∈A0x\in A_0x∈A0使得g(y)=g(f(x))g(y)=g(f(x))g(y)=g(f(x)),由于ggg是单射有y=f(x)y=f(x)y=f(x)即y∈f(A0)y\in f(A_0)y∈f(A0),证毕。
注意到此处证明了对所有的x∈Ux\in Ux∈U:1)1)1)若x∈Ax\in Ax∈A则x∉Bx\notin Bx∈/B,这就证明了A∩B=∅A\cap B=\emptyA∩B=∅;2)2)2)若x∉Bx\notin Bx∈/B则x∈Ax\in Ax∈A,这就证明了x∈Bx\in Bx∈B或x∈Ax\in Ax∈A必居其一,即A∪B=UA\cup B=UA∪B=U。
C8)C8)C8) 我们定义映射φ:X→Y\varphi:X\rightarrow Yφ:X→Y:对于x∈Xx\in Xx∈X,我们要求
若x∈A0,则φ(x)=f(x)若x∈B0,则φ(x)=g−1(x) 若x\in A_0,则\varphi(x)=f(x)\\ 若x\in B_0,则\varphi(x)=g^{-1}(x) 若x∈A0,则φ(x)=f(x)若x∈B0,则φ(x)=g−1(x)
证明,这是双射。
证明:先证明g−1g^{-1}g−1在B0B_0B0上是存在的,也即g:g−1(B0)→B0g:g^{-1}(B_0)\rightarrow B_0g:g−1(B0)→B0是双射。由于g:Y→Xg:Y\rightarrow Xg:Y→X是单射从而g∣g−1(B0):g−1(B0)→Xg|_{g^{-1}(B_0)}:g^{-1}(B_0)\rightarrow Xg∣g−1(B0):g−1(B0)→X也是单射,那么g:g−1(B0)→B0g:g^{-1}(B_0)\rightarrow B_0g:g−1(B0)→B0也是单射;另一方面,根据g−1(B0)g^{-1}(B_0)g−1(B0)的定义即g−1(B0)={y∈Y∣g(y)∈B0}g^{-1}(B_0)=\{y\in Y|g(y)\in B_0\}g−1(B0)={y∈Y∣g(y)∈B0},对任意的b∈B0b\in B_0b∈B0,由于B0=X−A0=X−X′∪h(A0)B_0=X-A_0=X-X'\cup h(A_0)B0=X−A0=X−X′∪h(A0),有B0⊂g(Y)B_0\sub g(Y)B0⊂g(Y),从而存在y∈g−1(B0)y\in g^{-1}(B_0)y∈g−1(B0)使得g(y)=bg(y)=bg(y)=b。从而g:g−1(B0)→B0g:g^{-1}(B_0)\rightarrow B_0g:g−1(B0)→B0是双射从而在这个局部g−1g^{-1}g−1存在。
现在证明φ\varphiφ是双射。这是因为A0,B0A_0,B_0A0,B0是XXX的一个划分,而f(A0),g−1(B0)f(A_0),g^{-1}(B_0)f(A0),g−1(B0)是YYY的一个划分,而f:A0→f(A0),g−1:B0→f−1(B0)f:A_0\rightarrow f(A_0),g^{-1}:B_0\rightarrow f^{-1}(B_0)f:A0→f(A0),g−1:B0→f−1(B0)都是双射,从而φ\varphiφ是一个双射。形式证明的细节容易补充。
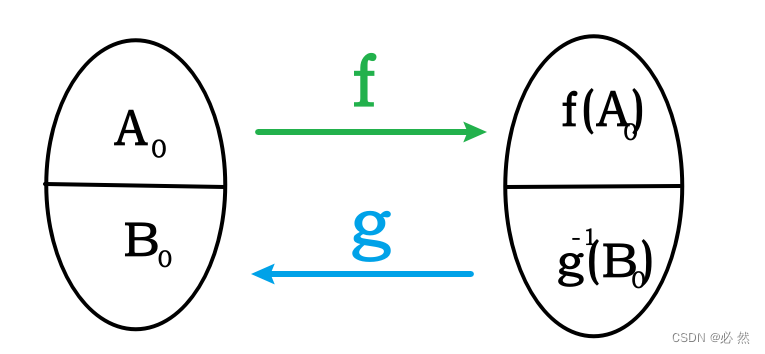
根据上述,我们证明了
定理(Schroeder−BernsteinSchroeder-BernsteinSchroeder−Bernstein)如果有单射f:X→Yf:X\rightarrow Yf:X→Y和单射g:Y→Xg:Y\rightarrow Xg:Y→X,那么存在着两个集合之间的双射φ:X→Y\varphi:X\rightarrow Yφ:X→Y。
D:D:D:DedekindDedekindDedekind分割的细节
(略)
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容








所有评论(0)