提示：暂无提示

---

前言

当问题不能被拆分求解的时候，可以使用搜索技术。与分治算法、动态规划算法、贪心算法不同，搜索技术不需要划分子问题，也不需要递归求解子问题。所谓搜索，就是列举可能的情况，继而在这些情况中选择符合要求的结果作为问题的解。但搜索与暴力穷举不同的是，穷举是无目的性的，列举所有可能的情况直到选出符合条件的结果。而搜索是一种有目的的穷举，利用了状态空间模型，将问题转化为状态空间图，设计特定的遍历算法在状态空间中寻求问题的解。

---

一、无信息搜索

无信息的搜索盲目性较强，最基本的就是DFS和BFS两种经典遍历算法

1、DFS（深度优先搜索）

DFS利用栈或者递归函数来实现，形象表述为“一条路走到黑”。
这个算法会尽可能深地搜索树的分支。当节点v的所在边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

以下是深度优先搜索的基本步骤：

1、从一个未访问的顶点开始。
2、选择一条从该顶点出发的未探索过的边，然后沿这条边走到下一个顶点。
3、如果该顶点还有未探索过的边，则选择其中一条继续深度优先搜索。
4、如果没有未探索过的边，则回溯到前一个顶点，直到找到还有未探索过的边的顶点。
5、重复以上步骤，直到所有顶点都被访问过。

2、BFS（广度优先搜索）

BFS实现利用的是队列，形象表述为“一层一层走”。
广度优先搜索会首先访问离根节点（或任意选定的起始节点）最近的节点，然后逐层向外扩展，直到访问到所有节点。

以下是广度优先搜索的基本步骤：

从一个起始节点开始，将其标记为已访问，并将其加入到一个队列中。
当队列不为空时，执行以下步骤：
a. 从队列中取出一个节点。
b. 访问该节点的所有未访问过的邻居节点，并将它们标记为已访问，然后加入到队列中。
重复步骤2，直到队列为空，即所有可达节点都已被访问。

3、比较

深度优先搜索更可能找到一个可行解，占内存少，但速度慢，不确定性强；
广度优先搜索占内存多，但速度快，当结点到跟结点的费用（耗散值）和结点的深度成正比时，能较快得到最优解。
无论是DFS还是BFS都是简单的遍历算法，一定程度上体现了遍历的“有目的性”，但是表现出来的目的性不强，残留了较多原始人“枚举”的气息，导致在很多具体问题的求解过程中显得臃肿乏力。

二、有信息搜索

为了为提高搜索的效率，可在遍历状态空间时加入优化技术

1.搜索前

根据条件进行筛选，降低搜索规模

2.剪枝策略

（1）根据(问题的)约束条件，避免不必要的搜索
（2）减少对搜索过程里中间解的重复计算

3、启发式策略

加速朝目标状态逼近的速度

三、爬山算法

基本思想

爬山法本质上是局部择优的贪心搜索算法，是运用了贪心策略来优化的深度优先算法。贪心性表现在选择的侧重性上，通过启发式评价函数来确定走哪条路。
算法通过评估当下即将做出的选择中，哪一种看起来是最优的（使得状态更优），从而做出选择，如果即将做出的选择中没有好的选择的（就是不论怎么选状态都会变差时）或者已经到达了最优解时，该算法停止。

举例

游戏开始后，玩家随机处于某一个状态，每次给出若干个选项，如+1、+2、-3、+4，选择后就能得到相应的金币。那么怎么样使得我们获得的金币是最多的呢？由于未来是不可预测的，所以我们总是做出当下最好的选择，即选择+4，因为这个对于我们来说是当下最优的选择。按照这种方式一直选，直到我们遇到的选项全是负的，如-1、-2、-3、-4时，我们不做选择，停止游戏，及时止损。这种就是贪心策略，基于这种策略，在平均运气的条件下，我们能保证获得的金币不会很低。
但是这种策略能保证我们获得的金币是最多的吗？显然不一定，因为人们无法预测未来，实际上当下的贪婪并不能保证成为最后的赢家，每一次选择都是一次博弈，虽然我们第一次选择的是最多的+4，但是有可能以后出现的都是+1、+2这些不大的数，甚至很快之后就出现全为负数的选择。而第一次选+1后，也有可能突然冒出个+100的选项，从而使得金币数多于第一次选择+4的情况。贪心的局限性固然存在，但是生而为人，我们没有理由抱着逆反的心态专门挑金币少的来选，以期望下一次会得到命运的眷顾。我们能做的，就是做出当下最好的选择，尽人事，听天命。这样的话，我们虽然无法保证我们的人生是最优解，但是至少，我们有自信的说出我们是局部最优。

步骤

一言以蔽之，就是“只往高处走”
算法每次从当前的节点开始，与周围的邻接点进行比较：

若当前节点是使得状态最优的，即邻接节点都使得状态变差，那么返回当前节点，作为最大值（已经到达了顶点）
若当前节点不是使得状态最优的，就用最高的邻接点替换当前节点，从而实现向山峰的高处攀爬的目的
如此循环往复，直到达到最高点为止。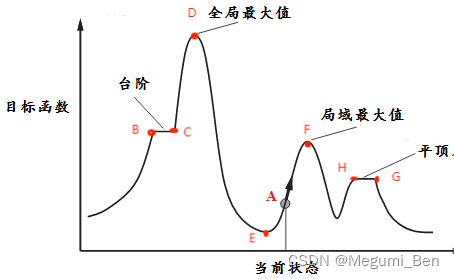

处在当前状态A时，假定我们有两种选择，一种是向下走1步（左边），一种是向上走2步（右边），基于贪心策略，我们选择最大的，即向上走两步，然后我们到达了极值点（小山峰），此时无论我们做出何种选择，我们今后都是向下走的，此时我们就认为到达了顶峰，这个就是局部最优解。实际上，当我们开始时选择向下走1步（即左边）时，虽然暂时走到了低谷，但是后面这个方向会出现一个向上6步的，从而到达真正的最高点（最优解）。我们想让评估函数尽可能的大，但是实际上我们的贪心策略无法保证我们找到最优解，很多情况下我们找到的只是极值点（局部最优）而不是最值点（最优），而这就是爬山法的局限性。

优劣

优势：当不清楚正解、或者状态维度多时适用；对单峰函数可行
缺点：
1、容易陷入局部最优解
2、容易陷入死循环：
回到上图的“台阶”部分。假定我们从图片最左边开始走，一直走到了半山腰的台阶，此时我们的选项里，没有使得状态函数增加的选择，最好的情况也使得做出选择后的状态和现在一样而不能变的更好。在这种“平坦”区域，我们是接受这种原地踏步的选择还是直接结束呢？显然，一般人都会选择继续。至少，当下的选择对于我们而言，即使没有对状态的改善，但至少没有发生损失。因此，我们继续往前走，从B点到C点以后，就又出现了使得状态更优的选择，之后我们来到了D，得出了最优解，所以这种接受平坦状态的决策更有利于找到最优解。
但是接受平坦状态也有弊端，高原问题就是其中之一。假使我处在右边平顶区域中的H点，接受的最好状态就是平坦状态，过渡到G点，而对于G点而言，最好的状态也只能是平坦状态H点。至此，求解过程就会在这两个选择中反复横跳，陷入死循环。

尾话

爬山算法是贪心的深度优先搜索算法，本质上是梯度下降，在8皇后、8数码等问题中有一席之地。与此同时，爬山法的弊端是容易陷入局部最优解或者进入死循环。为了避免这些弊端，我们又对爬山算法进行改进，这就是后来的随机重启算法和模拟退火算法，详情见下一节。感谢阅读