广度优先搜索(Breadth First Search)

广度优先搜索遍历类似于树的按层序遍历



第一个结点A入队，检查与结点A相连的结点B和结点F，结点A已经处理完，将结点A出队，
检查与结点B相连的结点C、结点I、结点G，结点B已经处理完，将结点B出队，
检查与结点F相连的结点G和结点E，结点G已经入队，将结点E入队，结点F已经处理完，将结点F出队……以此类推

1.广度优先搜索遍历连通图

void BFS(Graph G, int v){
	cout << v;	//输入某个顶点在一维数组中的下标
	visited[v]=true;	//访问第v个顶点，并置访问标志数组相应值为true
	InitQueue(Q);	//初始化队列
	EnQueue(Q,v);	//将下标为v的顶点加入队列
	while(!QueueEmpty(Q)){	//队列非空
		DeQueue(Q,u);	//队头顶点出队并将其置为u
		for(w=FirstAdjvex(G,u); w>=0; w=NextAdjVex(G,u,w))	//这里的FirstAdjVex和NextAdjVex没有具体展开。如果图的存储结构不同，这两个的实现方法不同
		//依次检查u的所有邻接点w
		//FirstAdjVex(G,u)表示u的第一个邻接点
		//w>=0表示存在邻接点
		//NextAdjVex(G,u,w)表示u的相对于w的下一个邻接点
			if(!visited[w]){	//w为u的尚未访问的邻接顶点
				cout << w;	//输出已访问过的顶点下标
				visited[w]=true;	//将访问过的顶点标记为true
				EnQueue(Q,w);	//下标为w的顶点进队
			}
	}
}

若是遍历非连通图，上述遍历过程执行完后(只是遍历完一个连通分量)，一定还有顶点未被访问(从另一个连通分量的某顶点开始访问)，需从图中另选一个未被访问的顶点作为起始点，重复上述过程。

2.广度优先搜索遍历以结构为邻接矩阵的图

无向图

有向图

邻接矩阵存储表示

#define MaxInt 32767	//表示极大值,即无穷大
#define MVNum 100		//最大顶点数
typedef char VerTexType;	//顶点的数据类型为字符型
typedef int ArcType;	//边的权值类型为整型
typedef struct{
	VerTexType vexs[MVNum];	//顶点表
	ArcType arcs[MVNum][MVNum];	//边表（邻接矩阵）
	int vexnum,arcnum;	//图的当前顶点数和边数
}AMGraph;

邻接矩阵的广度遍历

void BFSTraverse(AMGraph G){
	for(int i=0; i<G.vexnum; ++i)	//初始化标志数组
		visited[i]=false;	//初值设为false，即未被访问过
	InitQueue(Q);	//初始化队列
	for(i=0; i<G.vexnum; ++i){	//遍历邻接矩阵的行
		if(!visited[i]){	//行标为i对应的顶点未被访问，比如i=0,则对应V_0
			visited[i]=true;
			cout << G.vexs[i];	//输出邻接矩阵中行标对应的顶点，比如i=0,则对应V_0
			EnQueue(Q,i);	//行标为i对应的顶点入队
			while(!QueueEmpty(Q)){	//队列非空
				DeQueue(Q,i);	//行标为i对应的顶点出队/队头顶点出队
				for(int j=0; j<G.vexnum; ++j){	//遍历邻接矩阵的列
					if(G.arcs[i][j] == 1 && !visited[j]){	//!visited[j]矩阵中列标对应的顶点未被访问过
						visited[j]=true;
						cout << G.vexs[j];	//输出列标j对应的顶点
						EnQueue(Q,j); //列标j对应的顶点入列
					}
				}
			}
		}
	}
}

3.广度优先搜索遍历以结构为邻接表的图

无向图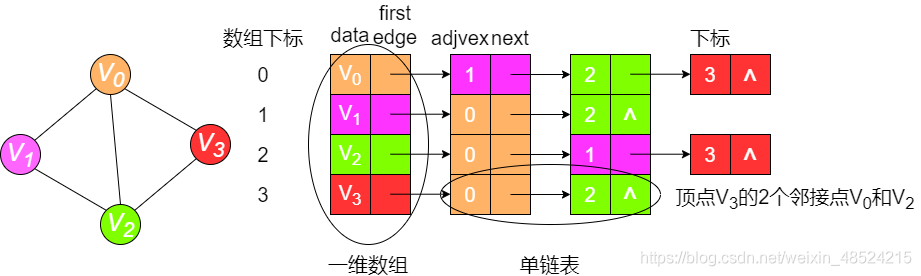


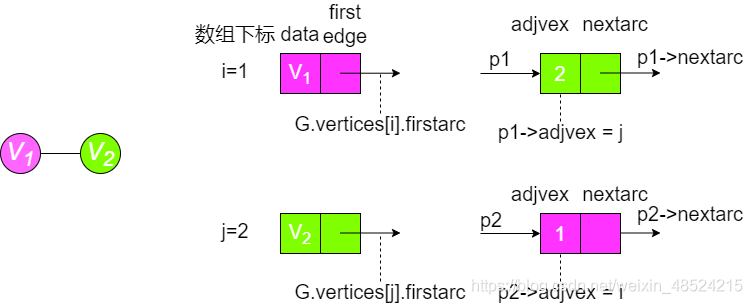
有向图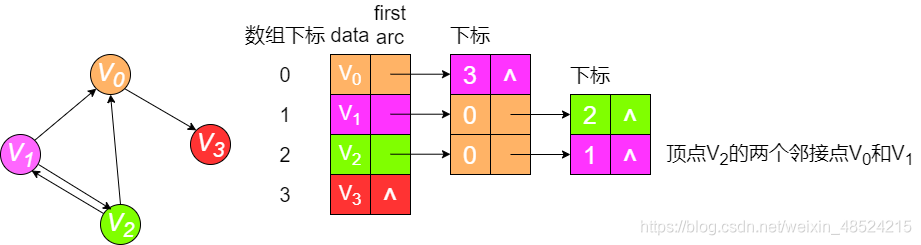

图的邻接表存储表示

#define MVNum 100
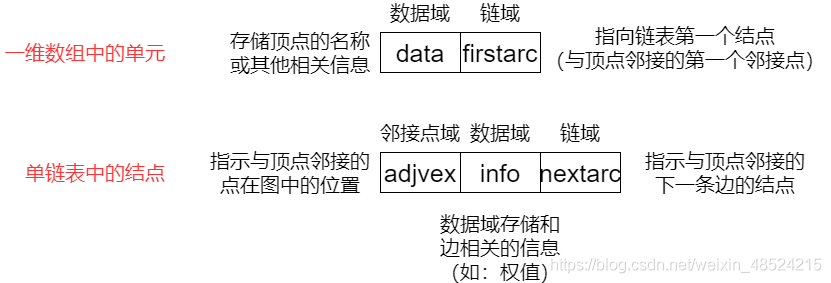
//单链表中的结点
typedef struct ArcNode{	
	int adjvex;	//顶点的第一邻接点在一维数组中的下标
	struct ArcNode *nextarc;	//指向顶点的下一邻接点
	OtherInfo info;	//边信息，如权值
}ArcNode;	
//顶点（存储在一维数组中）
typedef struct VNode{
	VerTexType data;	//顶点信息
	ArcNode *firstarc;	//顶点的第一邻接点
}VNode,AdjList[MVNum];	//AdjList表示邻接表类型
//邻接表
typedef struct{
	AdjList vertices;	//一维数组vertices
	int vexnum,arcnum;	//图的当前顶点数和边数
}ALGraph;

邻接表的广度遍历

void BFSTraverse(ALGraph G){
	p=new ArcNode;	//结点指针
	for(int i=0; i<G.vexnum; ++i)	//初始化标志数组
		visited[i]=false;	//初值设为false，即未被访问过
	InitQueue(Q);	//初始化队列
	for(i=0; i<G.vexnum; ++i){	//遍历邻接矩阵的行
		if(!visited[i]){	//行标为i对应的顶点未被访问，比如i=0,则对应V_0
			visited[i]=true;
			cout << G.vexs[i];	//输出邻接矩阵中行标对应的顶点，比如i=0,则对应V_0
			EnQueue(Q,i);	//行标为i对应的顶点入队
			while(!QueueEmpty(Q)){	//队列非空
				DeQueue(Q,i);	//行标为i对应的顶点出队/队头顶点出队
				p=G.vertices[i].firstarc;	//指针重命名为p
				while(p){	//指针p所指非空
					if(!visited[p->adjvex]){	//!visited[p->adjvex]
						visited[p->adjvex]=true;
						cout << G.vertices[p->adjvex].data;	//输出列标p->adjvex对应的顶点
						EnQueue(Q,p->adjvex); //列标p->adjvex对应的顶点入列
					}
					p=p->nextarc;	//现用p指向p->nextarc所指结点
				}
			}
		}
	}
}