参考文献

• File:Dirichlet.pdf, From Wikipedia, the free encyclopedia
• 画出Dirichlet分布的单纯形图

代码

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.tri as tri
from mpl_toolkits.axes_grid1.inset_locator import inset_axes

# Add font family "Microsoft YaHei" to support Chinese.
# matplotlib.rcParams['font.family'].insert(0, 'Microsoft YaHei')
font_size = 22
matplotlib.rcParams.update({
    'figure.facecolor': 'white',
    'legend.fontsize': font_size,
    'axes.labelsize': font_size,
    'axes.titlesize': font_size,
    'xtick.labelsize': font_size,
    'ytick.labelsize': font_size,
})
# 生成等边三角形
corners = np.array([[0, 0], [1, 0], [0.5, 0.75 ** 0.5]])
triangle = tri.Triangulation(corners[:, 0], corners[:, 1])

# 每条边中点位置
midpoints = [(corners[(i + 1) % 3] + corners[(i + 2) % 3]) / 2.0 for i in range(3)]


# 将三角形顶点的笛卡尔坐标映射到重心坐标系
def xy2bc(xy, tol=1.e-3):
    s = [(corners[i] - midpoints[i]).dot(xy - midpoints[i]) / 0.75 for i in range(3)]
    return np.clip(s, tol, 1.0 - tol)


# 有了重心坐标，可以计算Dirichlet概率密度函数的值
class Dirichlet(object):

    def __init__(self, alpha):
        from math import gamma
        from operator import mul
        from functools import reduce
        self.alpha = np.array(alpha)
        self._coef = gamma(np.sum(self.alpha)) / reduce(mul, [gamma(a) for a in self.alpha])  # reduce:sequence连续使用function

    def pdf(self, x):
        # 返回概率密度函数值
        from operator import mul
        from functools import reduce
        return self._coef * reduce(mul, [xx ** (aa - 1) for (xx, aa) in zip(x, self.alpha)])


def draw_pdf_contours(dist, nlevels=200, subdiv=8, filename=None, **kwargs):
    # 细分等边三角形网格
    refiner = tri.UniformTriRefiner(triangle)
    trimesh = refiner.refine_triangulation(subdiv=subdiv)
    pvals = [dist.pdf(xy2bc(xy)) for xy in zip(trimesh.x, trimesh.y)]

    fig, ax = plt.subplots(dpi=300)
    ax.set_aspect('equal')

    # 画出 color bar
    tcf = ax.tricontourf(trimesh, pvals, nlevels, cmap='Blues', **kwargs)
    axins = inset_axes(ax,
                       width="5%",  # width = 10% of parent_bbox width
                       height="80%",  # height : 50%
                       loc='upper left',
                       bbox_to_anchor=(0.99, 0., 1, 1),
                       bbox_transform=ax.transAxes,
                       borderpad=0,
                       )
    fig.colorbar(tcf, cax=axins)

    # 画三角图（单纯性图）
    ax.tricontour(trimesh, pvals, nlevels, linewidths=0.2, **kwargs)
    ax.set_xlim(0, 1)
    ax.set_ylim(0, 0.75 ** 0.5)
    ax.set_axis_off()
    ax.plot([0, 0.5], [0, 0.75 ** 0.5], c='black', linewidth=0.5)
    ax.plot([0.5, 1], [0.75 ** 0.5, 0], c='black', linewidth=0.5)
    ax.plot([0, 1], [0, 0], c='black', linewidth=1)

    # 给三个顶点添加文本注释
    ax.text(0.32, 0.9, r'$\mathbf{p}=(0, 0, 1)$', fontsize=font_size)
    ax.text(-0.2, -0.07, r'$\mathbf{p}=(1, 0, 0)$', fontsize=font_size)
    ax.text(0.8, -0.07, r'$\mathbf{p}=(0, 1, 0)$', fontsize=font_size)
    ax.set_title(r'$\mathbf{\alpha}=(%s)$' %
                 (", ".join([format(i, ".1f") for i in dist.alpha])),
                 y=-0.25)

    # 保存文件并显示图片
    if filename:
        plt.savefig(filename + '.png', bbox_inches='tight')
        plt.savefig(filename + '.eps', format='eps', bbox_inches='tight')
    plt.show()


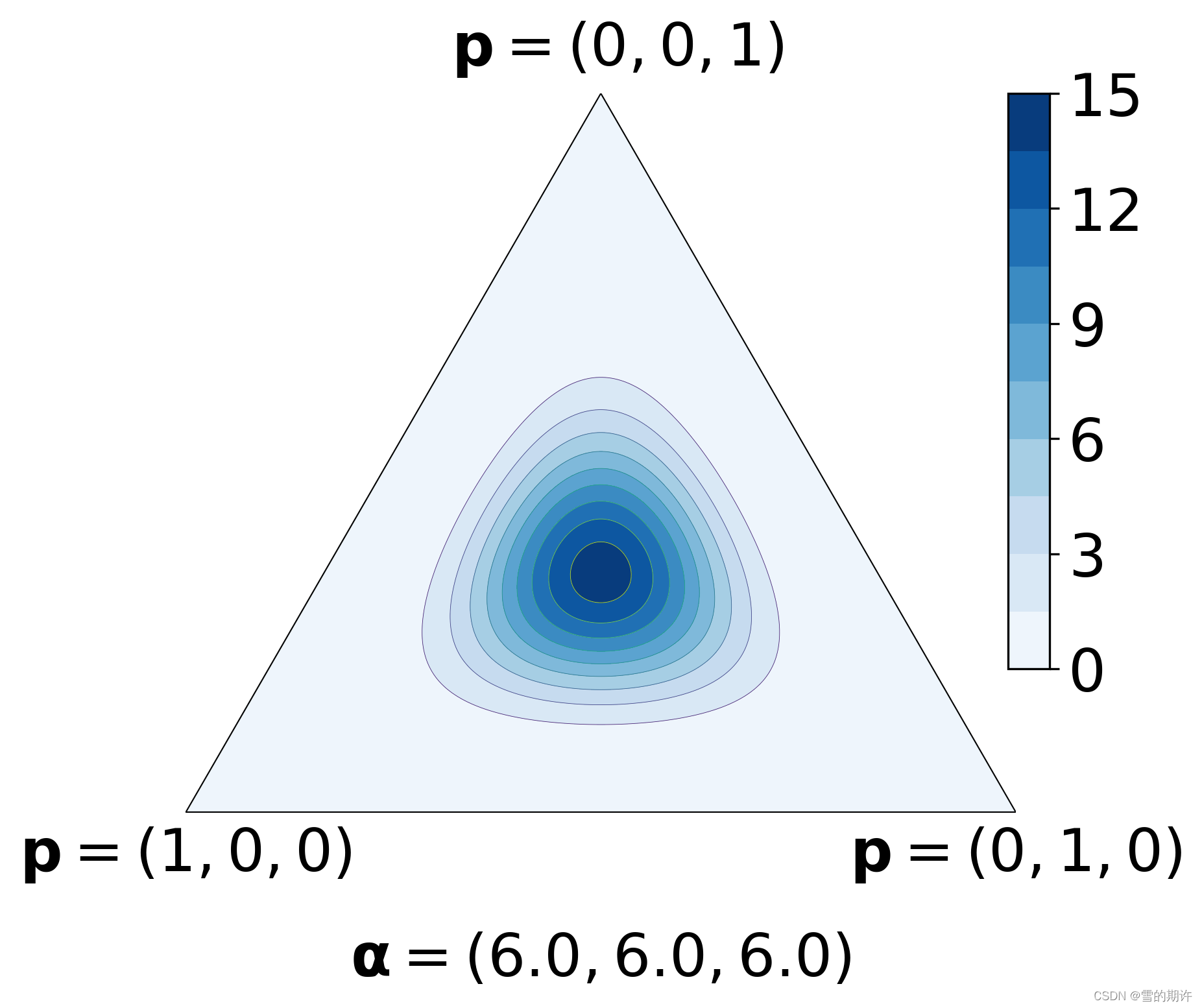
draw_pdf_contours(Dirichlet([6, 6, 6]), nlevels=10, filename='dirichlet-total')
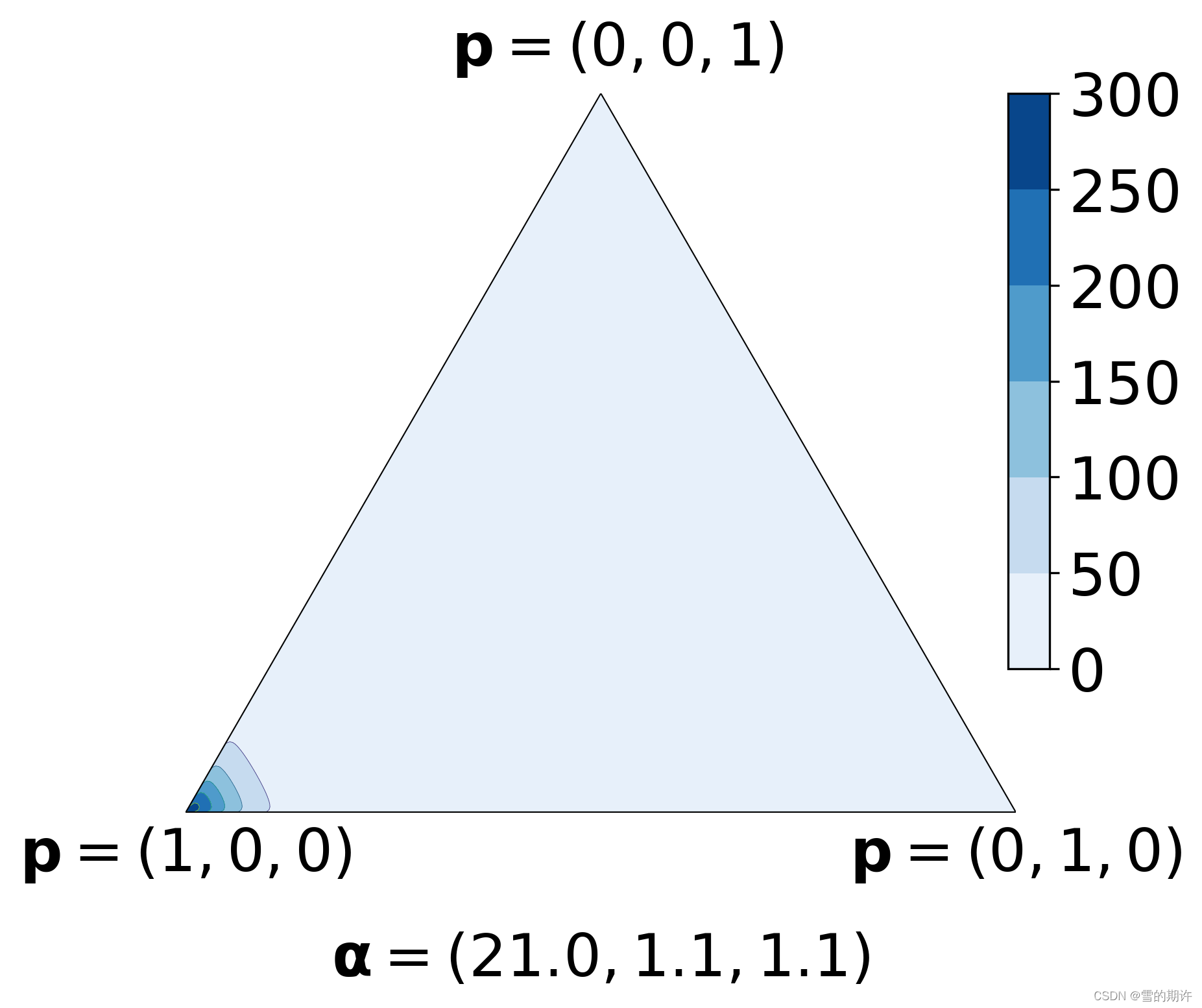
draw_pdf_contours(Dirichlet([21, 1.1, 1.1]), nlevels=5, filename='dirichlet-confident_prediction')
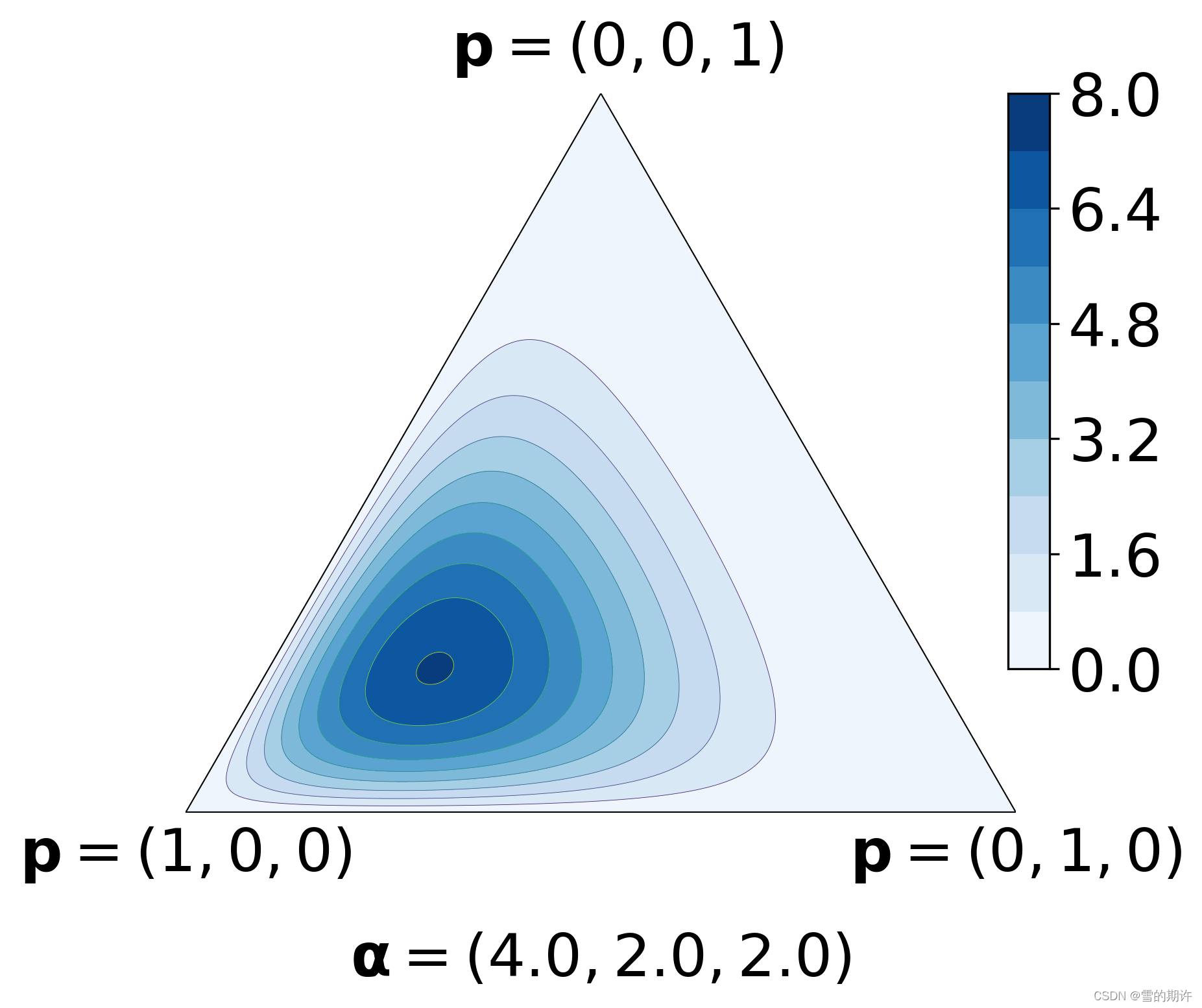
draw_pdf_contours(Dirichlet([4, 2, 2]), nlevels=10, filename='dirichlet-vacuity_prediction')
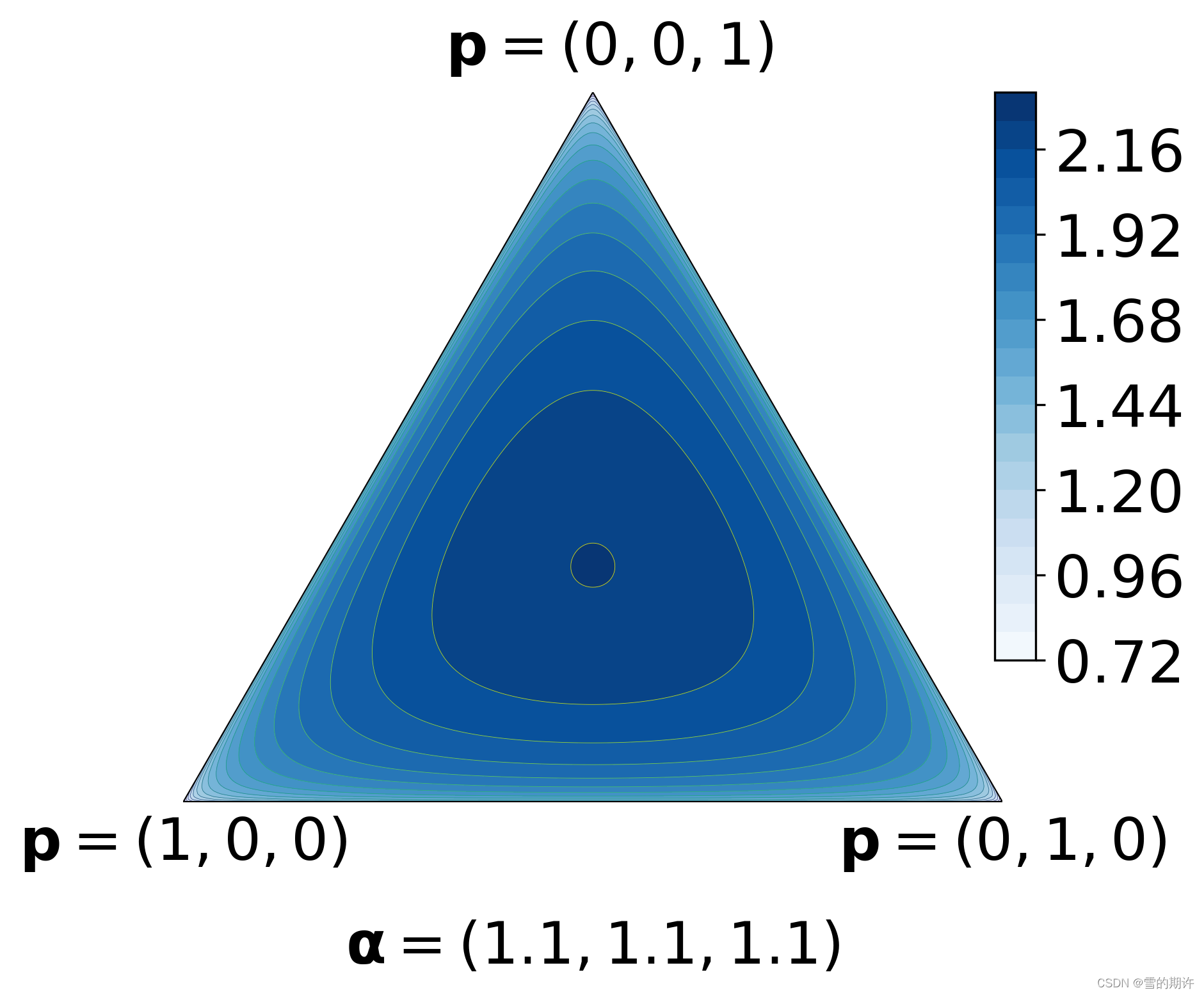
draw_pdf_contours(Dirichlet([1.1, 1.1, 1.1]), nlevels=20, filename='dirichlet-dissonance_prediction')