介绍广度优先搜索算法（BFS），以及BFS算法的应用：迷宫路径问题

将起始节点加入队列，然后不断从队列头部取出节点进行处理（队列的特点：先进先出），并将其未访问的相邻节点加入队列尾部。这样就保证了先访问的节点的相邻节点先被处理，从而实现逐层搜索。它从起始节点开始，依次访问其所有相邻节点，然后再依次访问这些相邻节点的相邻节点，如此逐层向外扩展，就像以起始节点为中心，一层一层地向外扩散搜索。给定一个迷宫，迷宫由 0 和 1 组成，其中 0 表示可以通行，1 表示墙壁。

码力金矿

435人浏览 · 2025-04-17 01:51:41

码力金矿 · 2025-04-17 01:51:41 发布

我前几天已经介绍过深度优先搜索算法（DFS）,见以下链接：
https://blog.csdn.net/lbh73/article/details/147235900?spm=1011.2415.3001.5331

现在介绍另一种：广度优先搜索算法（BFS）。
在大厂笔试中，这俩种关于图的搜索算法几乎是必考题，也是数据结构课程中的重要内容。

（文章末尾可扫码加V）

广度优先搜索是一种基于队列数据结构的搜索算法。它从起始节点开始，依次访问其所有相邻节点，然后再依次访问这些相邻节点的相邻节点，如此逐层向外扩展，就像以起始节点为中心，一层一层地向外扩散搜索。

使用队列来实现广度优先搜索。将起始节点加入队列，然后不断从队列头部取出节点进行处理（队列的特点：先进先出），并将其未访问的相邻节点加入队列尾部。这样就保证了先访问的节点的相邻节点先被处理，从而实现逐层搜索。

以下是关于BFS算法的应用。

迷宫路径问题
题目描述
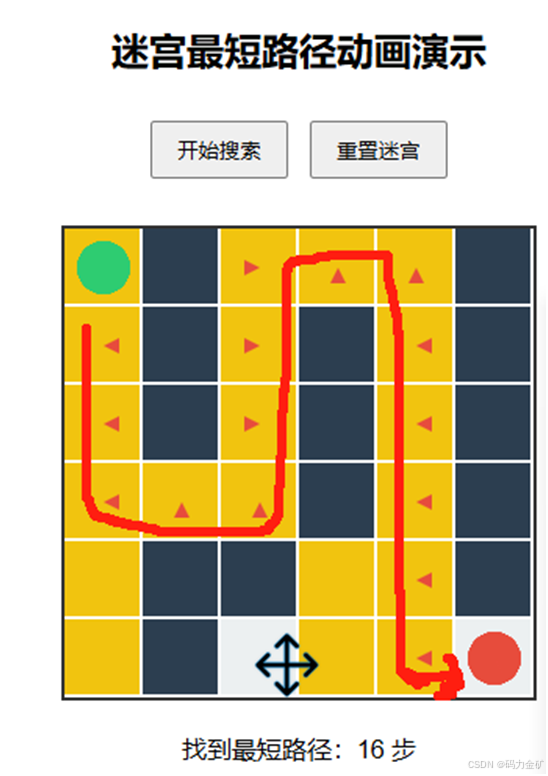
给定一个迷宫，迷宫由 0 和 1 组成，其中 0 表示可以通行，1 表示墙壁。从起点 (0, 0) 到终点 (n-1, n-1) 的最短路径长度是多少？

问题分析：这是一个典型的最短路径问题，可以使用广度优先搜索（BFS）来解决。
解题步骤：
• 使用队列存储当前访问的节点。
• 每次从队列中取出一个节点，探索其四个方向（上、下、左、右）。
• 如果到达终点，返回当前步数。

from collections import deque
'''作用：导入双端队列（deque），用于实现高效的队列操作。
deque的popleft()操作时间复杂度为O(1)，远优于列表的O(n)，适合BFS的先进先出特性。
'''

DIRECTIONS = [(-1, 0), (1, 0), (0, -1), (0, 1)]  # 上下左右移动

START = (0, 0)
#END = (4, 4) 
END = (5, 5)#如果维度有变化，需要修改此地方，例如如果思维为4，那么就修改为：END = (4, 4)

# 可配置参数区（迷宫参数如有变动，用户需修改此区域）
'''
MAZE = [
    [0, 1, 0, 0, 0],
    [0, 1, 0, 1, 0],
    [0, 1, 0, 1, 0],
    [0, 0, 0, 1, 0],
    [0, 1, 1, 0, 0]
]
'''

MAZE = [
    [0, 1, 0, 0, 0, 1],
    [0, 1, 0, 1, 0, 1],
    [0, 1, 0, 1, 0, 1],
    [0, 0, 0, 1, 0, 1],
    [0, 1, 1, 0, 0, 1],
    [0, 1, 0, 0, 0, 0]
]

'''
作用：定义迷宫（0为通路，1为障碍）、起点、终点和移动方向（上下左右）。
DIRECTIONS表示四个可能的移动方向，与BFS中探索相邻节点的逻辑一致。
'''

def validate_maze(maze, start, end): # 检查坐标越界和起点/终点是否可达
    """验证迷宫合法性"""
    if not maze or not maze[0]:
        raise ValueError("迷宫不能为空")
    if start[0] < 0 or start[1] < 0 or end[0] >= len(maze) or end[1] >= len(maze[0]):
        raise ValueError("坐标越界")
    if maze[start[0]][start[1]] != 0 or maze[end[0]][end[1]] != 0:
        raise ValueError("起点/终点不可达")
'''
作用：验证迷宫的合法性：
迷宫非空且至少有一行。
起点和终点的坐标不越界。
起点和终点必须为通路（值为0）。
边界条件检查逻辑
'''


def bfs_shortest_path(maze, start, end):
    """
    使用BFS算法计算最短路径
    :param maze: 二维迷宫数组
    :param start: 起始坐标元组
    :param end: 终点坐标元组
    :return: 最短路径长度（不可达返回-1）
    """
    validate_maze(maze, start, end) # 合法性检查

    rows, cols = len(maze), len(maze[0])
    visited = [[False] * cols for _ in range(rows)] # 访问标记矩阵
    queue = deque([(start[0], start[1], 0)]) # 初始化队列（坐标+步数）
    visited[start[0]][start[1]] = True
    """	
    作用：
    validate_maze确保输入合法。
    visited矩阵记录节点是否已访问，避免重复探索。
    队列初始化为起点坐标和初始步数0，符合BFS的层级扩展特性。
    """


    while queue:
        x, y, steps = queue.popleft()# 取出队首节点

        if (x, y) == end:
            return steps # 找到终点，返回步数

        for dx, dy in DIRECTIONS: # 遍历四个方向
            nx, ny = x + dx, y + dy
            if 0 <= nx < rows and 0 <= ny < cols: # 检查边界
                if not visited[nx][ny] and maze[nx][ny] == 0:
                    visited[nx][ny] = True
                    queue.append((nx, ny, steps + 1)) # 新节点入队

    return -1 # 队列为空未找到路径

'''
作用：
逐层探索：按层级取出节点，确保首次到达终点的路径是最短的（BFS特性）。
方向遍历：对上下左右四个方向生成新坐标，过滤越界位置。
通路检查：仅当相邻节点未被访问且为通路时，将其加入队列并标记为已访问。
步数记录：每次扩展新节点时步数+1，最终返回的步数即为最短路径长度。
'''


if __name__ == "__main__":  # 根据结果输出路径长度或不可达提示
    try:
        result = bfs_shortest_path(MAZE, START, END)
        if result != -1:
            print(f"最短路径长度是{result}")
        else:
            print("没有可达路径")
    except ValueError as e:
        print(f"输入错误：{str(e)}")
'''
作用：
执行BFS算法并捕获可能的输入错误（如非法迷宫配置）。
结果处理：若有解则输出步数，否则提示无可达路径。
'''

'''
关键设计点
队列选择：使用deque而非列表，提升 popleft() 效率。
步数跟踪：队列元素包含步数信息(参考变量steps)，避免额外存储路径节点。
层级扩展：通过步数递增实现逐层探索，确保最短路径优先找到。
合法性检查：在算法开始前验证输入，提高鲁棒性。
'''