目录

一、旅行商问题

二、TSP问题的禁忌搜索算法python实现

2.1 python代码

2.2  禁忌表长度为10的运行结果

2.3 禁忌表长度为50的运行结果

三、禁忌表长度对算法性能的影响

四、禁忌长度的设置方法

---

一、旅行商问题

以旅行商问题（TSP）为例，编写以下程序实现禁忌搜索算法。分别设置禁忌表长度为10、50，最大迭代步数统一为1000。

city30的数据如下：

city_x=[41, 37, 54, 25, 7, 2, 68, 71, 54, 83, 64, 18, 22, 83, 91, 25, 24, 58, 71, 74, 87,18, 13, 82, 62, 58, 45,41,44, 4]
city_y=[94, 84, 67, 62, 64, 99, 58, 44, 62, 69, 60, 54, 60, 46, 38, 38, 42, 69, 71, 78, 76,40, 40, 7, 32, 35, 21,26,35, 50]

二、TSP问题的禁忌搜索算法python实现

2.1 python代码

import random
from itertools import combinations
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False


'''计算路径总路程的函数'''
def fitness(n,X,Y,X0):
    '''n——城市的数量；
       X——n个城市的横坐标；
       Y——n个城市的纵坐标；
       X0——一个解向量'''
    s=0
    for i in range(n):
        if i!=n-1:
            s=s+np.sqrt((X[X0[i]]-X[X0[i+1]])**2+(Y[X0[i]]-Y[X0[i+1]])**2)
        else:
            s=s+np.sqrt((X[X0[i]]-X[X0[0]])**2+(Y[X0[i]]-Y[X0[0]])**2)
    return s


'''定义领域搜索运算操作——交换操作'''
def exchange(X0,q):
    '''X0——一个解向量；
       q——指定的需要进行交换操作的领域列表，长度为2'''
    temp=X0[q[0]]
    X0[q[0]]=X0[q[1]]
    X0[q[1]]=temp
    return X0


'''得到所有领域组合的函数'''
def combiantion(n):
    '''n——城市数量'''
    q=[]
    b=[int(i) for i in range(n)]
    for i in combinations(b,2):
        q.append(list(i))
    return q


'''定义添加和删除禁忌表中元素的函数'''
def Tabu_add_remove(Tabu_len,T,q):
    '''
    :param Tabu_len: 禁忌表的长度
    :param T: 禁忌表
    :param q: 需要添加到禁忌表中的元素
    :return: 经过处理后的禁忌表
    '''
    if len(T)<Tabu_len:
        T.append(q)
    else:
        T=[*T[1:],q]
    return T


'''禁忌搜索算法——TSP'''
def TS_TSP(X0,Tabu_len,T,NG,n,X,Y):

    '''
    :param X0: 初始解
    :param Tabu_len:禁忌表的长度
    :param T: 禁忌表
    :param NG: 最大迭代步数
    :param n: 城市数量
    :param X: n个城市的横坐标
    :param Y: n个城市的纵坐标
    :return: 最优路径和每一次迭代得到的解的函数值和每一次迭代得到的历史最优解的函数值
    '''

    '''得到所有可能的领域组合'''
    q=combiantion(n)

    '''初始化目标函数值'''
    c=fitness(n,X,Y,X0)

    '''初始化历史最优值'''
    c_min=c

    '''初始化历史最优值所对应的路径'''
    X_min=X0

    '''存储每一次迭代产生的解的函数值'''
    M=[]
    M.append(c)

    '''存储每一次迭代的历史最优解的函数值'''
    N=[]
    N.append(c_min)

    '''存储每一次迭代的最优路径'''
    Xmin=[]
    Xmin.append(X_min)


    '''进行禁忌搜索算法'''
    for i in range(NG):
        #存储适配值的列表
        Q=[]
        for j in range(len(q)):
            #复制初始解
            P=X0.copy()
            #交换操作
            P=exchange(P,q[j])
            #计算交换后的解的总路程
            s2=fitness(n,X,Y,P)
            Q.append(s2)

        #得到对适配值列表Q升序排列后的索引
        index_sort=np.argsort(np.array(Q))
        #对Q进行升序排列
        Q_sort=[Q[k] for k in index_sort]
        #得到Q降序排列相对应的变换领域
        q_sort=[q[k] for k in index_sort]

        '''更新禁忌表'''
        for j in range(len(q_sort)):
            if q_sort[j] not in T:
                T=Tabu_add_remove(Tabu_len,T,q_sort[j])
                #目标函数值
                c=Q_sort[j]
                #更新解
                X0=exchange(X0,q_sort[j])
                #更新历史最优值和历史最优路径
                if Q_sort[j]<c_min:
                    c_min=Q_sort[j]
                    X_min=X0.copy()
                    Xmin.append(X_min)
                M.append(c)
                N.append(c_min)
                break
            if q_sort[j] in T:
                if Q_sort[j]<c_min:    #满足渴望水平
                    #目标函数值
                    c=Q_sort[j]
                    #更新禁忌表
                    T=Tabu_add_remove(Tabu_len,T,q_sort[j])
                    #更新解
                    X0=exchange(X0,q_sort[j])
                    c_min=Q_sort[j]
                    X_min=X0.copy()
                    M.append(c)
                    N.append(c_min)
                    Xmin.append(X_min)
                    break

    '''绘制禁忌搜索算法下的优化过程'''
    plt.plot([int(i) for i in range(NG+1)],N,c="orange")
    plt.title("禁忌搜索算法——TSP的优化过程")
    plt.xlabel("代数")
    plt.ylabel("总路程")
    plt.grid()
    plt.show()

    '''绘制路径图'''
    #最优路径
    X1=Xmin[-1]
    #x轴坐标
    x=[city_x[i] for i in X1]
    #y轴坐标
    y=[city_y[i] for i in X1]
    #绘制散点图
    plt.scatter(x,y,marker="o",c="red")
    #绘制折线图
    for i in range(n):
        if i!=n-1:
            plt.plot([x[i],x[i+1]],[y[i],y[i+1]],c='plum')
        else:
            plt.plot([x[i],x[0]],[y[i],y[0]],c='plum')
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("路径图")
    plt.show()

    return Xmin,M,N


'''主函数'''
if __name__=="__main__":

    '''城市的数量'''
    n=30

    '''定义30个城市的坐标'''
    city_x=[41, 37, 54, 25, 7, 2, 68, 71, 54, 83, 64, 18, 22, 83, 91, 25, 24, 58, 71, 74, 87,
            18, 13, 82, 62, 58, 45,41,44, 4]
    city_y=[94, 84, 67, 62, 64, 99, 58, 44, 62, 69, 60, 54, 60, 46, 38, 38, 42, 69, 71, 78, 76,
            40, 40, 7, 32, 35, 21,26,35, 50]

    '''随机得到初始解'''
    X0=random.sample(range(n),n)
    print("初始解X0：\n{}".format(X0))

    '''定义最大迭代步数'''
    NG=1000

    '''定义禁忌表的长度'''
    Tabu_len=50

    '''定义禁忌表'''
    T=[]

    '''禁忌搜索算法'''
    Xmin,M,N=TS_TSP(X0,Tabu_len,T,NG,n,city_x,city_y)

    print("最优路径：")
    for i in range(len(Xmin[-1])):
        if i!=len(Xmin[-1])-1:
            print("{}—>".format(Xmin[-1][i]),end="")
        else:
            print("{}—>{}".format(Xmin[-1][i],Xmin[-1][0]))
    print("最短路程：\n{}".format(N[-1]))
    #print("每一次迭代得到的解的函数值：\n{}\n".format(M))
    #print("每一次迭代得到的历史最优解的函数值：\n{}\n".format(N))

2.2  禁忌表长度为10的运行结果

 

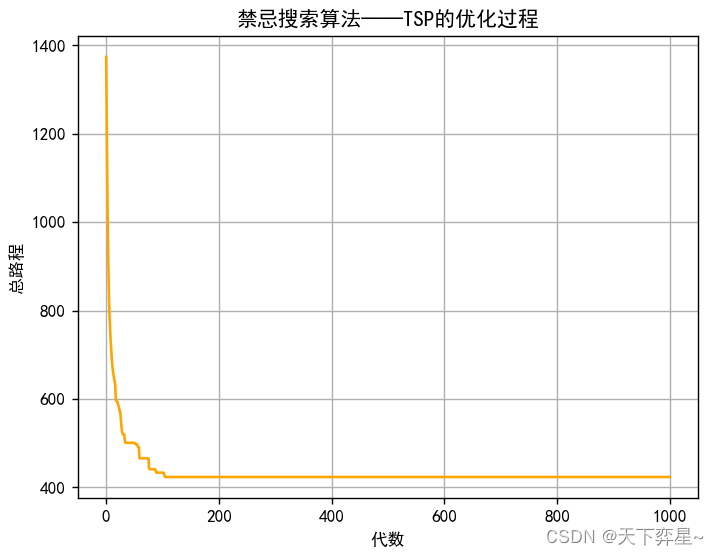
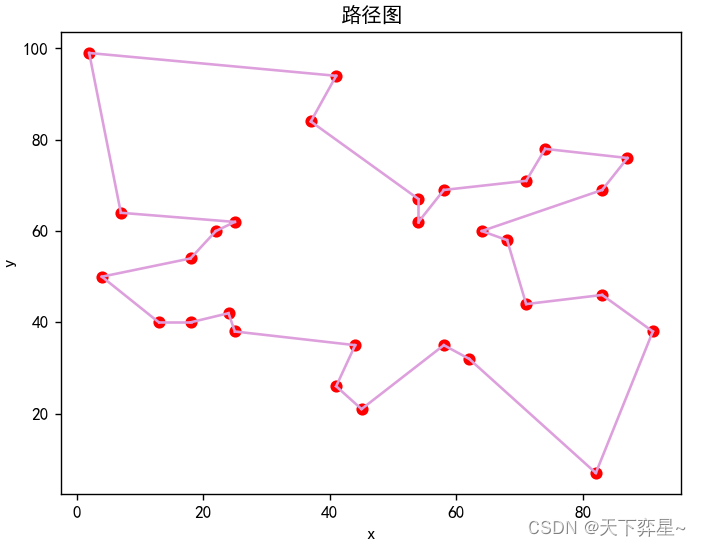
2.3 禁忌表长度为50的运行结果

 

  

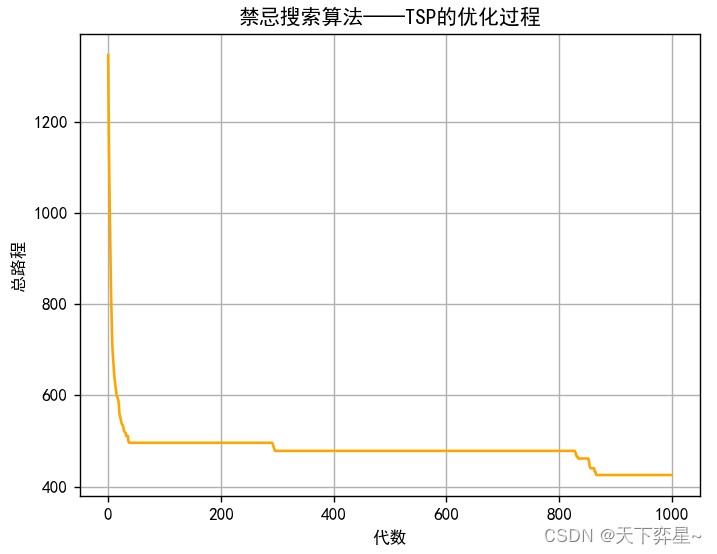
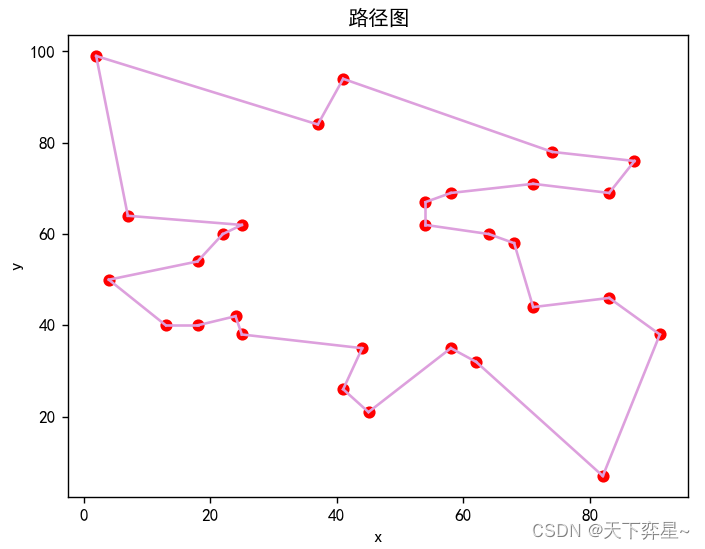
三、禁忌表长度对算法性能的影响

（1）禁忌表的长度越小，计算时间和存储空间越少。如果禁忌长度过小，会造成搜索的循环。

（2）如果禁忌表比较长，便于在更广阔的区域搜索，光宇搜索性能比较好；而禁忌表比较短，则是的搜索在小的范围进行，局部搜索性能比较好。

总而言之，就禁忌长度的选择而言，禁忌长度越短，机器内存占用越少，解禁范围更大（搜索范围上限越大），但很容易造成搜索循环（实际去搜索的范围却很小），过早陷入局部最优。禁忌长度过长又会导致计算时间过长。

四、禁忌长度的设置方法

1. 禁忌长度t固定不变。t可以取一些与问题无关的常数，例如t=5,7,11等值。
2. 禁忌长度t与问题的规模相关，例如取，这里n为问题的规模。
3. 禁忌长度t随迭代的进行而改变。根据迭代的具体情况，按照某种规则，禁忌长度在区间内变化。这个禁忌长度的区间可以与问题无关，例如[1,10]；或者与要求解问题的规模有关，例如。而这个区间的两个端点也可以随着迭代的进行而改变。