目录

搜索算法介绍

DFS:

基本步骤：

BFS：

基本步骤：

动图算法

棋盘跳马问题

问题描述

算法思路： 

算法实现：

搜索算法介绍

DFS:

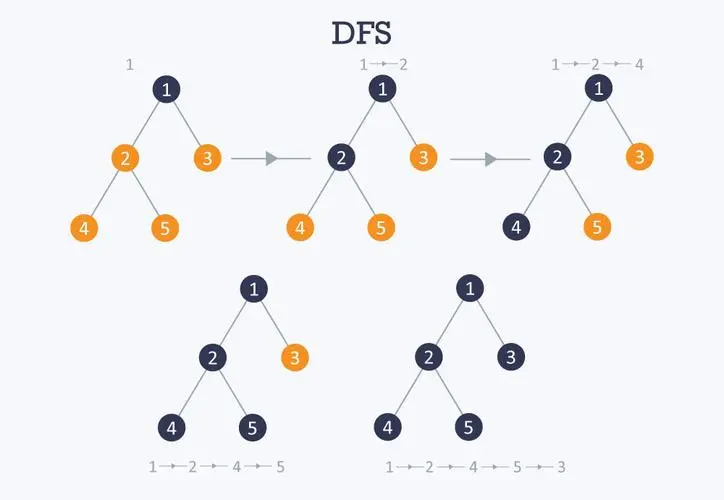
深度优先搜索（Depth-First Search，简称DFS）是一种用于遍历或搜索树或图的算法。这种算法会尽可能深地搜索图的分支，直到找到目标节点或达到叶节点（没有子节点的节点），然后回溯到上一个分支继续搜索。DFS可以用于许多问题，比如路径寻找、连通性验证、拓扑排序等。

在ACM、蓝桥杯等著名竞赛中DFS算法是比较重要的，特别是在蓝桥杯中每一年几乎都要考DFS/BFS算法。DFS算法在OI赛中用处非常大，可以通过DFS/BFS暴力的方式可以拿到部分分数，蓝桥杯一般可以拿到20%的分数，有的甚至高达50%，是暴力得分的不二之选。

基本步骤：

DFS通常使用递归或栈来实现。以下是DFS的基本步骤：

选择起始点：选择图中的一个点作为起始点。
访问节点：标记起始节点为已访问，并将该节点加入递归或栈中。
探索邻接节点：从该点周围取出一个点，检查它的所有未访问的邻接节点。
递归或迭代：对每个未访问的邻接节点，将其标记为已访问，然后将其推入递归或栈中。
回溯：当当前节点的所有邻接节点都被访问后，递归中回溯/从栈中弹出该节点，继续搜索上一个点的其他分支。
结束条件：当栈为空或找到目标节点时，搜索结束。

---

BFS：

广度优先搜索（Breadth-First Search，简称BFS）是一种遍历或搜索树和图的算法，也称为宽度优先搜索，BFS算法从图的某个节点开始，依次对其所有相邻节点进行探索和遍历，然后再对这些相邻节点的相邻节点进行探索，直到遍历完所有的节点。BFS算法使用队列来辅助实现，将起始节点放入队列中，然后依次取出队列中的节点，访问其相邻节点，并将其加入队列。这样可以保证从起始节点出发，依次按照距离顺序遍历节点。BFS常用于寻找最短路径，因为它按照从起点到每个节点的距离来探索节点。

在ACM、蓝桥杯等著名竞赛中BFS算法是比较重要的，特别是在蓝桥杯中每一年几乎都要考DFS/BFS算法。BFS算法在OI赛中用处非常大，可以通过DFS/BFS暴力的方式可以拿到部分分数，蓝桥杯一般可以拿到20%的分数，有的甚至高达50%，是暴力得分的不二之选。

基本步骤：

BFS算法通常使用队列来实现，BFS算法的具体步骤如下：

创建一个队列，将起始节点加入队列；
创建一个集合，用于存储已经访问过的节点；
从队列中取出一个节点，并将其标记为已访问；
访问该节点的所有相邻节点，如果相邻节点未被访问，则将其加入队列；
重复步骤3和步骤4，直到队列为空。
BFS算法可以用来解决一些问题，例如图的遍历、最短路径搜索等。由于BFS算法保证了按照距离顺序遍历节点，因此可以用来寻找最短路径。另外，BFS算法还可以用来判断图是否连通，即从一个节点是否可以到达另一个节点。

---

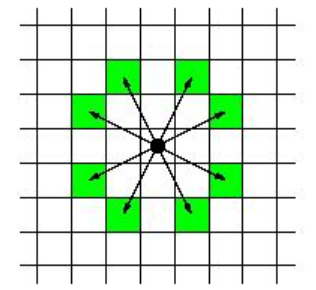
动图算法

红色遍历为BFS宽度优先搜索，黄色为DFS深度优先搜索，绿色为起点，紫色为终点，黑色为障碍物）。 

---

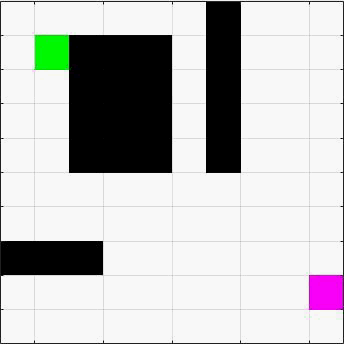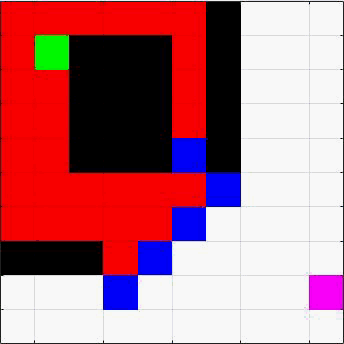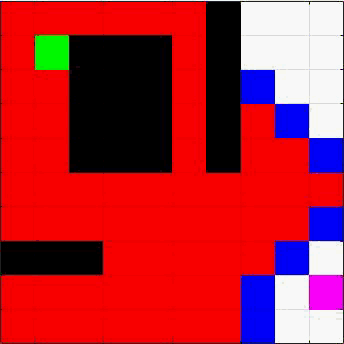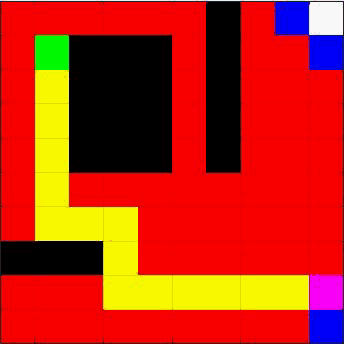
棋盘跳马问题

问题描述

　　一个8×8的棋盘上有一个马初始位置为(a,b)，他想跳到(c,d)，问是否可以？如果可以，最少要跳几步？

输入格式

　　一行四个数字a,b,c,d。

输出格式

　　如果跳不到，输出-1；否则输出最少跳到的步数。

样例输入

1 1 2 3

样例输出

1

数据规模和约定

　　0<a,b,c,d≤8且都是整数。

算法思路： 

这道题是经典的跳马搜素问题，可以选择BFS、DFS，BFS用时会小一点，毕竟DFS会回溯。但是还是dfs好理解，dfs做此类题目还是最经典的，我们可以按照dfs上面所说的步骤进行写算法，思路还是很清晰的，具体的详解写在了代码上了。

算法实现：

#include<iostream>
using namespace std;
int a,b,c,d;
int vis[10][10];//标记数组
int sum=64;//能到达的方法数，最大为8*8的格子全部走一遍，初始值为8*8，因为要找最小值
int dx[]={1,1,-1,-1,2,2,-2,-2};//方向数组X
int dy[]={2,-2,2,-2,1,-1,1,-1};//方向数组Y
void dfs(int x,int y,int dep){//dfs搜索
	if(dep>=sum){//如果当前步数大于最小步数则没有意义继续搜下去了，直接return
		return;
	}
	if(x==c&&y==d){//到达终点坐标(c,d)
		if(dep<sum){//判断步数是否小于最小步数，小于就更新
			sum=dep;
		}
		return;
	}
	for(int i=0;i<8;i++){//8个方向搜索
		int bx=x+dx[i];
		int by=y+dy[i];
		if(vis[bx][by]==1){//已经走过就不走了
			continue;
		}
		if(bx<=0||bx>8||by<=0||by>8){//不在边界范围内也不走
			continue;
		}//判断完说明该点可以走
		vis[bx][by]=1;//走就标记为走过
		dfs(bx,by,dep+1);//继续dfs
		vis[bx][by]=0;//回溯，解标记
	}
}
int main(){
	cin>>a>>b>>c>>d;
	vis[a][b]=1;//先把起点标记为走过，不然对后面搜索有影响
	dfs(a,b,0);//起点开始搜索
	if(sum==64){//如果sum还等于64，就说明sum就没有被更新过，也就是说根本到达不了终点
		cout<<-1;
	}else{
		cout<<sum;
	}
	return 0;
}

最后，博主也去提交验证了一下，AC了，耗时也比较少。

 本人小白一枚，能力有限，希望各位大佬理解。本文有错误的地方请指出，共同进步。执笔至此，感触彼多，全文将至，落笔为终，感谢大家的支持。