为什么要把 "导数与微分" 作为第二章的标题？

这是因为 导数与微分 之间紧密的关系：

1) 导数是微分的“来源”：导数 f′(x) 表示的是函数 f(x) 在某一点的瞬时变化率，而微分是通过这个变化率来近似描述函数值的变化。微分可以看作是导数的实际应用，表达的是函数值如何随着自变量的微小变化而变化。

2) 微分的几何意义：在几何上，微分 dy 就是切线上的一个小段，而导数 f′(x) 则是这条切线的斜率。两者密切相关，因为切线的斜率决定了微分的大小。

一、引例

1. 直线运动的速度

通过直线运动的速度问题引入导数的基本概念，讨论了瞬时速度的数学定义及其计算方法。通过物理情景直观解释导数的基本思想，为后续微积分的学习奠定基础。下面进行简要总结：

2. 切线问题

通过切线问题进一步解释导数的几何意义，描述了曲线在某点处切线的定义及其计算方法。将切线问题与导数联系起来，为导数的几何解释提供了清晰的图像支持。以下是简要总结：

二、导数的定义

1. 函数在一点处的导数与导函数 

1）定义

2）导数定义式的其他形式

3）函数变化率与导数之间的关系

1.变化率问题的普遍性：
实际中，各种“变化快慢”的问题都可以归结为数学上的函数变化率问题。
导数的概念是对函数变化率的精确数学描述。 

2.导数的意义：
导数不仅是数学概念，也有物理或几何等方面的特殊含义。
从纯粹的数量关系角度，变化率反映了因变量（如 y）相对于自变量（如 x）的变化速度。

3.平均变化率与瞬时变化率：

4.核心观点：
导数是自变量变化引起的因变量变化快慢的极限描述。
它连接了数学公式与实际问题（如速度、增长率等），是变化率问题的核心工具。

4）不可导与导数为无穷大

5）导函数

导数是指函数在某一点x0可导，而导函数是指函数在开区间内每个点都可导。

三个注意点(特别注意第③点)：

2. 导函数举例

1）例题

下面的例题讲述了常见求导导数及其推导。

3. 单侧导数

1）左导数与右导数的定义

2）函数在x0可导的充分必要条件

3）左导数与右导数统称为单侧导数

4）闭区间可导

导数表如下：

三、导数的几何意义

1）导数的几何意义

2）切线方程

3）法线方程

4）切线法线示意图

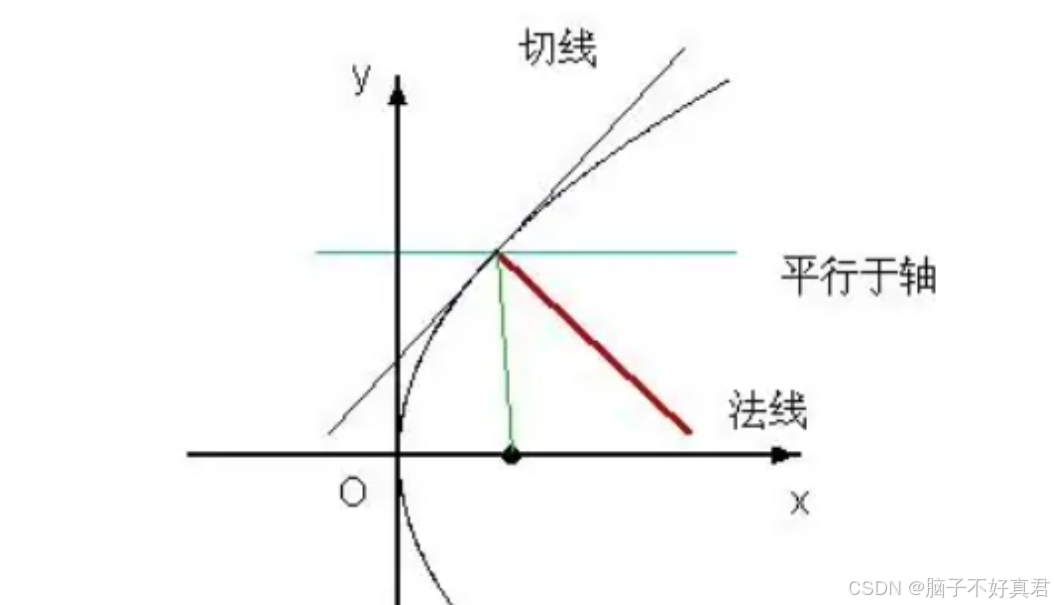
5）例题

下面的例8、例9讲解了已知曲线方程和点坐标，求解该点处的切线方程与法线方程的过程和方法。

四、函数可导性与连续性的关系

1）可导一定连续，连续不一定可导

让我想起了一张图：

2）例题

下面的例10、例11举例说明了连续不一定可导。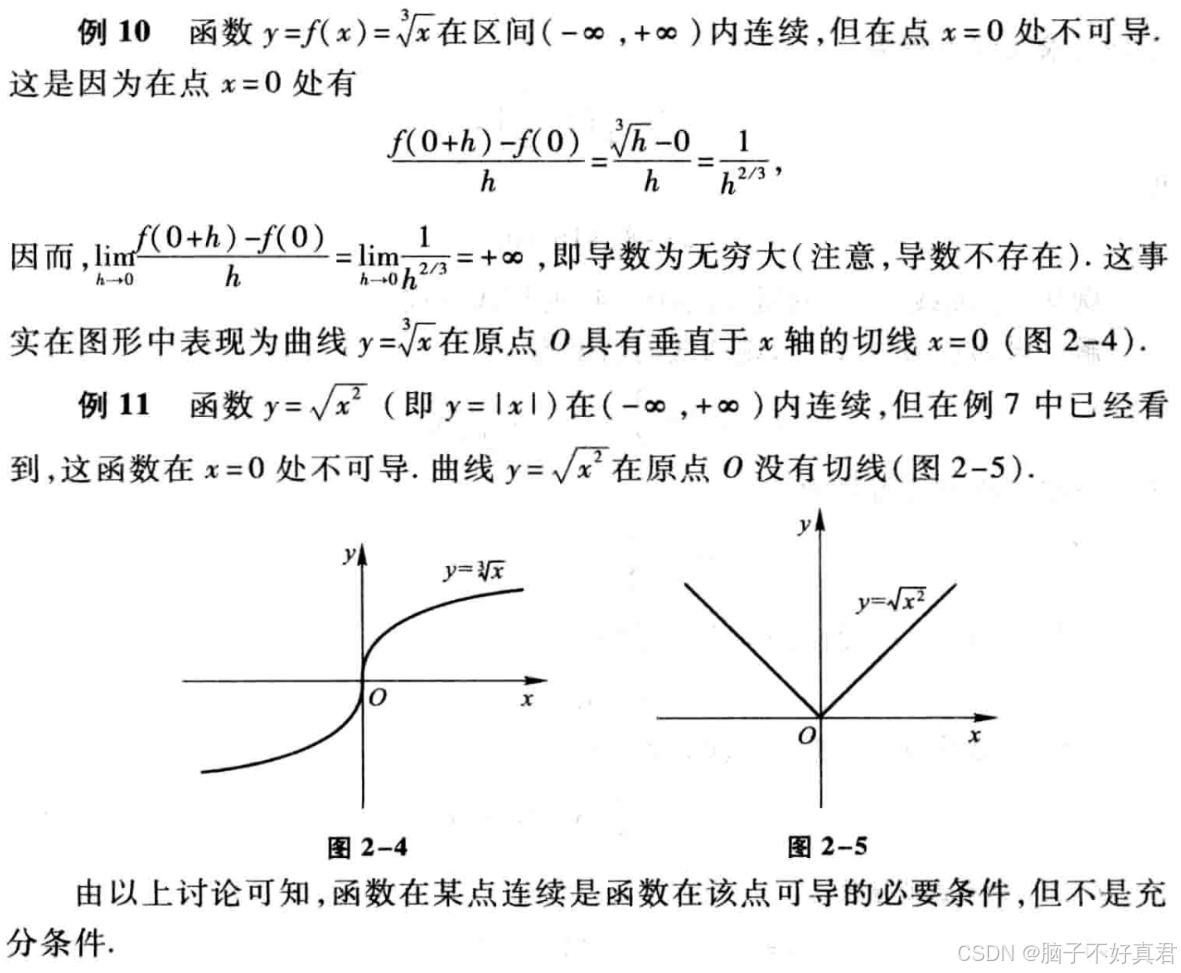

习题 2-1

1.

2.

3.

4.

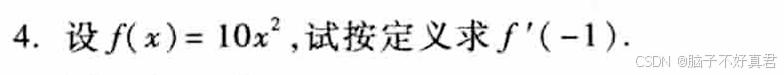
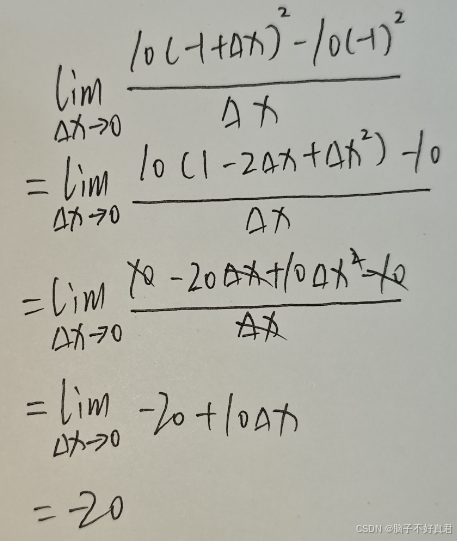
5.

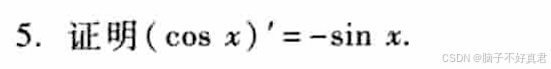
6.

7.

8.

9.

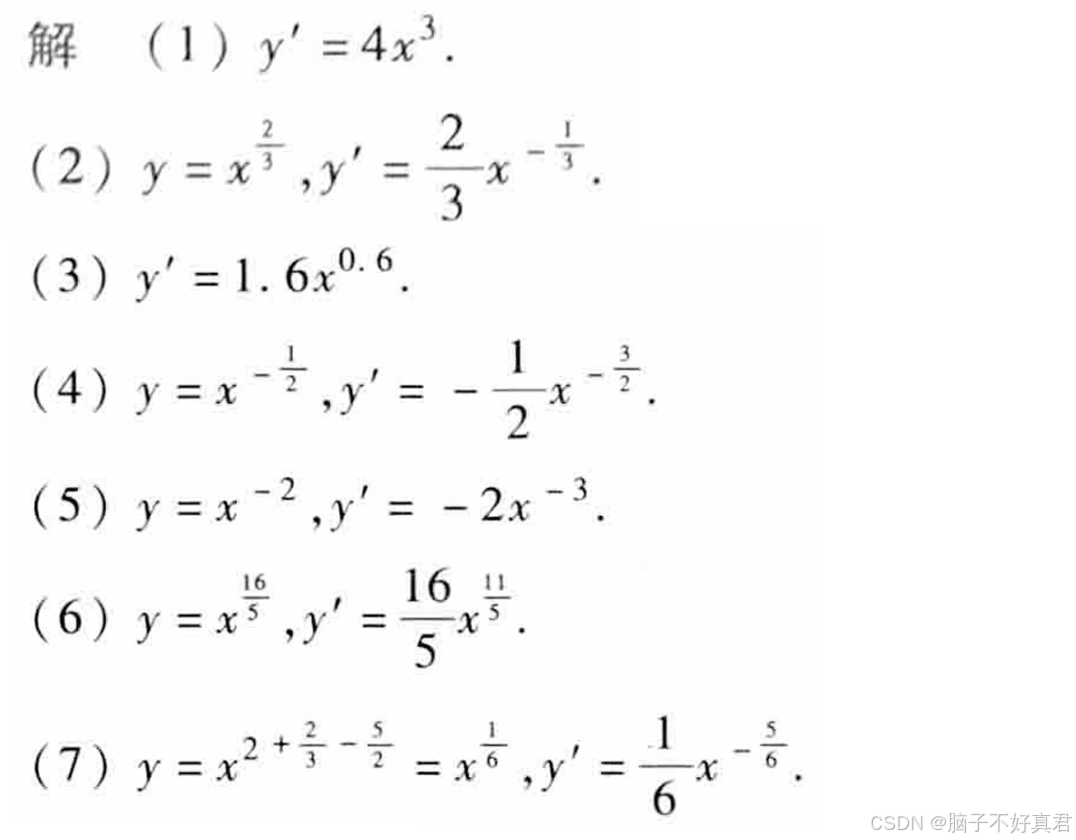
10.

11.

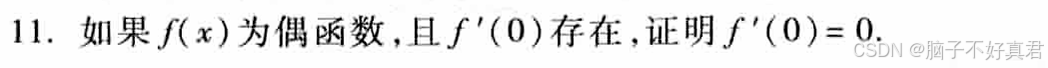
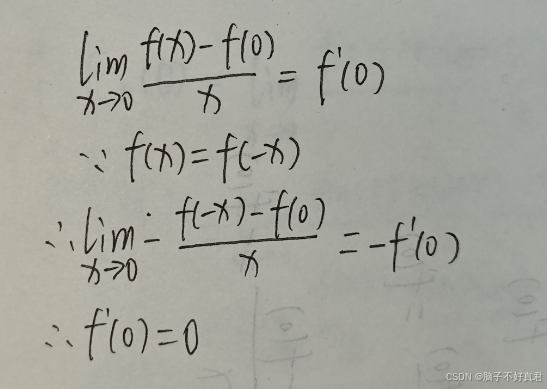
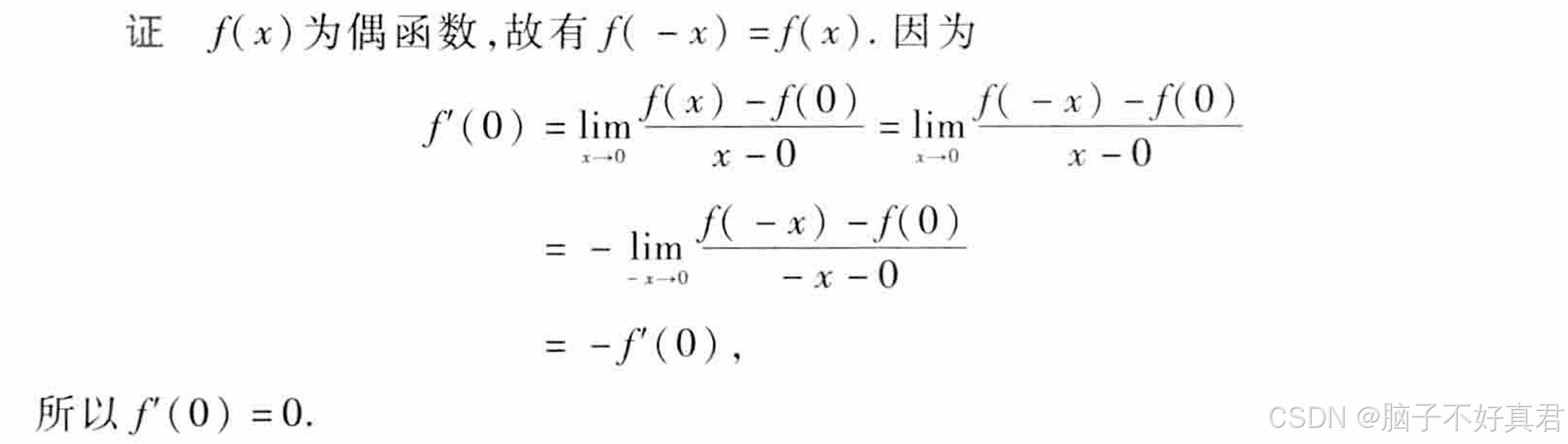
12.

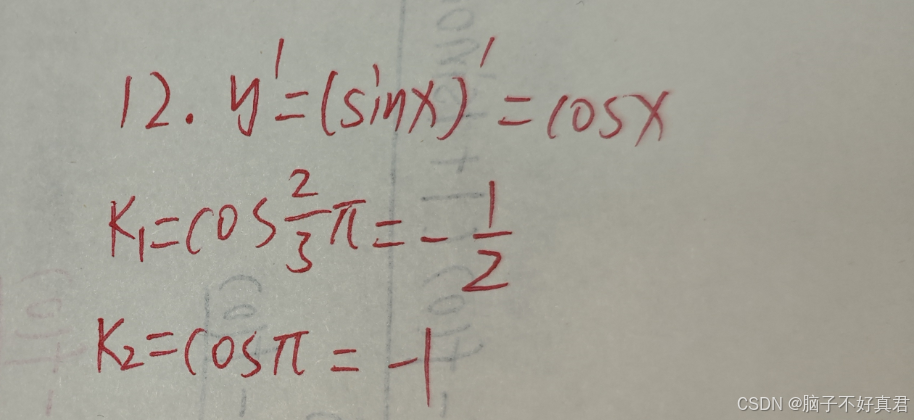
13.

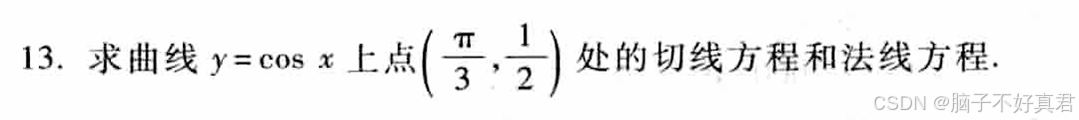
14.

15.

16.

17.

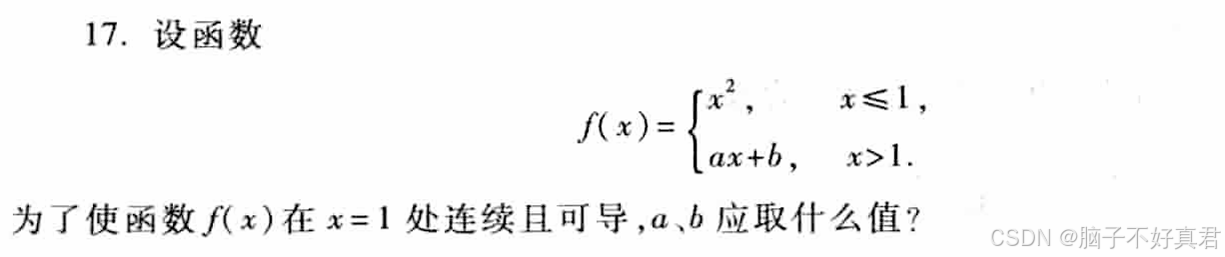
18.

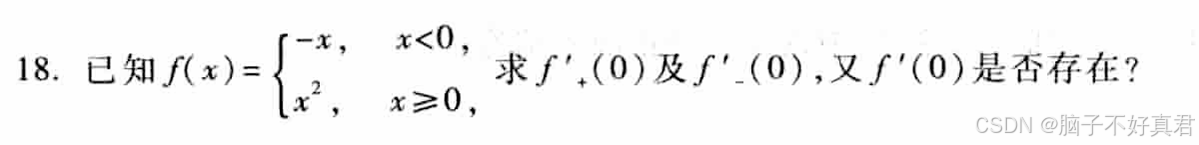
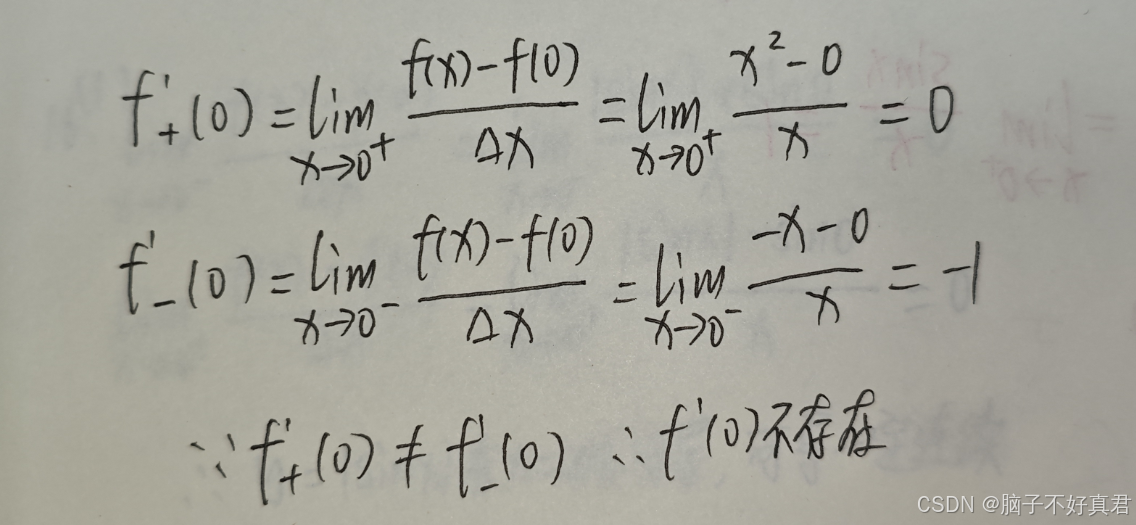
19.

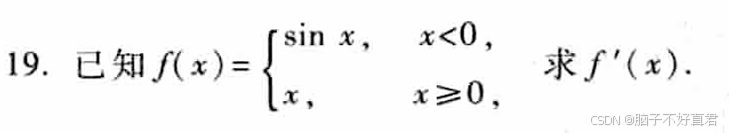
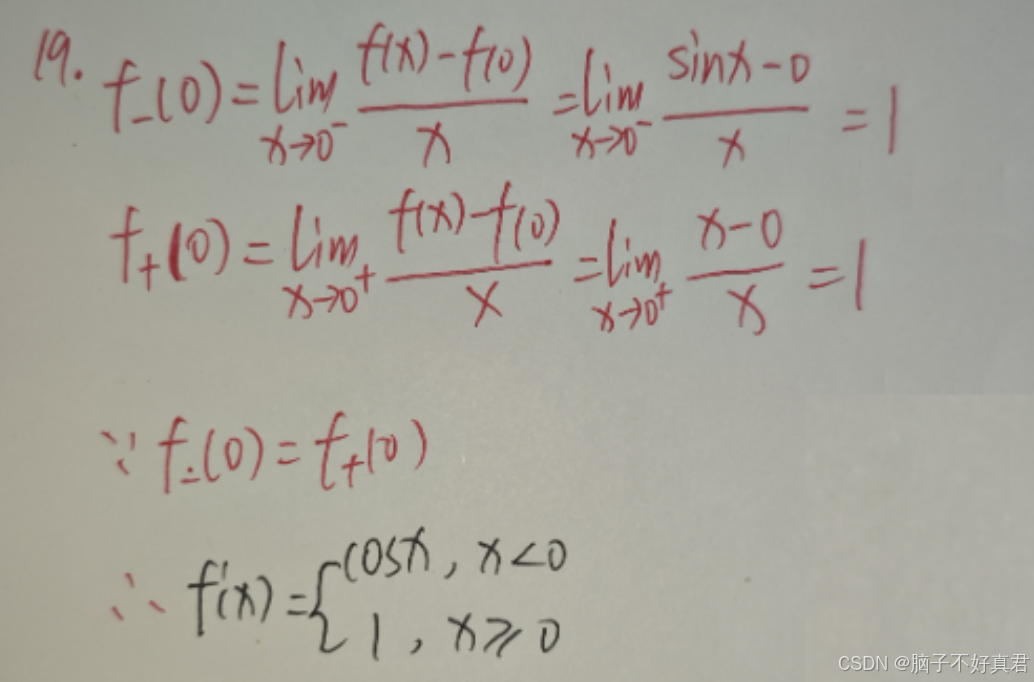
20.

参考资料

高等数学·上册 第七版 (同济大学数学系)
高等数学 同济第七版 上册 习题辅导书 -- 常桂娟 -- 2015 -- 电子工业出版社
导数表_百度百科
openGL中关于顶点的法线、切线、副切线-CSDN博客