自相关函数学习思考

自相关（Autocorrelation），也叫序列相关，是一个信号与其自身在不同时间点的互相关。非正式地来说，自相关是对同一信号在不同时间的两次观察，通过对比来评判两者的相似程度。自相关函数就是信号$x(t)$和它的时移信号$x(t-\tau )$的乘积平均值。它是时移变量τ的函数。

也就是说一个函数$f(t)$的自相关函数为::
$$R(\tau )={\int }_{-\infty }^{+\infty }f(t)f(t-\tau )dt$$
假设$f(t)$是周期$T=\frac{2\pi }{w}$无穷大的周期函数，那么$R(\tau )$可以写成周期积分:

$$R(\tau )={\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}f(t)f(t-\tau )dt$$

根据傅里叶级数的原理，$f(t)$可以写成傅里叶级数的形式：
$$f(t)=A_0+\sum _{n=1}^{\infty }{A}_{n}sin(nwt+{\psi }_n),(1)$$
$f(t-\tau )$则可以写成
$$f(t-\tau )=A_0+\sum _{n=1}^{\infty }{A}_{n}sin(nwt-nw\tau +{\psi }_n),(2)$$

因此${\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}f(t)f(t-\tau )dt$，可以分解成从(1)和(2)式中任意抽取两个项相乘后积分再求和，有下面四种情况：

• 两个抽取都是直流项
  ${\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}{A}_0\ast A_{0}dt=\frac{2\pi }{w}{A}_0^2$
• 一个抽取是直流项，另一个抽取是交流项
  ${\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}{A}_0\ast A_{n}sin(nwt-nw\tau +{\psi }_n)dt=-\frac{A_0{A}_n}{nw}cos(nwt-nw\tau +{\psi }_n){|}_{-\frac{\pi }{w}}^{\frac{\pi }{w}}=0$
  ${\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}{A}_0\ast A_{n}sin(nwt+{\psi }_n)dt=-\frac{A_0{A}_n}{nw}cos(nwt+{\psi }_n){|}_{-\frac{\pi }{w}}^{\frac{\pi }{w}}=0$
• 两个抽取都是交流项，但n不相同
  $$\begin{array}{rl}sin(n_{a}wt+{\psi }_{n_a})sin(n_{b}wt-n_{b}w\tau +{\psi }_{n_b})& =\\ & =\frac{1}{2}\left(cos(n_{a}wt+{\psi }_{n_a}-n_{b}wt+n_{b}w\tau -{\psi }_{n_b})-cos(n_{a}wt+{\psi }_{n_a}+n_{b}wt-n_{b}w\tau +{\psi }_{n_b})\right)\\ & =\frac{1}{2}\left(cos((n_a-n_b)wt+n_{b}w\tau +{\psi }_{n_a}-{\psi }_{n_b})-cos((n_a+n_b)wt-n_{b}w\tau +{\psi }_{n_a}+{\psi }_{n_b})\right)\end{array}$$

$$\begin{array}{rl}{\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}{A}_{n_a}{A}_{n_b}sin(n_{a}wt+{\psi }_{n_a})sin(n_{b}wt-n_{b}w\tau +{\psi }_{n_b})dt& =\\ & ={\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}\frac{1}{2}{A}_{n_a}{A}_{n_b}\left(cos((n_a-n_b)wt+n_{b}w\tau +{\psi }_{n_a}-{\psi }_{n_b})-cos((n_a+n_b)wt-n_{b}w\tau +{\psi }_{n_a}+{\psi }_{n_b})\right)dt\\ & =\frac{1}{2}{A}_{n_a}{A}_{n_b}\left(\frac{1}{(n_a-n_b)w}sin((n_a-n_b)wt+n_{b}w\tau +{\psi }_{n_a}-{\psi }_{n_b}){|}_{-\frac{\pi }{w}}^{\frac{\pi }{w}}-\frac{1}{(n_a+n_b)w}sin((n_a+n_b)wt-n_{b}w\tau +{\psi }_{n_a}+{\psi }_{n_b}){|}_{-\frac{\pi }{w}}^{\frac{\pi }{w}}\right)\\ & =0\end{array}$$

• 两个抽取都是交流项，但n相同
  $$\begin{array}{rl}{\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}{A}_{n_a}{A}_{n_b}sin(n_{a}wt+{\psi }_{n_a})sin(n_{b}wt-n_{b}w\tau +{\psi }_{n_b})dt& =\\ & ={\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}\frac{1}{2}{A}_{n_a}{A}_{n_b}\left(cos((n_a-n_b)wt+n_{b}w\tau +{\psi }_{n_a}-{\psi }_{n_b})-cos((n_a+n_b)wt-n_{b}w\tau +{\psi }_{n_a}+{\psi }_{n_b})\right)dt\\ & =\frac{1}{2}{A}_n^2\left(cos(nw\tau ){|}_{-\frac{\pi }{w}}^{\frac{\pi }{w}}-\frac{1}{2nw}sin(2nwt-nw\tau +2{\psi }_n){|}_{-\frac{\pi }{w}}^{\frac{\pi }{w}}\right)\\ & =\frac{1}{2}{A}_n^2\left(\frac{2\pi }{w}cos(nw\tau )-0\right)\\ & =\frac{\pi }{w}{A}_n^{2}cos(nw\tau )\end{array}$$
  综合四种情况可知:
  $${\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}f(t)f(t-\tau )dt=\frac{2\pi }{w}{A}_0^2+\frac{\pi }{w}\sum _{n=1}^{\infty }{A}_n^{2}cos(nw\tau )$$
  由(3)式可知，在$\tau =0$时，自相关函数$R(\tau )$有最大值$\frac{2\pi }{w}{A}_0^2+\frac{\pi }{w}{\sum }_{n=1}^{\infty }{A}_n^2$

如果$f(t)$是只包含交流分量的函数，在频域上是一条幅值为$I$的直线(从$n_a$到$n_b$)，那么这样的$f(t)$自相关函数可以进一步进行化简:
$$\begin{array}{rl}R(\tau )& ={\int }_{-\frac{\pi }{w}}^{\frac{\pi }{w}}f(t)f(t-\tau )dt\\ & =\frac{2\pi }{w}{A}_0^2+\frac{\pi }{w}\sum _{n=1}^{\infty }{A}_n^{2}cos(nw\tau )\\ & =\frac{\pi }{w}\sum _{n_a}^{n_b}{I}^{2}cos(nw\tau )\\ & \approx \frac{\pi }{w}{I}^2{\int }_{n_a}^{n_b}cos(nw\tau )dn\\ & \approx \frac{\pi }{w}{I}^2\frac{sin(nw\tau )}{w\tau }{|}_{n_a}^{n_b}\\ & \approx \frac{\pi }{w}{I}^2\frac{(sin(n_{b}w\tau )-sin(n_{a}w\tau ))}{w\tau }\\ & \approx \frac{\pi }{w}{I}^2\frac{(sin(\frac{n_a+n_b}{2}w\tau +\frac{n_b-n_a}{2}w\tau )-sin(\frac{n_a+n_b}{2}w\tau -\frac{n_b-n_a}{2}w\tau ))}{w\tau }\\ & \approx \frac{\pi }{w}{I}^2\frac{2cos(\frac{n_a+n_b}{2}w\tau )sin(\frac{n_b-n_a}{2}w\tau )}{w\tau }\\ & \approx \frac{T}{2}(n_b-n_a)I^2\frac{cos(\frac{n_a+n_b}{2}w\tau )sin(\frac{n_b-n_a}{2}w\tau )}{\frac{n_b-n_a}{2}w\tau }....(4)\end{array}$$

观察(4)式可以发现，$cos(\frac{n_a+n_b}{2}w\tau )$振动速度比$sin(\frac{n_b-n_a}{2}w\tau )$要快，
而且$\frac{sin(\frac{n_b-n_a}{2}w\tau )}{\frac{n_b-n_a}{2}w\tau }$是除着$\tau$增大，按$\frac{n_b-n_a}{2}w\tau$倒数衰减的正弦波形。
所以，$R(\tau )$在原函数是宽带频率函数时，其波形是衰减的较慢正弦波形乘以一个比较快的余弦波。

用ipython进行验证:

import numpy as np
import matplotlib.pyplot as plt
import math

%matplotlib inline

N = 512
spectral = [0j] * N

na=100
nb=120

for i in range(N):
    if na<=i<=nb:
        spectral[i] = (1+0j) * N / 2 #由于 ifft是用X(k)=N * Amp N倍幅值计算的 所以要乘以N 除以2是正负频各分一半幅值
    if N - nb <=i<= N - na:
        spectral[i] = (1+0j) * N / 2

inputwave = np.fft.ifft(spectral)
inputwave = np.real(inputwave)

R_wave = [0]*N

for tau in range(N):
    sumt = 0
    for i in range(N):
        temp = i - tau
        sumt = sumt + inputwave[i] * inputwave[temp] #自相关函数
    R_wave[tau] = sumt 
    
approxR_wave = [0]*N    #近似计算的自相关波形
nc = (na+nb)/2
dn = (nb-na)/2
amp = N * (nb-na) * 1**2 / 2
for i in range(1,N):
    tau = i
    if i > N/2:
        tau = N - i  #相移不能大于半周期，大于相当于是负相移
    psi =  nc * tau * 2 * math.pi / N
    cositem = math.cos(psi)
    psi =  dn * tau * 2 * math.pi / N
    sinitem = math.sin(psi)
    approxR_wave[i] = amp * cositem * sinitem / psi
    
approxR_wave[0] = amp
    
plt.figure(figsize=(15,10))
plt.plot(R_wave)
plt.plot(approxR_wave)

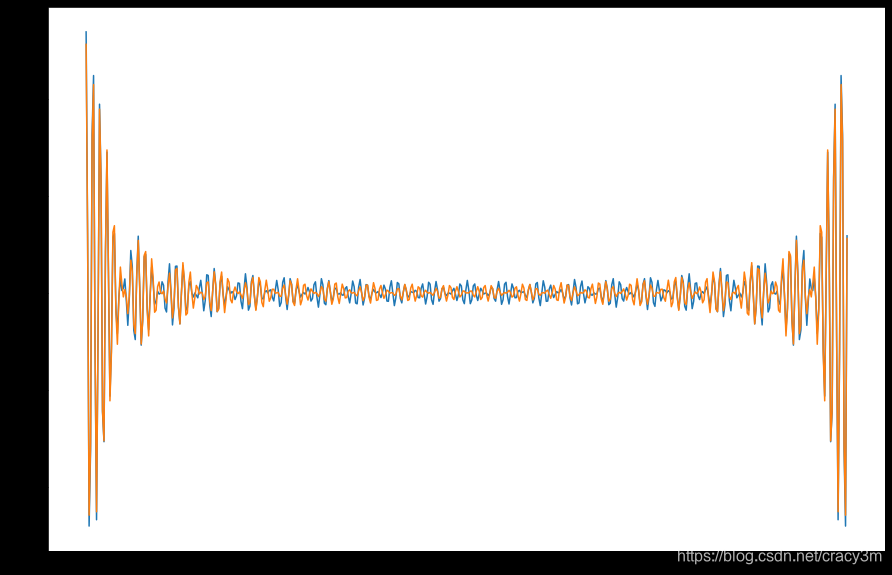
如果$f(t)$是频域正态分布的宽带信号呢？
用ipython进行试验，看看波形

sigma = 5 #标准差 
mu = (na + nb) / 2  #期望（均数）

for i in range(N):
    if na<=i<=nb:
        temp = (i-mu)/sigma
        temp = temp ** 2
        temp = temp / 2
        temp = math.exp(-temp)
        temp = temp/(math.sqrt(2 * math.pi)*sigma)
        spectral[i] = temp * (1+0j) * N / 2 #由于 ifft是用X(k)=N * Amp N倍幅值计算的 所以要乘以N 除以2是正负频各分一半幅值
    if N - nb <=i<= N - na:
        temp = (i- N +mu)/sigma
        temp = temp ** 2
        temp = temp / 2
        temp = math.exp(-temp)
        temp = temp/(math.sqrt(2 * math.pi)*sigma)
        spectral[i] = temp*(1+0j) * N / 2

inputwave = np.fft.ifft(spectral)
inputwave = np.real(inputwave)

R_wave1 = [0]*N

for tau in range(N):
    sumt = 0
    for i in range(N):
        temp = i - tau
        sumt = sumt + inputwave[i] * inputwave[temp] #自相关函数
    R_wave1[tau] = sumt

plt.figure(figsize=(15,10))
plt.plot(np.abs(spectral))
plt.figure(figsize=(15,10))
plt.plot(R_wave)
plt.figure(figsize=(15,10))
plt.plot(R_wave1)

有正态分布的宽带频域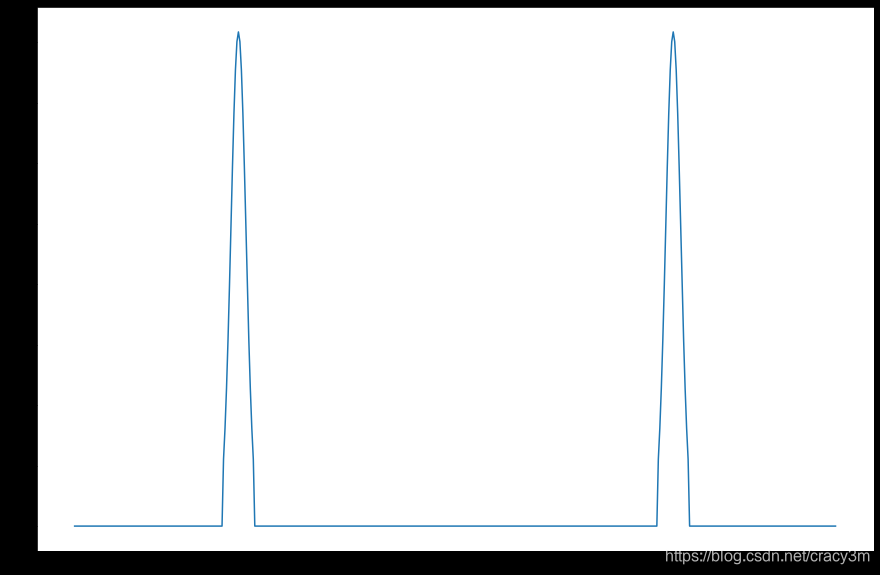

直线分布的宽带频域自相关时域波形

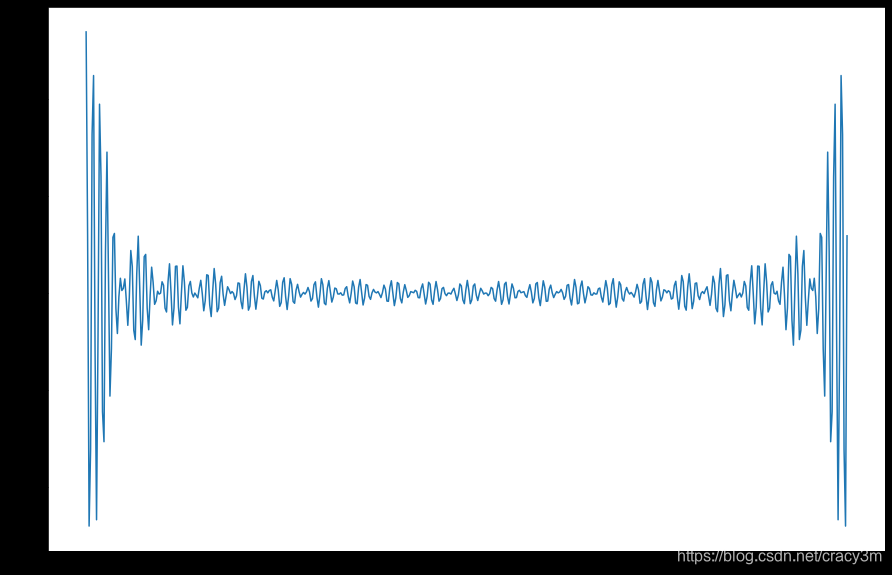
正态分布的宽带频域自相关时域波形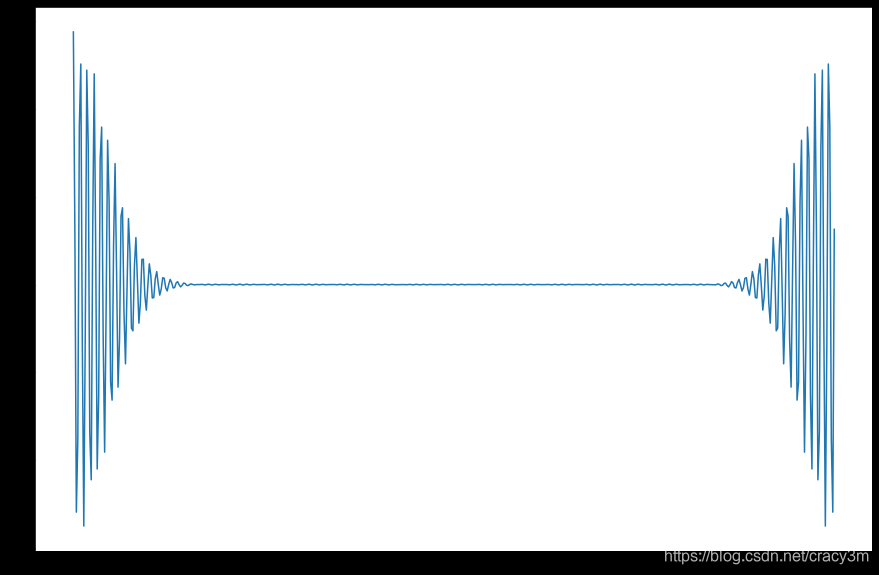

对比可以看到，正态分布的自相关函数波形中间杂波小得多，而且振动的频率分量更少一些(向中心频率靠，相当于做了滤波)