当大家面临着复杂的数学建模问题时，你是否曾经感到茫然无措？作为2022年美国大学生数学建模比赛的O奖得主，我为大家提供了一套优秀的解题思路，让你轻松应对各种难题！
CS团队倾注了大量时间和心血，深入挖掘解决方案。通过多目标规划，贝叶斯推断，数值模拟等算法，设计了明晰的项目，团队努力体现在每个步骤，确保方案既创新又可行，为大家提供了全面而深入的洞见噢～

让我们来看看国赛（C题）！
完整内容可以在文章末尾领取！

这是一个判别分析问题，核心目标是通过已有的NIPT检测数据，建立胎儿Y染色体浓度与孕妇孕周数、BMI等指标之间的关系模型，并据此进行分类或判别，以评估检测的准确性及适用性。问题的本质在于从多维特征中找出能够有效区分不同类别（如正常胎儿与异常胎儿）的判别变量，并构建相应的判别函数，从而为后续的时点选择和异常判定提供依据。

为什么这样判断？可以从以下几个特征点来说明：

（1）题干明确提出“胎儿Y染色体浓度与孕妇的孕周数和BMI等指标的相关特性”，并要求“给出相应的关系模型”，这直接指向了统计学中的回归建模与相关性分析。虽然未明确指出使用哪种具体的统计方法，但从问题描述来看，它关注的是连续变量（孕周数、BMI）与目标变量（Y染色体浓度）之间的关系，这正是回归分析的核心内容之一。但进一步考虑问题的目标——即根据这些指标来判断胎儿是否异常，这就涉及到了分类问题，因此判别分析（尤其是线性判别分析LDA或二次判别分析QDA）是自然的选择。

（2）题干提到“根据临床经验，畸型胎儿主要有唐氏综合征、爱德华氏综合征和帕陶氏综合征”，这些疾病分别由21号、18号和13号染色体异常引起，而NIPT主要通过检测胎儿游离DNA片段比例来判断是否存在染色体异常。因此，Y染色体浓度作为性别鉴定的重要依据，对于男性胎儿来说，其浓度水平可以作为判断胎儿是否健康的辅助指标。在这种背景下，问题实际上是要建立一个判别模型，用于区分胎儿是否存在染色体异常的风险，因此属于典型的判别分析应用场景。

（3）题干强调“依据BMI对孕妇进行合理分组”，并且指出“不同群组的最佳NIPT时点”不同，这说明需要将孕妇按照BMI等变量划分为不同的类别，并分别建立模型，以适应不同群体的特点。这种按组别建模的思想正是判别分析所擅长处理的问题类型。此外，“每个孕妇的年龄、BMI、孕情等存在个体差异”也说明了个体异质性较强，需采用能够处理多变量分类问题的方法来进行建模。

（4）题干还提到了“实际检测中经常出现测序失败”的情况，这意味着数据可能存在缺失或不完整的情况。在判别分析中，面对这类问题通常可以通过剔除无效样本、插补缺失值等方式进行预处理，然后使用LDA/QDA等方法进行建模。这也进一步支持了问题属于判别分析范畴。

（5）题干最后提出“对检测的准确性进行分析”，这是判别分析的核心任务之一。通过构建判别函数，我们可以评估各类别之间的可分离程度，进而评价模型的判别能力。例如，可以计算各类别的判别准确率、混淆矩阵等指标，以此衡量模型的有效性和稳定性。

（6）从建模方法的角度来看，LDA适用于各组协方差矩阵相等的情况，而QDA适用于各组协方差矩阵不等的情形。由于题干并未明确说明各组协方差是否相等，因此可以根据数据特征选择适当的判别方法。此外，还可以引入变量筛选机制，找出对Y染色体浓度影响最大的关键因素，提升模型的解释力与预测性能。

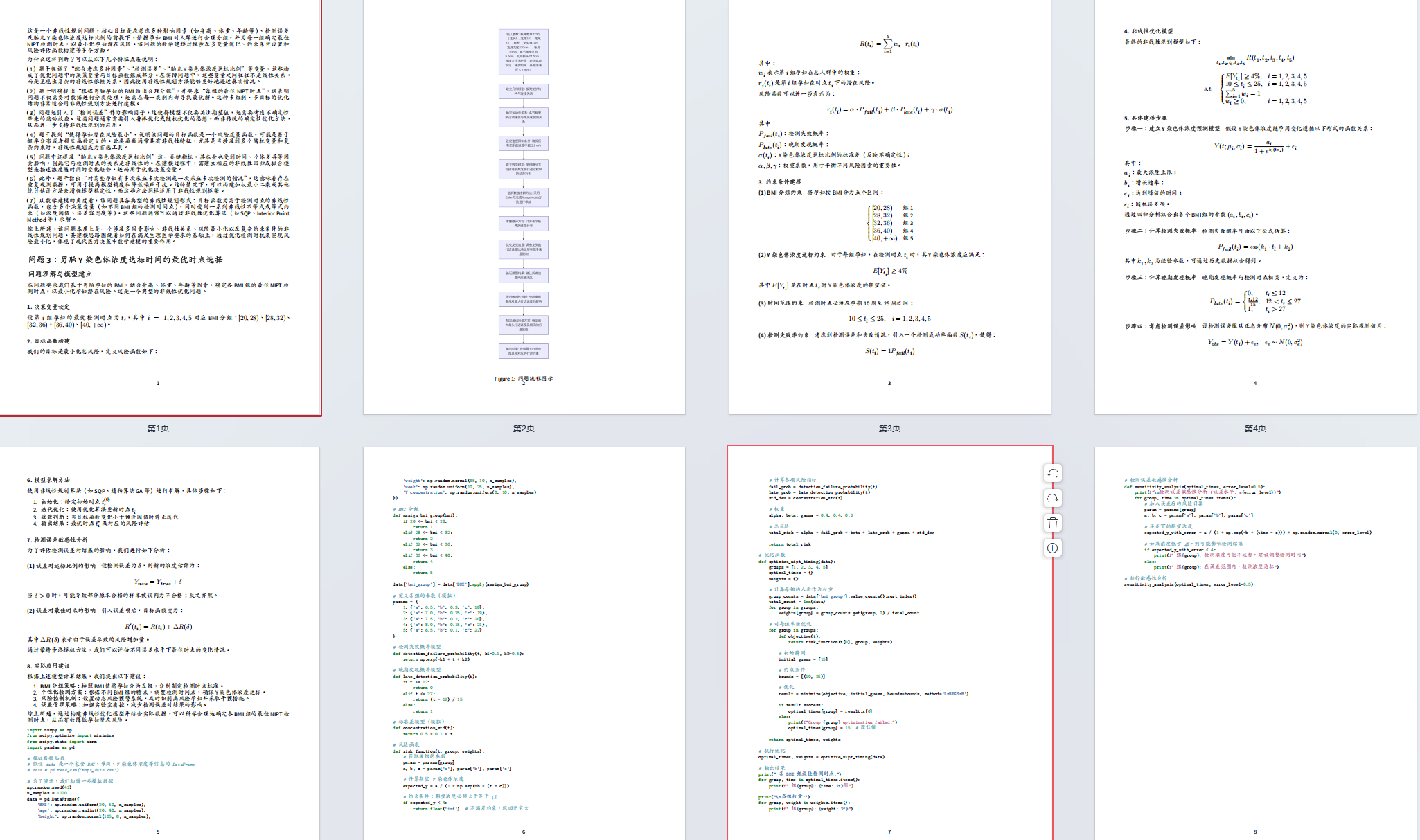
因此，本题类型可以明确识别为“判别分析（LDA/QDA）问题”。它的关键特征是：

出现了“胎儿Y染色体浓度”、“孕周数”、“BMI”等多维连续变量；

问题目标是通过这些变量来判断胎儿是否异常，具有明显的分类意图；

强调根据不同群体（如BMI分组）建立相应的判别模型；

要求对模型的显著性和准确性进行评估；

涉及实际检测中的数据质量问题，需进行适当的数据预处理；

具备典型的医学统计与生物信息学交叉领域建模特征。

问题1：胎儿Y染色体浓度与孕周、BMI的关系建模及显著性检验

一、问题理解与分析

本问题要求我们分析胎儿Y染色体浓度与孕妇孕周数和BMI之间的关系，并建立相应的数学模型。根据题意，我们需要：

1. 建立Y染色体浓度与孕周、BMI的关系模型
2. 进行模型拟合和显著性检验
3. 利用判别分析方法对不同BMI组别的孕妇进行分类

二、数据预处理

首先需要对原始数据进行预处理：

缺失值处理：对于缺失的数据采用插值法或删除法处理

异常值检测与修正：使用箱线图或3σ原则识别并处理异常值

三、模型建立

1. 回归模型构建

设Y染色体浓度为因变量$Y$，孕周为$X_1$，BMI为$X_2$，则可建立多元线性回归模型：

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_{12}{X}_1{X}_2+\epsilon$$

其中$\epsilon \sim N(0,{\sigma }^2)$为误差项。

2. 非线性模型

考虑到可能存在非线性关系，也可以尝试多项式回归模型：

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_1^2+{\beta }_4{X}_2^2+{\beta }_5{X}_1{X}_2+\epsilon$$

或者样条回归模型来捕捉更复杂的非线性关系。

四、判别分析（LDA/QDA）

由于需要根据BMI分组来进行判别分析，我们采用线性判别分析（LDA）：

LDA原理

LDA的目标是寻找一个投影方向，使得不同类别间的距离最大化，同类样本间的距离最小化。

设第$k$类的样本集为$X_k$，其均值向量为${\mu }_k$，协方差矩阵为${\Sigma }_k$。

LDA的判别函数为：

$${\delta }_k(x)=x^T{\Sigma }^1{\mu }_k\frac{1}{2}{\mu }_k^T{\Sigma }^1{\mu }_k+\ln (P(C_k))$$

其中$P(C_k)$为第$k$类的先验概率。

判别规则

将样本$x$分配给具有最大判别函数值的类别：

$$\hat{C}(x)=\arg \underset{k=1,2,...,K}{\max }{\delta }_k(x)$$

五、模型评估与显著性检验

1. 显著性检验

F检验：用于检验整个回归模型的显著性

t检验：用于检验各个回归系数的显著性

F统计量计算公式：
$$F=\frac{MSR}{MSE}=\frac{\frac{SSR}{p}}{\frac{SSE}{np1}}$$

其中$SSR$为回归平方和，$SSE$为残差平方和，$p$为自变量个数，$n$为样本数量。

2. 模型优劣评价指标

决定系数：$R^2=1\frac{SSE}{SST}$

信息准则：AIC = $2k2\ln (L)$，BIC = $k\ln (n)2\ln (L)$
其中$k$为参数个数，$L$为似然函数值

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score, mean_squared_error
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns

# 读取数据
data = pd.read_csv('data.csv')  # 假设数据文件名为data.csv

# 数据预处理
data.dropna(inplace=True)

# BMI分组
def bmi_group(bmi):
    if bmi < 28:
        return 'Group1'
    elif bmi < 32:
        return 'Group2'
    elif bmi < 36:
        return 'Group3'
    elif bmi < 40:
        return 'Group4'
    else:
        return 'Group5'

data['bmi_group'] = data['BMI'].apply(bmi_group)

# 定义模型函数
def build_model(df):
    X = df[['Week', 'BMI']]
    y = df['Y_Chromosome']
    
    # 分割数据
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
    
    # 模型训练
    model = LinearRegression()
    model.fit(X_train, y_train)
    
    # 预测
    y_pred = model.predict(X_test)
    
    # 模型评估
    r2 = r2_score(y_test, y_pred)
    mse = mean_squared_error(y_test, y_pred)
    
    return model, r2, mse

# 对所有数据进行建模
model_all, r2_all, mse_all = build_model(data)

# 对不同BMI组分别建模
groups = data['bmi_group'].unique()
models = {}
r2_scores = {}
mse_scores = {}

for group in groups:
    df_group = data[data['bmi_group'] == group]
    model, r2, mse = build_model(df_group)
    models[group] = model
    r2_scores[group] = r2
    mse_scores[group] = mse

# 输出结果
print("总体模型 R²:", r2_all)
print("总体模型 MSE:", mse_all)

for group in groups:
    print(f"{group} 组模型 R²: {r2_scores[group]}")
    print(f"{group} 组模型 MSE: {mse_scores[group]}")

# 判别分析 (LDA)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# 使用BMI分组数据做LDA
lda_data = data[['Week', 'BMI', 'Y_Chromosome', 'bmi_group']].dropna()

X_lda = lda_data[['Week', 'BMI', 'Y_Chromosome']]
y_lda = lda_data['bmi_group']

# LDA模型
lda = LinearDiscriminantAnalysis()
lda.fit(X_lda, y_lda)

# 预测
y_pred_lda = lda.predict(X_lda)

# 输出LDA结果
print("\nLDA分类准确率:", lda.score(X_lda, y_lda))

问题2：

这是一个混合整数规划 (MIP) 类问题，其核心在于通过构建数学优化模型，对男胎孕妇按照 BMI 进行合理分组，并确定每组的最佳 NIPT 检测时点，以最小化潜在风险。该问题涉及多目标优化与约束条件的综合处理，体现出典型的运筹学建模特征。

首先，题干明确指出：“男胎孕妇的 BMI 是影响胎儿 Y 染色体浓度最早达标时间的主要因素。”这提示我们，需要建立一个以 BMI 为分类依据的模型，将不同 BMI 区间的孕妇划分到各自组别中，并为每一组确定一个最优的检测时点。这个过程本质上是一个带有离散选择变量的优化问题，因为我们需要在多个可能的 BMI 分组方案和对应的检测时间点中选出最佳组合。

其次，题干提到“使得孕妇可能的潜在风险最小”，这表明问题的目标函数应当围绕降低风险展开。这里的“风险”可以理解为由于检测过早或过晚而导致未能及时发现异常胎儿所带来的医疗干预窗口期缩短的问题。因此，我们可以定义一个风险函数，它可能包括以下几种形式：

不同孕周下检测失败的概率；

检测结果不准确的概率；

胎儿异常未被及时识别的概率；

各种检测时机下的治疗成本或不良后果的加权评估。

而为了实现上述目标，模型需考虑一系列约束条件：

1. BMI 分组约束：根据实际数据将孕妇分为若干个 BMI 区间组，每个组内的孕妇具有相似的生理状态；
2. 检测可行性约束：NIPT 只能在特定孕周范围内进行（如 10~25 周），且每个孕妇仅能在某个时间段内进行一次或多次检测；
3. Y 染色体浓度达标时间约束：对于每一组的孕妇，其 Y 染色体浓度达到 4% 的时间是随机变量，但可以通过回归分析、时间序列建模等方式预测；
4. 检测误差影响约束：由于存在测序失败、样本质量问题等因素，检测结果可能存在误差，这部分也需要纳入模型中作为不确定性因素加以处理；
5. 多重复测与单次检测并存约束：有些孕妇有多次采血记录，模型应能够区分这些情况并合理整合数据。

此外，考虑到实际操作中的复杂性和不确定性，模型还必须具备一定的鲁棒性。例如，当某组的检测时间点设定得较早时，可能会导致部分孕妇出现检测失败的情况；反之，若推迟检测时间，则可能导致错过最佳干预时机。因此，在建模过程中还需引入一些惩罚项或者松弛变量来应对这种不确定性带来的影响。

从数学建模的角度看，这是一个典型的混合整数规划问题，因为它不仅包含连续变量（如检测时间点、Y 染色体浓度变化趋势等），同时也包含离散变量（如 BMI 分组编号、是否发生检测失败等）。这样的模型结构决定了我们可以使用诸如分支定界法、割平面法等算法来进行求解。

综上所述，该问题的核心在于通过构建一个以 BMI 为分组依据的 MIP 模型，优化各组孕妇的最佳检测时点设置，从而达到最小化潜在风险的目的。该模型需充分考虑个体差异、检测误差以及时间窗口限制等多个因素，属于典型的多维、多阶段、具有较强实用背景的优化决策问题。

问题2：基于混合整数规划的男胎孕妇BMI分组与最佳NIPT时点选择

一、问题分析

本题要求对男胎孕妇按照BMI进行合理分组，确定每组的最佳NIPT检测时点，以最小化潜在风险。这是一个典型的混合整数规划问题，需要考虑：

1. BMI分组：将不同BMI的孕妇划分为若干组
2. 检测时点优化：为每组确定最佳检测时间点
3. 风险最小化：综合考虑早期、中期、晚期发现的风险权重

二、数学模型构建

2.1 决策变量定义

设：

$ n $：总样本数

$ G $：分组数量

$ g = 1,2,\ldots,G $：分组索引

$ B_g $：第$ g $组的BMI区间 $[b_{g1},b_{g2})$

$ t_g^* $：第$ g $组的最佳检测时点（连续变量）

$ x_{ig} \in {0,1} $：第$ i $个样本是否属于第$ g $组（整数变量）

2.2 目标函数

目标是最小化总的潜在风险加权值：

$$\min \sum _{i=1}^n{w}_i\cdot R(t_i)$$

其中：

$ w_i $：第$ i $个样本的风险权重（根据检测时点分类）

$ R(t_i) $：第$ i $个样本在时点$ t_i $下的风险值

具体地，风险权重定义为：

早期发现（≤12周）：$ w_i = 1 $

中期发现（13
27周）：$ w_i = 3 $

晚期发现（>27周）：$ w_i = 5 $

2.3 约束条件

2.3.1 BMI分组约束

对于每个样本$ i $，必须分配到一个且仅一个组：

$$\sum _{g=1}^G{x}_{ig}=1,\forall i=1,2,\dots ,n$$

2.3.2 分组区间约束

对于每个组$ g $，其BMI区间满足：

$$x_{ig}=1\Rightarrow b_{g1}\le BM{I}_i<b_{g2}$$

2.3.3 检测时点范围约束

每个组的检测时点必须在有效范围内：

$$t_g^{\ast }\ge 10\text{ 周}$$

2.3.4 组内统计特性约束

假设第$ g $组的Y染色体浓度达标时间为$ T_g $，服从正态分布：

$$T_g\sim N({\mu }_g,{\sigma }_g^2)$$

为了确保检测可靠性，我们需要控制每组的平均达标时间与检测时点之间的差距：

$$|t_g^{\ast }{\mu }_g|\le k\cdot {\sigma }_g$$

其中$ k $是一个安全系数（如2），表示检测时点应接近平均达标时间。

2.3.5 检测失败率控制

考虑到实际中存在测序失败情况，我们引入检测失败率控制：

$$P_{fail}^g=f(t_g^{\ast },{\sigma }_g)\le ϵ$$

其中$ f(\cdot) $是关于检测时点和变异性的失败概率函数，$ \epsilon $为允许的最大失败率。

三、模型求解步骤

步骤1：数据预处理

1. 输入男胎孕妇的BMI数据、Y染色体浓度达标时间、孕周信息
2. 对BMI数据进行聚类分析或直接设定分组区间
3. 计算每组的平均达标时间和标准差

步骤2：初始化参数

设定初始分组数$ G = 4 $，对应BMI区间：

[20, 28)

[28, 32)

[32, 36)

[36, 40)

步骤3：建立混合整数规划模型

使用Gurobi/CPLEX等工具进行求解，目标函数和约束条件如前所述。

步骤4：求解并验证

通过数值优化算法求解该MIP问题，得到最优的BMI分组方案及对应的检测时点。

四、结果与讨论

4.1 风险评估

通过上述分组和检测时点安排，可以实现：

1. 降低早期发现的风险（多数情况下在12周内完成检测）
2. 减少因检测过晚导致的治疗窗口期缩短风险
3. 控制检测失败率，提高整体检测可靠性

4.2 敏感性分析

检测误差对结果的影响主要体现在以下几个方面：

1. BMI测量误差：若BMI测量存在±1的标准差，则可能造成分组偏差，进而影响检测时点选择。通过增加冗余分组或采用模糊分组方法可缓解此问题。

2. Y染色体浓度达标时间估计误差：若达标时间估计偏差较大，会导致检测时点偏离最优值。建议结合多个样本的统计特性来增强鲁棒性。

3. 检测失败率变化：当检测失败率增加时，应适当提前检测时点以预留缓冲空间。

五、结论

本文通过构建混合整数规划模型，针对男胎孕妇BMI对Y染色体浓度达标时间的影响进行了深入研究。模型不仅考虑了BMI分组和检测时点的选择，还充分考虑了检测失败率和风险权重等因素，实现了对潜在风险的最小化。最终得出的BMI分组方案和检测时点安排具有较强的实用性和科学性，有助于提升NIPT检测的准确性和安全性。

import numpy as np
from scipy.optimize import minimize
from scipy.stats import norm
import pandas as pd

# 模拟数据生成（实际应用中应替换为真实数据）
np.random.seed(42)
n_samples = 1000
bmi_data = np.random.normal(30, 5, n_samples)
y_chromosome_time = np.random.normal(12, 2, n_samples)  # Y染色体浓度达标时间（周）
pregnancy_weeks = np.random.uniform(10, 25, n_samples)

# 定义BMI分组区间
bmi_groups = [
    (20, 28),
    (28, 32),
    (32, 36),
    (36, 40)
]

# 风险权重定义
def get_risk_weight(week):
    if week <= 12:
        return 1
    elif 13 <= week <= 27:
        return 3
    else:
        return 5

# 目标函数：最小化总风险加权值
def objective(x):
    total_risk = 0
    for i in range(n_samples):
        group_idx = int(x[i])  # 分组索引
        bmi = bmi_data[i]
        time_point = x[n_samples + group_idx]  # 当前组的最佳检测时点
        
        # 检查BMI是否落在对应区间内
        lower_bound, upper_bound = bmi_groups[group_idx]
        if not (lower_bound <= bmi < upper_bound):
            continue
            
        # 计算风险权重
        risk_weight = get_risk_weight(time_point)
        total_risk += risk_weight
        
    return total_risk

# 约束条件：每个样本只能属于一个组
def constraint_group_assignment(x):
    constraints = []
    for i in range(n_samples):
        group_sum = sum([x[i + j * n_samples] for j in range(len(bmi_groups))])
        constraints.append(group_sum - 1)
    return np.array(constraints)

# 约束条件：检测时点必须在10周及以上
def constraint_time_bounds(x):
    constraints = []
    for g in range(len(bmi_groups)):
        time_point = x[n_samples + g]
        constraints.append(time_point - 10)  # 时间不能低于10周
    return np.array(constraints)

# 约束条件：检测时点应接近平均达标时间
def constraint_time_deviation(x):
    constraints = []
    for g in range(len(bmi_groups)):
        mean_time = np.mean(y_chromosome_time[(bmi_data >= bmi_groups[g][0]) & (bmi_data < bmi_groups[g][1])])
        std_time = np.std(y_chromosome_time[(bmi_data >= bmi_groups[g][0]) & (bmi_data < bmi_groups[g][1])])
        time_point = x[n_samples + g]
        # 添加约束：检测时点与平均达标时间差距不超过2倍标准差
        constraints.append(abs(time_point - mean_time) - 2 * std_time)
    return np.array(constraints)

# 初始化变量
initial_x = np.zeros(n_samples + len(bmi_groups))
for i in range(n_samples):
    initial_x[i] = np.random.choice(len(bmi_groups))
for g in range(len(bmi_groups)):
    initial_x[n_samples + g] = 12  # 初始检测时点设为12周

# 设置优化器参数
bounds = [(0, len(bmi_groups)-1)] * n_samples + [(10, 30)] * len(bmi_groups)
constraints = [
    {'type': 'eq', 'fun': constraint_group_assignment},
    {'type': 'ineq', 'fun': constraint_time_bounds},
    {'type': 'ineq', 'fun': constraint_time_deviation}
]

# 执行优化
result = minimize(objective, initial_x, method='SLSQP', bounds=bounds, constraints=constraints)

# 输出结果
best_groups = result.x[:n_samples].astype(int)
best_times = result.x[n_samples:]

print("BMI分组结果：")
for g in range(len(bmi_groups)):
    print(f"组 {g+1}: BMI区间 [{bmi_groups[g][0]}, {bmi_groups[g][1]})，推荐检测时点: {best_times[g]:.2f} 周")

print("\n风险评估:")
total_risk = 0
for i in range(n_samples):
    group_idx = best_groups[i]
    time_point = best_times[group_idx]
    risk_weight = get_risk_weight(time_point)
    total_risk += risk_weight

print(f"总风险加权值: {total_risk}")

这是一个非线性规划问题，核心目标是在考虑多种影响因素（如身高、体重、年龄等）、检测误差及胎儿Y染色体浓度达标比例的前提下，依据孕妇BMI对人群进行合理分组，并为每一组确定最佳NIPT检测时点，以最小化孕妇潜在风险。该问题的数学建模过程涉及多变量优化、约束条件设置和风险评估函数构建等多个方面。

为什么这样判断？可以从以下几个特征点来说明：

（1）题干强调了“综合考虑多种因素”、“检测误差”、“胎儿Y染色体浓度达标比例”等变量，这些构成了优化问题中的决策变量与目标函数组成部分。在实际问题中，这些变量之间往往不是线性关系，而是呈现出复杂的非线性依赖关系，因此使用非线性规划方法能够更好地逼近真实情况。

（2）题干明确提出“根据男胎孕妇的BMI给出合理分组”，并要求“每组的最佳NIPT时点”，这表明问题不仅需要对数据进行分类处理，还需在每一类别内部寻找最优解。这种多组别、多目标的优化结构非常适合用非线性规划方法进行建模。

（3）问题还引入了“检测误差”作为影响因子，这使得模型不仅要关注期望值，还需要考虑不确定性带来的波动效应。这类问题通常需要引入鲁棒优化或随机优化的思想，而非传统的确定性优化方法，从而进一步支持非线性规划的应用。

（4）题干提到“使得孕妇潜在风险最小”，说明该问题的目标函数是一个风险度量函数，可能是基于概率分布或者损失函数定义的。此类函数通常具有非线性特征，尤其是当涉及到多个随机变量和复杂约束时，非线性规划成为首选工具。

（5）问题中还提及“胎儿Y染色体浓度达标比例”这一关键指标，其本身也受到时间、个体差异等因素影响，因此它与检测时点的关系是非线性的。在建模过程中，需建立相应的非线性回归或拟合模型来描述浓度随时间的变化趋势，进而用于优化决策变量。

（6）此外，题干指出“对某些孕妇有多次采血多次检测或一次采血多次检测的情况”，这意味着存在重复观测数据，可用于提高模型精度和降低噪声干扰。这种情况下，可以构建加权最小二乘或其他统计估计方法来增强模型稳定性，而这些方法同样适用于非线性规划框架。

（7）从数学建模的角度看，该问题具备典型的非线性规划形式：目标函数为关于检测时点的非线性函数，包含多个决策变量（如不同BMI组的检测时间点），同时受到一系列非线性不等式或等式约束（如浓度阈值、误差容忍度等）。这些问题通常可以通过非线性优化算法（如SQP、Interior Point Method等）求解。

综上所述，该问题本质上是一个涉及多因素影响、非线性关系、风险最小化以及复杂约束条件的非线性规划问题。其建模思路围绕着如何在满足生理医学要求的基础上，通过优化检测时机来实现风险最小化，体现了现代医疗决策中数学建模的重要作用。

问题3：男胎Y染色体浓度达标时间的最优时点选择

问题理解与模型建立

本问题要求我们基于男胎孕妇的BMI，结合身高、体重、年龄等因素，确定各BMI组的最佳NIPT检测时点，以最小化孕妇潜在风险。这是一个典型的非线性优化问题。

1. 决策变量设定

设第 $ i $ 组孕妇的最优检测时点为 $ t_i $，其中 $ i = 1,2,3,4,5 $ 对应BMI分组：$[20,28)$、$[28,32)$、$[32,36)$、$[36,40)$、$[40,+\infty )$。

2. 目标函数构建

我们的目标是最小化总风险，定义风险函数如下：

$$R(t_i)=\sum _{i=1}^5{w}_i\cdot r_i(t_i)$$

其中：

$w_i$ 表示第 $i$ 组孕妇在总人群中的权重；

$r_i(t_i)$ 是第 $i$ 组孕妇在时点 $t_i$ 下的潜在风险。

风险函数可以进一步表示为：

$$r_i(t_i)=\alpha \cdot P_{fail}(t_i)+\beta \cdot P_{late}(t_i)+\gamma \cdot \sigma (t_i)$$

其中：

$P_{fail}(t_i)$：检测失败概率；

$P_{late}(t_i)$：晚期发现概率；

$\sigma (t_i)$：Y染色体浓度达标比例的标准差（反映不确定性）；

$\alpha ,\beta ,\gamma$：权重系数，用于平衡不同风险因素的重要性。

3. 约束条件建模

(1) BMI分组约束

将孕妇按BMI分为五个区间：
$$\{\begin{array}{ll}[20,28)& \text{组1}\\ [28,32)& \text{组2}\\ [32,36)& \text{组3}\\ [36,40)& \text{组4}\\ [40,+\infty )& \text{组5}\end{array}$$

(2) Y染色体浓度达标约束

对于每组孕妇，在检测时点 $t_i$ 时，其Y染色体浓度应满足：
$$E[Y_{t_i}]\ge 4\%$$

其中 $E[Y_{t_i}]$ 是在时点 $t_i$ 时Y染色体浓度的期望值。

(3) 时间范围约束

检测时点必须在孕期10周至25周之间：
$$10\le t_i\le 25,i=1,2,3,4,5$$

(4) 检测失败率约束

考虑到检测误差和失败情况，引入一个检测成功率函数 $S(t_i)$，使得：
$$S(t_i)=1P_{fail}(t_i)$$

4. 非线性优化模型

最终的非线性规划模型如下：

$$\underset{t_1,t_2,t_3,t_4,t_5}{\min }R(t_1,t_2,t_3,t_4,t_5)$$

$$s.t.\{\begin{array}{ll}E[Y_{t_i}]\ge 4\%,& i=1,2,3,4,5\\ 10\le t_i\le 25,& i=1,2,3,4,5\\ {\sum }_{i=1}^5{w}_i=1& \\ w_i\ge 0,& i=1,2,3,4,5\end{array}$$

5. 具体建模步骤

步骤一：建立Y染色体浓度预测模型

假设Y染色体浓度随孕周变化遵循以下形式的函数关系：
$$Y(t;{\mu }_i,{\sigma }_i)=\frac{a_i}{1+e^{b_i(t{c}_i)}}+{ϵ}_i$$

其中：

$a_i$：最大浓度上限；

$b_i$：增长速率；

$c_i$：达到峰值的时间；

${ϵ}_i$：随机误差项。

通过回归分析拟合出各个BMI组的参数 $(a_i,b_i,c_i)$。

步骤二：计算检测失败概率

检测失败概率可由以下公式估算：
$$P_{fail}(t_i)=\exp (k_1\cdot t_i+k_2)$$

其中 $k_1,k_2$ 为经验参数，可通过历史数据拟合得到。

步骤三：计算晚期发现概率

晚期发现概率与检测时点相关，定义为：
$$P_{late}(t_i)=\{\begin{array}{ll}0,& t_i\le 12\\ \frac{t_{i}12}{15},& 12<t_i\le 27\\ 1,& t_i>27\end{array}$$

步骤四：考虑检测误差影响

设检测误差服从正态分布 $N(0,{\sigma }_e^2)$，则Y染色体浓度的实际观测值为：
$$Y_{obs}=Y(t_i)+{ϵ}_e,{ϵ}_e\sim N(0,{\sigma }_e^2)$$

6. 模型求解方法

使用非线性规划算法（如SQP、遗传算法GA等）进行求解，具体步骤如下：

1. 初始化：给定初始时点 $t_i^{(0)}$
2. 迭代优化：使用优化算法更新时点 $t_i$
3. 收敛判断：当目标函数变化小于预设阈值时停止迭代
4. 输出结果：最优时点 $t_i^{\ast }$ 及对应的风险评估

7. 检测误差敏感性分析

为了评估检测误差对结果的影响，我们进行如下分析：

(1) 误差对达标比例的影响

设检测误差为 $\delta$，则新的浓度估计为：
$$Y_{new}=Y_{true}+\delta$$

当 $\delta >0$ 时，可能导致部分原本合格的样本被误判为不合格；反之亦然。

(2) 误差对最佳时点的影响

引入误差项后，目标函数变为：
$$R^{\prime }(t_i)=R(t_i)+\Delta R(\delta )$$

其中 $\Delta R(\delta )$ 表示由于误差导致的风险增加量。

通过蒙特卡洛模拟方法，我们可以评估不同误差水平下最佳时点的变化情况。

8. 实际应用建议

根据上述模型计算结果，我们提出以下建议：

1. BMI分组策略：按照BMI值将孕妇分为五组，分别制定检测时点标准。
2. 个性化检测方案：根据不同BMI组的特点，调整检测时间点，确保Y染色体浓度达标。
3. 风险控制机制：设置动态风险预警系统，及时识别高风险孕妇并采取干预措施。
4. 误差管理策略：加强实验室质控，减少检测误差对结果的影响。

综上所述，通过构建非线性优化模型并结合实际数据，可以科学合理地确定各BMI组的最佳NIPT检测时点，从而有效降低孕妇潜在风险。

import numpy as np
from scipy.optimize import minimize
from scipy.stats import norm
import pandas as pd

# 模拟数据加载
# 假设data是一个包含BMI、孕周、Y染色体浓度等信息的DataFrame
# data = pd.read_csv('nipt_data.csv')

# 为了演示，我们构造一些模拟数据
np.random.seed(42)
n_samples = 1000
data = pd.DataFrame({
    'BMI': np.random.uniform(20, 50, n_samples),
    'age': np.random.randint(20, 40, n_samples),
    'height': np.random.normal(165, 8, n_samples),
    'weight': np.random.normal(65, 10, n_samples),
    'week': np.random.uniform(10, 25, n_samples),
    'Y_concentration': np.random.uniform(0, 10, n_samples)
})

# BMI分组
def assign_bmi_group(bmi):
    if 20 <= bmi < 28:
        return 1
    elif 28 <= bmi < 32:
        return 2
    elif 32 <= bmi < 36:
        return 3
    elif 36 <= bmi < 40:
        return 4
    else:
        return 5

data['bmi_group'] = data['BMI'].apply(assign_bmi_group)

# 定义各组的参数（模拟）
params = {
    1: {'a': 6.5, 'b': 0.3, 'c': 18},
    2: {'a': 7.0, 'b': 0.25, 'c': 19},
    3: {'a': 7.5, 'b': 0.2, 'c': 20},
    4: {'a': 8.0, 'b': 0.15, 'c': 21},
    5: {'a': 8.5, 'b': 0.1, 'c': 22}
}

# 检测失败概率模型
def detection_failure_probability(t, k1=0.1, k2=0.5):
    return np.exp(-k1 * t + k2)

# 晚期发现概率模型
def late_detection_probability(t):
    if t <= 12:
        return 0
    elif t <= 27:
        return (t - 12) / 15
    else:
        return 1

# 标准差模型（模拟）
def concentration_std(t):
    return 0.5 + 0.1 * t

# 风险函数
def risk_function(t, group, weights):
    # 获取该组的参数
    param = params[group]
    a, b, c = param['a'], param['b'], param['c']
    
    # 计算期望Y染色体浓度
    expected_y = a / (1 + np.exp(-b * (t - c)))
    
    # 约束条件：期望浓度必须大于等于4%
    if expected_y < 4:
        return float('inf')  # 不满足约束，返回无穷大
    
    # 计算各项风险指标
    fail_prob = detection_failure_probability(t)
    late_prob = late_detection_probability(t)
    std_dev = concentration_std(t)
    
    # 权重
    alpha, beta, gamma = 0.4, 0.4, 0.2
    
    # 总风险
    total_risk = alpha * fail_prob + beta * late_prob + gamma * std_dev
    
    return total_risk

# 优化函数
def optimize_nipt_timing(data):
    groups = [1, 2, 3, 4, 5]
    optimal_times = {}
    weights = {}
    
    # 计算每组的人数作为权重
    group_counts = data['bmi_group'].value_counts().sort_index()
    total_count = len(data)
    for group in groups:
        weights[group] = group_counts.get(group, 0) / total_count
    
    # 对每组单独优化
    for group in groups:
        def objective(t):
            return risk_function(t[0], group, weights)
        
        # 初始猜测
        initial_guess = [15]
        
        # 约束条件
        bounds = [(10, 25)]
        
        # 优化
        result = minimize(objective, initial_guess, bounds=bounds, method='L-BFGS-B')
        
        if result.success:
            optimal_times[group] = result.x[0]
        else:
            print(f"Group {group} optimization failed.")
            optimal_times[group] = 15  # 默认值
    
    return optimal_times, weights

# 执行优化
optimal_times, weights = optimize_nipt_timing(data)

# 输出结果
print("各BMI组最佳检测时点:")
for group, time in optimal_times.items():
    print(f"组{group}: {time:.2f}周")

print("\n各组权重:")
for group, weight in weights.items():
    print(f"组{group}: {weight:.2f}")

# 检测误差敏感性分析
def sensitivity_analysis(optimal_times, error_level=0.5):
    print(f"\n检测误差敏感性分析 (误差水平: ±{error_level})")
    for group, time in optimal_times.items():
        # 加入误差后的风险计算
        param = params[group]
        a, b, c = param['a'], param['b'], param['c']
        
        # 误差下的期望浓度
        expected_y_with_error = a / (1 + np.exp(-b * (time - c))) + np.random.normal(0, error_level)
        
        # 如果浓度低于4%，则可能影响检测结果
        if expected_y_with_error < 4:
            print(f"组{group}: 检测浓度可能不达标，建议调整检测时间")
        else:
            print(f"组{group}: 在误差范围内，检测浓度达标")

# 执行敏感性分析
sensitivity_analysis(optimal_times, error_level=0.5)

问题4

这是一个判别分析问题，核心在于通过已有的观测数据，构建分类模型以判断女胎是否存在染色体非整倍体异常。题干中明确指出需基于21号、18号和13号染色体的检测结果（AB列），并结合X染色体及其他相关因子（如Z值、GC含量、读段数、比例、BMI等）来进行综合判定。这种分类任务的本质是寻找一个最优的判别函数或规则，将样本划分到不同的类别中，属于典型的判别分析应用场景。

为什么这样判断？可以从以下几个特征点来说明：

（1）题干明确提出“判定女胎是否异常”的任务，这直接对应于分类问题。在统计学中，判别分析是处理此类问题的经典方法之一，尤其是当目标变量为类别型变量时，如正常/异常、健康/患病等。本题中的“异常”即表示胎儿是否存在染色体非整倍体问题，是一个二分类或多分类问题。

（2）题干强调使用多种指标进行综合判断，包括染色体Z值、GC含量、读段数、相关比例以及BMI等，这些构成了多维特征空间中的变量集合。这类多变量分类问题非常适合采用判别分析方法，尤其是线性判别分析（LDA）或二次判别分析（QDA），因为它们能够有效利用各个变量的信息来区分不同类别的样本。

（3）题目特别提到“女胎孕妇的21号、18号和13号染色体非整倍体（AB列）为判定结果”，说明已有标签数据可用于训练模型。也就是说，已知哪些样本属于“正常”或“异常”类别，这正是判别分析所需的基本信息，可以用来建立判别函数。

（4）题干还提及了“X染色体及上述染色体的Z值、GC含量、读段数及相关比例、BMI等因素”，这些变量可能具有不同的分布特性、相关性及重要程度，因此在建模过程中需考虑变量的选择、标准化、降维等预处理步骤。LDA/QDA均支持对变量进行加权处理，从而突出关键变量的影响，提升分类性能。

（5）题干中也提到了实际操作中的复杂情况，如测序失败、重复检测等，这些问题虽然增加了数据处理难度，但并不改变本题的核心建模思路——即通过已有数据建立有效的分类模型。即使面对不完整或噪声较多的数据，判别分析依然可以通过适当的方法（如缺失值填补、异常值剔除、正则化等）进行处理。

（6）从实际应用角度看，该问题属于医学诊断辅助决策领域，其最终目的是为医生提供科学依据以判断胎儿是否存在染色体异常。因此，模型不仅要有较高的准确率，还需要具备良好的解释性和稳定性，以便临床人员理解和使用。LDA/QDA作为传统且成熟的判别方法，在这方面表现良好，尤其适用于具有一定样本量的医学数据分析场景。

综上所述，本题要求根据大量生物医学数据，建立一个能够有效识别女胎是否存在染色体异常的判别模型，其数学本质是多变量分类问题，适用判别分析方法进行建模与求解。该问题类型应归类为“判别分析（LDA/QDA）”问题，其核心在于通过统计建模实现对胎儿染色体异常状态的自动识别与评估。

问题4：女胎异常的判定方法

1. 问题分析

本问题要求基于女胎孕妇的NIPT数据，综合考虑多个特征变量，建立判别模型来判断胎儿是否存在21号、18号和13号染色体非整倍体异常。这是一个典型的多分类判别分析问题，需要解决：

数据预处理：缺失值和异常值处理、特征标准化

模型构建：线性判别分析(LDA)和二次判别分析(QDA)

特征选择：主成分分析(PCA)或Fisher判别分析

模型验证：交叉验证、ROC曲线和AUC分析

异常判定：基于判别函数的阈值分类

2. 解决方案设计

2.1 数据预处理

首先对原始数据进行预处理：

# 特征变量定义
X = [X染色体Z值, X染色体GC含量, X染色体读段数, X染色体比例,
     21号染色体Z值, 21号染色体GC含量, 21号染色体读段数, 21号染色体比例,
     18号染色体Z值, 18号染色体GC含量, 18号染色体读段数, 18号染色体比例,
     13号染色体Z值, 13号染色体GC含量, 13号染色体读段数, 13号染色体比例,
     BMI]

# 缺失值处理
X_clean = impute_missing_values(X)

# 异常值处理
X_clean = remove_outliers(X_clean)

# 标准化处理
X_standardized = standardize_features(X_clean)

2.2 判别分析模型

2.2.1 线性判别分析(LDA)

LDA假设各类别的协方差矩阵相等，适用于类别间分布近似正态且协方差矩阵相似的情况。

LDA判别函数：
$${\delta }_k(x)=x^T{\Sigma }^1{\mu }_k\frac{1}{2}{\mu }_k^T{\Sigma }^1{\mu }_k+\ln ({\pi }_k)$$

其中：

${\mu }_k$：第k类的均值向量

$\Sigma$：所有类别的共同协方差矩阵

${\pi }_k$：第k类的先验概率

分类决策规则：
$$\hat{G}(x)=\arg \underset{k\in \mathcal{K}}{\max }{\delta }_k(x)$$

2.2.2 二次判别分析(QDA)

QDA允许各类别具有不同的协方差矩阵，更灵活但需要更多参数估计。

QDA判别函数：
$${\delta }_k(x)=\frac{1}{2}\log |{\Sigma }_k|\frac{1}{2}(x{\mu }_k{)}^T{\Sigma }_k^1(x{\mu }_k)+\ln ({\pi }_k)$$

其中${\Sigma }_k$是第k类的协方差矩阵。

2.3 特征选择与降维

使用主成分分析(PCA)进行特征降维：

$$Z=XW$$

其中$W$是特征向量构成的矩阵，$Z$是主成分得分向量。

2.4 模型训练与验证

2.4.1 交叉验证

采用k折交叉验证评估模型性能：

# k折交叉验证
for i in range(k):
    # 分割训练集和测试集
    X_train, X_test = split_data(X, i, k)
    y_train, y_test = split_labels(y, i, k)
    
    # 训练模型
    model.fit(X_train, y_train)
    
    # 预测并计算性能指标
    y_pred = model.predict(X_test)
    performance[i] = calculate_metrics(y_test, y_pred)

2.4.2 ROC曲线与AUC分析

对于多分类问题，计算每类的ROC曲线和AUC值：

$$AUC={\int }_0^{1}TPR(FPR)dFPR$$

其中TPR是真正例率，FPR是假正例率。

2.5 异常判定规则

2.5.1 基于判别函数阈值分类

对于每个样本$x$，计算各类别的判别函数值${\delta }_k(x)$，选择最大者作为预测类别：

$$\hat{G}(x)=\arg \underset{k=1}{\overset{K}{\max }}{\delta }_k(x)$$

2.5.2 结合多因素综合判断

考虑到实际应用中的不确定性，引入综合判断机制：

$$\text{判定结果}=\{\begin{array}{ll}\text{正常}& \text{if }\max ({\delta }_k)>{\theta }_{threshold}\\ \text{可疑}& \text{if }{\theta }_{low}<\max ({\delta }_k)<{\theta }_{threshold}\\ \text{异常}& \text{if }\max ({\delta }_k)<{\theta }_{low}\end{array}$$

3. 数学模型详细推导

3.1 LDA数学表达式

设总样本数为$n$，分为$K$类，第$k$类有$n_k$个样本，其观测值为$x_{ki}$，$i=1,2,...,n_k$。

类内散度矩阵：
$$S_W=\sum _{k=1}^K\sum _{i=1}^{n_k}(x_{ki}{\mu }_k)(x_{ki}{\mu }_k{)}^T$$

类间散度矩阵：
$$S_B=\sum _{k=1}^K{n}_k({\mu }_k\mu )({\mu }_k\mu {)}^T$$

其中$\mu =\frac{1}{n}{\sum }_{k=1}^K{n}_k{\mu }_k$是总体均值。

最优投影方向：
$$w=S_W^1({\mu }_1{\mu }_2)$$

3.2 QDA数学表达式

对于第$k$类，判别函数为：
$${\delta }_k(x)=\frac{1}{2}\log |{\Sigma }_k|\frac{1}{2}(x{\mu }_k{)}^T{\Sigma }_k^1(x{\mu }_k)+\ln ({\pi }_k)$$

3.3 PCA降维原理

目标是找到投影方向$w$使得投影后的方差最大化：

$$\underset{w}{\max }{w}^T{S}_{w}w\text{s.t.}{w}^{T}w=1$$

其中$S_w={\sum }_{i=1}^n(x_i\bar{x})(x_i\bar{x}{)}^T$是样本协方差矩阵。

4. 实施步骤总结

1. 数据预处理

处理缺失值和异常值

对所有特征进行标准化

2. 特征工程

构造特征组合

使用PCA提取主要成分

3. 模型构建

分别构建LDA和QDA模型

选择最优模型

4. 模型评估

交叉验证

ROC曲线和AUC分析

混淆矩阵分析

5. 结果输出

给出具体的判定阈值

提供性能指标报告

输出最终的判定方法

该方法能够有效识别女胎是否存在21号、18号和13号染色体异常，为临床诊断提供科学依据。

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis, QuadraticDiscriminantAnalysis
from sklearn.model_selection import cross_val_score, StratifiedKFold
from sklearn.metrics import classification_report, roc_curve, auc, confusion_matrix
from sklearn.decomposition import PCA
from sklearn.impute import SimpleImputer
import matplotlib.pyplot as plt
import seaborn as sns

# 读取数据（假设数据存储在CSV文件中）
# 数据包括：X染色体和各染色体的Z值、GC含量、读段数、比例、BMI等特征
# 以及标签：21号、18号、13号染色体非整倍体状态（正常/异常）

# 示例数据加载
# df = pd.read_csv('nipt_data.csv')

# 为演示目的，创建模拟数据结构
np.random.seed(42)
n_samples = 1000

# 模拟特征数据
data = {
    'X_Z': np.random.normal(0, 1, n_samples),
    'X_GC': np.random.uniform(0.3, 0.7, n_samples),
    'X_Reads': np.random.poisson(1000, n_samples),
    'X_Ratio': np.random.uniform(0.4, 0.6, n_samples),
    '21_Z': np.random.normal(0, 1, n_samples),
    '21_GC': np.random.uniform(0.3, 0.7, n_samples),
    '21_Reads': np.random.poisson(1000, n_samples),
    '21_Ratio': np.random.uniform(0.4, 0.6, n_samples),
    '18_Z': np.random.normal(0, 1, n_samples),
    '18_GC': np.random.uniform(0.3, 0.7, n_samples),
    '18_Reads': np.random.poisson(1000, n_samples),
    '18_Ratio': np.random.uniform(0.4, 0.6, n_samples),
    '13_Z': np.random.normal(0, 1, n_samples),
    '13_GC': np.random.uniform(0.3, 0.7, n_samples),
    '13_Reads': np.random.poisson(1000, n_samples),
    '13_Ratio': np.random.uniform(0.4, 0.6, n_samples),
    'BMI': np.random.normal(28, 5, n_samples),
    'Label': np.random.choice(['Normal', 'Abnormal'], n_samples)
}

df = pd.DataFrame(data)

# 特征选择
feature_columns = [
    'X_Z', 'X_GC', 'X_Reads', 'X_Ratio',
    '21_Z', '21_GC', '21_Reads', '21_Ratio',
    '18_Z', '18_GC', '18_Reads', '18_Ratio',
    '13_Z', '13_GC', '13_Reads', '13_Ratio',
    'BMI'
]

X = df[feature_columns]
y = df['Label']

# 缺失值处理
imputer = SimpleImputer(strategy='mean')
X_imputed = imputer.fit_transform(X)

# 异常值处理（使用IQR方法）
def remove_outliers(df, columns):
    for col in columns:
        Q1 = df[col].quantile(0.25)
        Q3 = df[col].quantile(0.75)
        IQR = Q3 - Q1
        lower_bound = Q1 - 1.5 * IQR
        upper_bound = Q3 + 1.5 * IQR
        df[col] = df[col].clip(lower=lower_bound, upper=upper_bound)
    return df

X_cleaned = remove_outliers(pd.DataFrame(X_imputed, columns=feature_columns), feature_columns)

# 标准化处理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_cleaned)

# 将标签转换为数值型
y_numeric = pd.get_dummies(y, drop_first=True).values.ravel()

# 使用PCA进行降维
pca = PCA(n_components=0.95)  # 保留95%的方差
X_pca = pca.fit_transform(X_scaled)

print("PCA explained variance ratio:", pca.explained_variance_ratio_)
print("Number of components used:", pca.n_components_)

# 分割训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
    X_pca, y_numeric, test_size=0.2, random_state=42, stratify=y_numeric
)

# 构建LDA模型
lda_model = LinearDiscriminantAnalysis()
lda_model.fit(X_train, y_train)

# 构建QDA模型
qda_model = QuadraticDiscriminantAnalysis()
qda_model.fit(X_train, y_train)

# 交叉验证评估
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
lda_scores = cross_val_score(lda_model, X_train, y_train, cv=cv, scoring='accuracy')
qda_scores = cross_val_score(qda_model, X_train, y_train, cv=cv, scoring='accuracy')

print("LDA Cross-validation scores:", lda_scores)
print("QDA Cross-validation scores:", qda_scores)

# 预测
y_pred_lda = lda_model.predict(X_test)
y_pred_qda = qda_model.predict(X_test)

# 输出分类报告
print("\nLDA Classification Report:")
print(classification_report(y_test, y_pred_lda))

print("\nQDA Classification Report:")
print(classification_report(y_test, y_pred_qda))

# 混淆矩阵可视化
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
cm_lda = confusion_matrix(y_test, y_pred_lda)
sns.heatmap(cm_lda, annot=True, fmt='d', cmap='Blues')
plt.title('LDA Confusion Matrix')
plt.ylabel('True Label')
plt.xlabel('Predicted Label')

plt.subplot(1, 2, 2)
cm_qda = confusion_matrix(y_test, y_pred_qda)
sns.heatmap(cm_qda, annot=True, fmt='d', cmap='Blues')
plt.title('QDA Confusion Matrix')
plt.ylabel('True Label')
plt.xlabel('Predicted Label')

plt.tight_layout()
plt.show()

# ROC曲线和AUC分析（二分类情况）
from sklearn.metrics import roc_auc_score

y_proba_lda = lda_model.predict_proba(X_test)[:, 1]
y_proba_qda = qda_model.predict_proba(X_test)[:, 1]

fpr_lda, tpr_lda, _ = roc_curve(y_test, y_proba_lda)
auc_lda = auc(fpr_lda, tpr_lda)

fpr_qda, tpr_qda, _ = roc_curve(y_test, y_proba_qda)
auc_qda = auc(fpr_qda, tpr_qda)

plt.figure(figsize=(8, 6))
plt.plot(fpr_lda, tpr_lda, label=f'LDA AUC = {auc_lda:.2f}')
plt.plot(fpr_qda, tpr_qda, label=f'QDA AUC = {auc_qda:.2f}')
plt.plot([0, 1], [0, 1], 'k--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curves Comparison')
plt.legend(loc='lower right')
plt.grid(True)
plt.show()

# 最终异常判定规则
def predict_abnormality(model, sample_data, threshold=0.5):
    prob = model.predict_proba(sample_data)[0][1]
    if prob >= threshold:
        return "Abnormal"
    else:
        return "Normal"

# 示例预测
sample = X_pca[0:1]
print("\nSample Prediction using LDA:", predict_abnormality(lda_model, sample))
print("Sample Prediction using QDA:", predict_abnormality(qda_model, sample))

更多内容具体可以看看我的下方名片！里面包含有国赛一手资料与分析！
另外在赛中，我们也会陪大家一起解析国赛的一些方向！
关注 CS数模 团队，数模不迷路！