1.1鸽巢原理的简单形式

如果把n+1件物品放进n个抽屉，必定存在至少一个抽屉里有超过两件物品。
证明：使用反证法
假设n个抽屉至多有1件物品，那么至多有n件物品，与有n+1件物品的条件矛盾，故鸽巢原理成立。

例题

例1. 证明任意选取的 n + 1个整数中，必存在两个数，它们的差为n的倍数。
可以使用鸽巢原理（抽屉原理），具体步骤如下：

1. 余数分类：
   每个整数除以 $n$ 的余数只有$0,1,2,\dots ,n-1$ 这 $n$ 种可能。将整数按余数分为 $n$) 类（即 $n$ 个“抽屉”）。

2. 应用鸽巢原理：
   若选取 $n+1$ 个整数（即$n+1$个“物品”），根据鸽巢原理，至少有两个数属于同一余数类，即这两个数的余数相同。

3. 推导差值性质：
   设这两个数为 $a=n\cdot q_1+r$和$b=n\cdot q_2+r$，其中$r$ 是相同的余数。它们的差为：
   $$a-b=n\cdot (q_1-q_2),$$
   显然$a-b$ 是$n$ 的倍数。

结论：
因此，任意选取的$n+1$ 个整数中，必存在两个数，它们的差为$n$ 的倍数。

---

1.2鸽巢原理的加强形式

若把$q_1+q_2+\dots +q_n-n+1$个物品放进n个抽屉，则第$i$个抽屉里至少有$q_i$个物品，$i\in [1,n]$。
证明：同样是反证法
假设第$i$个抽屉里最多$q_i-1$件物品，则n个抽屉最多有$q_1+q_2+\dots +q_n-n$件物品，与题设矛盾，故原定理成立。

这个定理令$q_1=q_2=\cdots =q_n=r$有几条推论：

推论 1.2.1

若将 $n(r-1)+1$ 个物品放入 $n$ 个盒子中，则至少有一个盒子中有 $r$ 个物品。

---

推论 1.2.2

设 $m_1,m_2,\cdots ,m_n$ 是$n$ 个整数，且满足：
$$\frac{m_1+m_2+\cdots +m_n}{n}>r-1,$$
则 $m_1,m_2,\cdots ,m_n$ 中至少有一个数不小于$r$。

---

推论 1.2.3

若将 $m$ 个物品放入 $n$ 个盒子中，则至少有一个盒子中有不少于
$$\lceil \frac{m}{n}\rceil$$
个物品。其中，$\lceil \frac{m}{n}\rceil$ 是不小于 $\frac{m}{n}$ 的最小整数，即向下取整。

1.3Ramsey问题与Ramsey数

1.3.1Ramsey问题

内容：任何6人的聚会，总有3人互相认识或3人互相不认识
证明：通过图论和鸽巢原理：

---

1. 问题转化为图论模型
将6人视为图的6个顶点，边表示两人之间的关系：

• 若两人认识，边染为红色；
• 若两人不认识，边染为蓝色。
  我们需要证明图中必然存在一个红色三角形（3人互相认识）或一个蓝色三角形（3人互相不认识）。

---

2. 选取任意一人A，分析其与其他5人的关系
根据鸽巢原理，A与其他5人的边中，至少存在$\lceil \frac{5}{2}\rceil =3$条边颜色相同，则有以下两种情形：

• 情形1：A至少与3人认识（至少有3条红边）；
• 情形2：A至少与3人不认识（至少有3条蓝边）。

---

3. 对两种情形分别讨论

情形1：A至少认识3人（设为B、C、D）

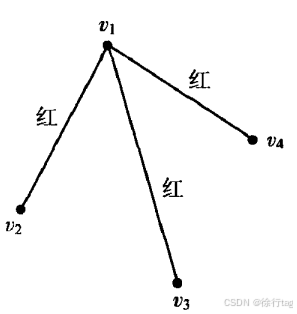
BCD之间三条边用两种颜色连接至少有$\lceil \frac{3}{2}\rceil =2$条边颜色相同

• 若B、C、D中有任意两人互相认识（存在红边），则这两人与A构成一个红色三角形。
• 若B、C、D之间均不认识（所有边为蓝色），则B、C、D构成一个蓝色三角形。

情形2：A至少不认识3人（设为B、C、D）
同理

• 若B、C、D中有任意两人互不认识（存在蓝边），则这两人与A构成一个蓝色三角形。
• 若B、C、D之间均认识（所有边为红色），则B、C、D构成一个红色三角形。

---

4. 结论
无论哪种情形，必然存在一个红色三角形或蓝色三角形，即存在3人互相认识或互相不认识。

---

1.3.2Ramsey数

定义：
完全图：若n个顶点之间，任意两个点之间有一条边，则这个图为完全图$K_n$。
前面的Ramsey问题即：在$K_6$中至少有一个红色或蓝色$K_3$。
拓展可得Ramsey数的定义：
对于任意正整数$m$ 和 $n$，Ramsey数 $R(m,n)=N$表示满足以下条件的最小正整数$N$：
无论将$N$ 个顶点的完全图的边如何染成红色或蓝色，图中必然存在一个由 $m$个顶点组成的红色完全子图，或者一个由$n$ 个顶点组成的蓝色完全子图。

---

经典例子

• $R(3,3)=6$：在任意6人的聚会中，总有3人互相认识（红色三角形）或3人互相不认识（蓝色三角形）。这是Ramsey理论中最著名的结论。

---

数学表述
r(m,n)=min⁡{N∈N∗∣任意 N 顶点的红蓝边完全图必含红 Km 或蓝 Kn} r(m, n) = \min \left\{ N \in \mathbb{N}^* \mid \text{任意 } N \text{ 顶点的红蓝边完全图必含红 } K_m \text{ 或蓝 } K_n \right\} r(m,n)=min{N∈N∗∣任意 N 顶点的红蓝边完全图必含红 Km​ 或蓝 Kn​}

---

表中是已知的Ramsey数：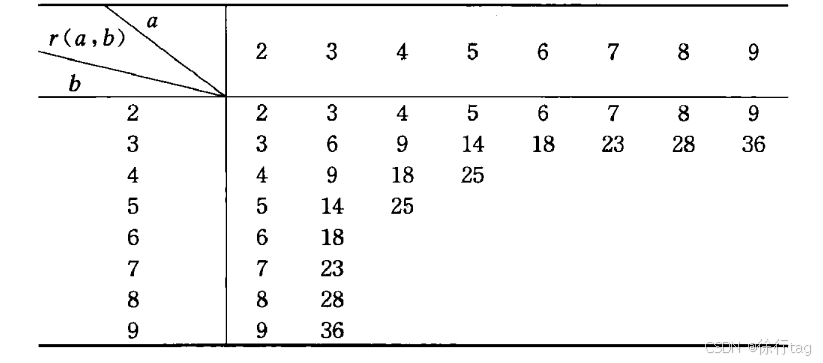

1.3.3相关定理

1. 对于任意$a\ge 3,b\ge 3$有$r(a,b)\le r(a-1,b)+r(a,b-1)$
2. 对于每对正整数$p,q$，Ramsey 数 $r(p,q)$ 存在且满足$r(p,q)\le \left(\genfrac{}{}{0ex}{}{p+q-2}{p-1}\right)$
   证明：通过数学归纳法：

---

1. 基础情形
当 $p=1$ 或 $q=1$ 时，Ramsey 数为：
$$r(1,q)=1\text{和}r(p,1)=1.$$
此时，组合数上界为：
$$\left(\genfrac{}{}{0ex}{}{1+q-2}{0}\right)=1\text{和}\left(\genfrac{}{}{0ex}{}{p+1-2}{p-1}\right)=1,$$
显然成立。

---

2. 归纳假设
假设对所有满足 $p^{\prime }+q^{\prime }<p+q$ 的正整数对$(p^{\prime },q^{\prime })$，命题成立，即：
$$r(p^{\prime },q^{\prime })\le \left(\genfrac{}{}{0ex}{}{p^{\prime }+q^{\prime }-2}{p^{\prime }-1}\right).$$

---

3. 归纳步骤
考虑 $r(p,q)$。根据 Ramsey 数的递归不等式：
$$r(p,q)\le r(p-1,q)+r(p,q-1).$$
由归纳假设，右侧满足：
$$r(p-1,q)\le \left(\genfrac{}{}{0ex}{}{(p-1)+q-2}{(p-1)-1}\right)=\left(\genfrac{}{}{0ex}{}{p+q-3}{p-2}\right),$$
$$r(p,q-1)\le \left(\genfrac{}{}{0ex}{}{p+(q-1)-2}{p-1}\right)=\left(\genfrac{}{}{0ex}{}{p+q-3}{p-1}\right).$$
因此，
$$r(p,q)\le \left(\genfrac{}{}{0ex}{}{p+q-3}{p-2}\right)+\left(\genfrac{}{}{0ex}{}{p+q-3}{p-1}\right).$$
根据组合数的加法公式$\left(\genfrac{}{}{0ex}{}{n-1}{k-1}\right)+\left(\genfrac{}{}{0ex}{}{n-1}{k}\right)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)$，得：
$$r(p,q)\le \left(\genfrac{}{}{0ex}{}{p+q-2}{p-1}\right).$$

---

4. 存在性
通过归纳法可知，对所有$p,q$，$r(p,q)$ 的上界为有限数，因此$r(p,q)$ 必然存在。

---

1.4 Ramsey数扩展形式

把原来的Ramsey数的定义扩展到n种颜色，就得到了Ramsey数扩展形式的定义。记为：
$$r(a_1,a_2,\dots ,a_n)=N$$

Ramsey定理：

$N(q_1,q_2,\dots ,q_n;t)$表示满足定理条件的整数。其中下标n表示用n种颜色，t表示把t个物品绑定成一个整体进行划分。