---

引言

我自认空间想象能力较差，所以当初学这个很吃力。希望现在再接触，能好点。

---

一、空间解析几何的理论

1.1 基本概念

1.向量 —— 既有大小，又有方向的量称为向量，常用从起点指向终点的带箭头的有向线段 $\overrightarrow{AB}$ 表示，或用带箭头的小写字母 $\overrightarrow{a}$ 。

向量的大小或长度称为向量的模，向量 $\overrightarrow{a}$ 的模记作 $|\overrightarrow{a}|$ 。特别地，模为 1 的向量称为单位向量，模为 0 的向量称为零向量，记作 ${\overrightarrow{a}}^0$ 。大小相等且方向相同的向量相等。

2.向量的坐标 —— 设 $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ 分别表示 $x,y,z$ 轴正向的单位向量，设向量 $\overrightarrow{a}$ 在三个坐标轴上的投影分别为 $a,b,c$ ，由向量的分解得 a → = a i → + b j → + c k → = { a , b , c } \overrightarrow{a}=a\overrightarrow{i}+b\overrightarrow{j}+c\overrightarrow{k}=\{a,b,c\} a =ai +bj ​+ck ={a,b,c} ，称 { a , b , c } \{a,b,c\} {a,b,c} 为向量 $\overrightarrow{a}$ 的坐标。

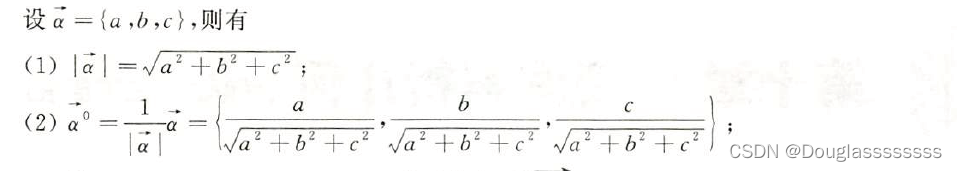
3.向量的方向角和方向余弦 —— 设 a → = { a , b , c } \overrightarrow{a}=\{a,b,c\} a ={a,b,c} 为非零向量，则 $\overrightarrow{a}$ 与 $x,y,z$ 轴正向的夹角，称为此向量的方向角，分别记为 $\alpha ,\beta ,\gamma$ ，称 $\cos \alpha ,\cos \beta ,\cos \gamma$ 为 $\overrightarrow{a}$ 的方向余弦。则 $$\cos \alpha =\frac{a}{\sqrt{a^2+b^2+c^2}},\cos \beta =\frac{b}{\sqrt{a^2+b^2+c^2}},\cos \alpha =\frac{c}{\sqrt{a^2+b^2+c^2}}$$ 显然，有 a → 0 = { cos ⁡ α , cos ⁡ β , cos ⁡ γ } \overrightarrow{a}^0=\{\cos\alpha,\cos\beta,\cos\gamma\} a 0={cosα,cosβ,cosγ} ，$\cos {\alpha }^2+\cos {\beta }^2+\cos {\gamma }^2=1$ 。

4.向量在一个轴（向量）上的投影 —— 设 $u$ 为一个数轴，$\overrightarrow{a}$ 为一个向量，过向量的起点 A 和终点 B 作 $u$ 轴的垂直面交 $u$ 轴于点 $A_1,B_1$ ，其在 $u$ 轴上的坐标分别为 $x_1,x_2$ ，称 $x_2-x_1$ 为向量 $\overrightarrow{a}$ 在 $u$ 轴上的投影，记为 $Pr{j}_u\overrightarrow{a}=x_2-x_1$ ，且 $Pr{j}_u\overrightarrow{a}=|\overrightarrow{a}|\cos (u,\overrightarrow{a})$ 。

1.2 向量的运算

（一）几何描述

加减法，遵循三角形法则。

（二）代数描述

主要说一下叉乘（向量积）的代数形式（注意，求 $y$ 的系数时，要像行列式里面求第一行第二列的代数余子式一样，加上一个负号）：

下面是一些运算的性质：

补充：数量积还满足分配律 $\overrightarrow{a}\cdot (\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}\overrightarrow{b}+\overrightarrow{a}\overrightarrow{c}$ 和与常数的结合律 $(\lambda \overrightarrow{a})\cdot \overrightarrow{b}=\lambda (\overrightarrow{a}\cdot \overrightarrow{b})$ 。向量积还具有以下性质。

1. $\overrightarrow{a}\times \overrightarrow{a}=\overrightarrow{0}$ ；
2. 分配律：$(\overrightarrow{a}+\overrightarrow{b})\times \overrightarrow{c}=\overrightarrow{a}\times \overrightarrow{c}+\overrightarrow{b}\times \overrightarrow{c}$ ；
3. 与常数的结合律：$(\lambda \overrightarrow{a})\times \overrightarrow{b}=\lambda (\overrightarrow{a}\times \overrightarrow{b})$ 。

（三）混合积

已知三个向量 $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ ，作 $(\overrightarrow{a}\times \overrightarrow{b})\cdot \overrightarrow{c}$ ，称为三向量的混合积，记为 $[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]$ 。设 a → = { a x , a y , a z } , b → = { b x , b y , b z } , c → = { c x , c y , c z } \overrightarrow{a}=\{a_x,a_y,a_z\},\overrightarrow{b}=\{b_x,b_y,b_z\},\overrightarrow{c}=\{c_x,c_y,c_z\} a ={ax​,ay​,az​},b ={bx​,by​,bz​},c ={cx​,cy​,cz​} ，有 $$[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]=\left|\begin{array}{ccc}{a}_x& a_y& a_z\\ b_x& b_y& b_z\\ c_x& c_y& c_z\end{array}\right|$$ 向量的混合积具有轮换对称性，即有 $[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]=[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]=[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]$ 。

混合积的绝对值表示以向量 $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ 为棱的平行六面体的体积。如果 $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ 组成右手系，那么混合积的值为正。

三向量 $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ 共面的充要条件是它们的混合积 $[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}]=0$ 。

---

写在最后

有关向量的基本概念和性质基本就这些，下一篇我们就来看看向量有哪些应用。