论文发表于人工智能顶会ICLR（原文链接）。基于定位和修改的模型编辑方法（针对ROME和MEMIT等）会破坏LLM中最初保存的知识，特别是在顺序编辑场景。为此，本文提出AlphaEdit：

  1、在将保留知识应用于参数之前，将扰动投影到保留知识的零空间上。

  2、从理论上证明，这种预测确保了在查询保留的知识时，编辑后的LLM的输出保持不变，从而减轻中断问题。

  3、对各种LLM（包括LLaMA3、GPT2XL和GPT-J）的广泛实验表明，AlphaEdit只需一行额外的投影代码，即可将大多数定位编辑方法的性能平均提高36.4%。

  阅读本文请同时参考原始论文图表。

1  AlphaEdit#

1.1  零空间#

  基于前面ROME/MEMIT的工作，对于LLM中的MLP矩阵W�，可被表示为关于已有知识(K0,V0)(�0,�0)的优化结果：

W=argmin~W∥∥~WK0−V0∥∥2�=arg⁡min�~‖�~�0−�0‖2

  其中矩阵K0∈Rd0×n,V0∈Rd0×n�0∈��0×�,�0∈��0×�，n�表示已有知识数量。对于新增知识(K1,V1)(�1,�1)，MEMIT的做法为优化扰动ΔΔ来更新W�：

Δ=argmin~Δ(∥∥(W+~Δ)K1−V1∥∥2+∥∥(W+~Δ)K0−V0∥∥2)Δ=arg⁡minΔ~(‖(�+Δ~)�1−�1‖2+‖(�+Δ~)�0−�0‖2)

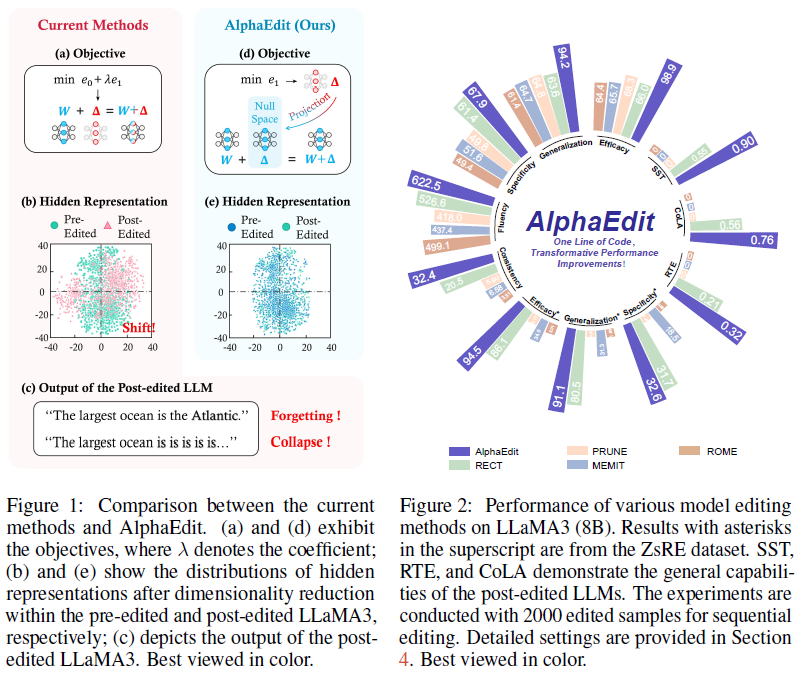
  上式为二次优化，可通过求导直接获得闭式解。然而，耦合的优化不可避免会是扰动量对原始知识产生影响，从而在终身编辑场景中鲁棒性不强。文中通过将中间token表示映射到二维空间的分布偏移来表明这一观点：如图1be所示，MEMIT在编辑后token表示的分布产生了较大偏移，而AlphaEdit则没有。

  因此，AlphaEdit期望找到K0�0的零空间，把ΔΔ映射到其上，从而权重更新将对这些知识不产生影响。矩阵B�在矩阵A�的零空间内，当且仅当BA=0��=0。也就是说，期望找到ΔΔ有：

(W+Δ)K0=WK0=V0(�+Δ)�0=��0=�0

  那么如何将ΔΔ映射到K0�0的零空间呢？

1.2  SVD分解获取零空间映射#

  考虑对称方阵K0KT0∈Rd0×d0�0�0�∈��0×�0，对其进行奇异值分解（SVD），得到：

{U,Λ,UT}=SVD(K0KT0){�,Λ,��}=SVD(�0�0�)

  其中U�为正交矩阵（UUT=I���=�），ΛΛ对角矩阵，主对角线为奇异值。将奇异值在主对角线降序排序：

Λ=[Λ100Λ2]Λ=[Λ100Λ2]

  取其中为零的部分Λ2Λ2（假设Λ2Λ2都很小几乎为0，文中取小于0.01的值）在U�中对应的特征向量矩阵^U∈Rd0×m�^∈��0×�。则P=^U^UT�=�^�^�为将任意矩阵映射到K0KT0�0�0�零空间的矩阵。这是由于，对于任意矩阵ΔΔ，有：

ΔPK0KT0=Δ^U^UTK0KT0=Δ^U^UTUΛUTΔ��0�0�=Δ�^�^��0�0�=Δ�^�^��Λ��

  由于其中^UTUΛ=0�^��Λ=0，上式为零。P�为K0KT0�0�0�的零空间映射矩阵，同时也K0�0的零空间映射矩阵，这是由于：

PK0KT0=0⇒PK0KTPT=0⇒PK0(KP)T=0⇒PK0=0��0�0�=0⇒��0����=0⇒��0(��)�=0⇒��0=0

1.3  AlphaEdit优化#

  基于ROME/EMMIT工作，K0KT0�0�0�可通过计算10万条数据获得，即可进一步获得映射矩阵P�。有了P�，优化就无需再考虑原有知识K0�0，则AlphaEdit将优化式改为：

Δ=argmin~Δ(∥∥(W+~ΔP)K1−V1∥∥2+∥∥~ΔP∥∥2+∥∥~ΔPKp∥∥2)Δ=arg⁡minΔ~(‖(�+Δ~�)�1−�1‖2+‖Δ~�‖2+‖Δ~���‖2)

  其中第二项控制ΔΔ的范数，避免数值过大，第三项额外考虑终身编辑场景中已编辑的知识(Kp,Vp)(��,��)。原始MEMIT没有考虑第三项。求导得到方程：

(ΔPK1−R)KT1P+ΔP+ΔPKpKTpP=0(Δ��1−�)�1��+Δ�+Δ�������=0

  其中R=V1−WK1�=�1−��1表示新值V1�1与原始矩阵在新键下的残差。可得AlphaEdit的矩阵变化量ΔAlphaEditΔAlphaEdit为：

ΔAlphaEdit=ΔP=RKT1P(KpKTpP+K1KT1P+I)−1ΔAlphaEdit=Δ�=��1��(������+�1�1��+�)−1

  MEMIT的原始闭式解如下所示（额外考虑了已编辑知识），文中表明，仅仅这里改动一行代码，产生较好的编辑性能。

ΔMEMIT=RKT1(KpKTpP+K1KT1+K0KT0)−1ΔMEMIT=��1�(������+�1�1�+�0�0�)−1

2  实验#

  表1：2000条知识的编辑实验，AlphaEdit的编辑批量为100，编辑20次。

  图5：token表示分布偏移对比。

  其它图表：一些对比和增强效果。