一、决策树 - 分类

1、决策树基本概念

决策树是一种类似流程图的结构，通过一系列的问题对数据进行分类或预测。就像玩"20个问题"游戏，通过是/否问题逐步缩小可能性。

组成部分：

1. 决策节点：通过条件判断而进行分支选择的节点。提出问题的地方（如"年龄>30吗？"）

2. 分支：问题的可能答案

3. 叶节点：没有子节点的节点，表示最终的决策结果。

决策树的深度 所有节点的最大层次数。

决策树具有一定的层次结构，根节点的层次数定为0，从下面开始每一层子节点层次数增加

决策树优点：

可视化 - 可解释能力-对算力要求低

决策树缺点：

容易产生过拟合，所以不要把深度调整太大了。

简单示例：判断动物

假设我们有如下数据：

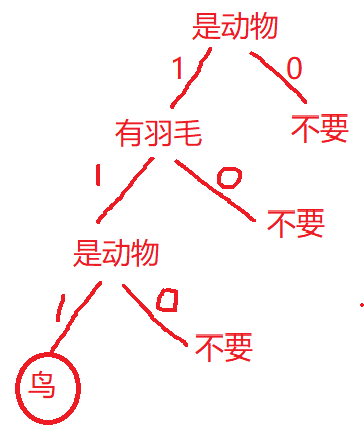
1. 	是动物	会飞	有羽毛
   1麻雀	1	1	1
   2蝙蝠	1	1	0
   3飞机	0	1	0
   4熊猫	1	0	0

   是否为动物

   	是动物	会飞	有羽毛
   1麻雀	1	1	1
   2蝙蝠	1	1	0
   4熊猫	1	0	0

   是否会飞

   	是动物	会飞	有羽毛
   1麻雀	1	1	1
   2蝙蝠	1	1	0

   是否有羽毛

   	是动物	会飞	有羽毛
   1麻雀	1	1	1

2、决策树的构建方法

1、基于信息增益决策树的建立

核心思想：信息增益决策树倾向于选择取值较多的属性，在有些情况下这类属性可能不会提供太多有价值的信息，算法只能对描述属性为离散型属性的数据集构造决策树。

1. 信息熵

信息熵是衡量数据集不确定性（混乱程度）的指标，熵越大，数据集越混乱；熵越小，数据集越纯净。

数据集纯净作用：

• 提高分类准确性：纯净的数据子集可以直接作为叶节点，无需进一步划分

• 优化决策树结构：决策树的构建目标是通过分裂使子节点尽可能纯净

• 增强模型可解释性：纯净的叶节点对应明确的分类规则

• 减少计算开销：如果数据已经纯净，则无需继续分裂，节省计算资源。

信息熵公式

假设数据集 DD 有 K 个类别，第 k类样本所占比例为 pk，则信息熵定义为：

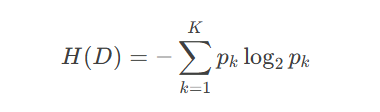
信息熵计算示例

假设有一个数据集 DD（是否贷款），其中：

• "是" 贷款的有 4 个样本

• "否" 贷款的有 2 个样本

计算信息熵：

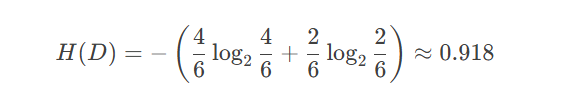
2.信息增益（减少不确定性）

信息增益是一个统计量，用来描述一个属性区分数据样本的能力。信息增益越大，那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量。

信息增益公式：

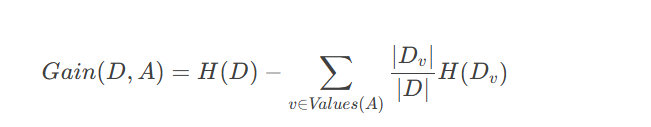
• H(D)：原始数据集的信息熵

• A：某个特征（如"职业"、"年龄"等）

• Values(A)：特征 A的所有可能取值

• Dv：特征 AA 取值为 v的子数据集

• ∣Dv|/|D|：子数据集 Dv 占整个数据集 D的比例

信息增益计算示例

继续使用贷款数据集：

样本	职业	年龄	收入	学历	是否贷款
1	工人	36	5500	高中	否
2	工人	42	2800	初中	是
3	白领	45	3300	小学	是
4	白领	25	10000	本科	是
5	白领	32	8000	硕士	否
6	白领	28	13000	博士	是

(1) 计算"职业"的信息增益

• "职业"有两个取值：工人（2个样本）、白领（4个样本）

• 工人子集 D工人*D*工人

  • "是"贷款：1 个

  • "否"贷款：1 个

  • 熵：

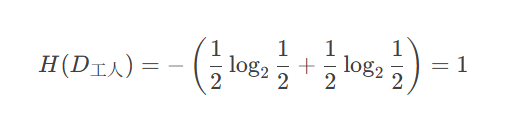
• 白领子集 D白领*D*白领

  • "是"贷款：3 个

  • "否"贷款：1 个

  • 熵：

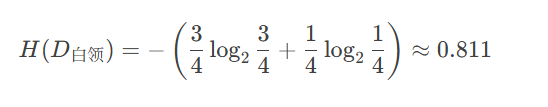
• 信息增益

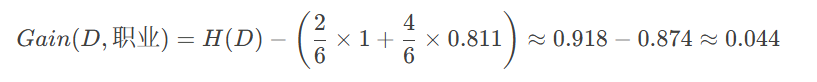
(2) 计算"收入"的信息增益（以10000为界）

• 收入 ≥ 10000（2个样本）

  • "是"贷款：2 个

  • "否"贷款：0 个

  • 熵：

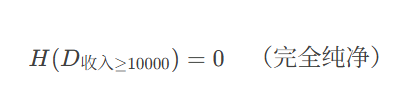
• 收入 < 10000（4个样本）

  • "是"贷款：2 个

  • "否"贷款：2 个

  • 熵：

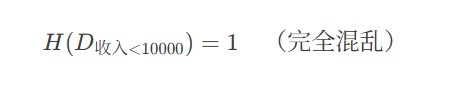
• 信息增益

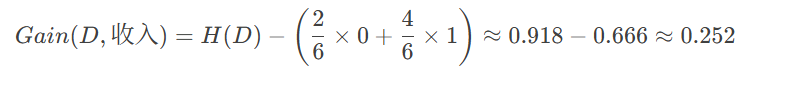
(3) 比较信息增益

• 职业：0.044

• 收入：0.252

• 学历（计算略）：0.252

• 年龄（计算略）：0.042

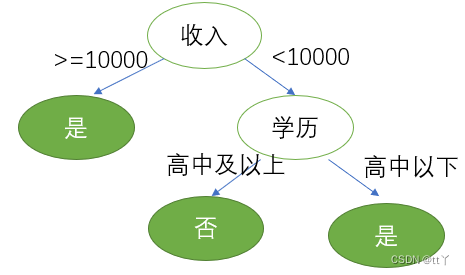
结论："收入"和"学历"的信息增益最大（0.252），因此优先选择它们作为决策树的第一个节点。

计算步骤：

1. 计算当前数据集的信息熵（混乱程度）

2. 计算每个特征的信息增益

3. 选择信息增益最大的特征作为决策节点

4. 对每个分支重复上述过程

2、基于基尼指数决策树的建立(了解)

基尼指数（Gini Index）是决策树算法中用于评估数据集纯度的一种度量，基尼指数衡量的是数据集的不纯度，或者说分类的不确定性。在构建决策树时，基尼指数被用来决定如何对数据集进行最优划分，以减少不纯度。

1. 核心目标：分得越纯越好

决策树的任务就像把一堆混乱的弹珠（数据）按颜色（类别）分开。

• 基尼指数就是衡量“筐子里弹珠颜色有多乱”的指标。

  • 如果筐里全是红色弹珠（同一类），基尼指数=0（最纯）。

  • 如果红蓝弹珠各一半，基尼指数=0.5（最乱）。

决策树的目标：每次分裂都选一个最有效的筛子（特征），让分出来的子筐颜色尽量一致！

---

2. 怎么选“筛子”？

假设你要用“工资高低”或“公司大小”来预测“工作是否满意”：

1. 先试“工资”筛子：

   • 高工资的筐：3个人全满意 → 基尼指数=0（纯！）。

   • 低工资的筐：5个人中3人不满意 → 基尼指数=0.48（有点乱）。

   • 整体不纯度 = (3/8)×0 + (5/8)×0.48 ≈ 0.3。

2. 再试“公司大小”筛子：

   • 小公司的筐：2个人全满意 → 基尼指数=0。

   • 非小公司的筐：6个人中3人满意 → 基尼指数=0.5（更乱）。

   • 整体不纯度 = (2/8)×0 + (6/8)×0.5 ≈ 0.375。

结论：用“工资”筛子分出来的筐更纯（0.3 < 0.375），所以优先选它！

---

3. 递归分筐，直到没法再分

• 第一层筛子（工资）：

  • 高工资 → 直接贴标签“满意”（纯筐，结束）。

  • 低工资 → 继续分。

• 第二层筛子（公司大小）：

  • 小公司 → 全满意（纯筐，结束）。

  • 非小公司 → 全不满意（纯筐，结束）。

3、sklearn API

1. 核心类：DecisionTreeClassifier（分类决策树）

​

from sklearn.tree import DecisionTreeClassifier

参数	说明	可选值	默认值
criterion	分裂标准	"gini"（基尼指数）或 "entropy"（信息增益）	"gini"
max_depth	树的最大深度	整数（如3）或 None（不限制）	None
min_samples_split	节点分裂的最小样本数	整数或浮点数（比例）	2
min_samples_leaf	叶子节点的最小样本数	整数或浮点数（比例）	1
random_state	随机种子（控制随机性）	整数	None

示例：

# 使用基尼指数，限制树深度为3
model = DecisionTreeClassifier(criterion="gini", max_depth=3, random_state=42)
model.fit(X_train, y_train)

2. 可视化工具：export_graphviz（生成决策树图）

from sklearn.tree import export_graphviz

参数	说明	示例
estimator	训练好的决策树模型	model
out_file	输出文件路径（.dot格式）	"tree.dot"
feature_names	特征名称列表	iris.feature_names
class_names	类别名称（分类问题）	["setosa", "versicolor"]
filled	是否用颜色填充节点	True
rounded	是否圆角显示	True

示例：

# 生成可视化文件（需配合Graphviz显示）
export_graphviz(
    model,
    out_file="tree.dot",
    feature_names=iris.feature_names,
    class_names=iris.target_names,
    filled=True,
    rounded=True
)
​
# 转换为PNG图片（需安装Graphviz）
!dot -Tpng tree.dot -o tree.png

3. 决策树的核心流程

1. 训练模型：

   model.fit(X_train, y_train)

2. 预测：

   y_pred = model.predict(X_test)

3. 可视化：

   • 生成.dot文件 → 用Graphviz转换为图片（如PNG）。

注意事项：

• 防止过拟合：

  • 通过max_depth、min_samples_split等参数限制树生长。

总结：

# 1. 创建模型（选基尼或熵）
model = DecisionTreeClassifier(criterion="gini", max_depth=3)
​
# 2. 训练并预测
model.fit(X, y)
y_pred = model.predict(X_new)
​
# 3. 可视化（生成.dot文件）
export_graphviz(model, out_file="tree.dot", feature_names=feature_names)

示例：

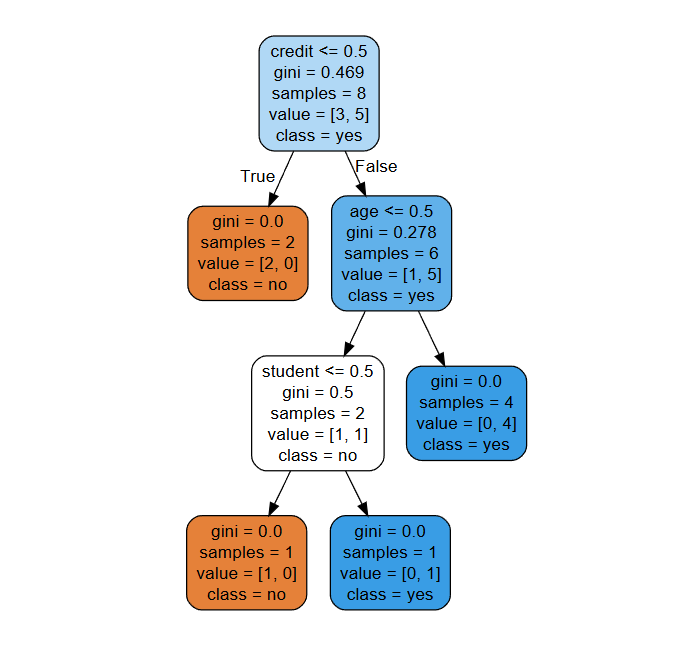
用决策树判断一个人是否会购买电脑（分类问题），特征包括：

• 年龄（age）：青年（0）、中年（1）、老年（2）

• 收入（income）：低（0）、中（1）、高（2）

• 学生（student）：否（0）、是（1）

• 信用（credit）：差（0）、好（1）

目标标签：buy（不买=0，买=1）

import pandas as pd
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.model_selection import train_test_split
# pandas: 用于数据处理和分析，这里主要用来创建和操作DataFrame
# DecisionTreeClassifier: scikit-learn中的决策树分类器
# export_graphviz: 用于将决策树导出为Graphviz格式以便可视化
# train_test_split: 用于将数据集分割为训练集和测试集

# 1. 准备数据
data = {
    "age": [0, 0, 1, 2, 2, 1, 0, 1, 2, 0],
    "income": [2, 2, 2, 1, 0, 0, 1, 1, 1, 2],
    "student": [0, 0, 0, 0, 1, 1, 1, 0, 1, 0],
    "credit": [1, 0, 1, 1, 1, 0, 1, 1, 1, 0],
    "buy": [0, 0, 1, 1, 1, 0, 1, 1, 1, 0]
}
df = pd.DataFrame(data)
X = df.drop("buy", axis=1)
y = df["buy"]
# 将字典转换为pandas DataFrame
# X包含所有特征（去掉"buy"列）
# y是目标变量（"buy"列）

# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 3. 训练决策树模型（使用基尼指数）
model = DecisionTreeClassifier(criterion="gini", max_depth=3, random_state=42)
model.fit(X_train, y_train)

# 4. 评估模型
print("测试集准确率:", model.score(X_test, y_test)) #score()方法计算模型在测试集上的准确率

# 5. 可视化决策树（需安装Graphviz）
export_graphviz(
    model,
    out_file="./buy_computer.dot",
    feature_names=["age", "income", "student", "credit"],
    class_names=["no", "yes"],
    filled=True,
    rounded=True
)
print("决策树已保存为 buy_computer.dot")

#输出：
#测试集准确率: 1.0
#决策树已保存为 buy_computer.dot

把文件”buy_computer.dot“内容粘贴到"http://webgraphviz.com/"点击"generate Graph"决策树图

二、集成学习方法-随机森林

1、算法原理

机器学习中有一种大类叫集成学习（Ensemble Learning），集成学习的基本思想就是将多个分类器组合，从而实现一个预测效果更好的集成分类器。集成算法可以说从一方面验证了中国的一句老话：三个臭皮匠，赛过诸葛亮。集成算法大致可以分为：Bagging，Boosting 和 Stacking 三大类型。

（1）每次有放回地从训练集中取出 n 个训练样本，组成新的训练集；

（2）利用新的训练集，训练得到M个子模型；

（3）对于分类问题，采用投票的方法，得票最多子模型的分类类别为最终的类别；

什么是随机森林？

一句话：随机森林就是一群决策树投票做决定！

• 比如：要判断一个人是不是好人，让100个决策树（100个"小法官"）各自判断，最后少数服从多数。

• 随机森林：

  1. 随机选数据：每棵树只看部分样本（比如100人里随机抽80人）。

  2. 随机选特征：每棵树只用部分特征（比如年龄、收入、职业中随机选2个）。

  3. 集体投票：综合所有树的意见，避免个别树的偏见。

核心原理

• 两个随机：

  1. 数据随机：每棵树训练时，随机抽取样本（有放回）。

     • 比如：原始数据是[A,B,C,D]，可能抽到[A,B,B,D]（B被抽到两次）。

  2. 特征随机：每棵树分裂时，只随机用部分特征。

     • 比如：年龄、工资、学历中，随机选"年龄+工资"来分裂。

• 最终结果：

  • 分类问题：投票（哪类票数多就选谁）。

  • 回归问题：取平均值（比如预测房价，所有树的预测取平均）。

2、SKlearn API

sklearn.ensemble.RandomForestClassifier 

RandomForestClassifier 是 scikit-learn 提供的随机森林分类器实现，它通过构建多个决策树并进行集成来提高模型的准确性和鲁棒性。以下是该分类器的主要参数及其详细说明：

1. n_estimators（决策树的数量）

• 作用：指定森林中决策树的数量。

• 默认值：100。

• 如何选择：

  • 增加树的数量可以提高模型的稳定性，但计算成本也会增加。

  • 通常选择 100~500，具体取决于数据集大小和计算资源。

  • 可以通过交叉验证（如 GridSearchCV）调优。

2. criterion（分裂标准）

• 作用：决定决策树如何选择最优分裂特征。

• 可选值：

  • "gini"（默认）：基尼不纯度（Gini impurity），计算更快。

  • "entropy"：信息增益（Information gain），理论更严谨，但计算稍慢。

• 如何选择：

  • 大多数情况下 "gini" 足够，计算效率更高。

  • 如果对模型解释性要求高，可以尝试 "entropy"。

3. max_depth（树的最大深度）

• 作用：限制每棵决策树的最大深度，防止过拟合。

• 默认值：None（不限制，直到所有叶子节点纯或达到 min_samples_split）。

• 如何选择：

  • 如果数据量较大，可以适当增加（如 10~30）。

  • 如果数据量较小，建议限制深度（如 3~10），避免过拟合。

  • 可通过交叉验证调优。

4. min_samples_split（节点分裂的最小样本数）

• 作用：如果一个节点的样本数少于该值，则不再分裂。

• 默认值：2（即每个节点至少需要 2 个样本才能分裂）。

• 如何选择：

  • 增大该值可以防止过拟合（如设为 5 或 10）。

  • 对于大数据集，可以保持默认或稍大一些。

5. min_samples_leaf（叶子节点的最小样本数）

• 作用：每个叶子节点至少需要的样本数。

• 默认值：1。

• 如何选择：

  • 增大该值可以防止过拟合（如 3 或 5）。

  • 如果数据噪声较多，可以适当增加。

6.max_features（每次分裂考虑的最大特征数）

• 作用：控制每棵树分裂时的特征随机性。

• 可选值：

  • "auto"（默认）：max_features = sqrt(n_features)（分类问题）或 n_features（回归问题）。

  • "sqrt"：等同于 "auto"。

  • "log2"：max_features = log2(n_features)。

  • 整数或浮点数：直接指定特征数量或比例。

• 如何选择：

  • 通常使用默认值即可。

  • 如果特征非常多（如 >100），可以尝试 "log2" 或更小的值。

7. bootstrap（是否使用自助采样）

• 作用：是否对样本进行有放回抽样（bootstrap sampling）。

• 默认值：True（随机森林的标准做法）。

• 如果设为 False：

  • 每棵树使用全部样本（类似 Bagging，但特征仍随机）。

  • 适用于小数据集，但可能降低模型的多样性。

8. random_state（随机种子）

• 作用：控制随机性，使结果可复现。

• 默认值：None（每次运行结果可能不同）。

• 如何选择：

  • 设为固定值（如 42）可以确保每次运行结果一致。

方法	作用
fit(X, y)	训练模型。
predict(X)	预测类别。
predict_proba(X)	预测类别概率。
score(X, y)	计算准确率。

示例：

（鸢尾花）

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据
data = load_iris()
X, y = data.data, data.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化随机森林
model = RandomForestClassifier(
    n_estimators=100,
    criterion="gini",
    max_depth=5,
    min_samples_split=2,
    random_state=42
)

# 训练
model.fit(X_train, y_train)

# 评估
print("测试集准确率:", model.score(X_test, y_test))

# 输出：
# 测试集准确率: 1.0