参考自TI的《A Single-Supply Op-AmpCircuit Collection》

---

前言

提示：这里可以添加本文要记录的大概内容：

例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。

---

提示：以下是本篇文章正文内容，下面案例可供参考

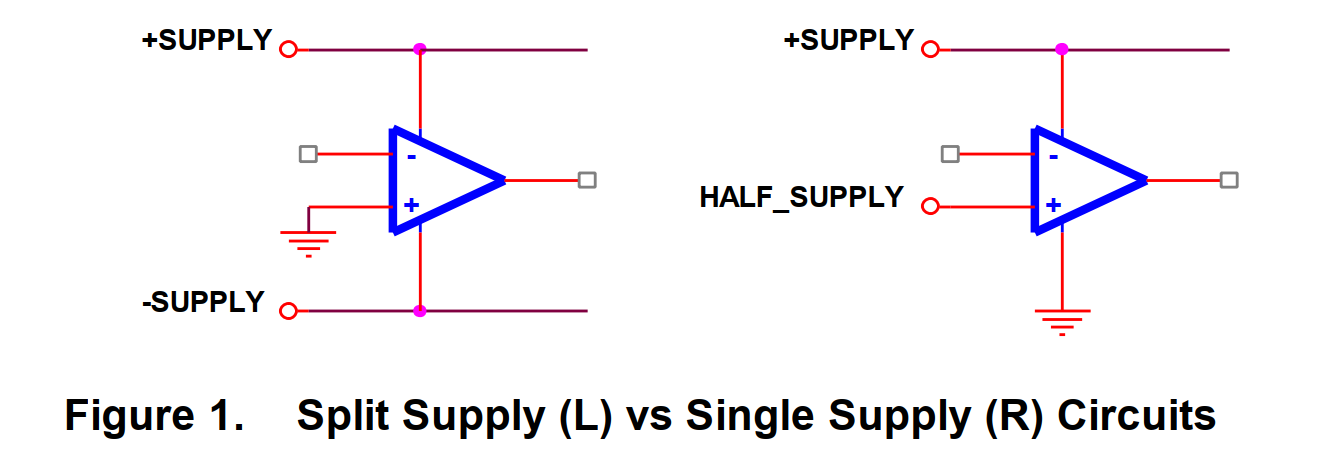
一、单电源供电和双电源供电的区别

所有的运算放大器都有两个电源引脚， 一般在资料中， 它们的标识是 VCC＋和 VCC－(或者是VSS)，但是有些时候它们的标识是 VCC＋和 GND。这是因为有些数据手册的作者企图将这种标识的差异作为单电源运放和双电源运放的区别。但是，这并不是说他们就一定要那样使用――他们可能可以工作在其他的电压下。

二、如何单电源

1、虚地

单电源工作的运放需要外部提供一个虚地，通常情况下，这个电压是 VCC/2，图二的电路可以用来产生 VCC/2 的电压，但是他会降低系统的低频特性
R1 和 R2 是等值的，通过电源允许的消耗和允许的噪声来选择，电容 C1 是一个低通滤波器，用来减少从电源上传来的噪声。在有些应用中可以忽略缓冲运放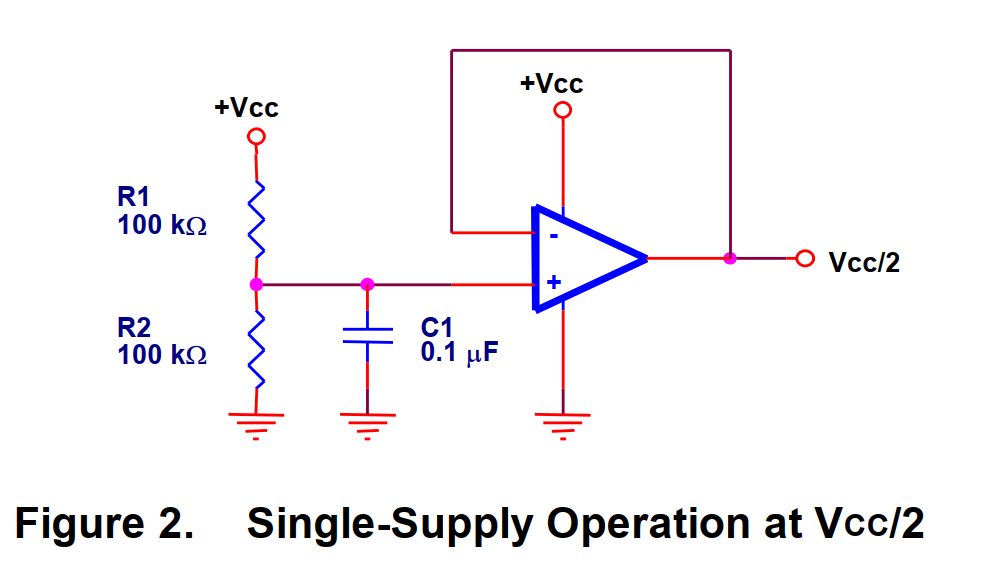

2、交流耦合

虚地是大于电源地的直流电平，这是一个小的、局部的地电平，这样就产生了一个
电势问题：输入和输出电压一般都是参考电源地的，如果直接将信号源的输出接到运放的输入端，这将会产生不可接受的直流偏移。如果发生这样的事情，运放将不能正确的响应输入电压，因为这将使信号超出运放允许的输入或者输出范围。解决这个问题的方法将信号源和运放之间用交流耦合。使用这种方法，输入和输出
器件就都可以参考系统地，并且运放电路可以参考虚地。当不止一个运放被使用时，如果碰到以下条件级间的耦合电容就不是一定要使用：
第一级运放的参考地是虚地
第二级运放的参考第也是虚地
这两级运放的每一级都没有增益。任何直流偏置在任何一级中都将被乘以增益，并
且可能使得电路超出它的正常工作电压范围。

三、基本单电源电路

1、放大器

放大电路有两个基本类型：同相放大器和反相放大器。他们的交流耦合版本如图三所示。
对于交流电路，反向的意思是相角被移动 180 度。这种电路采用了耦合电容――Cin。 Cin被用来阻止电路产生直流放大，这样电路就只会对交流产生放大作用。如果在直流电路中，Cin 被省略，那么就必须对直流放大进行计算。
在高频电路中，不要违反运放的带宽限制，这是非常重要的。实际应用中，一级放大电路的增益通常是 100 倍（40dB），再高的放大倍数将引起电路的振荡，除非在布板的时候就非常注意。如果要得到一个放大倍数比较的大放大器，用两个等增益的运放或者多个等增益运放比用一个运放的效果要好的多。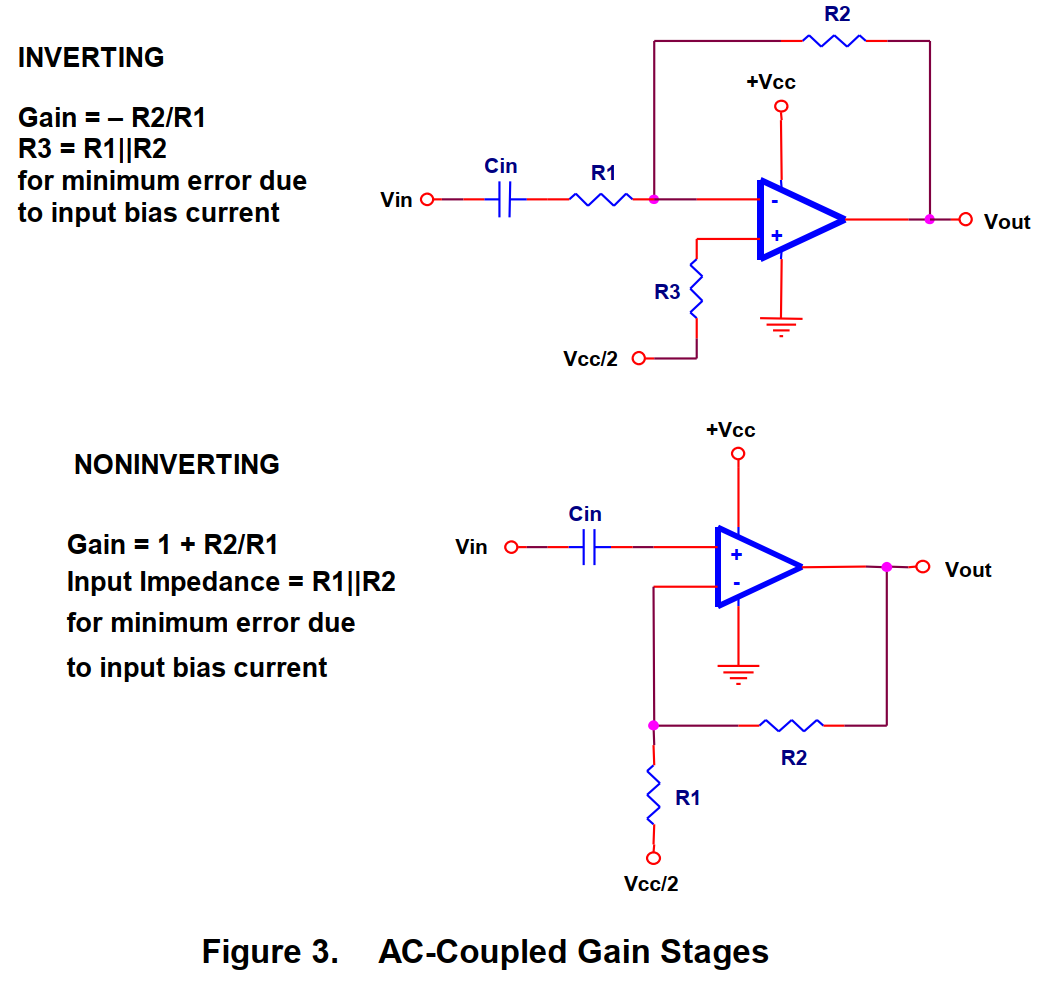

2、加法器

图七是一个反相加法器，他是一个基本的音频混合器。但是该电路的很少用于真正的音频混合器。因为这会逼近运放的工作极限，实际上我们推荐用提高电源电压的办法来提高动态范围。同相加法器是可以实现的， 但是是不被推荐的。 因为信号源的阻抗将会影响电路的增益。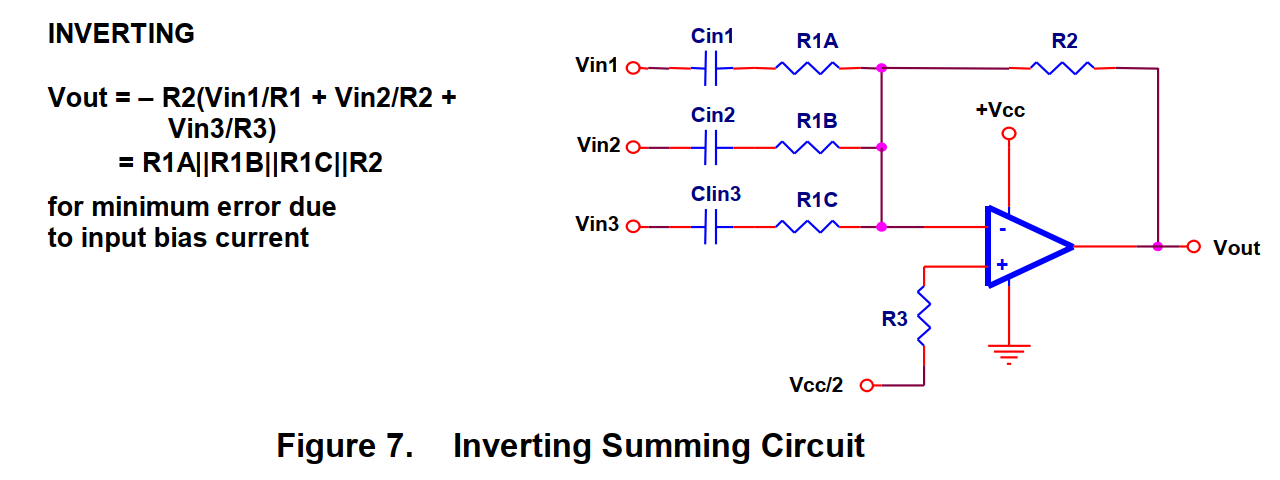

3、减法器

就像加法器一样，图八是一个减法器。一个通常的应用就是用于去除立体声磁带中的原唱而留下伴音（在录制时两通道中的原唱电平是一样的，但是伴音是略有不同的）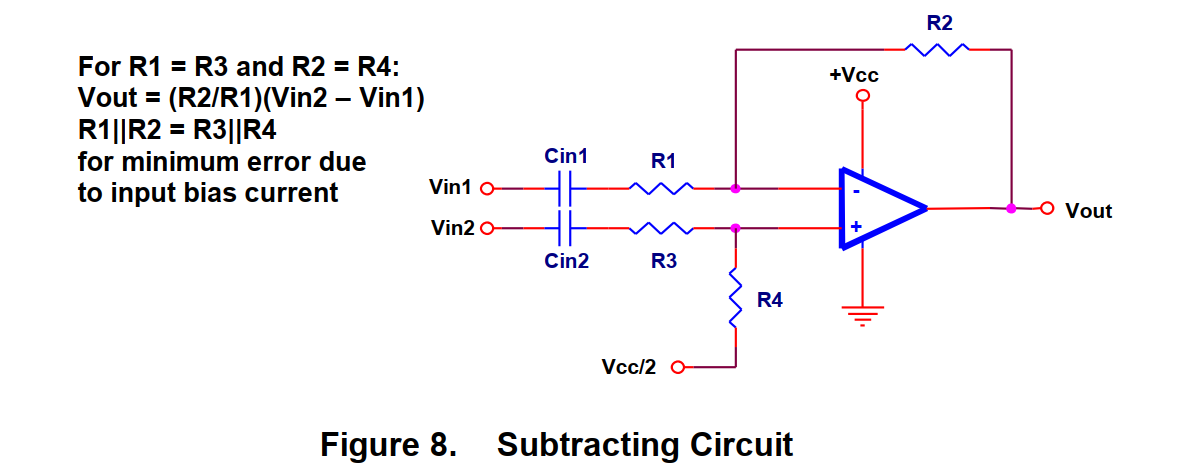

4、仪表放大器

参考
\https://www.bilibili.com/video/BV1Gt411b7Zq?spm_id_from=333.788.videopod.episodes&vd_source=1cb0531b25720f8b7430744365abec0f&p=40
推荐郑益慧老师的模电，讲的特别清楚

这个电路是基本的仪用放大电路，其他的仪用放大器也如图中所示，这里的输入端也使用了单电源供电。这个电路实际上是一个单电源的应变仪。这个电路的缺点是需要完全相等的电阻，否则这个电路的共模抑制比将会很低

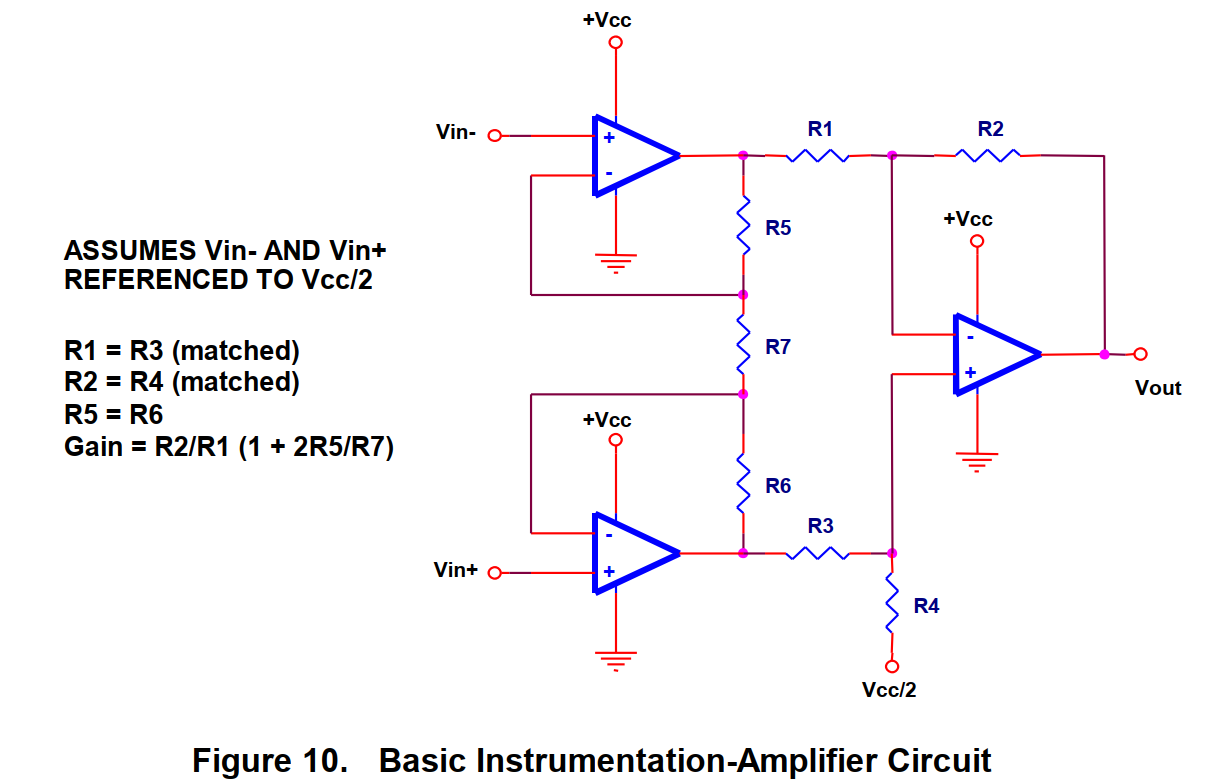
有利于在共模干扰不变的条件下增加差模输出

5、有源滤波器

在很多情况中，为了阻挡由于虚地引起的直流电平，在运放的输入端串入了电容。这个电容实际上是一个高通滤波器，在某种意义上说，像这样的单电源运放电路都有这样的电容。设计者必须确定这个电容的容量必须要比电路中的其他电容器的容量大 100 倍以上。 这样才可以保证电路的幅频特性不会受到这个输入电容的影响。如果这个滤波器同时还有放大作用，这个电容的容量最好是电路中其他电
容容量的 1000 倍以上。如果输入的信号早就包含了 VCC/2 的直流偏置，这个电容就可以省略。
这些电路的输出都包含了 VCC/2 的直流偏置，如果电路是最后一级，那么就必须串入输出电容。这里有一个有关滤波器设计的协定，这里的滤波器均采用单电源供电的运放组成。滤波器的实现很简单，但是以下几点设计者必须注意：
滤波器的拐点（中心）频率
滤波器电路的增益
带通滤波器和带阻滤波器的的 Q 值， 低通和高通滤波器的类型（Butterworth、Chebyshev、Bessell）。
不幸的是要得到一个完全理想的滤波器是无法用一个运放组成的。即使可能，由于各个元件之间的负杂互感而导致设计者要用非常复杂的计算才能完成滤波器的设计。 通常对波形的控制要求越复杂就意味者需要更多的运放，这将根据设计者可以接受的最大畸变来决定。或者可以通过几次实验而最终确定下来。如果设计者希望用最少的元件来实现滤波器，那么就别无选择，只能使用传统的滤波器，通过计算就可以得到了

（1）低通

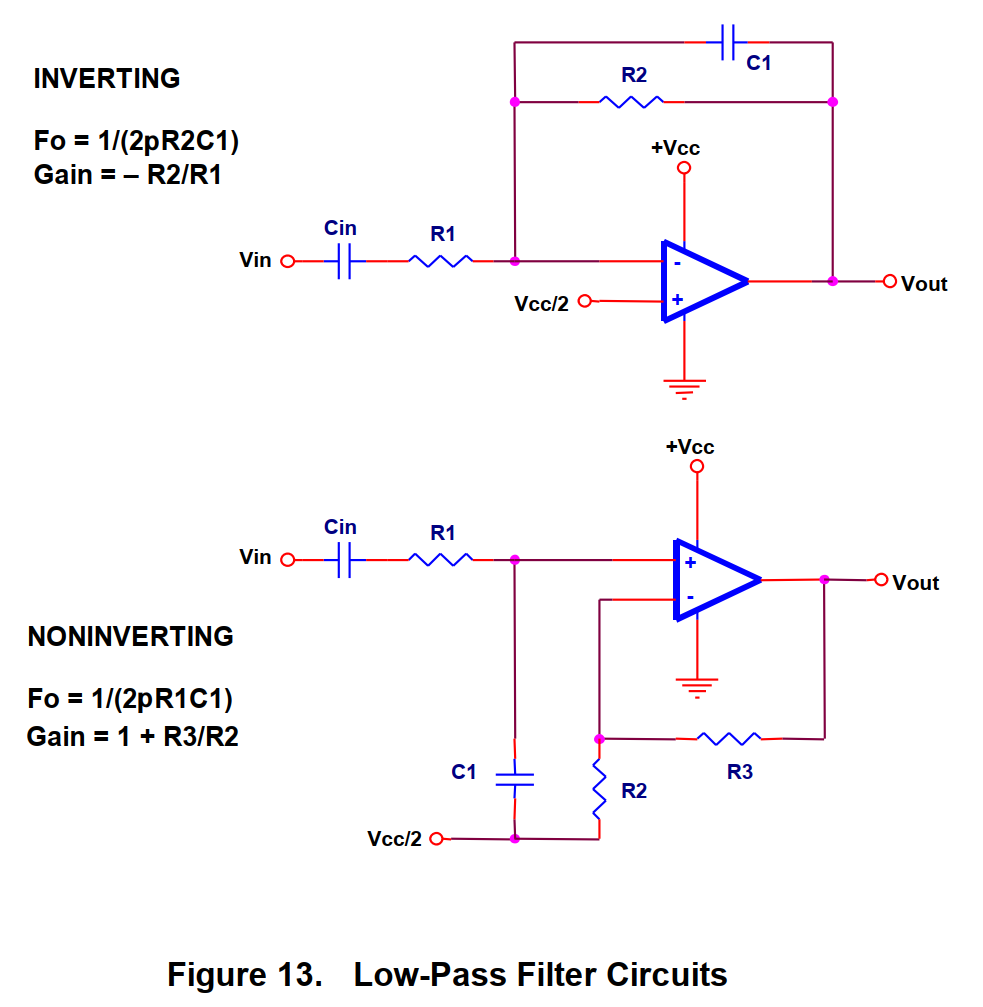
（2）高通

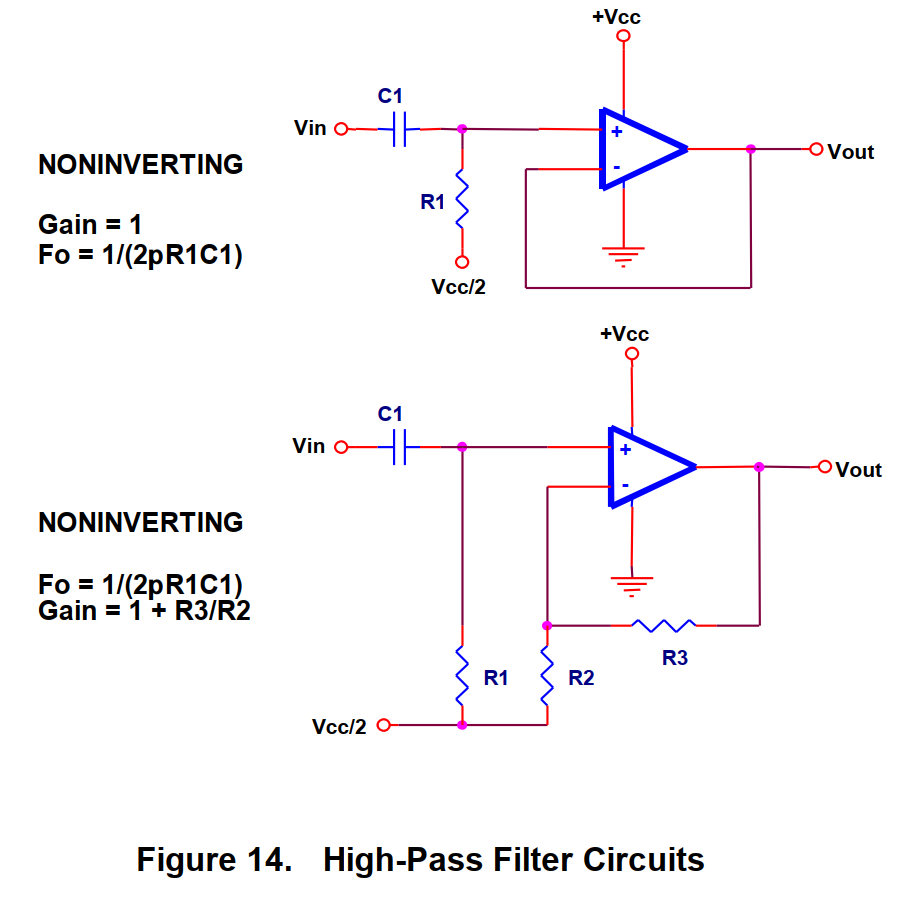
（3）全通

全通滤波器对所有的频率都有相同的增益，但是他可以改变信号的相角，他同时也用来做相角修正电路。图十五中的电路对频率是 F 的信号有 90 度的相移，对直流的相移是0 度，对高频的相移是 180 度。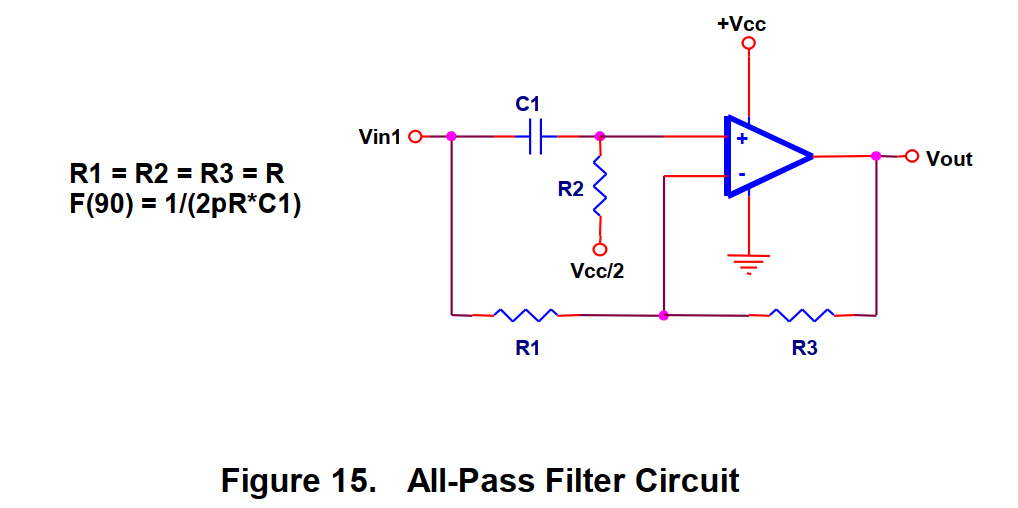

六、二阶有源滤波电路

二阶滤波电路一般用他们的发明者命名。他们中的少数几个至今还在使用。有一些二阶滤波器的拓扑结构可以组成低通、高通、带通、带阻滤波器，有些则不行。这里没有列出所有的滤波器拓扑结构，只是将那些容易实现和便于调整的列了出来。
二阶滤波器有 40dB 每倍频的幅频特性。通常的同一个拓扑结构组成的带通和带阻滤波器使用相同的元件来调整他们的Q值，而且他们使滤波器在 Butterworth 和 Chebyshev 滤波器之间变化。必须要知道只有Butterworth 滤波器可以准确的计算出拐点频率， Chebyshev 和 Bessell 滤波器只能在Butterworth 滤波器的基础上做一些微调。
我们通常用的带通和带阻滤波器有非常高的 Q 值。如果需要实现一个很宽的带通或者带阻滤波器就需要用高通滤波器和低通滤波器串连起来。 对于带通滤波器的通过特性将是这两个滤波器的交叠部分，对于带阻滤波器的通过特性将是这两个滤波器的不重叠部分。

（1）Sallen－Key

Sallen-Key 滤波器是一种流行的、广泛应用的二阶滤波器。他的成本很低，仅需要一个运放和四个无源器件组成。但是换成 Butterworth 或 Chebyshev 滤波器就不可能这么容易的调整了。
这个电路是一个单位增益的电路，改变 Sallen－Key 滤波器的增益同时就改变了滤波器的幅频特性和类型。实际上 Sallen－Key 滤波器就是增益为 1 的 Butterworth 滤波器。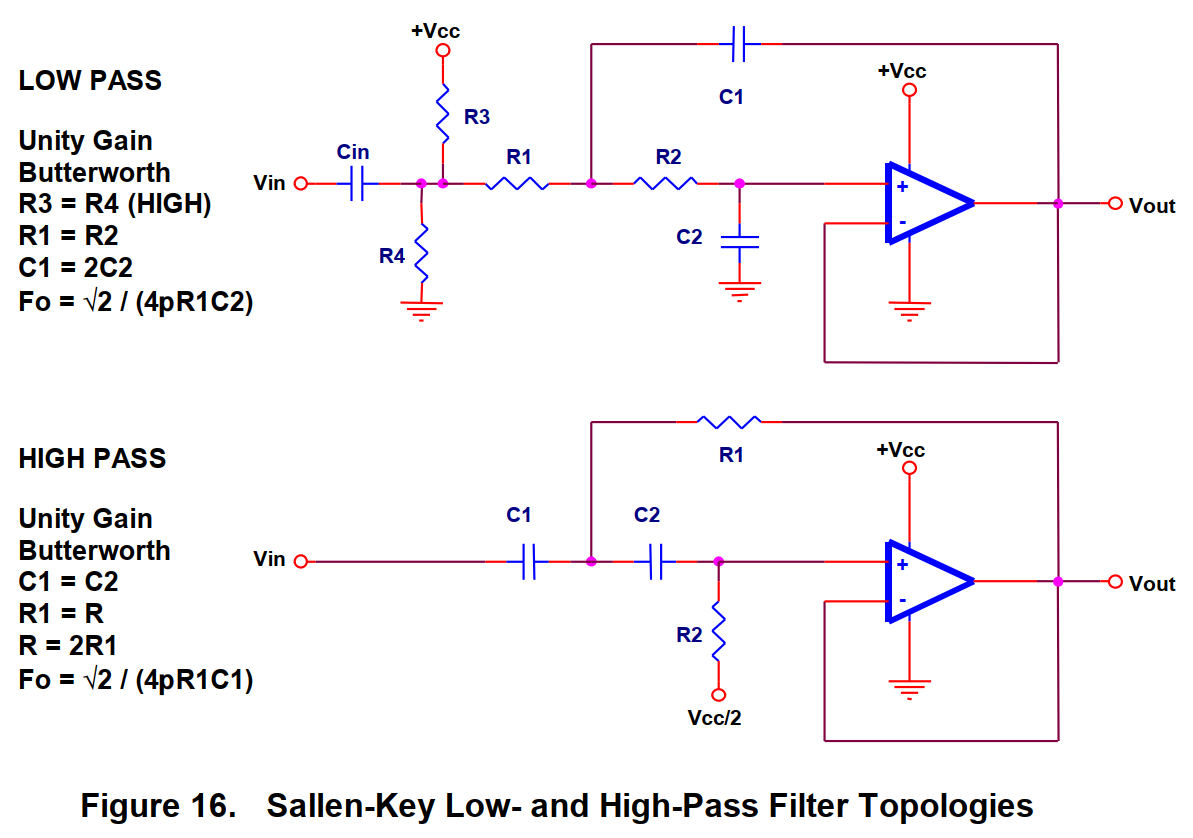

---

其他的复杂难以使用，具体请参考：
《A Single-Supply Op-AmpCircuit Collection》