无监督学习

摘要

本周探讨了无监督学习中的几种关键方法，包括高斯混合模型（GMM）、聚类算法（如K-Means和Mean Shift）以及受限玻尔兹曼机（RBM）。高斯混合模型利用概率模型来拟合数据，并通过可视化展示了其对二维数据集的预测轮廓。聚类部分涵盖了多种算法的性能和局限性，如K-Means和Mean Shift，并提供了具体示例。最后，还介绍了受限玻尔兹曼机的工作原理及其在特征学习中的应用。

abstract

This week explores several key methods in unsupervised learning, including Gaussian mixture models (GMM), clustering algorithms such as K-Means and Mean Shift, and restricted Boltzmann machines (RBM). The Gaussian mixture model uses a probabilistic model to fit the data and visualizes its predictive profile for a two-dimensional dataset. The clustering section covers the performance and limitations of various algorithms, such as K-Means and Mean Shift, and provides concrete examples. Finally, the working principle of restricted Boltzmann machine and its application in feature learning are introduced.

1.高斯混合模型

高斯混合模型是一种概率模型，它假设所有数据点是由有限数量的、具有未知参数的高斯分布。人们可以想到混合模型作为推广 k-means 聚类以合并，有关数据协方差结构的信息以及潜在高斯的中心。
以下演示如何生成二维数据集、拟合一个高斯混合模型并可视化模型预测的负对数似然轮廓图。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import LogNorm

from sklearn import mixture

n_samples = 300

# 随机种子以确保结果的可重复性
np.random.seed(0)

# 生成中点（20，20）的高斯分布数据
shifted_gaussian = np.random.randn(n_samples, 2) + np.array([20, 20])

# 生成“拉伸”高斯分布的数据，通过一个变换矩阵C使数据沿特定方向拉伸，然后乘以随机高斯噪声。
C = np.array([[0.0, -0.7], [3.5, 0.7]])
stretched_gaussian = np.dot(np.random.randn(n_samples, 2), C)

# 合并数据集
X_train = np.vstack([shifted_gaussian, stretched_gaussian])

# 拟合GMM模型
clf = mixture.GaussianMixture(n_components=2, covariance_type="full")
clf.fit(X_train)

# 计算并绘制
x = np.linspace(-20.0, 30.0)
y = np.linspace(-20.0, 40.0)
X, Y = np.meshgrid(x, y)
XX = np.array([X.ravel(), Y.ravel()]).T
Z = -clf.score_samples(XX)
Z = Z.reshape(X.shape)

CS = plt.contour(
    X, Y, Z, norm=LogNorm(vmin=1.0, vmax=1000.0), levels=np.logspace(0, 3, 10)
)
CB = plt.colorbar(CS, shrink=0.8, extend="both")
plt.scatter(X_train[:, 0], X_train[:, 1], 0.8)

plt.title("Negative log-likelihood predicted by a GMM")
plt.axis("tight")
plt.show()

运行结果：

1.1 高斯混合

高斯混合对象实现了期望最大化（EM）算法，用于拟合高斯混合模型。它还可以为多元模型绘制置信椭球，并计算贝叶斯信息准则，以评估数据中的聚类数。提供了一个GaussianMixture.fit方法，从训练数据中学习高斯混合模型。给定测试数据，它可以使用GaussianMixture.predict方法将每个样本分配到其最可能属于的高斯分布。
在鸢尾花数据集上使用各种GMM协方差类型在训练数据和保留的测试数据上绘制预测标签。我们比较了球形、对角、全和绑定协方差矩阵的GMM，按照性能逐渐递增的顺序。尽管一般来说全协方差的表现最好，但在小数据集上容易过拟合，并且在保留的测试数据上不太能泛化。
在图中，训练数据用点表示，而测试数据用叉表示。鸢尾花数据集是四维的。这里只展示了前两个维度，因此某些点在其他维度上是分开的。

1.2 变分贝叶斯高斯混合

变分贝叶斯高斯混合具有变分推理算法的高斯混合模型。变分推断是期望最大化的一种扩展，它最大化模型依据的下界（包括先验）而不是数据似然。变分方法背后的原理与期望最大化相同（即两者都是迭代算法，交替寻找每个点由每个混合生成的概率，并将混合拟合到这些指定点上），但变分方法通过整合来自先验分布的信息添加了正则化。这避免了期望最大化解中的奇异性，但引入了对模型的一些微妙偏差。推断的速度通常明显较慢，但通常不会慢到让使用变得不切实际。
由于其贝叶斯性质，变分算法需要更多的超参数比较期望最大化，其中最重要的是浓度参数。指定一个较低的值，对于浓度的先验将使模型将大部分权重放在少数几个组件，并将其余组件的权重设置得非常接近于零。
绘制使用期望最大化（GaussianMixture 类）和变分推断获得的两个高斯混合的置信椭球体。

import itertools
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy import linalg
from sklearn import mixture

color_iter = itertools.cycle(["navy", "b", "cornflowerblue", "gold", "darkorange"])

def plot_results(X, Y_, means, covariances, index, title):
    splot = plt.subplot(2, 1, 1 + index)
    for i, (mean, covar, color) in enumerate(zip(means, covariances, color_iter)):
        v, w = linalg.eigh(covar)
        v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
        u = w[0] / linalg.norm(w[0])
        if not np.any(Y_ == i):
            continue
        plt.scatter(X[Y_ == i, 0], X[Y_ == i, 1], 0.8, color=color)

        # 展示高斯分布的轮廓
        angle = np.arctan(u[1] / u[0])
        angle = 180.0 * angle / np.pi  # convert to degrees
        ell = mpl.patches.Ellipse(mean, v[0], v[1], angle=180.0 + angle, color=color)
        ell.set_clip_box(splot.bbox)
        ell.set_alpha(0.5)
        splot.add_artist(ell)

    plt.xlim(-9.0, 5.0)
    plt.ylim(-3.0, 6.0)
    plt.xticks(())
    plt.yticks(())
    plt.title(title)
    
n_samples = 500

np.random.seed(0)
C = np.array([[0.0, -0.1], [1.7, 0.4]])
X = np.r_[
    np.dot(np.random.randn(n_samples, 2), C),
    0.7 * np.random.randn(n_samples, 2) + np.array([-6, 3]),
]

# 创建一个5个成分的GMM模型，并设定协方差类型为"full"（完全协方差）
gmm = mixture.GaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(X, gmm.predict(X), gmm.means_, gmm.covariances_, 0, "Gaussian Mixture")

# 创建一个5个成分的DP-GMM模型，同样设定协方差类型为"full"
dpgmm = mixture.BayesianGaussianMixture(n_components=5, covariance_type="full").fit(X)
plot_results(
    X,
    dpgmm.predict(X),
    dpgmm.means_,
    dpgmm.covariances_,
    1,
    "Bayesian Gaussian Mixture with a Dirichlet process prior",
)
plt.show()

这两个模型都可以访问五个组件来拟合数据。请注意，期望最大化模型必然会使用所有五个组件，而变分推断模型实际上只会使用适合良好拟合所需的数量。在这里，我们可以看到期望最大化模型会随意拆分一些组件，因为它试图拟合过多的组件，而狄利克雷过程模型则会自动调整状态的数量。
这个例子没有体现出来，因为我们处于低维空间，但狄利克雷过程模型的另一个优点是，即使每个聚类的样本数少于数据的维度，它也能有效拟合完整的协方差矩阵，这是因为推断算法的正则化特性。

2.聚类

2.1 所有的聚类方法

这个例子展示了不同聚类算法在“有趣”但仍然是二维的数据集上的特征。除了最后一个数据集外，每组数据集和算法的参数都经过调整，以产生良好的聚类结果。有些算法对参数值的敏感度比其他算法高。
最后一个数据集是聚类的“无效”情况的例子：数据是同质的，没有好的聚类。对于这个例子，无效数据集使用的参数与上面行中的数据集相同，这表明参数值与数据结构之间不匹配。
虽然这些例子提供了一些关于算法的直觉，但这种直觉可能不适用于非常高维的数据。

2.2 K-均值

该算法通过尝试将样本分隔成 n 个样本来聚类数据方差相等的群，最小化称为惯性的标准或簇内平方和（见下面的公式）。这个算法需要指定聚类的数量。它可以很好地扩展到大量样品，并具已在许多不同领域的广泛应用领域中使用。
k-means算法将一组样本划分为不相交的聚类，每个聚类都由聚类中样本的平均值来描述。这些均值通常称为聚类 “质心”。
$$\sum _{i=0}^n\underset{{\mu }_j\in C}{\min }(||x_i-{\mu }_j|{|}^2)$$
K-means算法的目标是选择中心点，使得每个簇内部的平方误差总和（即惯性）最小化。简单来说，算法通过不断调整中心点的位置，以确保簇内的数据点尽可能接近其对应的中心点，从而提高聚类的质量。
下面是一个K-均值假设的证明：
首先是数据生成

import numpy as np

from sklearn.datasets import make_blobs

n_samples = 1500
random_state = 170
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]

X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_aniso = np.dot(X, transformation)  # Anisotropic blobs
X_varied, y_varied = make_blobs(
    n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
)  # Unequal variance
X_filtered = np.vstack(
    (X[y == 0][:500], X[y == 1][:100], X[y == 2][:10])
)  # Unevenly sized blobs
y_filtered = [0] * 500 + [1] * 100 + [2] * 10

其可视化结果如下

之前生成的数据现在用于展示KMeans在以下场景中的表现：
非最优的聚类数量：在实际情况下，没有唯一定义的真实聚类数量。必须根据数据驱动的标准和目标来决定合适的聚类数量。
各向异性分布的簇：k-means的目标是最小化样本到其分配的聚类中心的欧几里得距离。因此，k-means更适合各向同性和正态分布的聚类（即球形高斯分布）。
方差不均：k-means相当于对k个高斯分布的“混合”取最大似然估计，这些高斯分布有相同的方差但可能有不同的均值。
大小不均的簇：关于k-means的理论结果并没有说明它需要类似的聚类大小才能表现良好，但最小化欧几里得距离确实意味着问题越稀疏和高维，运行算法时使用不同的聚类中心种子以确保全局最小惯性就越必要。

2.3 均值偏移

“均值偏移：一种稳健的方法 特征空间分析”。
下面是均值偏移的一个例子：

import numpy as np

from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs
# 生成样本数据
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
# 使用 MeanShift 计算聚类
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)

ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_

labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)

print("number of estimated clusters : %d" % n_clusters_)

# 绘图
import matplotlib.pyplot as plt

plt.figure(1)
plt.clf()

colors = ["#dede00", "#377eb8", "#f781bf"]
markers = ["x", "o", "^"]

for k, col in zip(range(n_clusters_), colors):
    my_members = labels == k
    cluster_center = cluster_centers[k]
    plt.plot(X[my_members, 0], X[my_members, 1], markers[k], color=col)
    plt.plot(
        cluster_center[0],
        cluster_center[1],
        markers[k],
        markerfacecolor=col,
        markeredgecolor="k",
        markersize=14,
    )
plt.title("Estimated number of clusters: %d" % n_clusters_)
plt.show()

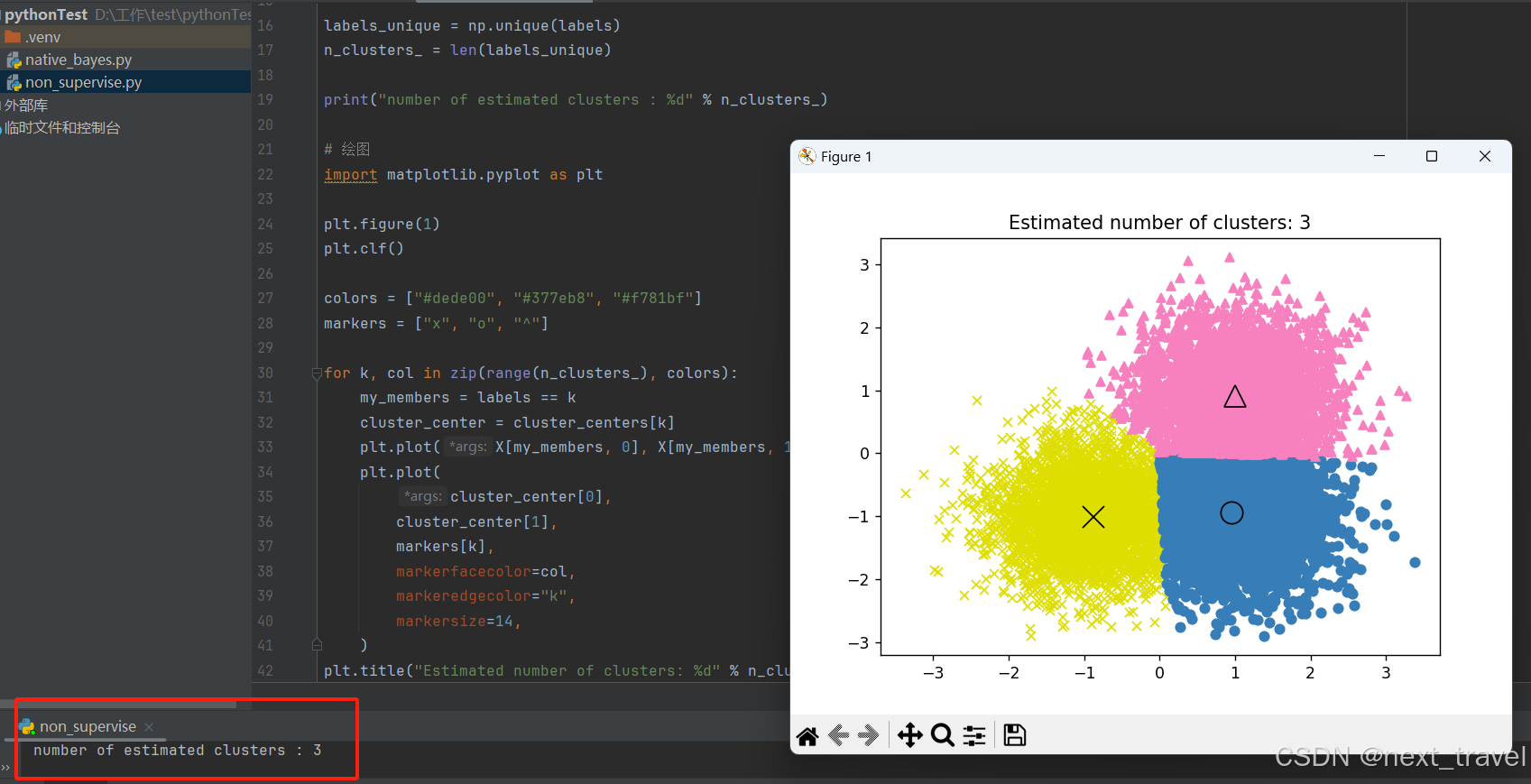
上面三个数据点展示了如何使用 scikit-learn 库中的 MeanShift 算法对一组数据点进行聚类分析。

3.神经网络模型（无监督）

3.1 受限玻尔兹曼机

限制玻尔兹曼机（RBM）是一种基于概率模型的无监督非线性特征学习器。通过RBM或多个RBM的层次提取的特征在输入线性分类器时，比如线性SVM或感知机，通常能取得不错的结果。
该模型对输入的分布有假设。目前，scikit-learn仅提供伯努利RBM，它假设输入要么是二进制值，要么是介于0和1之间的值，每个值编码了特定特征被启用的概率。
RBM试图通过特定的图形模型最大化数据的似然性。所使用的参数学习算法（随机最大似然）防止表示远离输入数据，从而使其捕捉到有趣的规律，但这也使得模型在小数据集上不够有效，并通常不适合用于密度估计。
这种方法因使用独立RBM的权重来初始化深度神经网络而变得流行，这个方法被称为无监督预训练。

3.1.1 图形化和参数

RBM的图形模型是一个全连接的二分图。

节点是随机变量，其状态依赖于与其连接的其他节点的状态。因此，该模型由连接的权重参数化，以及每个可见和隐藏单元的一个截距（偏置）项，为了简单起见，这些在图中被省略。
能量函数衡量联合赋值的质量：
$$E(\mathbf{v},\mathbf{h})=-\sum _i\sum _j{w}_{ij}{v}_i{h}_j-\sum _i{b}_i{v}_i-\sum _j{c}_j{h}_j$$
在上面的公式中，𝑏 和 𝑐 分别是可见层和隐藏层的截距向量。模型的联合概率是根据能量来定义的：
$$P(\mathbf{v},\mathbf{h})=\frac{e^{-E(\mathbf{v},\mathbf{h})}}{Z}$$
限制一词指的是模型的双重结构，这种结构禁止隐藏单元之间或可见单元之间的直接交互。这意味着假设了以下条件独立性
$$\begin{gathered} h_i\perp h_j|\mathbf{v} \\ {v}_i\perp v_j|\mathbf{h} \end{gathered}$$

3.1.2 伯努利限制玻尔兹曼机

在伯努利RBM中，所有单元都是二元随机单元。这意味着输入数据应该是二进制的，或者是在0和1之间的实值，表示可见单元开启或关闭的概率。这是一种很好的字符识别模型，因为它关注哪些像素是活跃的，哪些不是。但对于自然场景图像，它就不太适用了，因为背景、深度以及相邻像素倾向于取相同值的原因。

每个单元的条件概率分布由其接收到的输入的逻辑 sigmoid 激活函数给出：
$$\begin{gathered} P(v_i=1|\mathbf{h})=\sigma (\sum _j{w}_{ij}{h}_j+b_i) \\ P(h_i=1|\mathbf{v})=\sigma (\sum _i{w}_{ij}{v}_i+c_j) \end{gathered}$$

其中 𝜎 是逻辑 sigmoid 函数：
$$\sigma (x)=\frac{1}{1+e^{-x}}$$

3.1.3 随机最大似然学习

在BernoulliRBM中实现的训练算法被称为随机最大似然（SML）或持久对比散度（PCD）。直接优化最大似然是不可行的，因为数据似然的形式：
$$\log P(v)=\log \sum _h{e}^{-E(v,h)}-\log \sum _{x,y}{e}^{-E(x,y)}$$

为了简单起见，上面的方程是为单个训练样本写的。关于权重的梯度由两个项组成，分别对应于上述的正梯度和负梯度，因为它们的符号不同。在这个实现中，梯度是通过小批量样本来估计的。
说明
1.在最大化对数似然时，正梯度使模型更倾向于与观察到的训练数据兼容的隐藏状态。由于RBM的二分结构，这个计算是高效的。但是负梯度是不可处理的。它的目标是降低模型偏好的联合状态的能量，从而使其更贴近数据。可以通过马尔可夫链蒙特卡洛方法使用块吉布斯采样来近似，方法是迭代地在给定其他状态的情况下对每个𝑣和ℎ进行采样，直到链混合。以这种方式生成的样本有时被称为幻想粒子。这种方法效率不高，而且很难判断马尔可夫链是否混合。
2.对比散度方法建议在经过少量迭代后停止链，通常甚至只需 1 次。这种方法速度快且方差低，但样本与模型分布相差较远。

持久对比散度解决了这个问题。在每次需要梯度时，而不是重新开始一个新的链并仅执行一次吉布斯采样步骤，PCD 保持一定数量的链（幻想粒子），在每次权重更新后进行 𝑘 次吉布斯步骤更新。这允许粒子更彻底地探索空间。

4.总结

本周深入探讨了机器学习中的无监督学习技术，重点关注高斯混合模型（GMM）、聚类方法（例如K-Means和Mean Shift）以及受限玻尔兹曼机（RBM）。
1.高斯混合模型是一种概率模型，用于拟合数据集，假设所有数据点来自有限数量的高斯分布。文章中展示了如何使用GMM来拟合二维数据，并通过负对数似然轮廓图进行了可视化。此外，还介绍了变分贝叶斯高斯混合模型，它使用变分推理算法进行拟合，与传统的期望最大化算法相比，增加了正则化效果。
2.聚类算法部分展示了K-Means和Mean Shift算法的性能特点。K-Means通过最小化簇内平方误差总和来划分数据，而Mean Shift则基于数据点密度进行聚类，能够自动确定聚类的数量。文章中通过一系列示例数据集比较了这些算法的性能。
3.受限玻尔兹曼机是一种无监督的非线性特征学习器，能够通过特定的概率模型来最大化数据的似然性。RBM特别适用于二元数据，并通过逻辑sigmoid激活函数来定义条件概率分布。文章中讨论了RBM的图形模型结构以及随机最大似然的学习方法，该方法通过持久对比散度算法进行优化。