一、简述SIFT特征提取与检索
1999年David G.Lowe教授总结了基于特征不变技术的检测方法,在图像尺度 空间基础上,提出了对图像缩放、旋转保持不变性的图像局部特征描述算子 -SIFT(尺度不变特征变换),该算法在2004年被加以完善。
二、SIFT特征提取与检索原理
SIFT算法的实质可以归为在不同尺度空间上查找特征点(关键点)的问题。
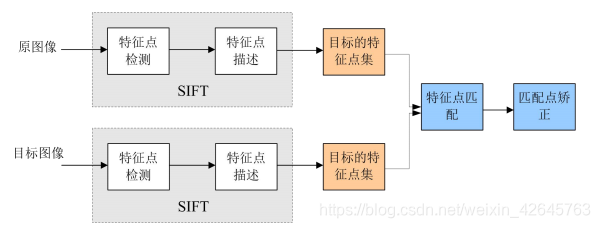
SIFT算法实现特征匹配主要有三个流程,
1、提取关键点;
2、对关键点附加 详细的信息(局部特征),即描述符;
3、通过特征点(附带上特征向量的关 键点)的两两比较找出相互匹配的若干对特征点,建立景物间的对应关系。
关键点(特征点)
这些点是一些十分突出的点不会因光照、尺度、旋转等因素的改变而消 失,比如角点、边缘点、暗区域的亮点以及亮区域的暗点。既然两幅图像中 有相同的景物,那么使用某种方法分别提取各自的稳定点,这些点之间会有 相互对应的匹配点。
尺度空间(scale space )
尺度空间理论最早于1962年提出,其主要思想是通过 对原始图像进行尺度变换,获得图像多尺度下的空间表示。 从而实现边缘、角点检测和不同分辨率上的特征提取,以 满足特征点的尺度不变性。
尺度空间中各尺度图像的 模糊程度逐渐变大,能够模拟 人在距离目标由近到远时目标 在视网膜上的形成过程。 尺度越大图像越模糊。
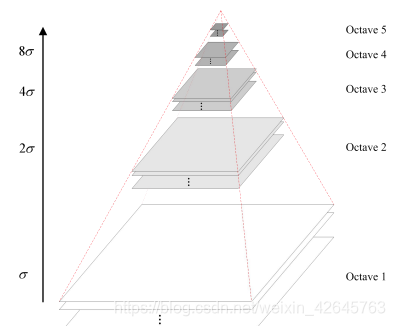
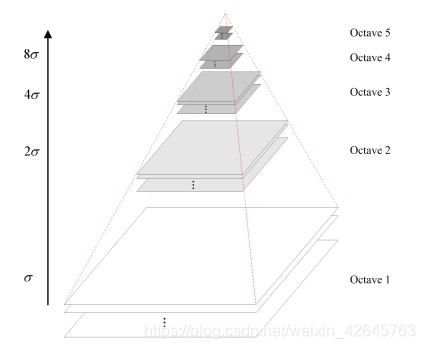
高斯金字塔
高斯金子塔的构建过程可分为两步:
(1)对图像做高斯平滑;
(2)对图像做降采样。
为了让尺度体现其连续性,在简单 下采样的基础上加上了高斯滤波。 一幅图像可以产生几组(octave) 图像,一组图像包括几层 (interval)图像。
高斯图像金字塔共o组、s层, 则有:
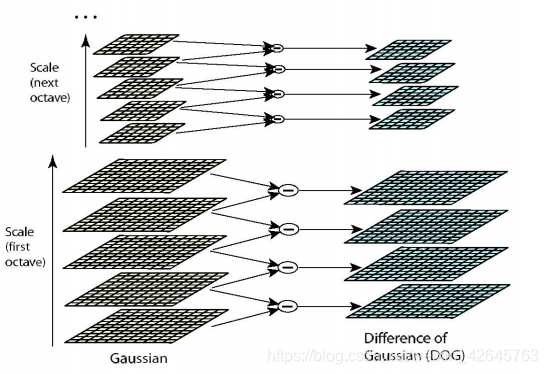
关键点检测——DOG
DoG高斯差分金字塔
对应DOG算子,需构建DOG金字塔
可以通过高斯差分图 像看出图像上的像素 值变化情况。(如果没有变化,也就没有特征。特征必须是变化尽可能多的点。)
DOG图像描绘的是目标的轮廓。

DOG局部极值检测
DoG的局部极值点
特征点是由DOG空间的局部极值点组成的。为了寻找DoG函数的极值点, 每一个像素点要和它所有的相邻点比较,看其是否比它的图像域和尺度域 的相邻点大或者小。
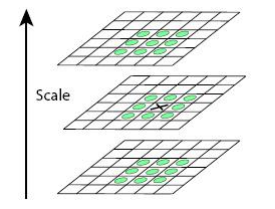
中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个 点共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点
去除边缘响应
由于DoG函数在图像边缘有较强的边缘响应,因此需要排除边缘响应。 DoG函数的峰值点在边缘方向有较大的主曲率,而在垂直边缘的方向有 较小的主曲率。主曲率可以通过计算在该点位置尺度的2×2的Hessian矩 阵得到,导数由采样点相邻差来估计
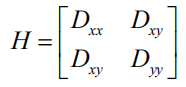
Dxx 表示DOG金字塔中某一尺度的图像x方向求导两次
D的主曲率和H的特征值成正比。令 α ,β为特征值,则
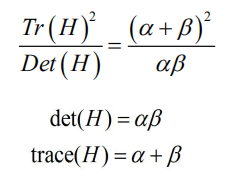
该值在两特征值相等时达最小。Lowe论文中建议阈值T为1.2,即
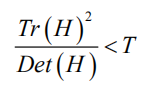
时保留关键点,反之剔除
关键点方向分配
通过尺度不变性求极值点,可以使其具有缩放不变的性质。而利 用关键点邻域像素的梯度方向分布特性,可以为每个关键点指定方向参数 方向,从而使描述子对图像旋转具有不变性。
通过求每个极值点的梯度来为极值点赋予方向。
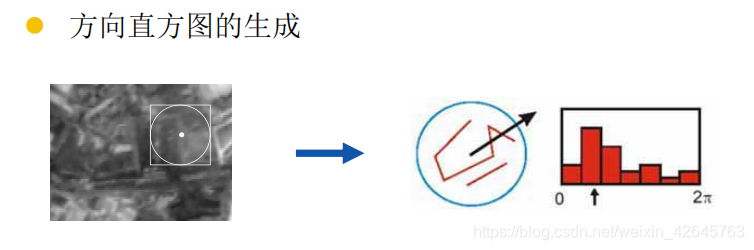
确定关键点的方向采用梯度直方图统计法,统计以关键点为原 点,一定区域内的图像像素点对关键点方向生成所作的贡献
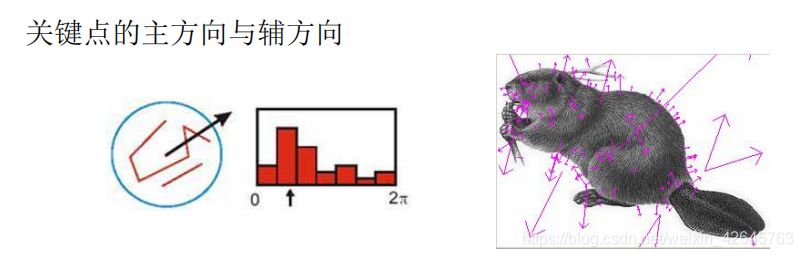
• 关键点主方向:极值点周围区域梯度直方图的主峰值也是特征点方向
• 关键点辅方向:在梯度方向直方图中,当存在另一个相当于主峰值 80%能量的峰值时,则将这个方向认为是该关键点的辅方向。
这可以增强匹配的鲁棒性,Lowe的论文指出大概有15%关键点具有 多方向,但这些点对匹配的稳定性至为关键。
关键点描述
下图是一个SIFT描述子事例。其中描述子由2×2×8维向量表征,也即是 2×2个8方向的方向直方图组成。左图的种子点由8×8单元组成。每一个小格 都代表了特征点邻域所在的尺度空间的一个像素,箭头方向代表了像素梯度方 向,箭头长度代表该像素的幅值。然后在4×4的窗口内计算8个方向的梯度方 向直方图。绘制每个梯度方向的累加可形成一个种子点,如右图所示:一个特 征点由4个种子点的信息所组成
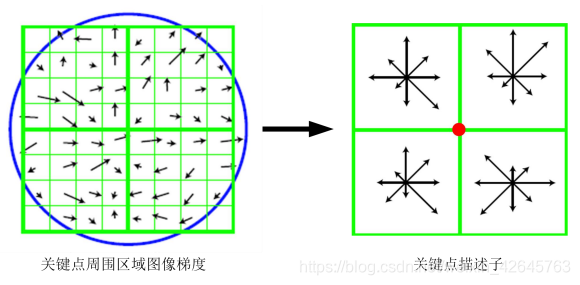
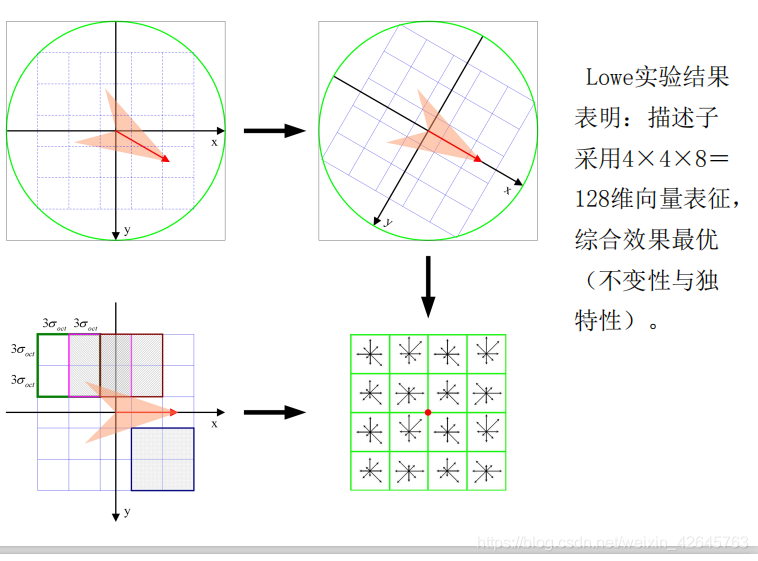
关键点匹配
分别对模板图(参考图,reference image)和实时图(观测图, observation image)建立关键点描述子集合。目标的识别是通过两点 集内关键点描述子的比对来完成。具有128维的关键点描述子的相似性度量采用欧式距离
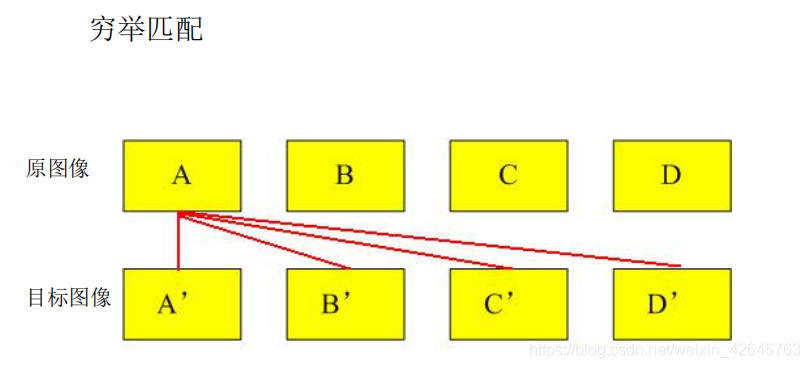

关键点的匹配可以采用穷举法来完成,但是这样耗费的时间太多,一般都采用kd树的数据结构来完成搜索。搜索的内容是以目标图像的关键点为基准,搜索与目标图像的特征点最邻近的原图像特征点和次邻近的原图像特征点。Kd树是一个平衡二叉树。
关键点匹配效果
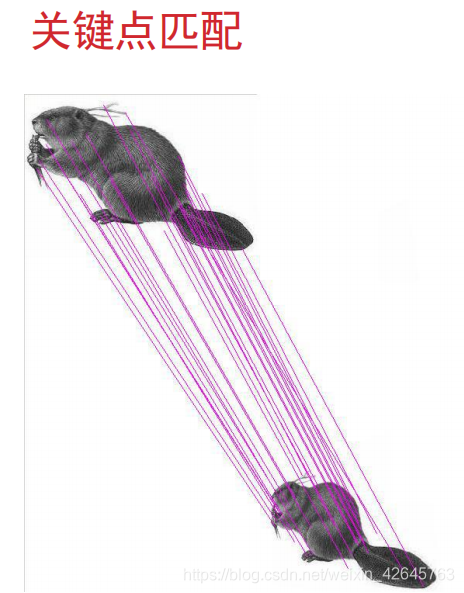
三、实验要求
(1)使用多张图片(注意要来自不同场景),构造出一个小的数据集。
(2)实现数据集中,每张图片的SIFT特征提取,并展示特征点
(3)给定两张图片,计算其SIFT特征匹配结果
(4)给定一张输入的图片,在数据集内部进行检索,输出与其匹配最多的三张图片
(5) 匹配地理标记
四、实验代码
1.特征点展示 sift1.py
2.描述子算法 sift2.py
3.检索匹配算法 sift3.py
4.局部描述子进行匹配 sift4.py
5.可视化连接图像 sift5.py
五、实验结果及分析
1.使用多张图片(注意要来自不同场景),构造出一个小的数据集。

2.特征点展示













分析:从实验结果可以看到,SIFT特征找到的特征点与Harris角点找出的特征点的位置有些不同。在一些场景下,Harris角点经常失效,而SIFT特征找到的特征点却都能找到。
3.给定两张图片,计算其SIFT特征匹配结果
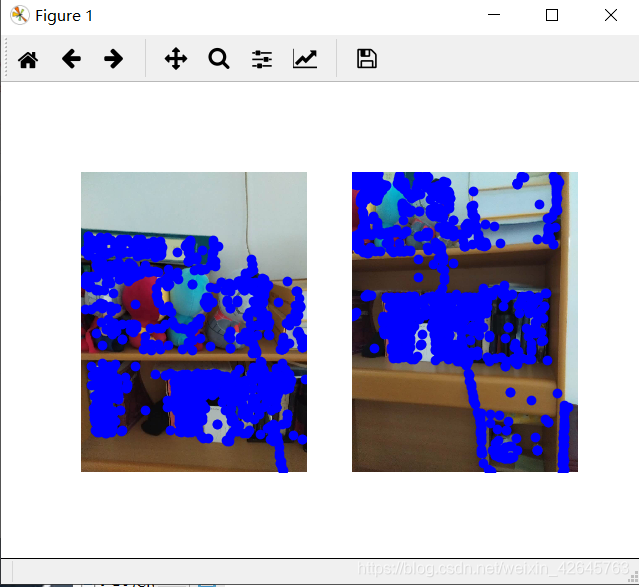
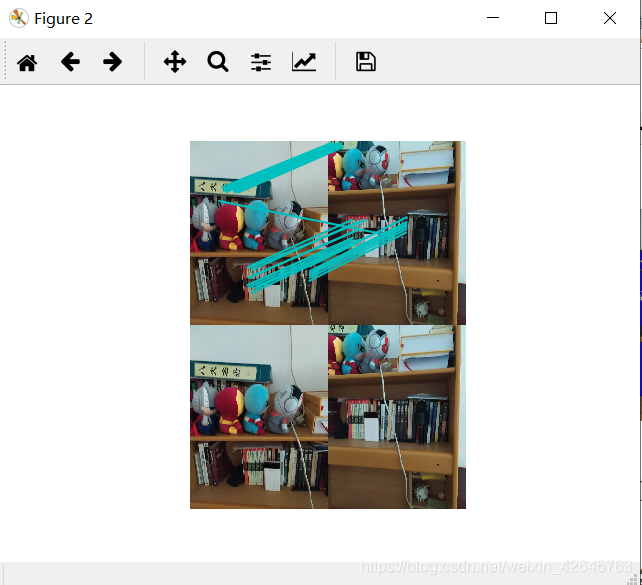


分析:因为SIFT算法具有尺度和旋转不变性,即使两张图大小不一样、角度不一致也不会影响匹配结果,而之前实验的Harris角点对尺度变化非常敏感,当遇到尺度变化较大时,很多正确特征点无法检测出来。
4.给定一张输入的图片,在数据集内部进行检索,输出与其匹配最多的三张图片
输入照片为


分析:SIFT算法很快的检索到了匹配度较高的图片,由此可以看出该算法的性能十分强大,对于旋转、尺度、缩放、亮度变化保持不变性,对于视角变化、远近距离也能保持原有的稳定性。适用于信息量大,复杂的环境。
4.地理标记图像匹配
数据集

首先在原有数据集上,提取局部描述子
通过图像间是否具有匹配的局部描述子来定义图像的连接,然后可视化这些连接情况

分析:实验结果如图所示,我分别选取不同角度,不同距离,不同方向的尚大楼作为数据集,体现了sift算法的尺度不变性和旋转不变性。而且在东大门拍摄的大楼从观感上来看,有点类似于尚大楼,但是该算法却没有将它认为是同一种类型,这表明sift算法的准确性非常精确。
六、总结
实验中出现的一些错误:
1.实验中出现“No such file or directory: ‘empire.sift’.这个应该是vlfeat安装版本不兼容的原因,下载旧版,0.9.20,里面有win64版本的,把vlfeat-0.9.20\bin 下面的sift.exe和vl.dll 拷到项目目录下。因为我用的是Anaconda软件,所以要修改一下PCV中cmmd的路径为cmmd = str(r"D:\pythonproject\sift.exe “+imagename+” --output="+resultname+" "+params)注意要加r,且sift.exe后面有空格,文件路径不要出现空格。
2.实验中出现only integers,slices(:)错误,提示数据类型错误,只需要把PCV目录下的sift.py文件中的pplot([locs1[i, 0],locs2[matchscores [i,0] ,0]+cols1],[locs1[i,1], locs2[matchscores[i,0],1]], ‘C’)改为plot([locs1[i,0],locs2[int(matchscores[i,0]),0]+cols1],[int(locs1[i,1]), locs2[int (matchscores[i,0]),1]1,‘c’),强制转换即可。
3.实验中出现ValueError: all the input arrays must have same number of dimensions错误,我做实验第一部分的时候用的是网上找的图,能找到特征点,但是特征点匹配的时候运行不了描述子算法,换成自己拍的照就可以,原因是网上找到的图,像素都不同,而该算法要求像素必须一致才能进行匹配,将图像转为灰度化也可解决。
SIFT(局部特征提取)算法的一些特性
1.SIFT算法是一种提取局部特征的算法,在尺度空间寻找极值点,提取位置,尺度,旋转不变量
2.SIFT特征是图像的局部特征,其对旋转、尺度缩放、亮度变化保持不变性,对视角变化、仿射变换、噪声也保持一定程度的稳定性。
3.独特性好,信息量丰富,适用于在海量特征数据库中进行快速、准确的匹配。
4.多量性,即使少数的几个物体也可以产生大量SIFT特征向量。
5.可扩展性,可以很方便的与其他形式的特征向量进行联合。







 已为社区贡献2条内容
已为社区贡献2条内容

所有评论(0)