系列文章目录

时空图神经网络1——GNN和GCN
时空图神经网络2——RNN和GRU
时序图神经网络3——T-GCN

---

---

一、前言

在实际生活中，很多对象可以被看作图结构，有时候他们的边有相似但却又不同的性质。比如交通网络中，每一条道路都可以被看作边，每条路的情况却不同：有的是单行道，有的是双车道，有的是四车道，显然会对节点有不同程度的影响。那我们如何考虑这种影响？
GATConv中包含了参数edge_attr，可以用来储存边的属性，我们一起来学习一下！

---

二、图注意力网络 GAT

我们之前讲过了图卷积网络GCN，图注意力网络(Graph Attention Networks, GAT)是在GCN基础上的一次改进，不再用静态的归一化系数而是通过自注意力计算的加权因子。具体来说，GCN中，邻居节点的影响是相同的，毕竟只考虑了节点的度；而在GAT中要考虑不同邻居节点的重要性。举个简单的例子：一个班有 50 个同学，相当于 50 个节点，但是只有几个同学对你的影响比较大，大多数影响不太大，还有一些近似于陌生人，说明你们之间的联系（边）很弱。

官方文档
参考文献

2.1 什么是注意力？

参考文献中的图注意力算子(graph attentional operator)定义如下：$${\tilde{x}}_i=\sum _{j\in {\mathcal{N}}_A}{\alpha }_{ij}W{x}_j$$其中 ${\alpha }_{ij}$ 是注意力系数(attention coefficients)，这部分的计算比较复杂，我们需要拆开来看。在这之前先提一个问题，自注意力又是什么呢？了解transformer的同学可能知道是什么意思，自注意力机制的核心大概可以概括为“相关性”，在图中，我们可以认为是节点之间的相关性。我们认为两个向量相乘得到的值比较大就是相关性大，两个向量相乘的值比较小就是相关性小。
举个例子即使一下，向量$a=[1,0]$，向量$b=[-1,0]$， 向量$c=[0,1]$，向量$d=[\sqrt{2},\sqrt{2}]$。在二维坐标系中，我们结合图片分析这几个向量：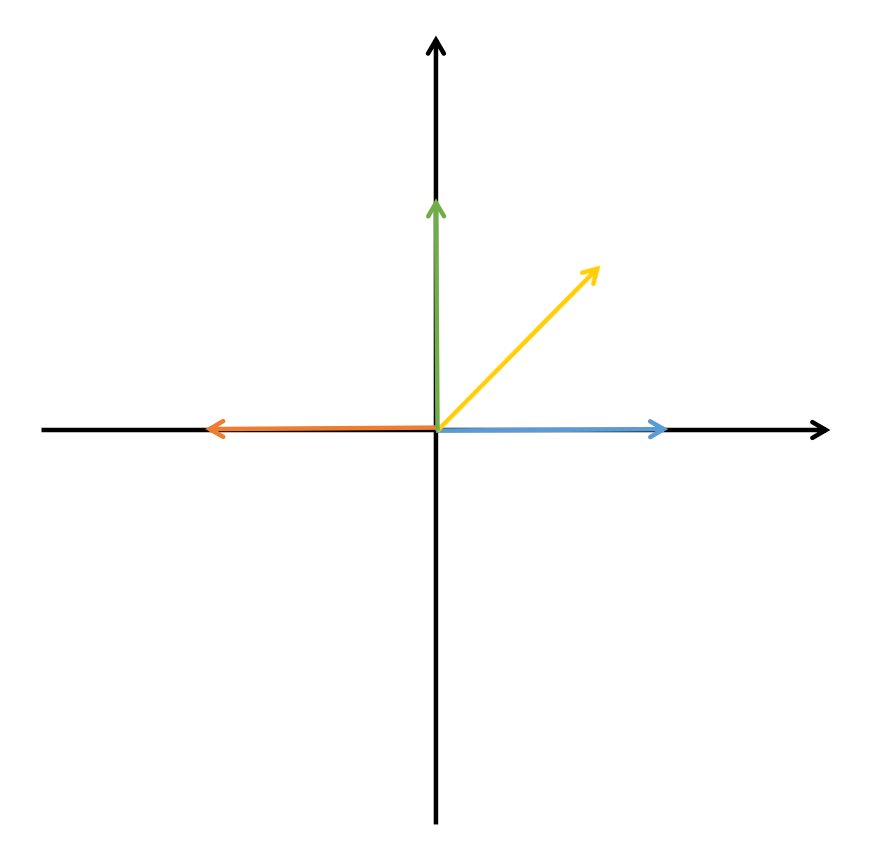

首先 $a$ 和自身是有关的，而且是最有关的，$a{a}^T=1$；
$a$ 和 $b$ 方向完全相反，很明显我们知道二者是负相关的，且$a{b}^T=-1$；
$a$ 和 $c$ 二者正交，也就是相互垂直，我们知道在数学中正交代表无关，且$a{c}^T=0$；
对于 $a$ 和 $d$ 来说，他们之间正相关，因为 $d$ 在横轴上有投影，但是它在纵轴也有投影，总的来说，$a{d}^T=\sqrt{2}$，所以 $a$ 和 $d$ 相关（可以用 $\sqrt{2}$ 描述），但是又不如 $a$ 与自己相关（可以用 $1$ 来描述）。可以看出，两个向量（矩阵）相乘得到的积就像一个“分数”，分数越高相关性越大，分数是 0 就没有相关性，分数是负的就有负相关性。我相信通过这个例子，大家应该能大概对相关性有个简单的认识。

2.2 如何计算图注意力系数？

那么，我们如何计算中心节点和邻居节点之间的相关性大小？在图注意力层中，首先使用一个共享矩阵$W$对节点特征进行变换，也就是$W{x}_i$和$W{x}_j$，然后再把二者拼接(concatenate)起来（也可以不拼接，加起来也行，实际上没什么区别，官网上写的就是加起来，GRU中也有类似的拼接或者加起来的过程），再通过一个矩阵${\mathbf{a}}^{\mathbf{T}}$进行一次变换后加了一个激活函数LeakyReLU（线性变换+激活函数属于是常规操作），得到一个实数，这个实数我们在一定程度上可以认为是注意力系数，表示如下：$$e_{ij}=LeakyReLU({\mathbf{a}}^{\mathbf{T}}[W{x}_i||W{x}_j])$$
为什么我说是一定程度上？因为这还不是最终结果。如果模型训练好了以后，现阶段的注意力系数肯定也是能反映出相关性的大小的，但是根据惯例，我们要对其进行归一化，通常使用softmax来实现。$${\alpha }_{ij}={\text{softmax}}_j(e_{ij})=\frac{\exp (e_{ij})}{{\sum }_{k\in {\mathcal{N}}_i}\exp (e_{ik})}$$这次我们真的得到了注意力系数，进一步我们可以得到 ${\tilde{x}}_i$。但是！但是目前的自注意力还不稳定，这是因为我们只计算了一次，权重矩阵是随机的，可能会出现问题。

2.3 多头注意力机制

为了让我们计算出来的注意力系数更稳定，我们引入多头注意力机制（multi-head attention）。“多头”注意力机制听起来很抽象，实际上可以理解为“多次”注意力。为了避免一次注意力的不稳定性，我们计算多次再综合考虑，就能大大改善效果。
只需要重复上述操作，每次都可以得到一个 ${\tilde{x}}_i^k$ ，通过平均法和连接法可以合并计算结果。
平均法按照注意力头的数量归一化：$${\tilde{x}}_i=\frac{1}{n}\sum _{k=1}^n{\tilde{x}}_i^k=\frac{1}{n}\sum _{k=1}^n\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{W}^k{x}_j$$
连接法将每个头的结果拼接起来得到更大的矩阵：$${\tilde{x}}_i={\Vert }_{k=1}^n{\tilde{x}}_i^k={\Vert }_{k=1}^n\sum _{j\in {\mathcal{N}}_i}{\alpha }_{ij}^k{W}^k{x}_j$$
到目前为止看起来一切都结束了，所有内容都讲完了。可是我们是为什么要讲GAT来着？我们是为了考虑边的影响！

2.4 边属性的使用

在GNN中，不同模型涉及到的入参不太一样。有的存在edge_weight这个入参，有的没有，但是有edge_attr这个入参。什么区别呢？顾名思义，edge_weight表示边权重，意思就是我们已经知道某个边对中心节点的影响程度，然后给边指定上这个权重。edge_weight是一个一维张量，与edge_index的顺序一一对应，比如下面这个例子：

edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)
edge_weight = torch.tensor([0.5, 1.0, 2.0, 0.3], dtype=torch.float)

edge_index是将我们之前提到过的尺寸为[num_nodes, num_nodes]的邻接矩阵变成尺寸为[2, num_edges]的矩阵（无向图是这样的）。因为在图很大但是连接又稀疏的情况下，邻接矩阵中大部分元素是 0，其实没有意义。邻接矩阵的尺寸过大会影响计算和存储效率，所以需要进行降维。我们可以看个例子，假设有一个邻接矩阵：

adj = [[0,1,1,0,0,0,0],
       [1,0,0,1,1,0,0],
       [1,0,0,0,0,1,1],
       [0,1,0,0,0,0,0],
       [0,1,0,0,0,0,0],
       [0,0,1,0,0,0,0],
       [0,0,1,0,0,0,0]]

改成edge_index的形式为：

edge_index = [(0, 1), (0, 2), (1, 3), (1, 4), (2, 5), (2, 6)]

明显简洁了很多。话又说回来，edge_attr与edge_weight的区别又在哪里？edge_weight 只存储单一的权重值，edge_attr 允许存储一个向量或多维数组，更通用的表达了边的属性特征，比如下面这个例子：

edge_index = torch.tensor([[0, 1, 1, 2],
                           [1, 0, 2, 1]], dtype=torch.long)
edge_attr = torch.tensor([[1, 2], [3, 4], [5, 6], [7, 8]], dtype=torch.float)

引入 edge_attr 的目的在于让模型在计算注意力系数时能考虑边的特征。在很多实际场景中，边的特征（例如边的权重、类型等）能够为图的结构和节点间的关系提供额外的信息。借助将边的特征纳入注意力系数的计算，模型能够更精准地捕捉节点间的关联，从而提升模型的表达能力和性能。想知道哪些支持edge_weight 和 edge_attr 可以从GNN Cheatsheet中查看。那么在GAT中，edge_attr是如何被使用的呢？
跟节点一样。其实很好理解，对于某个几点来说，有几个邻居节点就有几个边，对边同样进行相同的注意力机制的运算，并且一起拼接或者求和即可。我们看一下官网上的公式就可以知道了，官网上用的不是拼接而是求和，但是没什么区别，一样的。

上面的式子表示没有edge_attr的情况，下面有了就一起进行相同处理即可！

2.5 GATv2Conv

GATv2Conv是改进的GAT，区别在于注意力权重矩阵在激活函数后面使用。直接看官网的式子，可以跟GAT的对比。

其他没区别，但是GATv2的性能使用优于GAT，所以应该优先选择GATv2。

2.6 参数介绍

以GATConv为例，我们可以直接导入：

from torch_geometric.nn.conv import GATConv

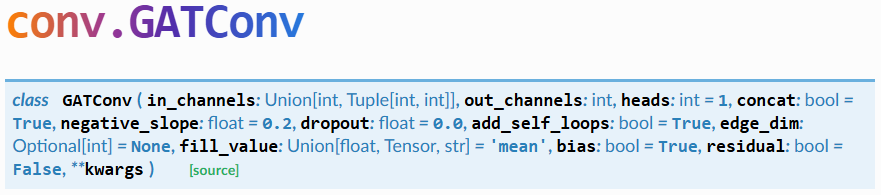
参数：

• in_channels（int 或 tuple）：每个输入样本的大小，如果设置为 -1，则会从 forward 方法的第一个输入中推导其大小。在二分图的情况下，元组对应源节点和目标节点的维度大小。
• out_channels（int）：每个输出样本的大小。
• heads（int，可选）：多头注意力的数量。（默认值：1，我觉得应该多写几个，要不然没意义了）
• concat（bool，可选）：如果设置为 False，多头注意力的结果将被平均而不是拼接。（默认值：True）
• negative_slope（float，可选）：LeakyReLU 负斜率的角度。（默认值：0.2）
• dropout（float，可选）：归一化注意力系数的随机失活概率，在训练期间使每个节点随机采样邻居节点。（默认值：0）
• add_self_loops（bool，可选）：如果设置为 False，则不会向输入图添加自环。（默认值：True）
• edge_dim（int，可选）：边特征的维度（如果存在的话）。（默认值：None）
• fill_value（float 或 torch.Tensor 或 str，可选）：生成自环边特征的方式（在 edge_dim != None 的情况下）。如果是 float 或 torch.Tensor，自环的边特征将直接由 fill_value 给出。如果是 str，自环的边特征将根据指定的规约操作，通过聚合指向特定节点的所有边的特征来计算（取值为 “add”、“mean”、“min”、“max”、“mul”）。（默认值：“mean”）
• bias（bool，可选）：如果设置为 False，该层将不学习加性偏差。（默认值：True）
• residual（bool，可选）：如果设置为 True，该层将添加一个可学习的跳跃连接。（默认值：False）
• **kwargs（可选）：conv.MessagePassing 的其他参数。
  形状：
• 输入：节点特征为(|V|, F_in) 或二分图时为 ((|V_s|, F_s), (|V_t|, F_t))(二分图先不管)；边索引为 (2, |E|)；边特征为 (|E|, D)（可选）。
• 输出：节点特征为 (|V|, H*F_out) 或二分图时为 (|V_t|, H * F_out)。如果 return_attention_weights=True，则输出为 ((|V|, H*F_out), ((2, |E|), (|E|, H))) 或二分图时为 ((|V_t|, H*F_out), ((2, |E|), (|E|, H)))。

总结

本文介绍了图注意力网络的架构，主要目的是为了在图中考虑边属性的影响。