工作中遇到某个场景看起来可以用时序图神经网络来解决，本系列文章用来记笔记，顺便分享。
参考文献：

SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL ETWORKS

参考博客：

图神经网络实战（7）——图卷积网络(Graph Convolutional Network, GCN)详解与实现
图卷积网络(Graph Convolutional Networks, GCN)详细介绍

---

---

前言

学习时序图神经网络需要对图神经网络有基本的认识，首先从最简单的GNN和GCN开始讲起。
本文在理解原文的基础上，参考了其他博主的blog，整理出来作为笔记，既给自己看，也分享给大家。

---

一、GNN

1 GNN简介

图神经网络(Graph Neural Network, GNN)是一种专门用于处理图数据的深度学习模型。传统的神经网络主要用于处理向量或序列数据，而图神经网络则可以有效地处理非结构化的图形数据，如社交网络、推荐系统中的用户-物品关系、生物信息学中的蛋白质相互作用网络等。
图神经网络通过学习节点之间的连接模式和拓扑结构来捕捉图数据中的信息传播和相互作用。它通过将每个节点及其邻居节点的特征进行聚合和更新，从而实现对整个图的表示学习。在图神经网络中，通常会定义节点表示(node embedding)和边表示(edpe embedding)，以便更好地表示节点之间的关系和特征。
图神经网络的基本原理是通过多层神经网络结构来逐步传播和更新节点的特征信息，从而实现对整个图的全局信息的学习和表示。这种方式可以帮助图神经网络在保留局部结构信息的同时，也考虑了全局图的拓扑结构和特征之间的关系，从而提高了对图数据的建模能力。图神经网络已经在许多领域得到广泛应用，包括社交网络分析、推荐系统、生物信息学、知识图谱Q等。它为处理复杂的非结构化数据提供了一种强大的工具，有助于挖掘数据中的潜在模式和关联，从而推动了深度学习在图数据分析领域的发展和应用。

2 GNN基本原理

先考虑普通的神经网络，当通过一个线性层进行线性变换时，$h_A=x_A{W}^T$，代表对向量，其中$x_A$是输入向量，$W$是线性层的权重矩阵。

对于图神经网络，需要聚合周围邻居的特征，因此经过的图线性层可表示为$h_A={\sum }_{i\in {\mathcal{N}}_A}{x}_i{W}^T$，其中${\mathcal{N}}_A$表示为节点$A$的邻居集，节点$A$聚合了所有邻居节点的信息。也就是说，节点$A$的所有邻居进行线性变换后求和，得到了节点A的信息。（再加上自己的线性变换就考虑到了所有邻居和自身的信息）

经过一次图卷积层以后，节点$A$聚合了邻居节点的信息，与此同时，邻居节点也聚合了各自邻居节点的信息，当经过第二次图卷积层后，$A$节点就可以得到”邻居的邻居“的信息。

这里有一个问题，邻居节点的数量可能会很多，每个邻居节点都有自己的权重矩阵$W$会导致计算量过大，因此邻居节点共享矩阵，即$H=X{W}^T$，其中$X$是输入，尺寸为[num_nodes, num_features]。然而这样看起来好像聚合了所有节点的信息。因此再引入邻接矩阵$A$，考虑节点之间的连接，即$H=AX{W}^T$。如果要考虑中心节点，就要对$A$进行处理：$A=A+I$，表示自己与自己相连。

举个例子，Cora数据集是一个由2708 篇机器学习领域科学论文构成的引文网络，论文间通过5429 条引用关系相互连接，形成有向图。论文被划分为7类，常用图图神经网络的分类任务。数据展示如下：

        0    1    2    3    4    5  ...  1428  1429  1430  1431  1432  label
0     0.0  0.0  0.0  0.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      3
1     0.0  0.0  0.0  0.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      4
2     0.0  0.0  0.0  0.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      4
3     0.0  0.0  0.0  0.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      0
4     0.0  0.0  0.0  1.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      3
...   ...  ...  ...  ...  ...  ...  ...   ...   ...   ...   ...   ...    ...
2703  0.0  0.0  0.0  0.0  0.0  1.0  ...   0.0   0.0   0.0   0.0   0.0      3
2704  0.0  0.0  1.0  0.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      3
2705  0.0  0.0  0.0  0.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      3
2706  0.0  0.0  0.0  0.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      3
2707  0.0  0.0  0.0  0.0  0.0  0.0  ...   0.0   0.0   0.0   0.0   0.0      3

[2708 rows x 1434 columns]

数据集主要包含两个文件：

• content文件：记录论文（节点）的详细信息。每行表示一篇论文，格式为 [论文ID, 词向量, 类别标签]。其中，词向量是由1433个唯一单词构成的二进制向量（1 表示单词存在，0 表示不存在），因此特征维度为 1433。
• cites文件：记录论文间的引用关系（边）。每行包含两个论文 ID，格式为 [被引用论文ID, 引用论文ID]，表示有向边。

分析数据的情况可以得知，每篇论文都是一个节点，每一行都代表一篇论文中的词向量，也就是说除了label列的每一列都是一个特征。所以GNN的输入结构就是[2708, 1433]，对应[num_nodes, num_features]。

注意： 在这种简单的GNN中，经过线性变换以后，改变的只是特征数，节点数保持不变。如经过两次变换后与label对比，尺寸变化从[num_nodes, num_features]->[num_nodes, num_hidden_features]->[num_nodes, dim_out]

3 一个例子

来源：图卷积网络(Graph Convolutional Networks, GCN)详细介绍
如下图所示，对于给定的无向网络：$G=(V,E)$
其中$V$包含网络中所有的$N$个节点，$v_i\in V$，$E$代表节点之间的边，$(v_i,v_j)\in V$。
$A$是$N\times N$的邻接矩阵，$A_{i,j}$代表节点$i$和节点$j$之间的连接状态。$A_{i,j}=1$表示有连接，$A_{i,j}=0$表示无连接。或者$A_{i,j}>0$表示有权重的连接，$A_{i,j}=0$表示无连接。
结点的特征向量矩阵为$X$，为$N\times C$的矩阵，其中$C$为特征数。

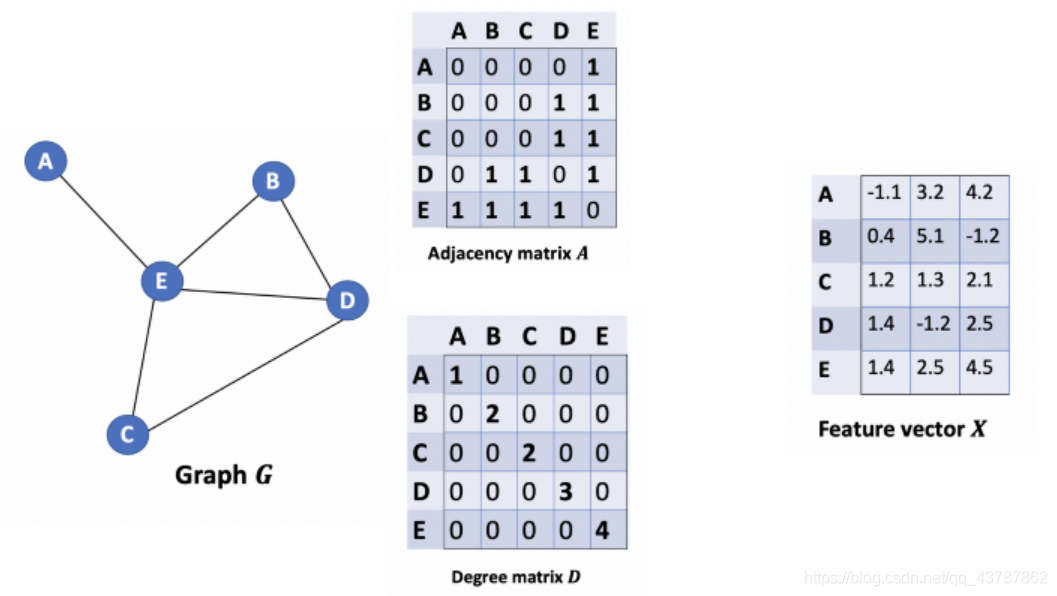
通过邻接矩阵与特征矩阵相乘，可以得到邻居节点的信息，如下图所示：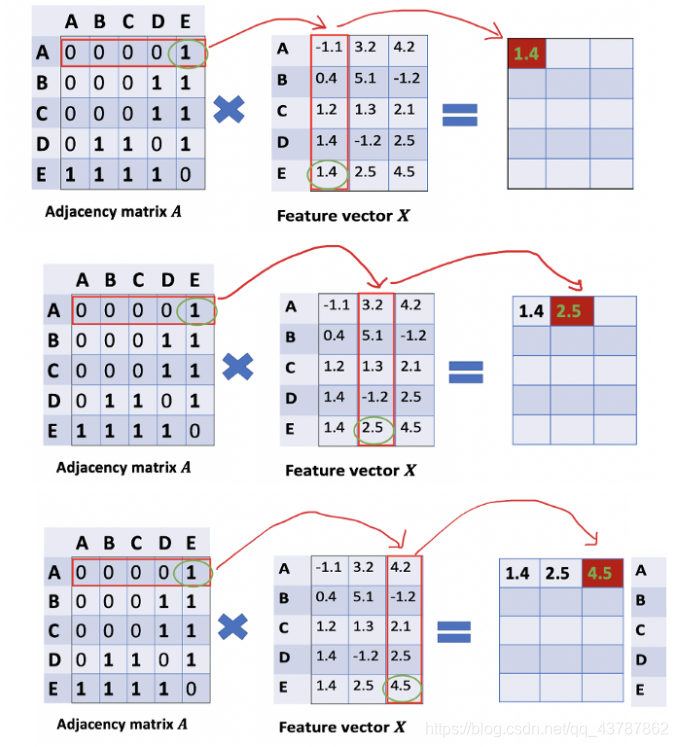

首先让我们看邻接矩阵的第一行，可以看到结点$A$连接着结点$E$。而结果矩阵中的第一行其实就是结点E的特征向量。类似地，结果矩阵中的第二行就是界定$D$与结点$E$的加和。通过这样一种处理，我们可以得到结点所有邻居的特征加和向量。
但是现在并没有考虑节点本省，像前文中说过的，加上一个对角线矩阵$I$，再进行同样的运算就可以了。

二、 GCN

1 GCN简介

GCN是图卷积网络，可以捕捉图网络的结构特征，已经成为最受欢迎的图神经网络之一，是处理图数据时创建基线模型的首选架构。
GCN可以直接通过torch_geometric调用：

from torch_geometric.nn import GCNConv

2 GCN 基本原理

GCN的原文写的相当复杂，我参考了两篇blog写在本文开头，都讲的很清楚：
在上面的GNN部分中，我们已经可以聚合节点自身和周围节点从而实现消息的传递和聚合。但是图数据中节点的邻居个数不总是相同的。
假设节点 1 有 1,808 个邻居，而节点 2 只有 1个邻居，那么 $h_1$的值将远远大于$h_2$的值。这样便会出现一个问题，当我们进行比较时，如果它们的值相差过大，如何进行有意义的比较？一个简单的解决方案是将嵌入除以邻居数量，用 $deg(A)$表示节点的度，因此 GNN 层公式可以更新为：
$$H=\frac{1}{\mathrm{deg}(A)}X{W}^T$$
具体解释如下：
首先回顾GNN层的计算公式$$H={\tilde{A}}^{T}X{W}^T$$其中，$\tilde{A}=A+I$，公式中缺少提供归一化系数矩阵$\frac{1}{\mathrm{deg}(A)}$。
我们可以先用度矩阵$D$来计算每个节点上邻居的数量。
根据定义，$D$给出每个节点的度$\mathrm{deg}(i)$。因此，根据矩阵的逆矩阵$D^{-1}$可以得到归一化系数$\frac{1}{\mathrm{deg}(A)}$。
为了更加精确，需要考虑自身的影响（添加自循环），用$\tilde{A}=A+I$表示，同样在度$D$矩阵中也加入自循环，$\tilde{D}=D+I$，最终归一化矩阵为${\tilde{D}}^{-1}={(D+I)}^{-1}$。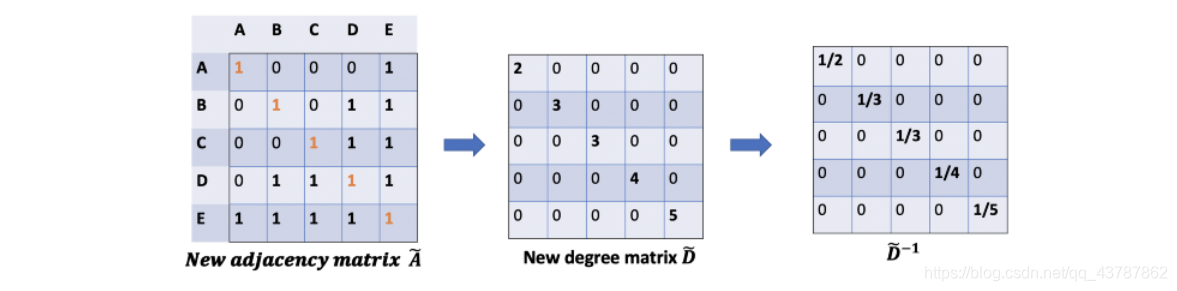

得到了这个归一化矩阵，我们如何使用呢？
如果进行${\tilde{D}}^{-1}\tilde{A}X{W}^T$操作，会对行特征归一化
如果进行$\tilde{A}{\tilde{D}}^{-1}X{W}^T$从中，会对列进行归一化
在第一种情况下，每一行的和都等于1；在第二种情况下，每一列的和都等于1。在论文中，作者使用一种混合归一化来解决这个问题，$${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X{W}^T$$文章中表示为$$H^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right).$$其中，$\sigma$是激活函数。
这就是原始的图卷积层的数学公式，与GNN一样，可以通过堆叠图卷积层创建GCN网络。GCN的输入$X$与GNN中相同，也是[num_nodes, num_features]，有时num_features也被称作特征图个数。

3 GNN的网络层数

网络的层数代表着结点特征所能到达的最远距离。
在前文也已经提过，经过一层GNN或者GCN，可以得到节点A邻居节点的信息。但是再远一点的节点信息你是得不到的，需要在第二个GCN层才能得到，因为此时节点A的邻居节点已经聚合了邻居节点的邻居节点的信息。
也就是说，一层的GCN，每个结点只能得到其一阶邻居身上的信息。对于所有结点来说，信息获取的过程是独立、同时开展的。当我们在一层GCN上再堆一层时，就可以重复收集邻居信息的过程，并且收集到的邻居信息中已经包含了这些邻居结点在上一个阶段所收集的他们的邻居结点的信息。这就使得GCN的网络层数也就是每个结点的信息所能达到的maximum number of hops。因此，我们所设定的层的数目取决于我们想要使得结点的信息在网络中传递多远的距离。需要注意的是，通常我们不会需要结点的信息传播太远。经过6~7个hops，基本上就可以使结点的信息传播到整个网络，这也使得聚合不那么有意义。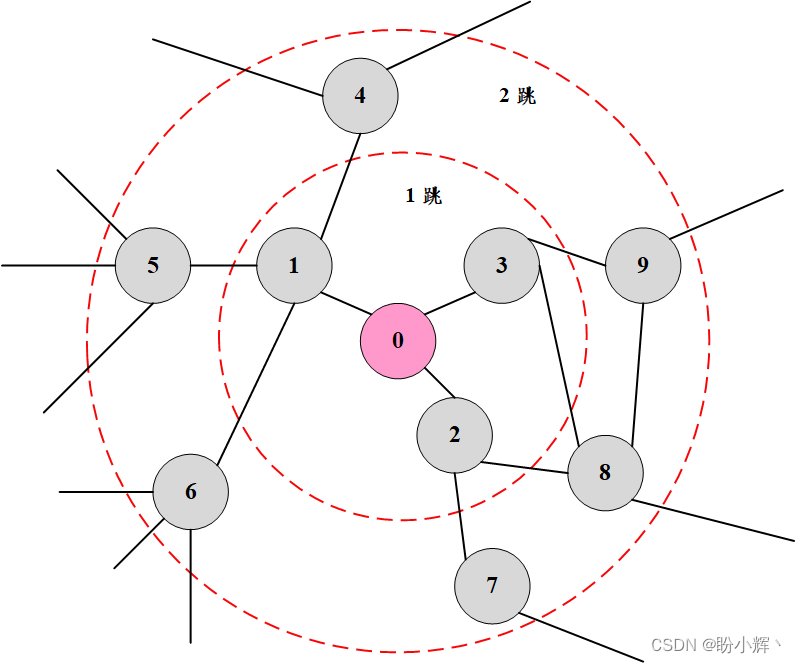

在文章中，作者对于深层GCNs和浅层GCNs的效果开展了一些实验，由图可以看到，2~3层的网络应该是比较好的。当GCN达到7层时，效果已经变得较差，但是通过加上residual connections between hidden layers可以使效果变好。下图可以给我们选择GCN层数提供参考。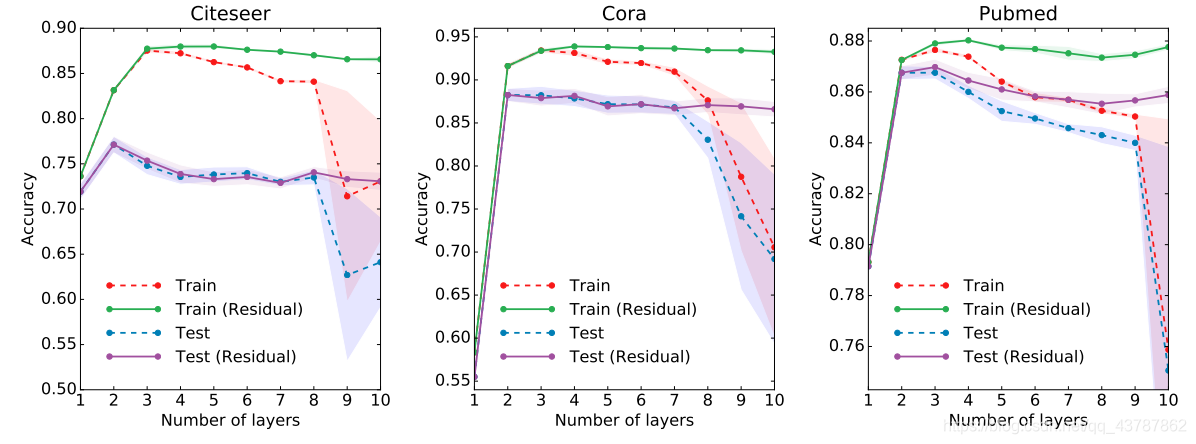

总结

• 介绍了GNN如何通过连接传递邻居节点信息
• 介绍了GCN如何消除邻居节点个数不同，造成线性变换后各节点特征值性差过大的问题
• 讨论了GCN层数的效果