MXNet卷积神经网络对图像边缘的检测

MXNet中的卷积层，以及对感受野的熟悉

寅恪光潜

794人浏览 · 2022-05-23 11:51:52

寅恪光潜 · 2022-05-23 11:51:52 发布

卷积神经网络是近年来在计算机视觉领域取得突破性成果的基石，在其他领域也有着广泛使用，前面也有很多相关的文章，有兴趣的可以参看：

卷积神经网络（CNN）相关的基础知识

卷积神经网络（CNN）结尾篇：可视化跟踪（Visualize）

卷积神经网络（CNN）之卷积层的实现

这节主要是在MXNet框架下，卷积层是如何进行图像特征提取的，基础的互相关运算如下：

from mxnet import autograd,nd
from mxnet.gluon import nn

#互相关运算，实质就是加权和，在d2lzh包中有定义
def corr2d(X,K):
    h,w=K.shape
    Y=nd.zeros((X.shape[0]-h+1,X.shape[1]-w+1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i,j]=(X[i:i+h,j:j+w]*K).sum()
    return Y
X=nd.arange(9).reshape(3,3)
K=nd.arange(4).reshape(2,2)
print(corr2d(X,K))

'''
[[19. 25.]
 [37. 43.]]
<NDArray 2x2 @cpu(0)>
'''

假设图像是高宽分别为6像素和8像素的黑白照片（0为黑色，1为白色），我们将会看到输出，在相邻变化的位置有了变化

垂直方向的边缘检测

X=nd.ones((6,8))
X[:,2:6]=0 #第二列到第三列所有行，赋值为0
K=nd.array([[2,-2]]) #1x2的卷积核
Y=corr2d(X,K)

'''
[[1. 1. 0. 0. 0. 0. 1. 1.]
 [1. 1. 0. 0. 0. 0. 1. 1.]
 [1. 1. 0. 0. 0. 0. 1. 1.]
 [1. 1. 0. 0. 0. 0. 1. 1.]
 [1. 1. 0. 0. 0. 0. 1. 1.]
 [1. 1. 0. 0. 0. 0. 1. 1.]]
<NDArray 6x8 @cpu(0)> 
[[ 0.  2.  0.  0.  0. -2.  0.]
 [ 0.  2.  0.  0.  0. -2.  0.]
 [ 0.  2.  0.  0.  0. -2.  0.]
 [ 0.  2.  0.  0.  0. -2.  0.]
 [ 0.  2.  0.  0.  0. -2.  0.]
 [ 0.  2.  0.  0.  0. -2.  0.]]
<NDArray 6x7 @cpu(0)>
'''

水平方向的边缘检测

X=nd.ones((6,8))
X[2:4,:]=0
K=nd.array([[2],[-2]])
Y=corr2d(X,K)
print(X,Y)

'''
[[1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]]
<NDArray 6x8 @cpu(0)> 
[[ 0.  0.  0.  0.  0.  0.  0.  0.]
 [ 2.  2.  2.  2.  2.  2.  2.  2.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]
 [-2. -2. -2. -2. -2. -2. -2. -2.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.]]
<NDArray 5x8 @cpu(0)>
<NDArray 5x8 @cpu(0)>
'''

对角线的边缘检测

X=nd.eye(5)
K=nd.array([[2,-2],[2,-2]])
Y=corr2d(X,K)
print(X,Y)

'''
[[1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 1.]]
<NDArray 5x5 @cpu(0)> 
[[ 0.  2.  0.  0.]
 [-2.  0.  2.  0.]
 [ 0. -2.  0.  2.]
 [ 0.  0. -2.  0.]]
<NDArray 4x4 @cpu(0)>
'''

我们使用框架自带的卷积层来验证下这个权重参数的结果：

conv2d=nn.Conv2D(1,kernel_size=(1,2))
conv2d.initialize()
X=X.reshape((1,1,6,8))#批量样本数、通道数、高、宽
Y=Y.reshape((1,1,6,7))
for i in range(10):
    with autograd.record():
        Y_hat=conv2d(X)
        l=(Y_hat-Y)**2#平方误差
    l.backward()
    conv2d.weight.data()[:]-=3e-2 * conv2d.weight.grad()
    if (i+1)%2==0:
        print('batch %d,loss %.3f'% (i+1,l.sum().asscalar()))
print(conv2d.weight.data().reshape((1,2)))

'''
batch 2,loss 20.054
batch 4,loss 3.374
batch 6,loss 0.570
batch 8,loss 0.097
batch 10,loss 0.017

[[ 1.9801984 -1.9732728]]
<NDArray 1x2 @cpu(0)>
'''
可以看到跟[[2,-2]]是非常接近的。

#使用lena图片来简单测试下：
from matplotlib.image import imread
import matplotlib.pyplot as plt

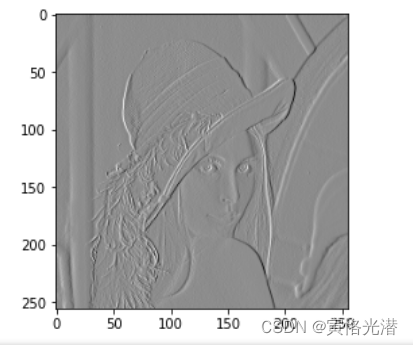
img=imread('lena.png')#256*256像素
X=nd.array(img)
K=nd.array([[1,-1]])
Y=corr2d(X,K)
plt.imshow(Y.asnumpy(),cmap=plt.cm.gray_r)
#这都可以检测到边缘，有点不可思议

自定义一个卷积层

使用前面的方法，继承Block，更多详情可以参看：MXNet自定义层（模型可携带参数）

class MyConv2D(nn.Block):
    def __init__(self,kernel_size,**kwargs):
        super(MyConv2D,self).__init__(**kwargs)
        self.weight=self.params.get('weight',shape=kernel_size)
        self.bias=self.params.get('bias',shape=(1,))
    
    def forward(self,x):
        return corr2d(x,self.weight.data())+self.bias.data()

conv2d=MyConv2D(kernel_size=(1,2))

不过使用corr2d这种方法会失败，不能反向传播求导，形状的原因，使用nd.Convolution，大家看它的定义其实可以发现，1D2D3D都有定义，1D少了height高度，3D多了depth深度，常用的是2D矩阵形式，修改如下：

class MyConv2D(nn.Block):
    def __init__(self,kernel_size,**kwargs):
        super(MyConv2D,self).__init__(**kwargs)
        self.weight=self.params.get('weight',shape=kernel_size)
        self.bias=self.params.get('bias',shape=(1,))
    
    def forward(self,x):
        '''
        - **data**: *(batch_size, channel, height, width)*
        - **weight**: *(num_filter, channel, kernel[0], kernel[1])*
        - **bias**: *(num_filter,)*
        - **out**: *(batch_size, num_filter, out_height, out_width)*.
        '''
        x=x.reshape((1,1,)+x.shape)
        w=self.weight.data()
        w=w.reshape((1,1,)+w.shape)
        return nd.Convolution(data=x,weight=w,bias=self.bias.data(),kernel=self.weight.shape,num_filter=1)

X=nd.ones((6,8))
X[:,2:6]=0
K=nd.array([[1,-1]])
Y=corr2d(X,K)

conv2d=MyConv2D(kernel_size=(1,2))
conv2d.initialize()
for i in range(10):
    with autograd.record():
        Y_hat=conv2d(X)
        l=(Y_hat-Y)**2#平方误差
    l.backward()
    conv2d.weight.data()[:]-=3e-2 * conv2d.weight.grad()
    if (i+1)%2==0:
            print('batch %d,loss %.3f'% (i+1,l.sum().asscalar()))
print(conv2d.weight.data().reshape((1,2)))


'''
batch 2,loss 4.622
batch 4,loss 0.782
batch 6,loss 0.137
batch 8,loss 0.029
batch 10,loss 0.011

[[ 0.9776625 -0.9999956]]
<NDArray 1x2 @cpu(0)>
'''

感受野(Receptive Field)

感受野是特征图上的一点映射到原始图像受影响的区域大小，换句话来说就是，输出的某点，一直回溯到输入，有多少个影响点。
画张图来更直观的了解下，也可以看出随着层的加深，感受野在加大（甚至可能大于输入的实际大小）

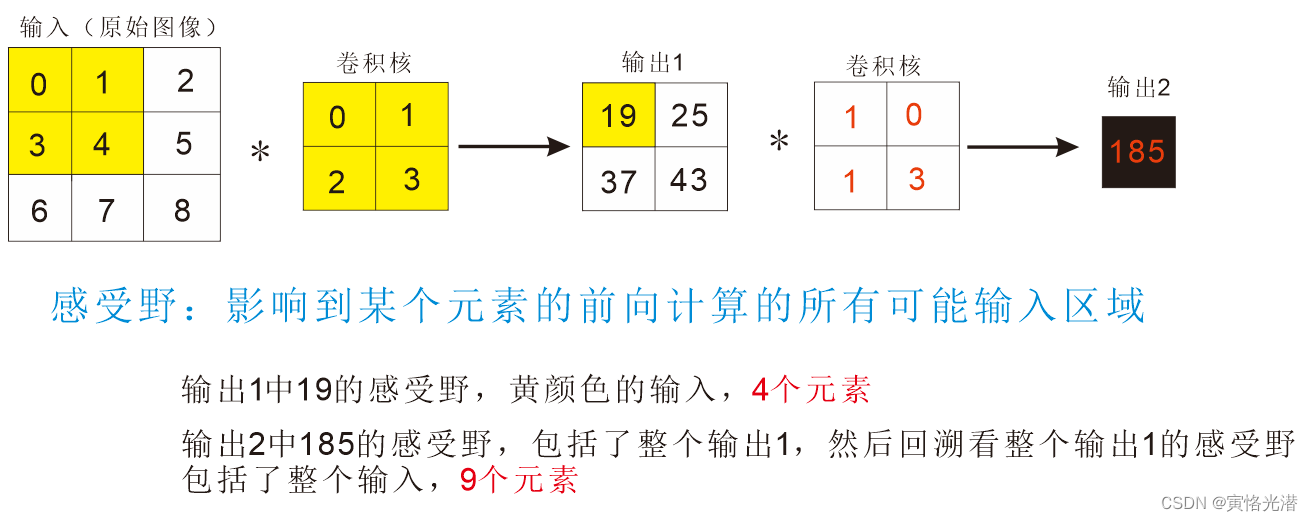
X=nd.arange(9).reshape(3,3)
K=nd.arange(4).reshape(2,2)
print(corr2d(X,K))
K1=nd.array([[1,0],[1,3]])
print(corr2d(corr2d(X,K),K1))
'''
[[19. 25.]
 [37. 43.]]
<NDArray 2x2 @cpu(0)>

[[185.]]
<NDArray 1x1 @cpu(0)>
'''