一、什么是k近邻？

k 近邻算法是一种简单且经典的监督学习算法，既可用于分类问题，也可用于回归问题。其核心思想是：对于一个待预测的样本，找到训练数据中与它 “距离最近” 的 k 个邻居，根据这 k 个邻居的类别（分类任务）或数值（回归任务）来决定该样本的预测结果。

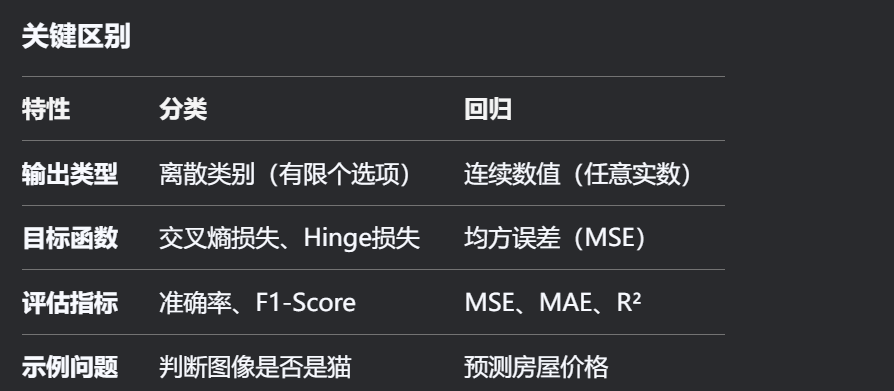
如何选择？

• 需要预测类别 → 分类（如用户是否会购买产品）。

• 需要预测数值 → 回归（如用户购买产品的金额）。

关键步骤：

1. 计算距离：常用欧几里得距离（连续数据）、曼哈顿距离、余弦相似度（文本 / 向量）等衡量样本间的相似性。
2. 选择 k 个最近邻居：根据距离排序，选取最近的 k 个样本。
3. 决策规则：
   1. 分类任务：通过 “多数投票”，选择 k 个邻居中出现最多的类别作为预测结果。
   2. 回归任务：计算 k 个邻居数值的平均值作为预测结果。

二、k 近邻的应用场景

1. 图像识别与分类

• 手写数字识别（如 MNIST 数据集）：通过计算像素特征的距离，识别手写数字。
• 人脸识别：判断待识别图像与已知人脸图像的相似性。

2. 推荐系统

• 基于用户行为的推荐：根据用户的历史行为（如浏览、购买记录），找到相似用户（k 个近邻），推荐他们喜欢的商品或内容（协同过滤的核心思想之一）。

3. 文本分类与自然语言处理

• 垃圾邮件分类：将邮件文本转换为特征向量（如词频向量），通过距离判断是否为垃圾邮件。
• 情感分析：根据文本的语义特征，参考相似文本的情感标签进行分类。

4. 生物信息学与医学

• 基因表达数据分类：通过基因表达特征区分癌症类型（如肿瘤与正常细胞）。
• 疾病诊断：根据患者的症状、病史等特征，参考相似病例的诊断结果。

5. 金融与信用评估

• 信用评分：通过用户的收入、借贷记录等特征，参考相似用户的信用等级，评估违约风险。

6. 异常检测

• 识别数据中与 k 个近邻差异较大的样本，判断是否为异常值（如信用卡欺诈交易检测）。

7. 实时预测

• 由于 k-NN 无需训练过程（直接存储训练数据），适合需要快速响应的场景，如实时个性化推荐。

三、k近邻原图理解

• X：代表训练样本，每一个养本有两个特征
• y：代表每一个样本的标签

1、数据准备

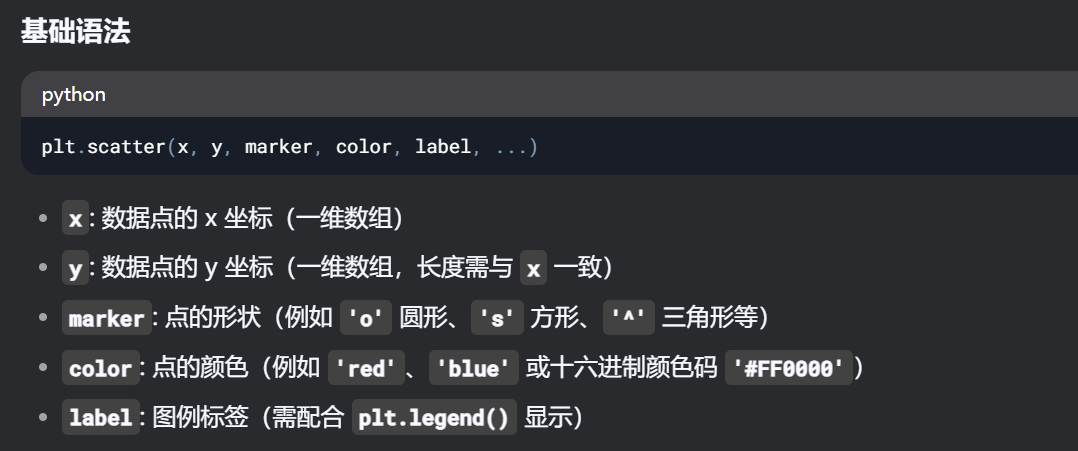
• plt.scatter 是 Matplotlib 库中用于绘制散点图（Scatter Plot）的函数

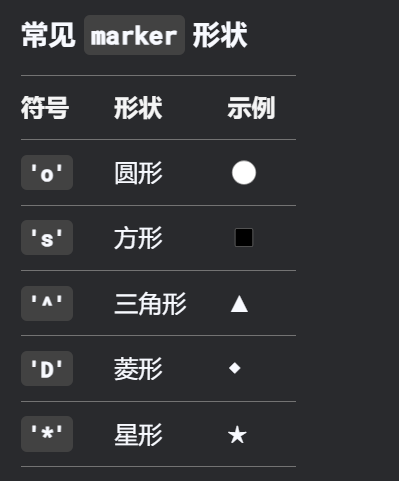
• X[条件, 列] 是 NumPy 的高级索引语法：

  • 条件：布尔数组，用来筛选行（样本）

  • 列：整数或切片，用来选择列（特征）

• X[y == 0, 0] = 标签为0的样本的第一个特征（x坐标）

• X[y == 0, 1] = 标签为0的样本的第二个特征（y坐标）

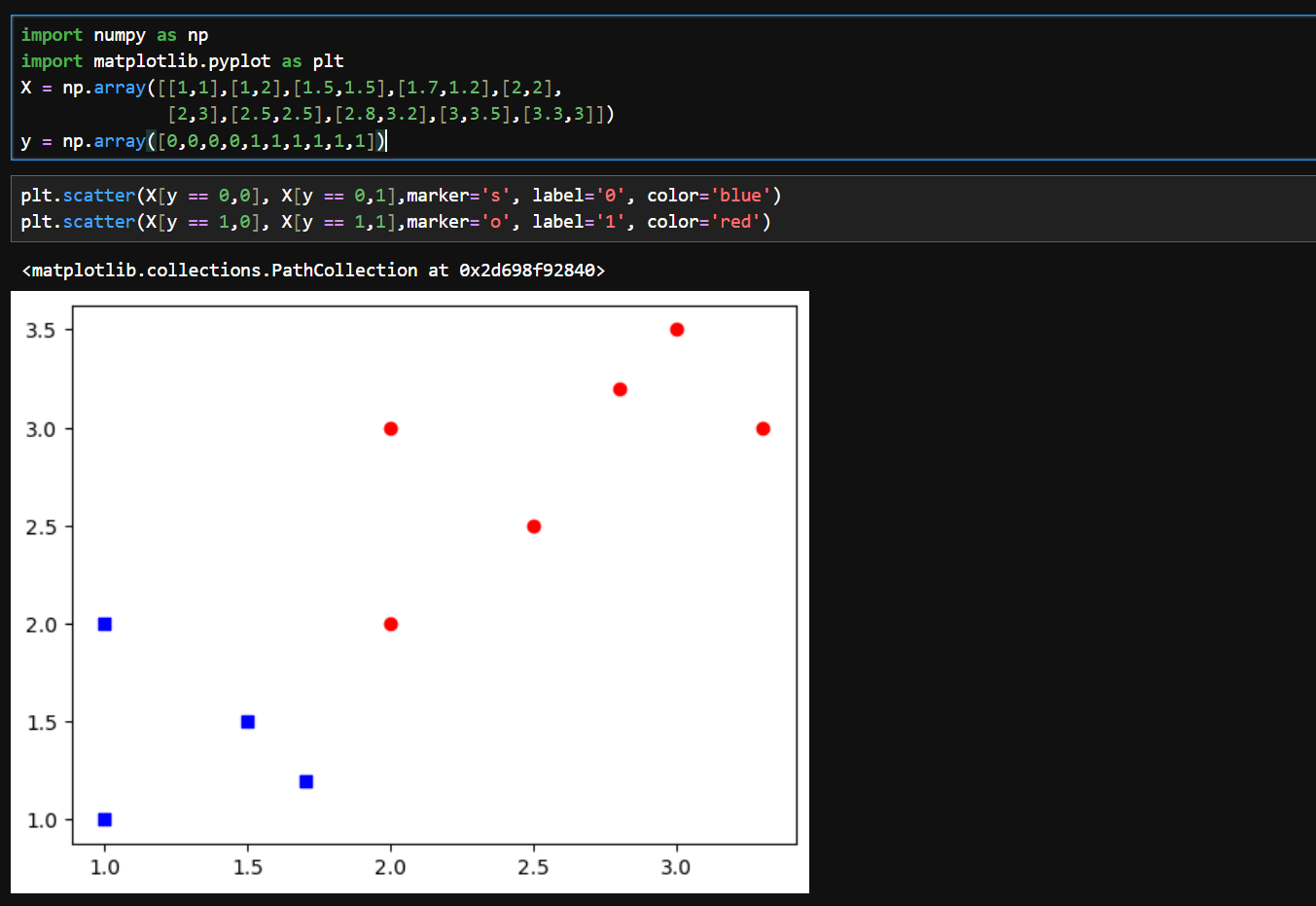
test_samples = np.array([[2.7,3],[1.8,1.8]])
# x轴：test_samples[:,0]: 取所有样本的第一列，也就是 (2.7)
# y轴：test_samples[:,1]:取所有样本的第二列，也就是 (3)
# 所以（x,y）=(2.7,3);另一个数据同理
plt.scatter(test_samples[:,0],test_samples[:,1],marker='x',color='green')

2、欧几里得距离（案例分析）

1. 数据准备

假设 X 是一个形状为 (m, n) 的二维 NumPy 数组，其中 m 是训练样本的数量，n 是每个样本的特征数量；test_sample 是一个形状为 (n,) 的一维 NumPy 数组，表示单个测试样本。

import numpy as np

# 训练样本集 X，包含 3 个样本，每个样本有 2 个特征
X = np.array([[1, 2], [3, 4], [5, 6]])
# 测试样本
test_sample = np.array([2, 3])

2. 广播操作（X - test_sample）

X - test_sample 这一步运用了 NumPy 的广播机制。广播机制允许 NumPy 在不同形状的数组之间进行算术运算。在这个例子中，test_sample 会被广播扩展成与 X 形状相同的数组，然后进行逐元素相减。

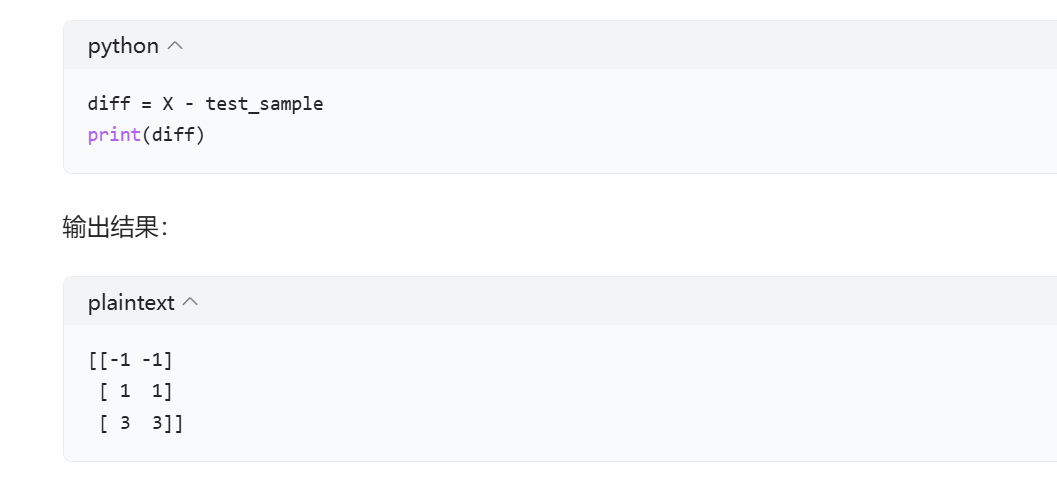
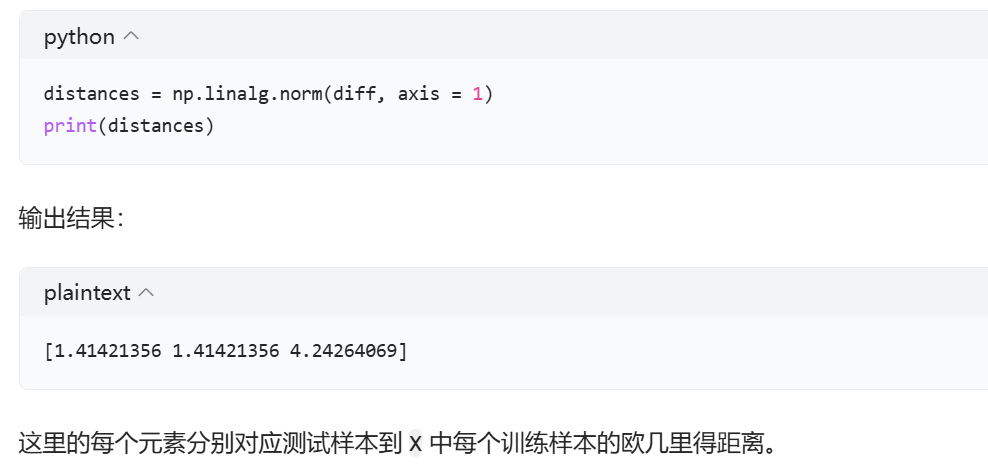
3. 计算欧几里得范数（np.linalg.norm(..., axis = 1)）

欧几里得范数也就是向量的长度，对于一个 n 维向量 v=[v1​,v2​,⋯,vn​]，其欧几里得范数的计算公式为：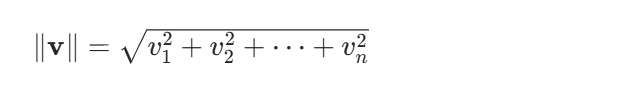

np.linalg.norm(diff, axis = 1) 会按行计算 diff 数组中每个向量的欧几里得范数，axis = 1 表示沿着行的方向进行计算。

3、综合

import numpy as np
import matplotlib.pyplot as plt
X = np.array([[1,1],[1,2],[1.5,1.5],[1.7,1.2],[2,2],
              [2,3],[2.5,2.5],[2.8,3.2],[3,3.5],[3.3,3]])
y = np.array([0,0,0,0,1,1,1,1,1,1])

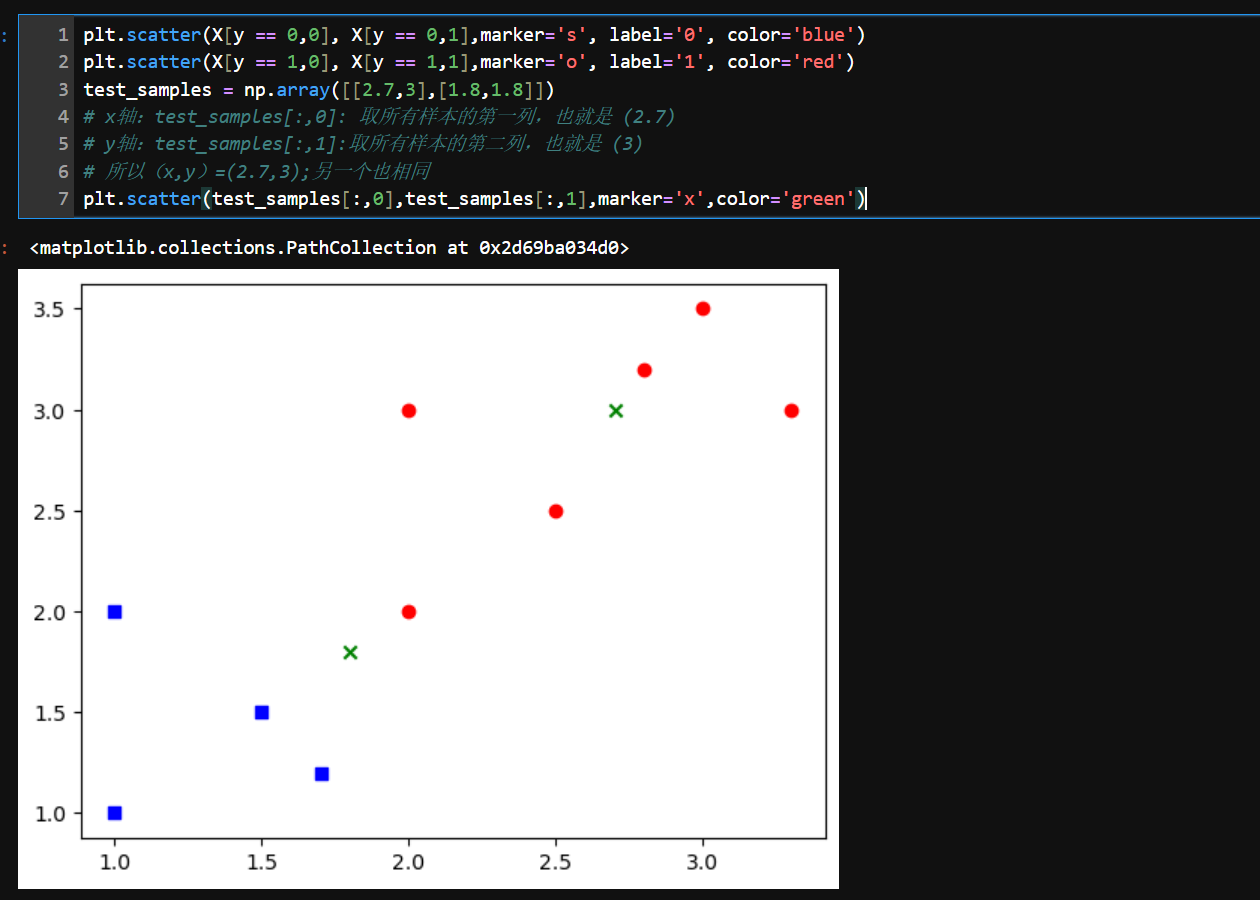
plt.scatter(X[y == 0,0], X[y == 0,1],marker='s', label='0', color='blue')
plt.scatter(X[y == 1,0], X[y == 1,1],marker='o', label='1', color='red')
test_samples = np.array([[2.7,3],[1.8,1.8]])
# x轴：test_samples[:,0]: 取所有样本的第一列，也就是 (2.7)
# y轴：test_samples[:,1]:取所有样本的第二列，也就是 (3)
# 所以（x,y）=(2.7,3);另一个也相同
plt.scatter(test_samples[:,0],test_samples[:,1],marker='x',color='green')

# 设置 k 值，k 表示要找出的距离测试样本最近的训练样本的数量
k = 3

# 遍历测试样本数组 test_samples，enumerate 函数会同时返回样本的索引 i 和样本本身 test_sample
for i, test_sample in enumerate(test_samples):
    # 计算当前测试样本到训练样本集 X 中每个样本的距离
    # X - test_sample 利用广播机制将 test_sample 与 X 中的每一行相减
    # np.linalg.norm 用于计算向量的欧几里得范数，axis = 1 表示按行计算，得到一个包含每个训练样本到测试样本距离的一维数组
    distances = np.linalg.norm(X - test_sample, axis = 1)
    
    # 对距离数组 distances 进行排序，并获取排序后元素的索引
    # np.argsort 函数返回的是排序后元素在原数组中的索引
    # [:k] 切片操作选取前 k 个索引，这些索引对应的训练样本就是距离当前测试样本最近的 k 个样本
    nearest_indices = np.argsort(distances)[:k]
    # print(nearest_indices)
    
    # 根据最近邻样本的索引，从训练样本集 X 中提取出这 k 个最近邻样本
    # 得到一个二维数组，每一行代表一个最近邻样本:[[2.8 3.2]
    #                                         [2.5 2.5]
    #                                         [3.  3.5]]
    #                                        [[2.  2. ]
    #                                        [1.5 1.5]
    #                                         [1.7 1.2]]
    nearest_samples = X[nearest_indices]

    # 根据当前测试样本的索引 i 来选择绘制散点时使用的标记形状
    # 如果是第一个测试样本（i == 0），使用菱形标记 'D'
    # 否则，使用五角星标记 'P'
    if i == 0:
        marker = 'D'
    else:
        marker = 'P'
    
    # 使用 matplotlib 的 scatter 函数绘制最近邻样本的散点图
    # nearest_samples[:, 0] 表示选取最近邻样本的第一列作为 x 坐标
    # nearest_samples[:, 1] 表示选取最近邻样本的第二列作为 y 坐标
    # facecolors='none' 表示散点是空心的，没有填充颜色
    # edgecolors='green' 表示散点的边缘颜色为绿色
    # s=200 表示散点的大小为 200
    # marker=marker 表示使用之前选择的标记形状
    plt.scatter(nearest_samples[:, 0], nearest_samples[:, 1], facecolors='none', edgecolors='green', s=200, marker=marker)
    
    # 遍历最近邻样本的索引
    # enumerate 函数会同时返回索引的序号 j 和实际索引 index
    for j, index in enumerate(nearest_indices):
        # 使用 matplotlib 的 annotate 函数为每个最近邻样本添加注释
        # f'N{j + 1}' 是注释的文本内容，例如 'N1'、'N2' 等，表示第几个最近邻样本
        # (X[index, 0], X[index, 1]) 是注释的位置，即最近邻样本在图中的坐标
        # textcoords="offset points" 表示注释文本的坐标系统是相对于注释位置的偏移量
        # xytext=(0, 10) 表示注释文本相对于注释位置在 x 方向上偏移 0 个点，在 y 方向上偏移 10 个点
        # ha='center' 表示注释文本的水平对齐方式为居中
        plt.annotate(f'N{j + 1}', (X[index, 0], X[index, 1]), textcoords="offset points", xytext=(0, 10), ha='center')

plt.xlabel('X1')
plt.ylabel('X2')
plt.legend([0,1])
plt.show()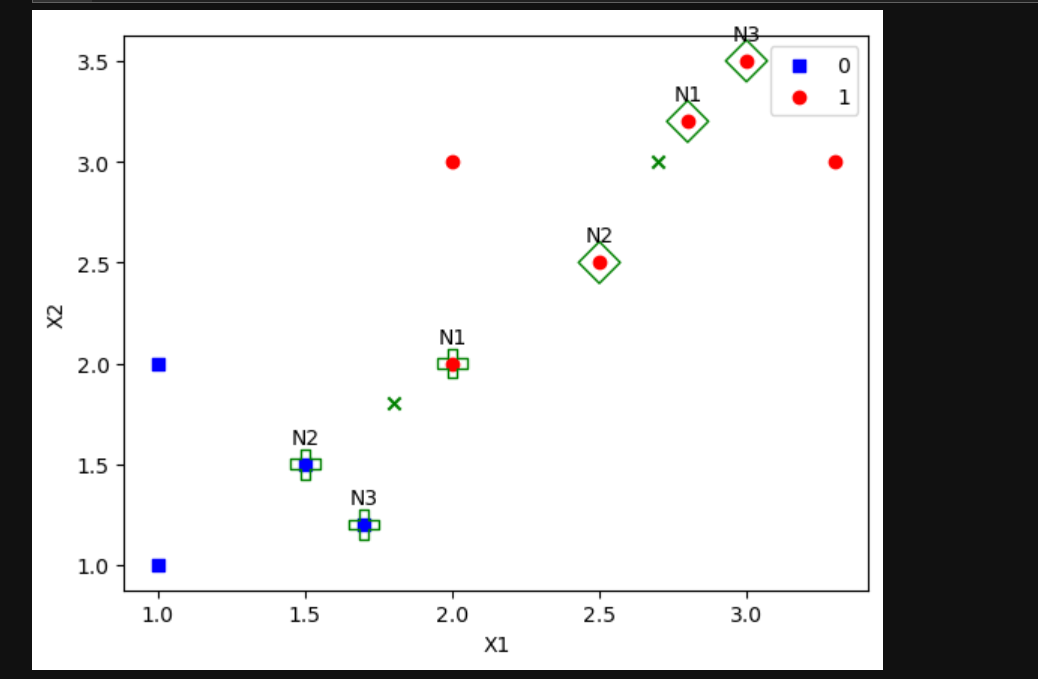

四、使用k近邻分类器预测燕尾花类型

1、数据集分析

1.1导入需要的库

# 导入 pandas 库并将其别名为 pd，pandas 是一个强大的数据处理和分析库，常用于数据读取、清洗、转换等操作
import pandas as pd
# 导入 seaborn 库并将其别名为 sns，seaborn 是基于 matplotlib 的数据可视化库，提供了更高级、美观的统计图形绘制功能
import seaborn as sns
# 从 sklearn.datasets 模块中导入 load_iris 函数，该函数用于加载经典的鸢尾花数据集，常用于机器学习和数据分析的示例和测试
from sklearn.datasets import load_iris

1.2 查看数据集的信息

# 加载鸢尾花数据集到Bunch对象
# 作用：从sklearn获取标准分类数据集，用于分类任务基准测试
# 对象属性：data(特征数据), target(类别标签), feature_names(特征说明)等
iris = load_iris()

# 打印数据集描述文档
# 内容包含：样本数量、特征统计摘要、作者信息等元数据
# 数据分析价值：帮助快速掌握数据分布和字段含义，指导后续预处理
print("数据集基本信息：")
print(iris.DESCR)  # DESCR = DESCRiption 的缩写，包含完整数据集文档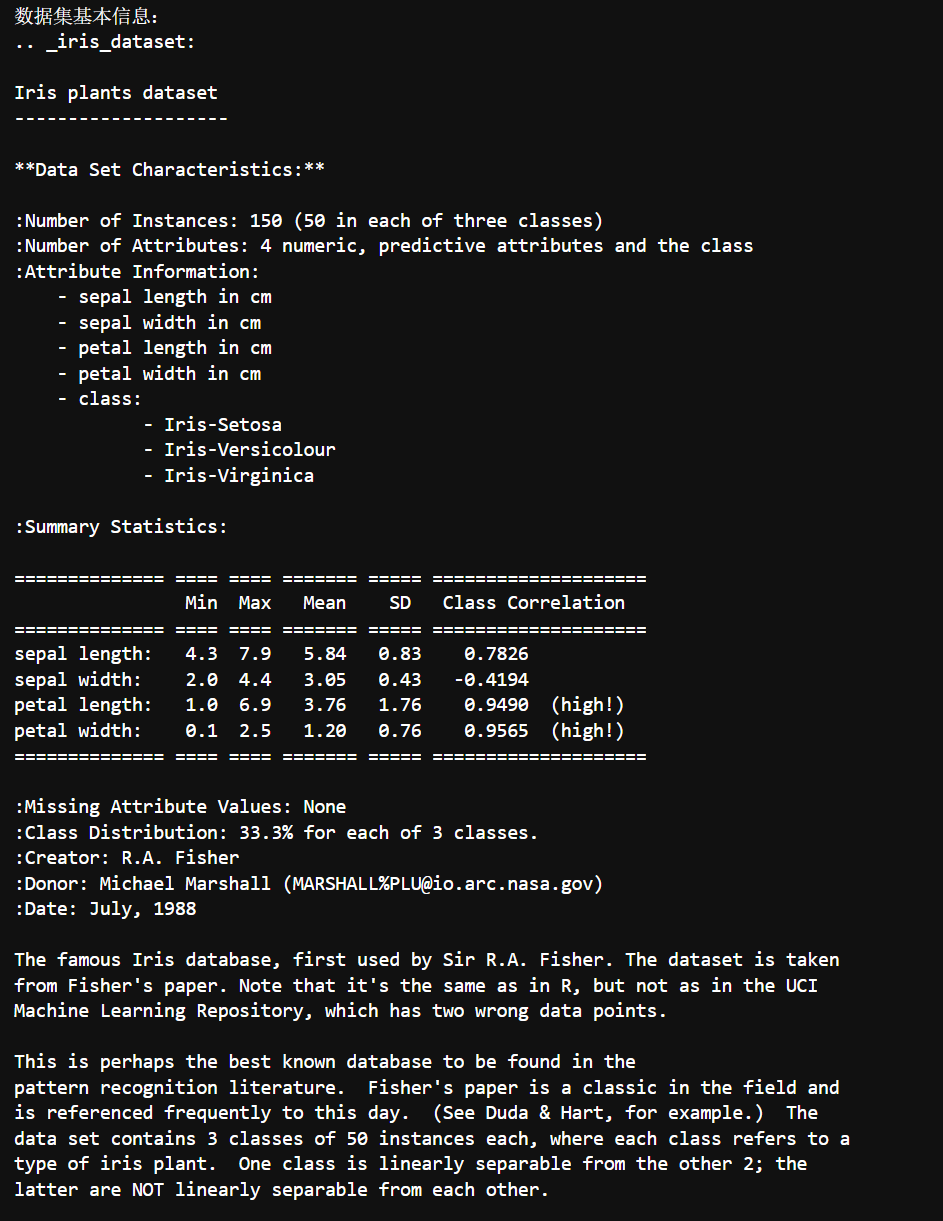

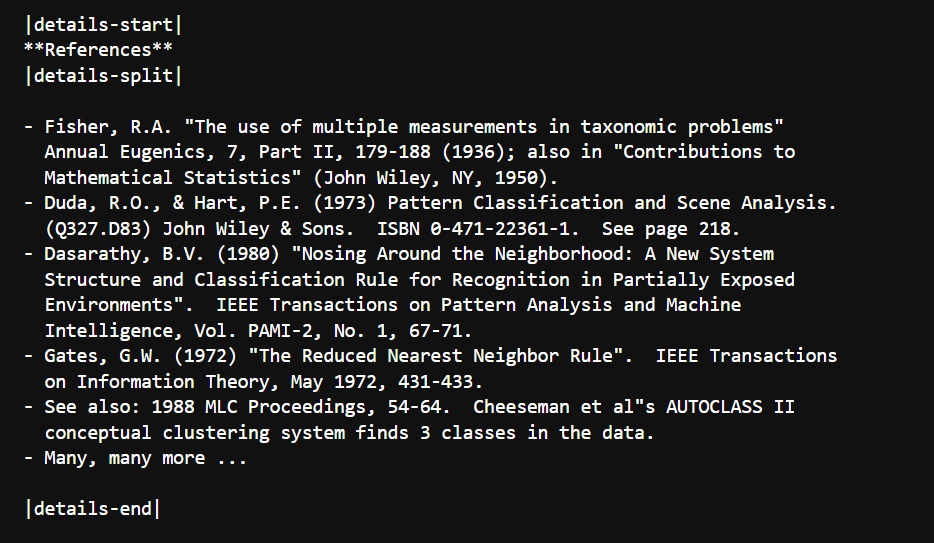
以下是对Iris数据集的系统分析，分为关键特征、统计洞察和应用方向三个维度：

---

1.2.1关键特征解析

1. 数据结构

   • 150个样本均衡分布在3个类别（各50个）

   • 4个数值特征：花萼长/宽、花瓣长/宽（单位：cm）

   • 无缺失值，数据完整度高

2. 特征特性

   • 花瓣特征（长度3.76±1.76cm，宽度1.20±0.76cm）比花萼特征（长度5.84±0.83cm，宽度3.05±0.43cm）方差更大

   • 花瓣尺寸与类别强相关（相关系数>0.95），是重要分类指标

---

1.2.2统计洞察

1. 类别分离特性

   • Setosa线性可分（花瓣尺寸显著小于其他两类）

   • Versicolour与Virginica非线性可分（需复杂决策边界）

2. 特征相关性矩阵

   	Sepal Len	Sepal Wid	Petal Len	Petal Wid
   Class	0.7826	-0.4194	0.9490	0.9565

3. 异常值提示

   • 花瓣宽度存在极端值（0.1cm最小值到2.5cm最大值）

   • 花萼长度最大达7.9cm（高于均值+2σ=7.5cm）

1.3查看特征

# 利用 pandas 的 DataFrame 类创建一个数据框 df
# data 参数指定为 iris.data，即鸢尾花数据集的特征数据
# columns 参数指定为 iris.feature_names，即鸢尾花数据集的特征名称，作为数据框的列名
df = pd.DataFrame(data = iris.data, columns=iris.feature_names)
# 向数据框 df 中添加一个名为 'target' 的新列
# 该列的值为 iris.target，即鸢尾花数据集的类别标签
df['target'] = iris.target
# 打印提示信息，表明接下来要输出数据的前5行
print("数据的前5行：")
# 调用数据框的 head 方法，默认返回数据框的前5行数据
# 并将结果打印输出，方便查看数据的基本结构和内容
print(df.head())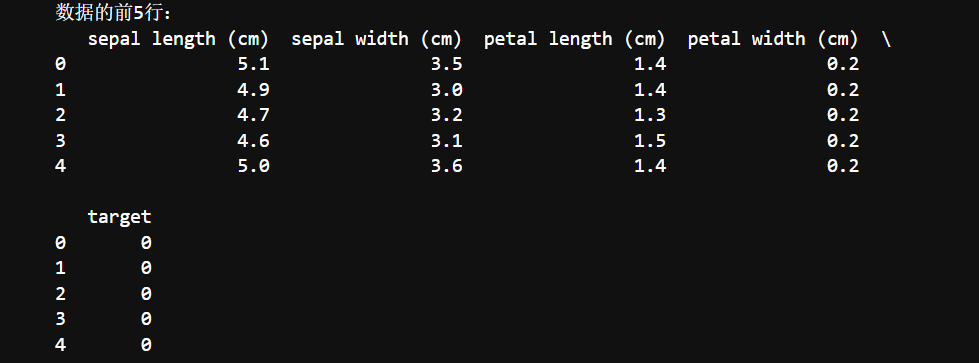

1.4统计

print("数据框统计信息：")
# 调用数据框的 describe 方法，该方法会计算并返回数据框中数值列的统计信息
# 统计信息包括计数、均值、标准差、最小值、25%分位数、中位数、75%分位数和最大值
print(df.describe())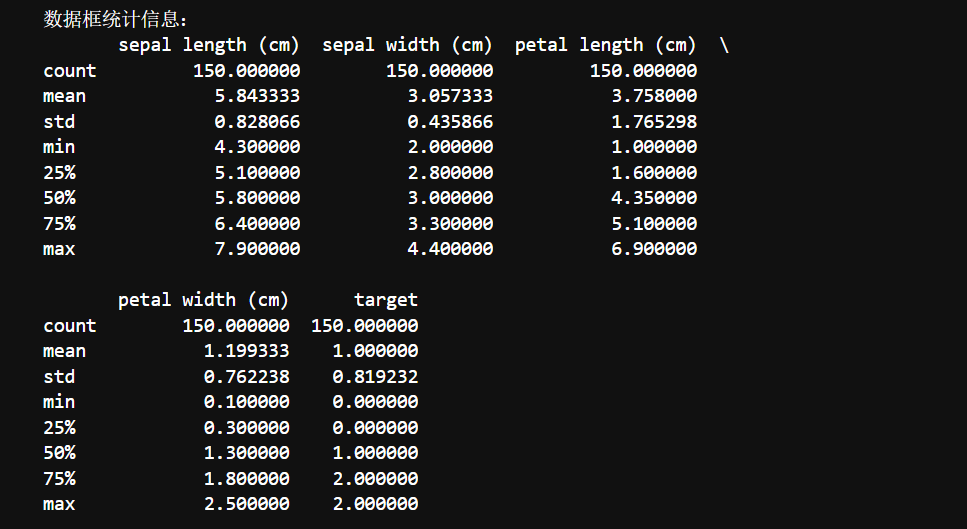

1.5画出特征的柱形图

# 使用 seaborn 库的 countplot 函数绘制柱状图
# x='target' 表示以数据框 df 中的 'target' 列作为分类依据，统计每个类别出现的频次
# data=df 明确指定使用的数据来源为数据框 df
# 该柱状图可以直观地展示不同类别（'target' 列的值）的样本数量分布情况
sns.countplot(x='target', data=df)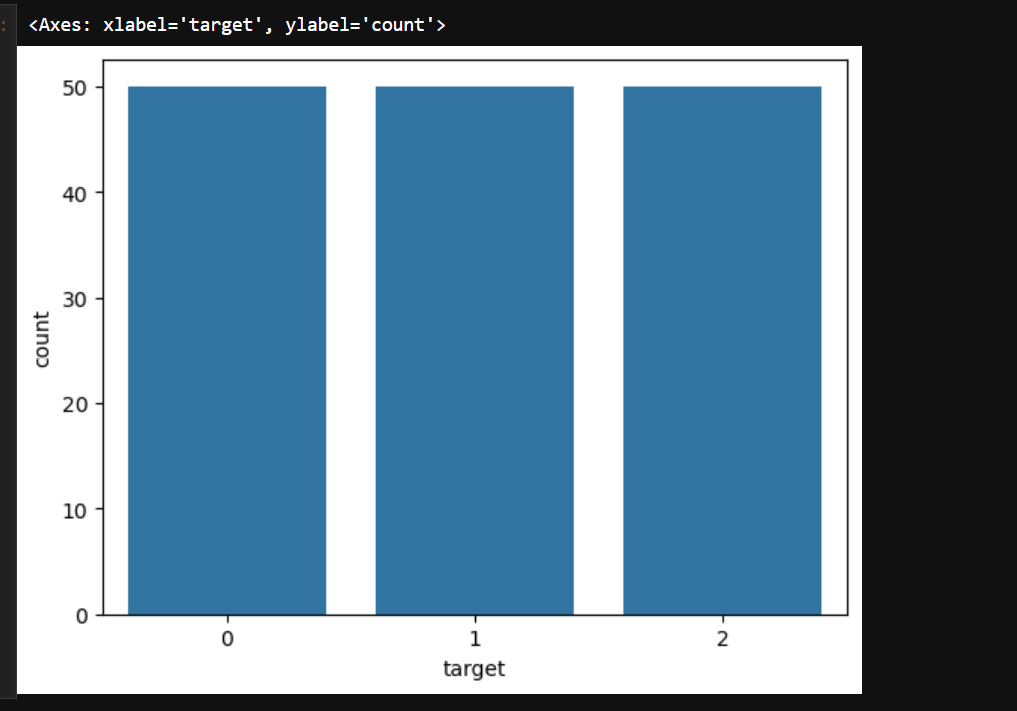

1.6画出散点图

# 使用 seaborn 库的 pairplot 函数创建一个散点图矩阵
# df 是要绘制的数据框，包含了鸢尾花数据集的特征和目标标签
# hue='target' 指定根据 'target' 列的值对数据进行分类着色
# 这意味着散点图矩阵中的每个子图会根据不同的 'target' 类别（即鸢尾花的不同种类）使用不同的颜色来区分
# 这样可以直观地观察不同类别在各个特征组合下的分布情况，有助于发现特征之间的关系以及不同类别之间的差异
sns.pairplot(df, hue='target')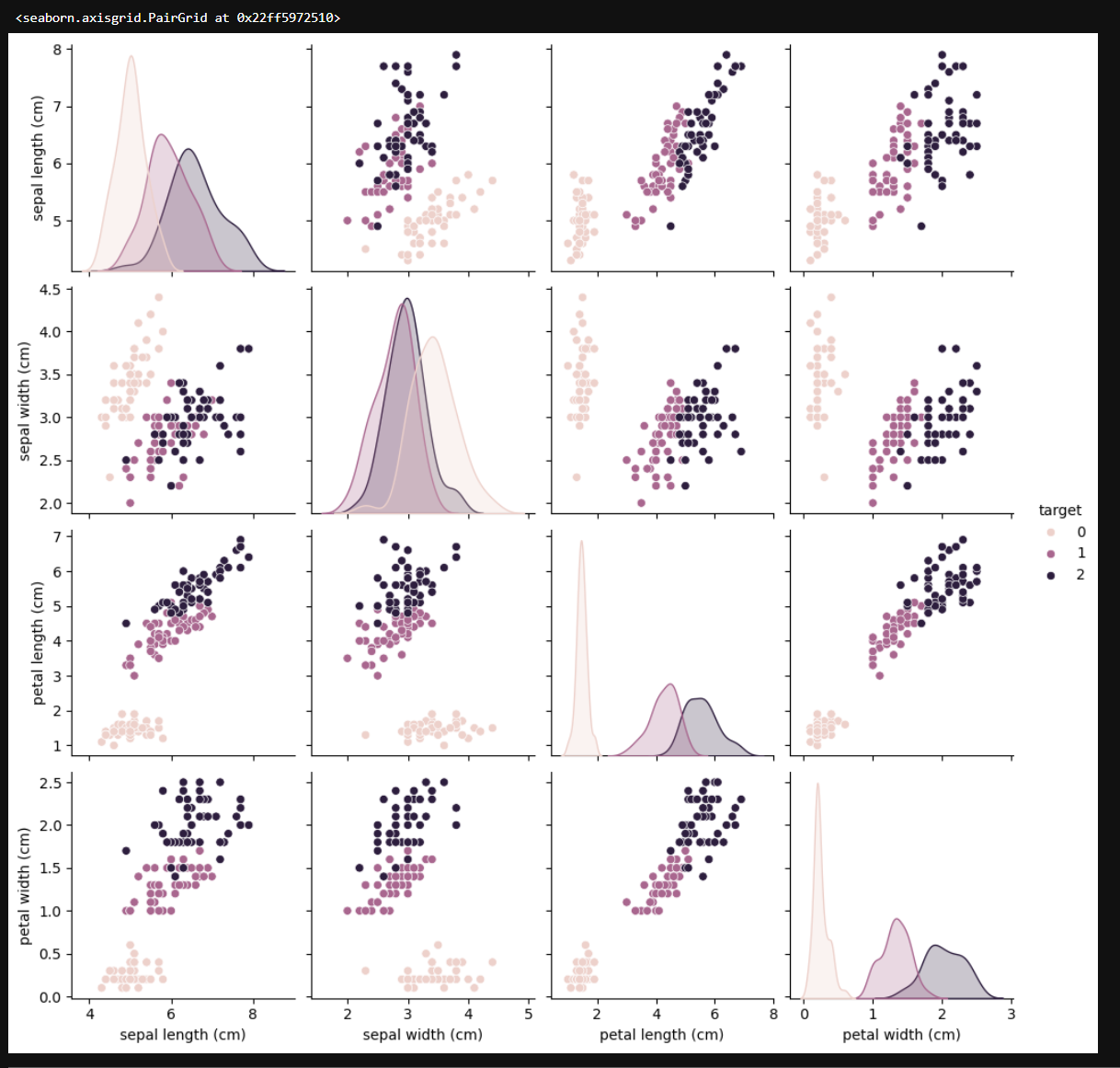

特征	统计量	类别 0	类别 1	类别 2
萼片长度（cm）	均值	5.006	5.936	6.588
	中位数	5.0	6.0	6.6
	标准差	0.352	0.516	0.636
萼片宽度（cm）	均值	3.418	2.770	2.974
	中位数	3.4	2.8	3.0
	标准差	0.381	0.314	0.322
花瓣长度（cm）	均值	1.462	4.260	5.552
	中位数	1.5	4.35	5.5
	标准差	0.174	0.470	0.551
花瓣宽度（cm）	均值	0.246	1.326	2.026
	中位数	0.2	1.3	2.0
	标准差	0.105	0.197	0.274

1.7保存文件

# 创建一个名为 iris_df 的 DataFrame 对象
# 利用 pandas 的 DataFrame 构造函数，将 iris 数据集中的特征数据（iris.data）作为数据内容
# 并将 iris 数据集中的特征名称（iris.feature_names）作为列名
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
# 为 iris_df 这个 DataFrame 添加一个新的列，列名为 'target'
# 该列的值来自于 iris 数据集中的目标标签（iris.target）
iris_df['target'] = iris.target
# 将 iris_df 这个 DataFrame 保存为 CSV 文件
# 文件名为 'iris_dataset.csv'，index=False 表示在保存文件时不将 DataFrame 的索引保存到文件中
iris_df.to_csv('iris_dataset.csv', index=False)