【opencv】第9章 图像梯度 -- 9.3 Laplacian 算子
上面的式子,用在图像里,可以看作是 上、下、左、右点的求和,减去中心点的4倍。所以,对图像做拉普拉斯变换,可以看作是 用原图像 与下面的模板做卷积运算,下面的这个模版(mask 或叫做 filter)也就是拉普拉斯算子了。因为在求一阶偏导函数的时候,我们是通过 x+1 的形式来近似求 x点 的偏导的,直观上来讲,有点偏右了,所以在求二阶导函数的时候,我们让。以上的拉普拉斯变换公式,应用在连续的函数
1、拉普拉斯变换
拉普拉斯变换的定义为: L a p l a c i a n = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 Laplacian = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} Laplacian=∂x2∂2f+∂y2∂2f
就是对原图像的 x方向 和 y方向,分别做 2阶偏导数,然后相加。
以上的拉普拉斯变换公式,应用在连续的函数中,我们应该都会求解的,但是在图像这个离散的二维环境中,怎么做拉普拉斯变化呢,具体怎么计算呢?我们往下看:
我们知道连续的一阶导函数公式如下:
f ′ ( x 0 ) = l i m Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0) = lim_{\Delta x \rightarrow 0} \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x} f′(x0)=limΔx→0Δxf(x0+Δx)−f(x0)
那么,离散的一阶导函数公式为:
f ′ ( x 0 ) = l i m Δ x → 1 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = f ( x 0 + 1 ) − f ( x 0 ) f'(x_0) = lim_{\Delta x \rightarrow 1}\frac{f(x_0+\Delta x) - f(x_0)}{\Delta x} = f(x_0+1)-f(x_0) f′(x0)=limΔx→1Δxf(x0+Δx)−f(x0)=f(x0+1)−f(x0)
所以,图像在 x , y x, y x,y 两个方向上的一阶偏导数分别为:
∂ f ∂ x = f ( x + 1 , y ) − f ( x , y ) ∂ f ∂ y = f ( x , y + 1 ) − f ( x , y ) \frac{\partial f}{\partial x} = f(x+1 ,y) - f(x, y) \\ \ \\ \frac{\partial f}{\partial y} = f(x, y+1) - f(x, y) ∂x∂f=f(x+1,y)−f(x,y) ∂y∂f=f(x,y+1)−f(x,y)
然后,在一阶偏导函数的基础上,求二阶偏导函数。因为在求一阶偏导函数的时候,我们是通过 x+1 的形式来近似求 x点 的偏导的,直观上来讲,有点偏右了,所以在求二阶导函数的时候,我们让 x = x − 1 x=x-1 x=x−1 来近似 x x x 点,更为恰当,所以,在 x , y x, y x,y 方向上的二阶偏导数分别为:
∂ 2 f ∂ x 2 = ∂ [ f ( x + 1 , y ) − f ( x , y ) ] ∂ x = ∂ f ( x + 1 , y ) ∂ x − f ( x , y ) ∂ x = [ f ( x + 1 , y ) − f ( x ) ] − [ f ( x , y ) − f ( x − 1 , y ) ] = f ( x − 1 , y ) + f ( x + 1 , y ) − 2 f ( x , y ) ∂ 2 f ∂ y 2 = ∂ [ f ( x , y + 1 ) − f ( x , y ) ] ∂ y = ∂ f ( x , y + 1 ) ∂ y − f ( x , y ) ∂ y = [ f ( x , y + 1 ) − f ( x , y ) ] − [ f ( x , y ) − f ( x , y − 1 ) ] = f ( x , y − 1 ) + f ( x , y + 1 ) − 2 f ( x , y ) \begin{aligned} \frac{\partial^2 f}{\partial x^2} &= \frac{\partial [f(x+1, y) - f(x, y)] }{\partial x} \\ \ \\ &= \frac{\partial f(x+1, y)}{\partial x} - \frac{f(x, y)}{\partial x} \\ \ \\ &= [f(x+1,y) - f(x)] - [f(x, y) - f(x-1, y)] \\ \ \\ &=f(x-1, y) + f(x+1, y) - 2 f(x, y)\\ \ \\ \frac{\partial^2 f}{\partial y^2} &= \frac{\partial [f(x, y+1) - f(x, y)] }{\partial y} \\ \ \\ &= \frac{\partial f(x, y+1)}{\partial y} - \frac{f(x, y)}{\partial y} \\ \ \\ &= [f(x, y+1) - f(x,y)] - [f(x,y) - f(x,y-1)] \\\ \\ &=f(x,y-1) + f(x,y+1) - 2 f(x,y) \end{aligned} ∂x2∂2f ∂y2∂2f =∂x∂[f(x+1,y)−f(x,y)]=∂x∂f(x+1,y)−∂xf(x,y)=[f(x+1,y)−f(x)]−[f(x,y)−f(x−1,y)]=f(x−1,y)+f(x+1,y)−2f(x,y)=∂y∂[f(x,y+1)−f(x,y)]=∂y∂f(x,y+1)−∂yf(x,y)=[f(x,y+1)−f(x,y)]−[f(x,y)−f(x,y−1)]=f(x,y−1)+f(x,y+1)−2f(x,y)
再由拉普拉斯算子的定义,把上面的两个式子求和,就得到了:
L a p l a c i a n = f ( x − 1 , y ) + f ( x + 1 , y ) + f ( x , y − 1 ) + f ( x , y + 1 ) − 4 f ( x , y ) Laplacian = f(x-1, y) + f(x+1, y) + f(x,y-1) + f(x,y+1) - 4 f(x, y) Laplacian=f(x−1,y)+f(x+1,y)+f(x,y−1)+f(x,y+1)−4f(x,y)
上面的式子,用在图像里,可以看作是 上、下、左、右点的求和,减去中心点的4倍。所以,对图像做拉普拉斯变换,可以看作是 用原图像 与下面的模板做卷积运算,下面的这个模版(mask / filter)也就是拉普拉斯算子了。

2、拉普拉斯算子(Laplacian 算子)
Laplacian 算子 (拉普拉斯算子)是一种二阶导数算子,其具有旋转不变性,可以满足不同方向的边缘锐化。

计算像素点P5的近似二阶导数值入下: P 5 l a p = ( P 2 + P 4 + P 6 + P 8 ) − 4 ⋅ P 5 P5_{lap} = (P2 + P4 + P6 + P8) - 4 \cdot P5 P5lap=(P2+P4+P6+P8)−4⋅P5
上面介绍的默认的拉普拉斯算子 只考虑了上下左右的情况,并没有考虑斜对角线方向的情况,如果连斜对角线的情况也考虑进来的话,我们就有了 拓展版的拉普拉斯算子:

默认的拉普拉斯算子只在 90度方向上存在旋转不变性,而拓展模版则在45度方向上也具有旋转不变性。
opencv 中 函数原型:
dst_img = cv2.Laplacian(src_img, ddepth, dx, dy, ksize, scale, delta)
参数:
- dst_img:结果图像
- src_img:原始图像
- ddepth:输出图像的深度。 默认是1,采用的是3x3的核。
- dx:x方向上的求导阶数,值为0时,表示在该方向上没有求导
- dy:y方向上的求导阶数,值为0时,表示在该方向上没有求导
- ksize:Sobel核的大小。该值为-1时,会使用Scharr算子进行计算。
- scale:代表计算导数值时的缩放因子。默认值是1,表示没有缩放。
- delta:代表加到目标图像上的亮度值。默认值是0。
举例:
import cv2
src_img = cv2.imread("sobel.bmp", 0)
laplacian = cv2.Laplacian(src_img, cv2.CV_64F)
laplacian = cv2.convertScaleAbs(laplacian)
cv2.imshow('src_img', src_img)
cv2.imshow('sobel_y', laplacian)
cv2.waitKey()
cv2.destroyAllWindows()
输出为: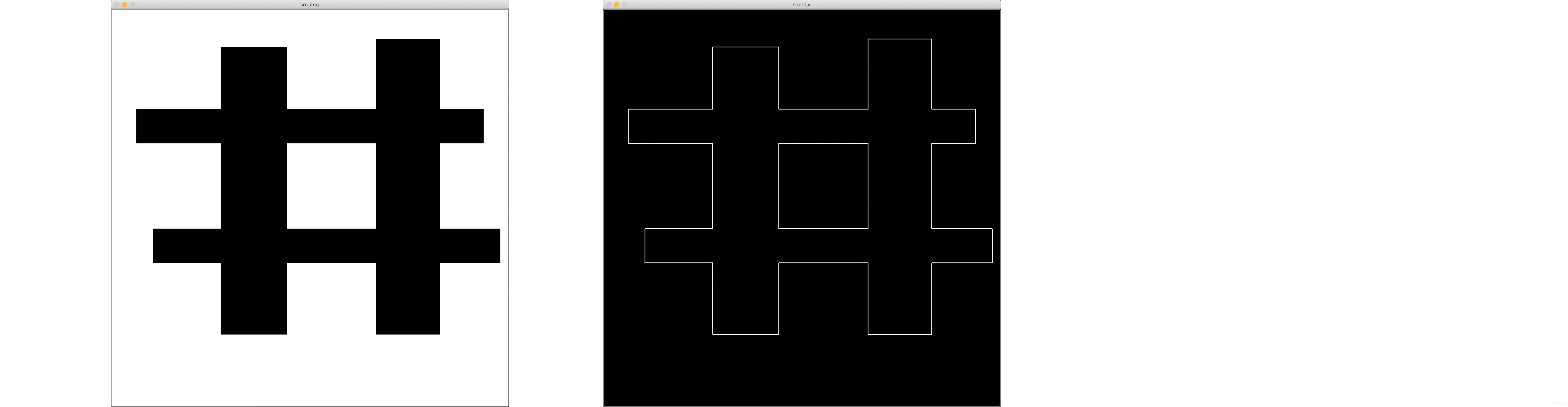
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容








所有评论(0)