一、概述：

1. RNN Encoder–Decoder for Statistical Machine Translation论文连接：http://emnlp2014.org/papers/pdf/EMNLP2014179.pdf

2. 摘要：

在本文中，作者提出了一种称为RNN编码器-解码器的新型神经网络模型-由两个循环解码器组成神经网络。一个RNN作为编码器将一系列符号编码为固定长度的向量表示，另一个RNN作为解码器将固定长度的向量表示形式解码为另一个符号序列。所提出模型的编码器和解码器是联合训练的，最大化在给定源序列的情况下得出目标序列的条件概率。通过使用RNN编码器- 解码器计算的短语对的条件概率作为现有对数线性中的附加功能模型。

二、具体实现

1. RNN Encoder–Decoder

1.1 Preliminary: Recurrent Neural Networks

RNN循环神经网络是整个模型的基础组件，原理在这里我们不再详述

1.2 RNN Encoder–Decoder

在这篇论文，作者提出一种新型的神经网络架构，即：encoder将可变长序列编码成定长向量表达，然后解码器将这个定长的向量解码成变长序列。从概率视角看，新模型是一种通用方法，去学习一个以可变长度序列为条件得到另一个可变长度序列的条件概率：$P(y_1,y_2,...,y_{T^{\prime }}|x_1,x_2,...,x_T)$，这里注意：输入序列长度T和输出序列长度T’可能是不同的。

1. 其中的encoder是RNN，作用是顺序的读取输入序列x中的每个符号；根据RNN原理当读取每个符号的时候RNN的hidden state都会不同；当读取到序列的最后一个符号的时候，认为RNN的hidden state这时已经包含了整个输入序列的特征。
2. 模型中的decoder是另外一个RNN，它的主要作用是生成输出序列中的y； 它不像传统的RNN只接收 hidden state 和 $y_{(t-1)}$，还增加了encoder的hidden state输出c。因此，decoder在时间步t的 hidden state为：
   $$h_{(t)}=f(h_{(t-1)},y_{t-1},c)$$
   相应的，t时间步y的输出为：
   $$P(y_t|y_{t-1},y_{t-2},...,y_1,c)=g(h_t,y_{t-1},c)$$
   其中f和g是激活函数。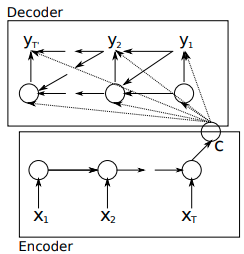
   
3. 编码器-解码器经过联合训练，以最大限度地提高条件概率
   $$ma{x}_{\theta }\frac{1}{N}\sum _{n=1}^{N}logp\theta (y_n|x_n)$$
   其中$\theta$是模型的参数集，$x_n$和$y_n$是输入序列和输出序列。
   由于解码器的输出，从输入开始，是可微分的，我们可以使用基于梯度的算法来估计模型参数。
4. 模型可以有两种使用方式：
   1）使用模型根据源序列生成目标序列
   2）给定输入序列和输出序列，根据$P_{\theta }(y|x)$ 计算概率，可以转换为评分

1.3 自适应记忆或遗忘的隐藏单元（GRU）

1. 另外作者提出了一种新型的隐藏单元，它收到LSTM计算单元的启发，但是计算和实现更加简单。请看下图：
   
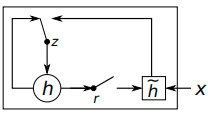
   其中gate z选择hidden state h是否被新的hidden state $\hat{h}$更新， reset gate r判断是否忽略上一次的hidden state。
2. 第j个时间步隐藏单元的计算逻辑如下
   reset gate:
   $r_j=\sigma ([W_{r}x{]}_j+[U_r{h}_{(}t-1){]}_j)$
   $\sigma$是sigmoid函数，
   $[{]}_j$中的x表示第j个时间步输入向量， $h_{t-1}$表示前一个时间步的hidden state.
   $W_r$和$U_r$表示学习到的权重矩阵
   update gate:
   $z_j=\sigma ([W_{z}x{]}_j+[U_z{h}_{(t-1)}{]}_j)$
   hidden state:
   $h_j^{(t)}=z_j{h}_j^{(t-1)}+(1-z_j){\hat{h}}_j^{(t)}$
   其中${\hat{h}}_j^{(t)}$计算逻辑为：
   ${\hat{h}}_j^{(t)}=\varphi ([Wx{]}_j+[U(r\odot h_{(t-1)}){]}_j)$

在这个公式中，如果r为0， 则当前的hidden state会强制忽略之前的 hidden state 而只关注当前的输入 x。一方面，hidden state可以删除任何明确的无效信息， 另一方面， update gate可以控制，多少信息来源于上一个时间步的hidden state. 这里和 LSTM的memory cell 比较相似，帮助RNN记住long-term信息。
由于每个隐藏单元都有单独的重置和更新门，每个隐藏单元将学习捕获不同时间尺度上的依赖关系。

2 Statistical Machine Translation

在常用的统计机器翻译系统中，目标是通过给定的源序列e找到翻译f，使得条件概率最大化：
$p(f|e)\propto p(e|f)p(f)$
其中右侧的第一项称为翻译模型和后面的语言模型，大部分SMT系统模型$logp(f|e)$是对数线性模型：
$logp(f|e)={\sum }_{n=1}^N{w}_n{f}_n(f,e)+logZ(e)$
其中 $f_n$和$w_n$分别是第n时间步的特征和权重。Z(e)是归一化常数不依赖于权重。权重为通常经过优化，以最大限度地提高BLEU分数。

2.1 Scoring Phrase Pairs with RNN Encoder–Decoder

在这里，我们建议在短语对表上训练RNN编码器 -解码器 （见第2.2节）并在调整 SMT 解码器时，将其分数用作等式中对数线性模型中的附加特征。
当我们训练RNN编码器解码器时，我们要忽略每个短语对在原始语料库的出现频率。这种方法主要是为了减少根据归一化频率从大型短语表中随机选择短语对的计算复杂度。确保 RNN 编码器 –解码器不是只简单地根据它们的出现次数对短语对进行排名。
这样做的一个根本原因是：短语表中的现有翻译概率已经反映了原始语料库中短语对的频率。

3. 验证效果：BLUE分数

未完待续。。。