随机向量函数的分布

• 背景：当随机变量$X_1,X_2,...,X_n$的联合分布已知时，如何求出它们的函数$Y_i=g_i(X_1,X_2,...,X_n),i=1,2,...,m$的联合分布

• 离散型分布的情形：

  若X、Y独立，$P(X=k)=a_k,k=0,1,2,...,P(Y=k)=b+k,k=0,1,...$,求$Z=X+Y$的概率函数

  $$\begin{gathered} P(Z=r)=P(X+Y=r)={\sum }_{i=0}^{r}P(X=i,Y=r-i)={\sum }_{i=0}^{r}P(X=i)P(Y=r-i) \\ =a_0{b}_r+a_1{b}_{r-1}+...+a_r{b}_0 \end{gathered}$$

  此即离散卷积公式

• 连续型分布的情形

  设X和Y的联合密度为$f(x,y)$，求$Z=X+Y$的密度

  解：$Z=X+Y$的分布函数是：
  $$F_Z(z)=P(Z\le z)=P(X+Y\le z)={\iint }_{D}f(x,y)dxdy$$
  
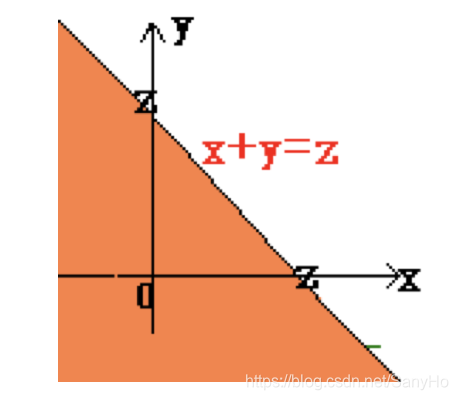
  这里积分区域D={(x,y):x+y≤z}D=\{(x,y):x+y\leq z\}D={(x,y):x+y≤z}，是直线$x+y=z$左下方的半平面。

  $\therefore$
  $$F_Z(z)={\iint }_{x+y\le z}f(x,y)dxdy$$
  化为累次积分，得

$$F_Z(z)={\int }_{-\infty }^{\infty }[{\int }_{-\infty }^{z-y}f(x,y)dx]dy$$

​ 固定z和y，对方括号内的积分作变量代换，令$x=u-y$，再交换积分次序，得
$$F_Z(z)={\int }_{-\infty }^{\infty }[{\int }_{-\infty }^{z}f(u-y,y)du]dy={\int }_{-\infty }^z[{\int }_{-\infty }^{\infty }f(u-y,y)dy]du$$
​ 由概率密度与分布密度的关系，即得$Z=X+Y$的概率密度为：
$$f_Z(z)=F_Z^{\prime }(z)={\int }_{-\infty }^{\infty }f(z-y,y)dy$$
​ 由X和Y的对称性，$f_Z(z)$又可写成
$$f_Z(z)=F_Z^{\prime }(z)={\int }_{-\infty }^{\infty }f(x,z-x)dx$$
​ 以上两式即是两个随机变量和的概率密度一般公式

​ 特别，当X和Y独立，设（X，Y）关于X，Y的边缘密度分别为$f_X(x),f_Y(y)$，则上述两式化为：
$$f_Z(z)={\int }_{-\infty }^{\infty }{f}_X(z-y)f_Y(y)dy$$

$$f_Z(z)={\int }_{-\infty }^{\infty }{f}_X(x)f_Y(z-x)dx$$

​ 这两个公式被称为卷积公式。

• 若X和Y独立，具有相同的分布$N(0,1)$，则$Z=X+Y$服从正态分布$N(0,2)$

  及若X和Y独立，$X$_{$N(\mu_1,\sigma_1^2)$,$Y$}$N(\mu ,{\sigma }_2^2)$,则$Z=X+Y$~$N({\mu }_1+{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)$

  此结论可以推广到n个独立随机变量之和。

  即有限个正态变量的线性组合任然服从正态分布。