一、为什么特征缩放

在面对多维特征问题的时，有时特征数据数据值相差过大，如在运用多变量线性回归预测房价模型中，房屋面积和卧室个数这俩个特征之间数值相差大，而要保证这些特征都具有相近的尺度，就要进行特征缩放，这能帮助梯度下降算法更快地收敛。如图：

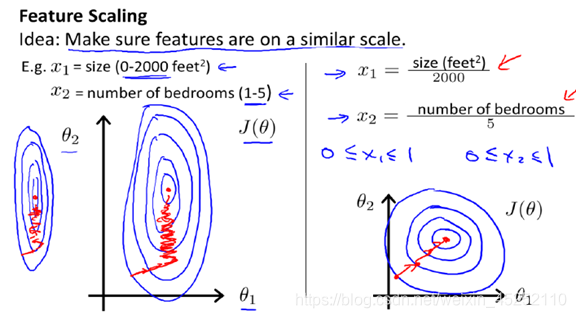
直接求解的缺点：
1、当x1 特征对应权重会比x2 对应的权重小很多，降低模型可解释性
2、梯度下降时，最终解被某个特征所主导，会影响模型精度与收敛速度
3、正则化时会不平等看待特征的重要程度（尚未标准化就进行L1/L2正则化是错误的）

特征缩放的好处：
1、提升模型收敛速度
2、提高模型精度

二、特征缩放常用的方法

特征缩放思想: 确保这些特征都处在一个相近的范围。
下面介绍俩种常用的特征缩放方法。

1、归一化特征缩放(0-1缩放)

python代码实现：

#数据预处理
def preprocess(X,y):
    #进行0-1缩放特征
    X_min = np.min(X)
    X_max = np.max(X)
    X = (X-X_min)/(X_max-X_min)

    #数据初始化
    X = np.c_[np.ones(len(X)),X]
    y = np.c_[y]
    return X,y
    
X,y = preprocess(X,y)

对应sklearn中的preprocessing.MinMaxScaler

2、标准化特征缩放

在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。

其中μ是平均值，σ是标准差。

python代码实现：

def preProcess(x,y):
	#标准化特征缩放
    x -= np.mean(x,axis=0)
    x /= np.std(x,axis=0,ddof=1)
    
	 #数据初始化
    x = np.c_[np.ones(len(x)),x]
    y = np.c_[y]
    return x,y
X,y = preprocess(X,y)

对应sklearn中的preprocessing.StandardScaler

3、选择缩放方法

假设我们有一个只有一个hidden layer的多层感知机（MLP）的分类问题。每个hidden unit表示一个超平面，每个超平面是一个分类边界。参数w（weight）决定超平面的方向，参数b（bias）决定超平面离原点的距离。如果b是一些小的随机参数（事实上，b确实被初始化为很小的随机参数），那么所有的超平面都几乎穿过原点。所以，如果data没有中心化在原点周围，那么这个超平面可能没有穿过这些data，也就是说，这些data都在超平面的一侧。这样的话，局部极小点（local minima）很有可能出现。 所以，在这种情况下，标准化到[-1, 1]比[0, 1]更好。

a、在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，StandardScaler表现更好。

b、在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用MinMaxScaler。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。

原因是使用MinMaxScaler，其协方差产生了倍数值的缩放，因此这种方式无法消除量纲对方差、协方差的影响，对PCA分析影响巨大；同时，由于量纲的存在，使用不同的量纲、距离的计算结果会不同。

而在StandardScaler中，新的数据由于对方差进行了归一化，这时候每个维度的量纲其实已经等价了，每个维度都服从均值为0、方差1的正态分布，在计算距离的时候，每个维度都是去量纲化的，避免了不同量纲的选取对距离计算产生的巨大影响。