目录

线性回归：

逻辑回归：

多分类问题：

全连接神经网络：

梯度：

---

线性回归：

        首先需要建立线性模型; 

        是权重向量，是自变量向量，b是偏置值。在实际问题中通过线性模型预测出的值与实际值之间会有差距，设预测值为，实际值为，则利用最小二乘法希望（-）^2尽可能小。

        定义损失函数。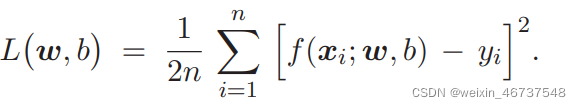

        对模型的优化实际上就是对损失函数的优化，通过不断更新和b的值来使预测直线越来越贴近实际直线。最优和b就是当损失函数取到最小值时对应的和b。具体优化过程后面会讲。主要利用梯度下降。

---

逻辑回归：

        逻辑回归虽然称为回归，但并不是解决回归问题，而是解决二分类问题。并且输出y值是0/1的二元变量。实际应用于判断一个问题是否为真，为真y就输出为1，否则输出为0.

         实际过程为：输入向量经过线性变换得到一个结果，但该结果并不符合要求的二分类输出，因此需要经过激活函数的优化。

        

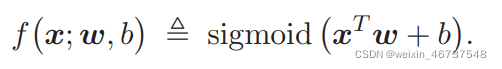
        Sigmoid就是一个激活函数，可以将输出的y值优化到一个0~1之间的数，该数称为置信率，越接近于1则表明为真的可信度越高。这样在二分类问题中就很适用。

        前面介绍的最小二乘法用于生产损失函数，在分类问题中常常利用交叉熵来产生损失函数。关于交叉熵的具体使用可以参考我之前的文章机器学习-卷积神经网络之深度残差网络CIFAR10实战（四）。交叉熵可以直接使用函数进行计算。

        同最小二乘法的损失函数的优化一样，交叉熵得到的损失函数也需要进行梯度下降不断优化和b。

---

多分类问题：

        Sigmoid函数用于二分类问题，遇到多分类问题时，考虑Softmax函数。简单介绍一下：Softmax函数使最大的元素相对变得更大，小的元素趋近于0，将每个元素对应的值转化为概率，所有元素的概率和为1，最终判断的时候直接取最大的概率对应的属性即为预测值。

        多分类问题比较基础的有对于MNIST数据集的识别，大家可以看我前面的文章机器学习-卷积神经网络MNIST实战（二）是基于卷积神经网络的。

---

全连接神经网络：

        可以看作是线性函数和激活函数相连接成为一个全连接层，单独的线性函数也可以作为一个全连接层，但一个单独的激活函数不能。多个全连接层连接就构成了全连接神经网络。每一层的输出即为下一层的输入，最后一层的输出就是全连接神经网络的输出。

---

梯度：

        在这里通俗来说就是：你求出来损失函数，对某一变量求偏导即为梯度。这些内容都可以用库函数直接实现，但前提需要读者明白怎么选择损失函数（损失函数也可以用库函数实现），对哪个变量进行优化等。

        我们力求将损失函数优化为最小，所以我们要沿着梯度下降的方向更新参数，即新参数=当前参数-学习率*当前参数的梯度。并且不断更新。随机梯度下降和梯度下降原理类似，一般选择使用随机梯度下降。都可以用库函数直接实现。