内容提要

• 线性回归的数学表达式
• 线性回归的几个概念
• 梯度下降法

一、线性回归的数学表达式

线性回归（Linear Regression）是一种通过拟合自变量xi与因变量y之间最佳线性关系，来预测目标变量的方法。所谓的线性关系就是单个xi与y两者之间的关系可用一条直线近似表示，线性回归数学表示式为：

如果上式中只包括一个自变量x和一个因变量y，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量x，且因变量y和自变量x之间是线性关系，则称为多元线性回归分析。

在线性回归解决问题中，xi称为问题的特征值，如我们研究人的身高h与营养摄入量a、锻炼强度b和睡眠时长c的关系，其中a,b,c就是特征值，也叫自变量，h是因变量，我们试图找出一个类似式1的线性函数表达式，通过该函数作为模型，在经验数据的训练下，估计出该模型的回归参数β0β1β2…，那么该模型就可以根据目标特征性[x1,x2,…,xn]预测出目标的输出值y，从而达到利用线性模型解决预测问题或计算趋势值的目的。

二、线性回归的几个概念

如前所述，回归求解过程就是用线性函数去拟合样本集，使所有样本与拟合函数之间的误差最小。如下图所示的红色圆点是一家贸易公司的广告投入与销售额之间的散点图，黑色的直线就是我们要拟合的一条直线，目标是找到一条放在合理位置的直线，所有圆点到直线的距离的平方和最小。

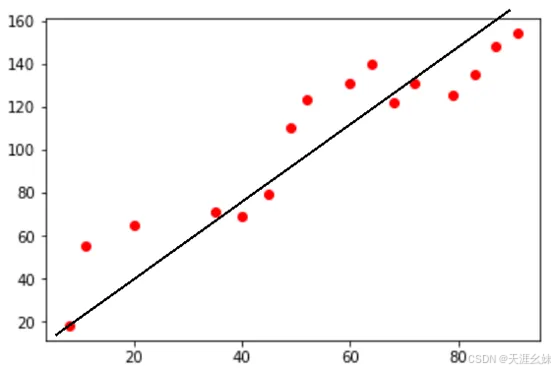
此处找直线的问题其实就是求函数y=β0+β1x中的系数β0、β1，在不断寻找（β0，β1）的过程中，必须有一种判断标准来决定何时停止迭代寻找。在线性回归中，通常使用一种称为普通最小二乘（Ordinary Least Squares,OLS）的估计方法,使得y的预测值 和真实值之间的垂直距离的平方和最小。用下式表示：

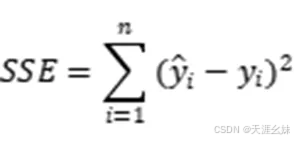
SSE表示一种总的误差，也叫损失函数，它一定程度上反应了回归方程以外因素的影响，从而导致有一定的误差，这种误差是无法避免的。此外，拟合也与样本的质量有关，试想一下，如果上张散点图的圆点本身分布波动太大，说明个别样本的变化有些偶然因素，样本的整体质量不高，从而也会导致拟合误差。样本的波动用下式表示：

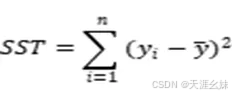
SST表示了样本中所有因变量y的实际值与其平均值

的差的平方和，其值越大，说明原始的样本数据本身具有较大的波动，反应了因变量的整体偏差。那如何评价求出的回归模型的好坏程度呢？在统计学中用下列式子来判断回归方程的拟合程度。

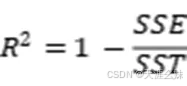
R2称为判断系数或拟合优度。由上式可知，当回归方程以外因素引起的误差SSE越小时，R2就越接近1，表示此回归方程可以很好解释因变量的变化；反之，如果SSE越大，接近总体偏差SST,那么R2就接近0，说明此问题可能不适合采用线性模型解决，因为因变量与自变量此时并不存在线性关系。

三、梯度下降法

机器学习的目标就是最小化损失函数的值，考虑最简单的情况，假设线性方程为：

y=b+wx ,则损失函数L可以理解为变量b和w的函数，记为L(b,w)，此处的b、w也可以推广为一个向量，如b=(β0),w=(β1,β2,…,βn)为自变量的各系数。因为损失函数是一个凸函数，所以寻找损失函数L(b,w)的最小值的过程，实际就是按照某种方向，不断去微调b和w的值，一步一步尝试找到这个最小值。右下图所示，一个人站在山顶的人，他试图努力花最短的距离到达谷底。显然，如果他每次都能迎着山坡最陡的方向往山坡下降的地方走，并不时地调整自己下山的步长，就能以最短的时间到达谷底。

由此可见，这个人在下到谷底的过程中，需要不断做两件事：一是始终沿最陡峭的方向下山，二是根据下降的速度来调整步长，刚开始时，可以将步长迈大些，当逐渐接近目标时，则可适当减小步长。其中，最陡峭的方向其实就是某处的梯度方向，因为梯度表示某一函数在该点处的变化率最大，对单变量的实值函数，梯度就是导数，而对于一个线性函数，梯度就是直线的斜率，步长又称为学习率 ，所以，我们把上述沿梯度方向逐步寻找损失函数最小值的方法称为梯度下降法。

损失函数最终都可以收敛到最小值或接近最小值。由上式不难看出，学习率α决定了wi变化的幅度，它决定了梯度下降的速率和稳定性，其大小需要由外界指定，不能由机器学习自身学习得来。

如果α取值太小，就像人的步长太短一样，到达谷底就要花很长时间，导致学习效率低；

如果α取值太大，虽然学习效率高，就像人的步距大一样，能很快接近谷底，但最后可能这个人一步跨过了谷底，导致始终难以到达谷底，也就是始终找不到损耗函数的最小值。

因此，通常的做法是下图所示。

步距由大到小

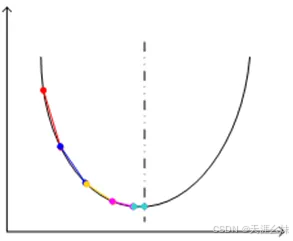
在沿着梯度方向寻找损耗函数最小值的过程中，为了平衡大小步距的优缺点，可以在一开始的时候先大步走，以提高搜寻效率，而一旦所达点的斜率逐渐下降，函数梯度下降的趋势会越来越缓，此时再逐步调小步距，以避免因步距过大而跨过谷底，从而最终找到最小值或近似最小值。

更多内容请持继关注本站！